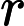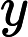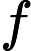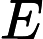[1] Brunner H.Collocation Methods for Volterra Integral and Related Functional Differential Equations. Cambridge: Cambridge University Press, 2004
[2] Roos H G, Stynes M, Tobiska L.Robust Numerical Methods for Singularly Perturbed Differential Equations: Convection-Diffusion-Reaction and Flow Problem. Berlin: Springer, 2008
[3] Ramos J I. Exponential techniques and implicit Runge-Kutta methods for singularly-perturbed Volterra integro-differential equations. Neural, Parallel & Sci Comput, 2008, 16: 387-404
[4] Amiraliyev G M, Sevgin A. Uniform difference method for singularly perturbed Volterra integro-differential equations. Appl Math Comput, 2006, 179: 731-741
[5] Cen Z D, Xi L F. A parameter robust numerical method for a singularly perturbed Volterra equation in security technologies//Processings of the 5th WSEAS Int Conference on Information Security and Privacy, Venice, Italy, 2006, November 20-22: 147-151
[6] Mbroh N A, Noutchie N C O, Masssoukou R Y M. A second order finite difference scheme for singularly perturbed Volterra integro-differential equation. Alex Eng J, 2020, 59: 2441-2447
[7] Iragi B C, Munyakazi J B. New parameter-uniform discretisations of singularly perturbed Volterra integro-differential equations. Appl Math Infor Sci, 2018, 12: 517-527
[8] Iragi B C, Munyakazi J B. A uniform convergent numerical method for a singularly perturbed Volterra integro-differential equation. Int J Comput Math, 2020, 97: 759-771
[9] Yapman Ö, Amiraliyev G M. A novel second-order fitted computational method for a singularly perturbed Volterra integro-differential equation. Int J Comput Math, 2020, 97: 1293-1302
[10] Long G Q, Liu L B, Huang Z T. Richardson extrapolation method on an adaptive grid for singularly perturbed Volterra integro-differential equations. Numer Funt Anal Opt, 2021, 42: 739-757
[11] Kauthen J P. Implicit Runge-Kutta methods for some integrodifferential-algebraic equations. Appl Numer Math, 1993, 13: 125-134
[12] Horvat V, Rogina M. Tension spline collocation methods for singularly perturbed Volterra integro-differential and Volterra integral equations. Comput Appl Math, 2002, 140: 381-402
[13] Tao X, Zhang Y H. The coupled method for singularly perturbed Volterra integro-differential equations. Adv Differ Equ, 2019, 2019: 1-16
[14] Reed W H, Hill T R.Triangular mesh methods for neutron transport equation. Technical Report LA-UR-73-479, Los Alamos Scientific Laboratory, Los Alamos, 1973
[15] Cockburn B, Shu C W. The local discontinuous Galerkin method for time-dependent convection-diffusion systems. SIAM J Numer Anal, 1998, 35: 2440-2463
[16] Celiker F, Cockburn B. Superconvergence of the numerical traces of discontinous Galerkin and hybridized methods for convection-diffusion problems in one space dimension. Math Comput, 2007, 76: 67-96
[17] Xie Z Q, Zhang Z. Superconvergence of DG method for one-dimensional singularly perturbed problems. J Comput Math, 2007, 25: 185-200
[18] Xie Z Q, Zhang Z. Uniform superconvergence analysis of the discontinuous Galerkin method for a singularly perturbed problem in 1-D. Math Comput, 2010, 79: 35-45
[19] Zeng Z K, Chen Y P. A local discontinuous Galerkin method for fractional diffusion equations. Acta Mathematica Scientia, 2023, 43B(2): 839-854
[20] Larsson S, Thomée V, Wahlbin L B. Numerical solution of parabolic integro-differential equations by the discontinuos Galerkin method. Math Comput, 1998, 87: 45-71
[21] Brunner H, Schötzau D.   -Discontinous Galerkin time-stepping for Volterra integrodifferential equations. SIAM J Numer Anal, 2006, 44: 224-245 -Discontinous Galerkin time-stepping for Volterra integrodifferential equations. SIAM J Numer Anal, 2006, 44: 224-245
[22] Chen C M, Shih T.Finite Element Methods for Integrodifferential Equations. Singapore: World Scientific, 1998
[23] Kauthen J P. A survey of singularly perturbed Volterra equations. Appl Numer Math, 1997, 24: 95-114
[24] Angell J S, Olmstead W E. Singularly perturbed Volterra integral equations. SIAM J Numer Math, 1987, 47(1): 1-14
[25] Angell J S, Olmstead W E. Singularly perturbed Volterra integral equations II. SIAM J Numer Math, 1987, 47(6): 1150-1162
[26] Bijura A M. Rigorous results on the asymptotic solutions of singularly perturbed nonlinear Volterra integral equations. J Integral Equ Appl, 2002, 14(2): 119-149
[27] Bijura A M. Asymptotics of integrodifferential models with integrable kernels. Int J Math Math Sci, 2003, 2003(25): 1577-1598
[28] Jordan G S. A nonlinear singularly perturbed Volterra integrodifferential equation of nonconvolution type. Proc Roy Soc Edinburgh Sect A, 1978, 80: 235-247
[29] Jordan G S.Some nonlinear singularly perturbed Volterra integro-differential equations//Londen S, Staffans O. Volterra Equations. Berlin: Springer, 1979: 107-119
[30] Lodge A S, Mcleod J B, Nohel J E. A nonlinear singularly perturbed Volterra integrodifferential equation occuring in polymer rheology. Proc Roy Soc Edinburgh Sect A, 1978, 80: 99-137
[31] Mustapha K, Mclean W. Discontinuous Galerkin method for an evolution equation with a memory term of positive type. Math Comput, 2009, 78(268): 1975-1995 |