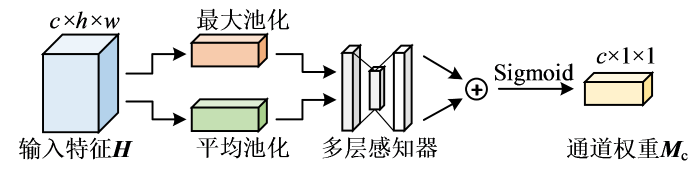波谱学杂志, 2023, 40(3): 307-319 doi: 10.11938/cjmr20223040

研究论文

融合注意力机制的多尺度残差Unet的磁共振图像重建

李奕洁, 杨馨雨, 杨晓梅,*

四川大学 电气工程学院，四川 成都 610065

Magnetic Resonance Image Reconstruction of Multi-scale Residual Unet Fused with Attention Mechanism

Li Yijie, YANG Xinyu, YANG Xiaomei,*

College of Electrical Engineering, Sichuan University, Chengdu 610065, China

通讯作者: *Tel: 13708045831, E-mail:yangxiaomei@scu.edu.cn.

收稿日期: 2022-11-25   网络出版日期: 2023-01-29

Corresponding authors: *Tel: 13708045831, E-mail:yangxiaomei@scu.edu.cn.

Received: 2022-11-25   Online: 2023-01-29

摘要

为了提高磁共振图像在欠采样下重建的质量，本文融合注意力机制和多尺度残差卷积构建Unet网络，实现磁共振图像在欠采样下的重建算法．为增强网络特征的表现能力，以及防止网络训练中梯度消失与退化的问题，在Unet网络的编码路径中引入多尺度残差卷积，提取不同尺度的特征信息；为能准确地恢复图像的细节纹理特征，在Unet网络编码和解码路径的跳层拼接部分引入卷积注意力块，对细节纹理等关键信息进行不同程度的响应．实验表明，本文方法可通过欠采样k-空间数据快速重建出细节纹理清晰且无重叠伪影的高质量磁共振图像．

关键词： 磁共振成像; 图像重建; Unet; 注意力机制; 深度学习

Abstract

This paper integrates the attention mechanism and multi-scale residual convolution to construct a Unet network, aiming at improving the quality of magnetic resonance image (MRI) reconstructed from under-sampled k-space data. To enhance the feature representation ability of the network and prevent gradient disappearance and degradation during network training, multi-scale residual convolution was embedded in the encoding path of the Unet network to extract different scale feature information of MRI. Moreover, to accurately recover the detailed texture features of MRI, the convolution attention module was embedded in the jump connection part between the encoding and decoding path of the Unet network to respond to the key information, such as details and textures in different degrees. Experiments showed that the proposed network could effectively reconstruct high-quality MRIs with clear texture and without overlapping artifacts from the under-sampled k-space data.

Keywords： magnetic resonance imaging; image reconstruction; Unet; attention mechanism; deep learning

PDF (1047KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

李奕洁, 杨馨雨, 杨晓梅. 融合注意力机制的多尺度残差Unet的磁共振图像重建[J]. 波谱学杂志, 2023, 40(3): 307-319 doi:10.11938/cjmr20223040

Li Yijie, YANG Xinyu, YANG Xiaomei. Magnetic Resonance Image Reconstruction of Multi-scale Residual Unet Fused with Attention Mechanism[J]. Chinese Journal of Magnetic Resonance, 2023, 40(3): 307-319 doi:10.11938/cjmr20223040

引言

磁共振成像（magnetic resonance imaging，MRI）是一种广泛应用于临床的医学成像方式[1]，但存在k-空间数据采集时间过长的缺陷.导致磁共振图像可能因患者的运动和生理运动（如心脏搏动、呼吸活动和胃肠道蠕动）而出现明显的伪影.

压缩感知（compressed sensing，CS）[2]-MRI技术能以低于奈奎斯特采样率的频率对k-空间数据进行欠采样，从而加快成像速度.针对CS-MRI的图像重建方法利用了磁共振图像的稀疏性构建重建模型，通过非线性优化或迭代算法实现图像的重建[3].常用的稀疏变换有全变分（total variation，TV）[4,5]、离散余弦变换[6]、小波变换[7⇓-9]和字典学习[10,11]等.此外，也有学者们融合磁共振图像的稀疏性和低秩性构建CS-MRI重建模型[12,13].但由于一般的稀疏或低秩变换难以精确捕捉组织器官的复杂细节纹理，且非线性优化求解通常涉及多次迭代计算，导致重建时间相对较长，而且不适当的超参数设置将产生过度平滑或不自然的重建图像，因而获得较为满意的CS-MRI重建图像还存在一定困难.

随着深度学习的高速发展，许多基于深度学习的算法已经广泛应用于基于CS-MRI的图像重建中[14⇓-16].目前，深度学习框架下的磁共振图像重建大致采用“端到端映射”（end-to-end mapping）和“基于模型展开”（model-based unrolling）两类方法.“端到端映射”方法直接借助各种不同的深度网络（如结构简单的全卷积神经网络Unet[17]、多尺度残差网络[18]、生成对抗网络[19]等），利用海量数据离线学习“含伪影噪声的欠采样图像”和“参考图像”之间、“欠采样k-空间数据”和“全采样k-空间数据”之间的非线性映射关系，得到参数优化的重建网络.“基于模型展开”的方法则将基于CS-MRI模型的迭代求解展开为深度神经网络计算，如ADMM-Net[20]、ISTA-Net[21]和IFR-Net[22]等，每一个迭代步骤对应于一个神经网络模块，迭代次数对应于网络层数，模型的正则化参数和各种稀疏变换等超参数则成为网络的参数，使得深度网络具有可解释性.这些开创性的工作显示了深度学习在基于CS-MRI的图像重建方面的巨大潜力.

鉴于Unet网络具有使用小样本数据集也能够取得很好的网络模型训练效果的优势，本文以Unet网络为框架，并做出如下改进：(1)将多尺度残差模块（multi-scale residual convolution module，MRCM）引入Unet网络的编码结构中，这样能够更加充分地提取图像的特征信息，并且有利于网络训练时梯度的反向传播；(2)在网络的跳层拼接部分使用卷积块注意模块（convolutional block attention module，CBAM），增强模型对细节纹理的关注并且抑制伪影噪声，提出了一种基于注意力机制的多尺度残差U型网络模型（attention multi-scale residual Unet，AttMRes-Unet）.本文提出的网络模型很好地恢复了图像细节，减少了重建图像中的混叠伪影，提高了重建图像的质量.

1 理论部分

1.1 基于CS-MRI的图像重建模型

CS理论通过欠采样k-空间数据缩短数据采集时间，其欠采样模型可以表示为：

$y={{F}_{\Omega }}x+\varepsilon $

其中$y\in {{C}^{m}}$，为欠采样后的k-空间数据；$x\in {{R}^{n}}$$(m\le n)$，为待恢复的磁共振图像；${{F}_{\Omega }}\in {{C}^{m\times n}}$，代表傅里叶欠采样算子；ε代表噪声.C为复数域，R为实数域，m与n代表不同的维度.

传统的CS-MRI重建方法利用磁共振图像的稀疏性或低秩性等先验信息，通过非线性优化求解如(2)式所示的重建模型，从y中重建出图像x：

$\underset{x}{\mathop{\min }}\,\left\{ \frac{1}{2}\left\| y-{{F}_{\Omega }}x \right\|_{2}^{2}+{{\lambda }_{1}}\varphi (x) \right\}$

其中，$\varphi (x)$为图像的稀疏性或低秩性表示函数，可利用TV、小波变换或奇异值分解加以实现；${{\lambda }_{1}}$为拉格朗日系数，权衡保真项$\frac{1}{2}\left\| y-{{F}_{\Omega }}x \right\|_{2}^{2}$和稀疏（或低秩）信息间的权重.

端对端的深度学习模型则是通过构建深度神经网络模型建立y与x之间的非线性函数，从而实现图像x的重建.

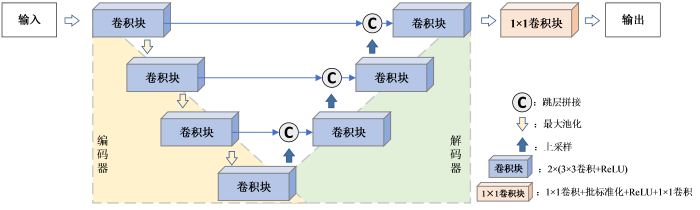
1.2 基于Unet网络的MRI重建

Unet网络最初被应用于图像分割领域，并且表现卓越[23,24].随着研究的深入，Unet也逐渐应用于图像重建[25,26].其网络结构如图1所示，主要由编码器和解码器两部分构成.编码器通过卷积和池化学习提取输入图像的语义信息，并将特征映射至更高维度.解码器通过对特征图像进行上采样操作不断恢复特征图的分辨率.通过引入与编码器对应层相接的跳层拼接，实现浅层与深层特征的融合，协助解码器完成特征重建.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   Unet网络结构

Fig. 1   The architecture of Unet


然而对于细节特征丰富的磁共振图像，编码器中的普通卷积不能很好地提取图像的纹理信息，并且浅层特征与深层特征存在着较大的语义差异[27]，直接使用跳层拼接可能会使重建图像存在较多的伪影与噪声.因此，本文在Unet网络的架构基础上进行了改进，以便提升网络重建磁共振图像的性能.

1.3 基于注意力机制的多尺度残差Unet网络

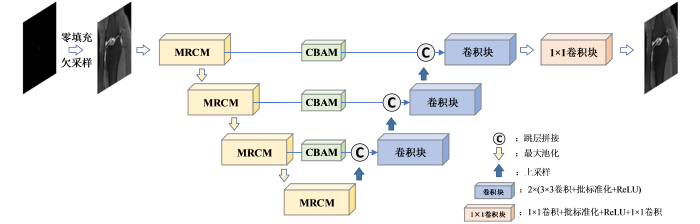
本文提出的基于AttMRes-Unet网络的重建模型如图2所示，对数据集中欠采样的k-空间数据进行零填充后得到零填充图像，输入至AttMRes-Unet网络得到相应的重建图像.在编码器部分，引入残差机制，在实现深度提取特征的同时避免网络退化和梯度消失；并引入多尺度卷积的策略，将残差学习由单一路径卷积扩展成多路径多尺度卷积，增加网络宽度，丰富网络的特征提取能力，从而构建出MRCM；在解码器部分，为了能更好地恢复图像的纹理细节，在跳层拼接部分引入CBAM注意力模块，对编码器得到的各层次特征依据其重要性实现不同程度的加权，加强网络模型对图像细节特征的学习，提高重建图像的质量.如图2中所示，在编码器部分包含4个MRCM，在跳层拼接部分采用了3个CBAM.输入图像第一次经过MRCM运算后通道数从1升至16，之后每经过一次MRCM运算，特征图的通道数加倍，即4个MRCM的输出通道分别为16、32、64、128.与经典Unet网络的最大池化保持一致，使用池化核大小为2×2、步长为2的最大池化操作提取最显著特征并实现特征图大小的减半，从而将特征图由从扁平状转换为小而密的立体图；在解码部分，各层均采用最邻近插值法将特征图大小加倍，并通过3×3的卷积运算使特征图通道数减半，从而实现上采样操作；为避免上采样造成的特征信息损失，将上采样之后的特征图与来自于编码器的CBAM加权后的特征图进行跳层拼接.经过3次上采样操作以后，特征图最终恢复到与输入图像相同的大小.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   基于AttMRes-Unet网络的重建模型

Fig. 2   Reconstruction model based on AttMRes-Unet network


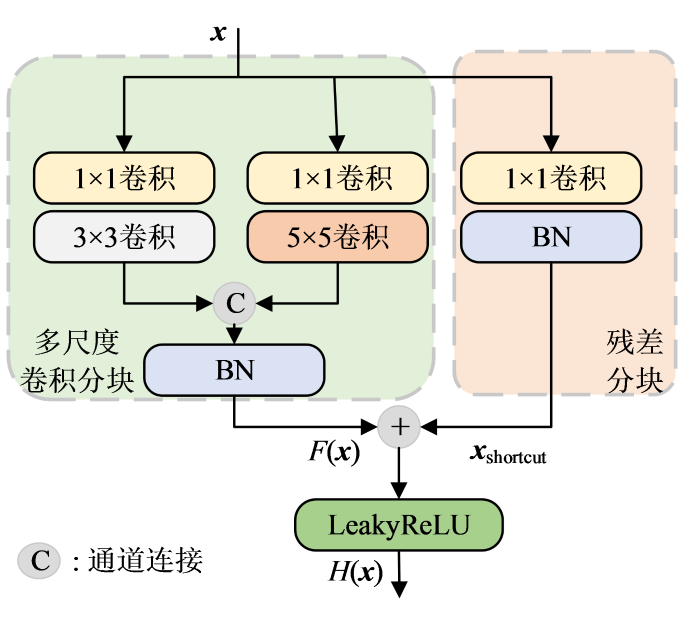
1.3.1 MRCM

MRCM的结构如图3所示.对于当前模块的输入x，在多尺度卷积分块中，首先通过步长为1，无填充的1×1卷积，然后再通过包含3×3与5×5的两个卷积分支的运算提取出不同感受野的特征，得到尺寸大小相同的特征图.其中，使用3×3卷积学习相应的细节纹理信息，卷积核的步长为1，填充为1；而具有5×5大小感受野的卷积核更适合提取结构特征信息，其步长为1，填充为2.填充方式均选择零填充.为有效地利用不同尺度的特征信息，执行特征通道上的拼接，经批标准化（batch normalization，BN）运算后得到特征输出$F(x)$.在实际的临床应用中，不同人体组织对应的磁共振图像包含的重要特征部分尺寸大小不同，与单尺度的卷积相比，多尺度卷积在不增加网络深度和不占用大量计算资源的同时使用不同尺寸的卷积核提取不同尺度的特征，兼顾了细节与结构特征的提取与学习，更利于图像的重建.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   多尺度残差模块（MRCM）

Fig. 3   Multi-scale residual convolution module (MRCM)


为缓解网络训练中可能出现的梯度消失和网络退化问题，引入了残差机制[29].不同于一般的残差机制直接将模块的输入x与多尺度卷积块输出$F(x)$进行叠加，在MRCM中，输入x通过多尺度卷积后，$F(x)$的通道数多于输入x的通道数，因此x需要通过1×1卷积进行升维.例如，通道数为1的欠采样图像x在第一层多尺度残差模块时，经过多尺度卷积分块后的特征图$F(x)$通道变为16，为了能实现x与$F(x)$的叠加，需要将x经过1×1×1×16卷积后将通道数升至16，如图3中的残差分块所示.

考虑到LeakyReLU函数在特征值为负数时对其赋予很小的斜率，解决了ReLU函数存在的“神经坏死”问题，更有利于网络训练.因此本文在MRCM中使用LeakyReLU函数作为激活函数，其负半轴斜率为0.001，由此得到多尺度残差块的输出$H(x)$，可表示为：

$H(x)=\operatorname{LeakyReLU}(F(x)+{{x}_{shortcut}})$

其中，${{x}_{shortcut}}$表示输入x经过残差分块后得到的输出.

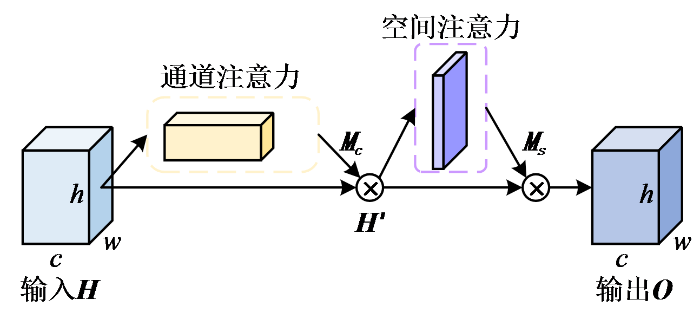
1.3.2 CBAM

通过解码器得到的浅层特征包含较多图像的细粒度信息（如纹理、边缘等），随着网络层数的加深，解码器提取到的更多是抽象的语义信息而忽略了细节信息.为防止重要细节纹理信息的丢失，本文在跳层拼接部分引入融合通道注意力机制与空间注意力机制的CBAM，以强调细节信息，并去除冗杂的信息，从而使解码器充分利用浅层特征从而提高重建精度.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   卷积块注意模块（CBAM）

Fig. 4   Convolutional block attention module (CBAM)


CBAM在通道与空间两个维度上依次生成注意力图，并将相对应的输入与注意特征图加权之后得到输出，表达式如(4)式和(5)式所示：

${H}'={{M}_{\text{c}}}(H)\otimes H$
$O={{M}_{\text{s}}}({H}')\otimes {H}'$

其中H为输入特征，${{M}_{\text{c}}}$为通道模块权重，${{H}^{\prime }}$为H与${{M}_{\text{c}}}$加权后所得的特征图，${{M}_{\text{s}}}$为空间模块权重，O为输出特征，$\otimes $表示对应元素依次相乘.

通道注意力机制对特征图的每个通道的重要性进行判断，并对其进行权重分配，权重越大表示该通道的特征越重要，其结构如图5所示.图中，⊕表示按位相加.通道注意力分别通过全局最大池化与全局平均池化对输入特征H的空间维度进行压缩，然后通过具有一层隐藏层的多层感知器（multilayer perceptron，MLP）进行映射，最后再经过Sigmoid函数得到相应的通道权重，表达式为：

${{M}_{\text{c}}}(H)=Sigmoid(\operatorname{MLP}(\operatorname{MaxPool}(H))+\operatorname{MLP}(\operatorname{AvgPool}(H)))$

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   通道注意力机制

Fig. 5   Channel attention mechanism


其中，MaxPool(∙)为池化核大小与步长都为2的最大池化，AvgPool(∙)为池化核大小与步长都为2的平均池化，MLP(∙)为多层感知器.

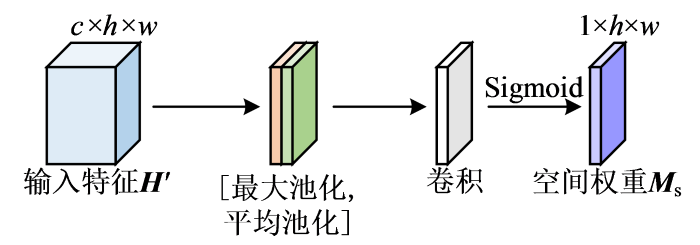
空间注意力机制对特征图中值得注意的位置信息进行关注.如图6所示，空间注意力对输入特征${{H}^{\prime }}$先后执行全局平均池化与全局最大池化，然后对通道拼接后的特征图进行7×7的卷积，最后经过Sigmoid函数激活获得归一化的空间权重${{M}_{\text{s}}}$，表达式为：

${{M}_{\text{s}}}({H}')=Sigmoid({{\operatorname{conv}}^{7\times 7}}(\operatorname{concat}(\operatorname{MaxPool}({H}');\operatorname{AvgPool}({H}'))))$

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   空间注意力机制

Fig. 6   Spatial attention mechanism


其中，$\text{concat}(\cdot )$为通道拼接，${{\operatorname{conv}}^{7\times 7}}(\cdot )$为7×7卷积.

1.3.3 损失函数

本文使用平均绝对值误差（mean absolute error，MAE）作为损失函数，公式如式(8)所示：

$\text{Loss}=\frac{1}{n}\sum\nolimits_{i=1}^{n}{\left| {{y}_{i}}-{{{\hat{y}}}_{i}} \right|}$

其中，y代表真实的磁共振图像，$\hat{y}$代表相应的重建图像，n代表每轮训练迭代时的图像数量.

3 实验部分

3.1 数据集

本文使用公开的fastMRI数据集[30] 的单线圈采集的人体膝盖的k-空间数据与对应的全采样图像进行实验.该数据集包含了973个卷作为训练集（共41 877个切片），199个卷作为验证集（共7 135个切片）.该数据集原始k-空间数据序列大小为640×372，考虑到实际应用中，笛卡尔采样所需硬件条件较低，采样轨迹容易实现且快速灵活[32]，因此本文使用笛卡尔采样（图7），在一定的加速因子下完成k-空间数据的欠采样.加速因子与欠采样率成反比，如当加速因子为4时，欠采样率为1/4=25%.将欠采样的k-空间数据进行零填充并执行傅里叶反变换得到磁共振图像，并以中心裁剪的方式获得统一的320×320像素图像作为网络输入，进行图像重建.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   笛卡尔采样模板

Fig. 7   Cartesian mask


3.2 实验参数设置

本文实验的硬件配置使用NVIDIA GeForce RTX 3060 GPU（12 GB显存）的Windows操作系统，编程语言为Python，所有实验均在Tensorflow框架的keras平台环境下进行.网络选择Adam优化器更新网络参数，其指数衰减率参数默认为β1=0.9与β2=0.999，设置初始学习率为0.001，网络迭代次数为100.

3.3 评价指标

为了定量评价算法的重建效果，本文采用峰值信噪比（peak signal-to-noise ratio，PSNR）、结构相似性（structure similarity index measurement，SSIM）作为评价指标.其中，PSNR反映重建图像与全采样图像的一致性，SSIM用于评价重建图像与全采样图像之间的相似程度，计算方式如(9)式和(10)式所示：

$\operatorname{PSNR}(x,\hat{x})=10\lg (\frac{\max {{(x)}^{2}}}{\frac{1}{n}\sum\nolimits_{i,j}{{{({{x}_{i,j}}-{{{\hat{x}}}_{i,j}})}^{2}}}})$
$\operatorname{SSIM}(x,\hat{x})=\frac{(2{{\mu }_{x}}{{\mu }_{{\hat{x}}}}+{{c}_{1}})(2{{\sigma }_{x}}{{\sigma }_{{\hat{x}}}}+{{c}_{2}})({{\operatorname{cov}}_{x}}_{{\hat{x}}}+{{c}_{3}})}{({{\mu }_{x}}^{2}+{{\mu }_{{\hat{x}}}}^{2}+{{c}_{1}})({{\sigma }_{x}}^{2}+{{\sigma }_{{\hat{x}}}}^{2}+{{c}_{2}})({{\sigma }_{x}}{{\sigma }_{{\hat{x}}}}+{{c}_{3}})}$

其中，x代表全采样图像，$\hat{x}$代表重建图像，$\max (x)$代表图像的最大像素值，μ代表图像像素的均值，σ代表图像的像素方差，cov代表两图像素协方差，${{c}_{i}}$为常数，${{c}_{1}}={{({{k}_{1}}L)}^{2}}$，${{c}_{2}}={{({{k}_{2}}L)}^{2}}$，${{c}_{3}}={{c}_{2}}/2$，根据经验常取${{k}_{1}}=0.01$，${{k}_{2}}=0.03$，L为图像像素值的动态范围.

同时使用网络参数量、网络训练时间与单个切片的重建时间对网络模型进行评价.

4 结果与讨论

4.1 网络模型对比

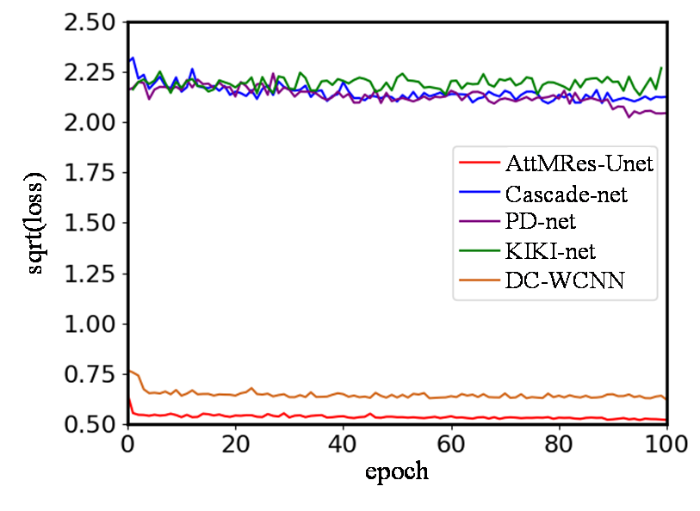
为验证本文算法的优越性，将提出的AttMRes-Unet与基于深度学习的CS-MRI重建算法中流行的算法PD-net[31]、Cascade-net[32]、KIKI-net[33]、DC-WCNN[34]进行对比.其中，前三个网络的参数设置与原文献一致；而DC-WCNN的基础网络框架也为Unet网络，因此其网络层数和各层输出通道数设置与AttMRes-Unet一致.

首先，对各个网络在训练集上的损失值变化进行比较.为了呈现良好的对比效果，以网络损失值的均方根值为纵坐标，迭代次数为横坐标，绘制网络训练的收敛曲线.以加速因子为4为例，5个网络训练的收敛曲线如图8所示，加速因子为2和3时的收敛曲线如图S1和S2所示.可以看出，AttMRes-Unet网络的损失收敛最快，在相同学习率下损失减少的最多，说明网络的拟合效果最好.DC-WCNN网络也能较好的收敛，但是得到的损失值高于AttMRes-Unet网络.其余3个网络的损失值较大，可解释为迭代次数较少，网络对本训练集不能呈现较好的拟合效果.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   加速因子为4时各个网络在训练集上的收敛曲线

Fig. 8   Convergence curves of each network on the training set when the acceleration factor is 4


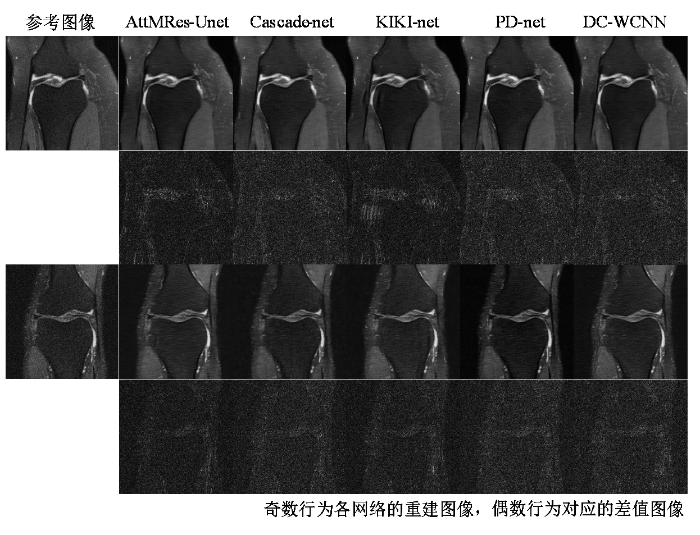
当加速因子为2、3、4时，5种网络在验证集上的平均PSNR和SSIM如表1所列.各个模型的网络参数量、训练时间与单个切片的重建时间如表2所示.KIKI-net参数量最大，重建的各项指标均为最低，其原因在于过多的级联导致了网络的过拟合.PD-net的参数量远少于AttMRes-Unet网络，但PD-net需要在k-空间与图像域中交替更新，导致网络训练的时间最长，重建时间超过AttMRes-Unet的23倍.Cascade-net参数量较小，训练时间和重建时间较少，重建质量略优于KIKI-net，但仍低于PD-net、DC-WCNN与AttMRes-Unet. DC-WCNN的网络参数量、训练时间与重建时间均高于AttMRes-Unet，而图像的重建质量均略低于AttMRes-Unet网络.总的来说，AttMRes-Unet在重建质量（在不同加速因子下重建得到的图像都具有更高的PSNR与SSIM）、训练时间与重建时间上相较于其他四个网络具有明显的优势，体现了良好的应用性能.选取不同样本的两张膝盖全采样图像作为参考图像，5种网络模型在加速因子为4下得到的重建图像与相应误差图像如图9所示，加速因子为2、3下得到的重建图像与相应误差图像如图S3和S4所示.相比于其他模型，AttMRes-Unet网络的重建图像细节纹理特征最为清晰，对应差值图像像素分布均匀，轮廓最模糊.

表1   5种网络模型重建图像的平均性能

Table 1  Average performance of reconstructed images by five network models

网络模型PSNRSSIM
×2×3×4×2×3×4
PD-net32.5438±1.098130.9821±1.123030.6958±1.09230.7736±0.08120.6802±0.08000.6345±0.0813
Cascade-net31.5583±1.112030.1253±1.09629.8148±1.02200.7651±0.07950.6752±0.08200.6340±0.0760
KIKI-net30.7728±1.459228.6321±1.320129.7129±1.53290.7532±0.08210.6457±0.08320.6274±0.0846
DC-WCNN32.8576±1.078630.9972±1.235630.7214±1.06430.7821±0.08310.6853±0.08010.6399±0.0842
AttMRes-Unet33.2185±1.275931.7255±1.179430.9175±1.23760.7862±0.08620.6972±0.08590.6497±0.0865

新窗口打开| 下载CSV


表2   5种网络模型的网络参数、训练时间与重建时间对比

Table 2  Comparison of network parameters, training time and reconstruction time of five network models

网络模型参数量训练时间/s重建时间/ms
PD-net3182809024487.5
Cascade-net424570359770.1
KIKI-net8905046302186.8
DC-WCNN534080480932.9
AttMRes-Unet404714230121.1

新窗口打开| 下载CSV


图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   加速因子为4时的对比实验重建效果对比

Fig. 9   Reconstruction results of different networks in comparative experiments when the acceleration factor is 4


4.2 消融实验

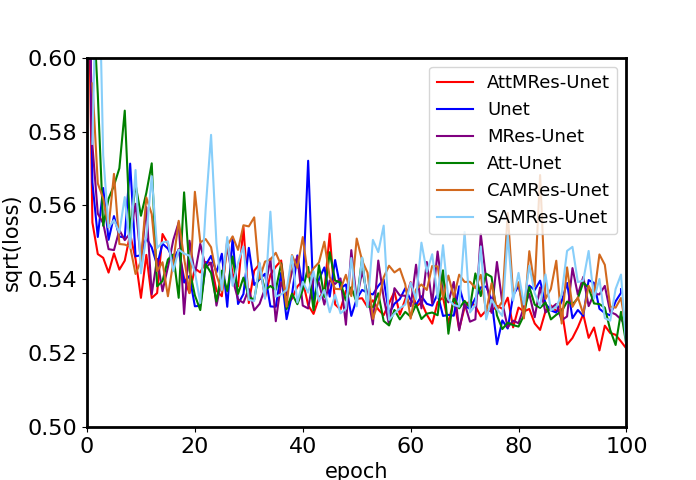
为了分析验证本文在Unet网络架构中引入的各个模块对磁共振图像重建质量提升的有效性，分别使用Unet、仅有MRCM模块的MRes-Unet、仅有CBAM块的Att-Unet、包含通道注意力与MRCM模块的CAMRes-Unet、包含空间注意力与MRCM模块的SAMRes-Unet，与本文所提出的AttMRes-Unet网络进行消融实验.加速因子为4时，6个网络在训练集上的收敛曲线如图10所示；加速因子为2、3时，6个网络在训练集上的收敛曲线如图S5、S6所示.其中，AttMRes-Unet网络的损失曲线收敛最快并稳定下降.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   加速因子为4时消融实验收敛曲线

Fig. 10   Convergence curves of ablation experiments when the acceleration factor is 4


表3列出了不同加速因子下各种网络的平均性能，从表中看出，Att-Unet、MRes-Unet、CAMRes-Unet、SAMRes-Unet与AttMRes-Unet的大部分指标均高于Unet.在MRes-Unet网络的基础上再单独增加通道注意力或空间注意力机制均提升了重建图像的质量.在所有网络中，AttMRes-Unet网络重建图像具有最高的PSNR与SSIM.由此可以得出，在Unet基础网络中增加MRCM模块与CBAM块都能有效地提高重建精度.加速因子为4时，各个网络对两个不同样本的膝盖图像的重建可视化效果如图11所示，加速因子为2、3时，各个网络对两个不同样本的膝盖图像的重建可视化效果如图S7、S8所示.AttMRes-Unet网络的重建图像视觉效果更加清晰，细节方面恢复的更好，对应的差值图中轮廓最模糊，与参考图像的差异最小.

表3   消融实验网络模型的平均性能

Table 3  Average performance of networks in ablation experiments

网络模型PSNRSSIM
×2×3×4×2×3×4
Unet32.5193±1.090131.3347±1.089930.8267±1.09210.7771±0.07610.6829±0.07700.6475±0.0769
Att-Unet32.9367±1.109631.5930±1.201930.9052±1.10990.7777±0.07990.6887±0.08110.6485±0.0787
MRes-Unet33.0847±0.999831.6665±1.062130.9085±1.22600.7849±0.08140.6959±0.08160.6445±0.0813
SAMRes-Unet33.1018±1.392131.6770±1.299830.9095±1.29750.7852±0.08240.6953±0.08270.6466±0.0825
CAMRes-Unet33.1115±1.300131.6801±1.264530.9106±1.23010.7856±0.08310.6960±0.08290.6476±0.0833
AttMRes-Unet33.2185±1.275931.7255±1.179430.9175±1.23760.7862±0.08620.6972±0.08590.6497±0.0865

新窗口打开| 下载CSV


图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   加速因子为4时的消融实验重建效果对比

Fig. 11   Reconstruction results of different networks in ablation experiments when the acceleration factor is 4


各个网络的网络参数量、训练时间与重建时间如表4所列，相较于Unet，Att-Unet中增加的CBAM模块带来了网络参数的少量增长，因此网络的训练时间与重建时间略长于Unet；而MRes-Unet、SAMRes-Unet、CAMRes-Unet与AttMRes-Unet中MRCM模块的1×1卷积则大量减少了网络参数，因此各个网络的训练时间均少于Unet网络，但重建时间均长于Unet.

表4   消融实验网络模型的参数量、训练时间与重建时间

Table 4  Network parameters, training time and reconstruction time in ablation experiments

网络模型参数量训练时间/s重建时间/ms
Unet485065249819.4
Att-Unet490730250620.6
MRes-Unet399049224019.9
SAMRes-Unet399058225320.1
CAMRes-Unet404705228920.2
AttMRes-Unet404714230121.1

新窗口打开| 下载CSV


5 结论

本文提出了一种融合注意力机制的多尺度残差Unet网络的磁共振图像重建算法，该算法以Unet为基础网络架构，在编码部分引入多尺度残差模块代替普通卷积，防止网络梯度消失的同时增强特征提取能力；在跳层拼接部分使用了CBAM块，使得图像的有用信息得到充分的强调，恢复图像细节的同时减少了混叠伪影.实验结果表明，在磁共振图像重建上，AttMRes-Unet网络模型具有不错的性能，重建出的图像细节纹理清晰，并且所消耗的时间远低于其他算法，具有实用性.

利益冲突

无

附件材料（可在《波谱学杂志》官网 http://magres.wipm.ac.cn浏览该论文网页版获取）

图S1 加速因子为2时各个网络在训练集上的收敛曲线

图S2 加速因子为3时各个网络在训练集上的收敛曲线

图S3 加速因子为2时对比实验重建效果对比

图S4 加速因子为3时对比实验重建效果对比

图S5 加速因子为2时消融实验收敛曲线

图S6 加速因子为3时消融实验收敛曲线

图S7 加速因子为2时消融实验重建效果对比

图S8 加速因子为3时消融实验重建效果对比

参考文献

LIU Y Y, YANG Y X, ZHU Q Y, et al.

Accelerating T1ρ dispersion imaging with multiple relaxation signal compensation

[J]. Chinese J Magn Reson, 2022, 39(3): 243-257.

[本文引用: 1]

刘元元, 杨育昕, 朱庆永, 等.

基于多弛豫信号补偿的快速磁共振T1ρ散布成像

[J]. 波谱学杂志, 2022, 39(3): 243-257.

[本文引用: 1]

DONOHO D L.

Compressed sensing

[J]. IEEE Trans Inform Theory, 2006, 52(4): 1289-1306.

DOI:10.1109/TIT.2006.871582      URL     [本文引用: 1]

刘晓晖. 基于压缩感知的磁共振图像稀疏重建算法研究[D]. 广州: 南方医科大学, 2018.

[本文引用: 1]

MICHAEL L, DONOHO D L, PAULY J M.

Sparse MRI: the application of compressed sensing for rapid MR imaging

[J]. Magn Reson Med, 2007, 58(6): 1182-1195.

DOI:10.1002/mrm.21391      PMID:17969013      [本文引用: 1]

The sparsity which is implicit in MR images is exploited to significantly undersample k-space. Some MR images such as angiograms are already sparse in the pixel representation; other, more complicated images have a sparse representation in some transform domain-for example, in terms of spatial finite-differences or their wavelet coefficients. According to the recently developed mathematical theory of compressed-sensing, images with a sparse representation can be recovered from randomly undersampled k-space data, provided an appropriate nonlinear recovery scheme is used. Intuitively, artifacts due to random undersampling add as noise-like interference. In the sparse transform domain the significant coefficients stand out above the interference. A nonlinear thresholding scheme can recover the sparse coefficients, effectively recovering the image itself. In this article, practical incoherent undersampling schemes are developed and analyzed by means of their aliasing interference. Incoherence is introduced by pseudo-random variable-density undersampling of phase-encodes. The reconstruction is performed by minimizing the l(1) norm of a transformed image, subject to data fidelity constraints. Examples demonstrate improved spatial resolution and accelerated acquisition for multislice fast spin-echo brain imaging and 3D contrast enhanced angiography.(c) 2007 Wiley-Liss, Inc.

GOPI V P, PALANISAMY P, WAHID K A, et al.

Multiple regularization based MRI reconstruction

[J]. Signal Process, 2014, 103: 103-113.

DOI:10.1016/j.sigpro.2013.11.001      URL     [本文引用: 1]

YU Y, HONG M, LIU F, et al.

Compressed sensing MRI using singular value decomposition based sparsity basis

[C]// Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Boston, USA, IEEE, 2011: 5734-5737.

[本文引用: 1]

HUANG J, ZHANG S, METAXAS D.

Efficient MR image reconstruction for compressed MR imaging

[J]. Med Image Anal, 2011, 15: 670-679.

DOI:10.1016/j.media.2011.06.001      PMID:21742542      [本文引用: 1]

In this paper, we propose an efficient algorithm for MR image reconstruction. The algorithm minimizes a linear combination of three terms corresponding to a least square data fitting, total variation (TV) and L1 norm regularization. This has been shown to be very powerful for the MR image reconstruction. First, we decompose the original problem into L1 and TV norm regularization subproblems respectively. Then, these two subproblems are efficiently solved by existing techniques. Finally, the reconstructed image is obtained from the weighted average of solutions from two subproblems in an iterative framework. We compare the proposed algorithm with previous methods in term of the reconstruction accuracy and computation complexity. Numerous experiments demonstrate the superior performance of the proposed algorithm for compressed MR image reconstruction.Copyright © 2011 Elsevier B.V. All rights reserved.

MA S, YIN W, ZHANG Y.

An efficient algorithm for compressed MR imaging using total variation and wavelets

[C]// IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA: IEEE, 2008: 1-8.

[本文引用: 1]

CHEN Z, FU Y, XIANG Y, et al.

A novel low-rank model for MRI using theredundant wavelet tight frame

[J]. Neurocomputing, 2018: S0925231218301310.

[本文引用: 1]

RAVISHANKAR S, BRESLER Y.

MR image reconstruction from highly undersampled k-space data by dictionary learning

[J]. IEEE T Med Imaging, 2010, 30(5): 1028-1041.

DOI:10.1109/TMI.2010.2090538      URL     [本文引用: 1]

IKRAM S, ZUBAIR S, SHAH J A, et al.

Enhancing MR image reconstruction using block dictionary learning

[J]. IEEE Access, 2019, 7: 158434-158444.

DOI:10.1109/ACCESS.2019.2949917      [本文引用: 1]

While representing a class of signals in term of sparsifying transform, it is better to use a adapted learned dictionary instead of using a predefined dictionary as proposed in the recent literature. With this improved method, one can represent the sparsest representation for the given set of signals. In order to ease the approximation, atoms of the learned dictionary can further be grouped together to make blocks inside the dictionary that act as a union of small number of subspaces. The block structure of a dictionary can be learned by exploiting the latent structure of the desired signals. Such type of block dictionary leads to block sparse representation of the given signals which can be good for reconstruction of the medical images. In this article, we suggest a framework for MRI reconstruction based upon block sparsifying transform (dictionary). Our technique develops automatic detection of underlying block structure of MR images given maximum block sizes. This is done by iteratively alternating between updating the block structure of the sparsifying transform (dictionary) and block-sparse representation of the MR images. Empirically it is shown that blocksparse representation performs better for recovery of the given MR image with minimum errors.

QU X, CAO X, GUO D, et al.

Combined sparsifying transforms for compressed sensing MRI

[J]. Electron Lett, 2010, 46(2): 121-123.

DOI:10.1049/el.2010.1845      URL     [本文引用: 1]

KNOLL F, BREDIES K, POCK T, et al.

Second order total generalized variation (tgv) for MRI

[J]. Magn Reson Med, 2011, 65(2): 480-491.

DOI:10.1002/mrm.22595      PMID:21264937      [本文引用: 1]

Total variation was recently introduced in many different magnetic resonance imaging applications. The assumption of total variation is that images consist of areas, which are piecewise constant. However, in many practical magnetic resonance imaging situations, this assumption is not valid due to the inhomogeneities of the exciting B1 field and the receive coils. This work introduces the new concept of total generalized variation for magnetic resonance imaging, a new mathematical framework, which is a generalization of the total variation theory and which eliminates these restrictions. Two important applications are considered in this article, image denoising and image reconstruction from undersampled radial data sets with multiple coils. Apart from simulations, experimental results from in vivo measurements are presented where total generalized variation yielded improved image quality over conventional total variation in all cases.Copyright © 2010 Wiley-Liss, Inc.

YANG X M, MEI Y B, HU X Y, et al.

Compressed sensing MRI by integrating deep denoiser and weighted schatten P-norm minimization

[J]. IEEE Signal Proc Lett, 2022, 29: 21-25.

DOI:10.1109/LSP.2021.3122338      URL     [本文引用: 1]

JIANG M F, YUAN Z H, YANG X, et al.

Accelerating CS-MRI reconstruction with fine-tuning wasserstein generative adversarial network

[J]. IEEE Access, 2019, 7: 152347-152357.

DOI:10.1109/Access.6287639      URL     [本文引用: 1]

LI G, LV J, WANG C.

A modified generative adversarial network using spatial and channel-wise attention for CS-MRI reconstruction

[J]. IEEE Access, 2021, 9: 83185-83198.

DOI:10.1109/ACCESS.2021.3086839      URL     [本文引用: 1]

OLAF R, PHILIPP F, THOMAS B.

U-net: convolutional networks for biomedical image segmentation

[C]// Proceedings of the 2015 Medical Imaging Computing and Computer-Assisted Intervention. Munich, Germany: Springer, Cham, 2015: 234-241.

[本文引用: 1]

LIAN Q S, FU L P, CHEN S Z, et al.

A compressed sensing algorithm based on multi-scale residual reconstruction network

[J]. Acta Automatica Sinica, 2019(11): 2082-2091.

[本文引用: 1]

练秋生, 富利鹏, 陈书贞, 等.

基于多尺度残差网络的压缩感知重构算法

[J]. 自动化学报, 2019, 45(11): 2082-2091

[本文引用: 1]

DAI Z X, LI J X, ZHANG X D, et al.

Super-resolution reconstruction of MRI based on DNGAN

[J]. Computer Science, 2022, 49(7): 113-119.

[本文引用: 1]

戴朝霞, 李锦欣, 张向东, 等.

基于DNGAN的磁共振图像超分辨率重建算法

[J]. 计算机科学, 2022, 49(07): 113-119.

[本文引用: 1]

CHAN S H, WANG X, ELGENDY O A.

Plug-and-Play ADMM for image restoration: fixed-point convergence and applications

[J]. IEEE T Compu Imag, 2017, 3(1): 84-98.

[本文引用: 1]

ZHANG J, GHANEM B.

ISTA-Net: Interpretable optimization-inspired deep network for image compressive sensing

[C]// IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, USA: IEEE, 2018: 1828-1837.

[本文引用: 1]

LIU Y, LIU Q, ZHANG M, et al.

IFR-Net: Iterative feature refinement network for compressed sensing MRI

[J]. IEEE T Comput Imag, 6, 434-446.

[本文引用: 1]

SHAH K D, PATEL D K, PATEL H A, et al.

EMED-UNet: An efficient multi-encoder-decoder based UNet for chest X-ray segmentation

[C]// 2022 IEEE Region 10 Symposium (TENSYMP), Mumbai, India, IEEE, 2022: 1-6.

[本文引用: 1]

HONG L T T, THANH N C, LONG T Q,

CRF-EfficientUNet: An improved UNet framework for polyp segmentation in colonoscopy images with combined asymmetric loss function and CRF-RNN layer

[J]. IEEE Access, 2021, 9: 156987-157001.

DOI:10.1109/ACCESS.2021.3129480      URL     [本文引用: 1]

RAMZI Z, CIUCIU P, STARCK J L.

Benchmarking MRI reconstruction neural networks on large public datasets

[J]. Appl Sci, 2020, 10, 1816.

DOI:10.3390/app10051816      URL     [本文引用: 1]

Deep learning is starting to offer promising results for reconstruction in Magnetic Resonance Imaging (MRI). A lot of networks are being developed, but the comparisons remain hard because the frameworks used are not the same among studies, the networks are not properly re-trained, and the datasets used are not the same among comparisons. The recent release of a public dataset, fastMRI, consisting of raw k-space data, encouraged us to write a consistent benchmark of several deep neural networks for MR image reconstruction. This paper shows the results obtained for this benchmark, allowing to compare the networks, and links the open source implementation of all these networks in Keras. The main finding of this benchmark is that it is beneficial to perform more iterations between the image and the measurement spaces compared to having a deeper per-space network.

JETHI A K, MURUGESAN B, RAM K, et al.

Dual-encoder-U-net for fast MRI reconstruction

[C]// 2020 IEEE 17th International Symposium on Biomedical Imaging Workshops (ISBI Workshops), Iowa City, USA: IEEE, 2020: 1-4.

[本文引用: 1]

ZHOU Z, SIDDIQUEE M M R, TAJBAKHSH N, et al.

UNet++: Redesigning skip connections to exploit multiscale features in image segmentation

[J]. IEEE T Med Imaging, 39(6): 1856-1867.

DOI:10.1109/TMI.42      URL     [本文引用: 1]

HE K M, ZHANG X Y, REN S Q, et al.

Deep residual learning for image recognition

[C]// 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, USA: IEEE, 2016: 770-778.

ZBONTAR J, KNOLL F, SRIRAM A, et al.

fastMRI: An open dataset and benchmarks for accelerated MRI

[J]. arXiv preprint arXiv:1811.08839, 2018.

[本文引用: 1]

LI Y Y, LI L, LI X S, et al.

3D Dynamic MRI with Homotopic l0 Minimization Reconstruction

[J]. Chinese J Magn Reson, 2022, 39(01): 20-32.

[本文引用: 1]

李嫣嫣, 李律, 李雪松, 等.

基于同伦l0范数最小化重建的三维动态磁共振成像

[J]. 波谱学杂志, 2022, 39(01): 20-32.

[本文引用: 1]

CHENG J, WANG H, YING L, et al.

Model learning: Primal dual networks for fastMR imaging

[C]// Medical Image Computing and Computer Assisted Intervention - MICCAI 2019, Springer, Cham, 2019: 21-29.

[本文引用: 1]

SCHLEMPER J, CABALLERO J, HAJNAL J V, et al.

A deep cascade of convolutional neural networks for MR image reconstruction

[C]// International conference on information processing in medical imaging, Springer, Cham, 2017: 647-658.

[本文引用: 2]

EO T, JUN Y, KIM T, et al.

KIKI-net: cross-domain convolutional neural networks for reconstructing undersampled magnetic resonance images

[J]. Magn Reson Med, 2018, 80(5): 2188-2201.

DOI:10.1002/mrm.27201      PMID:29624729      [本文引用: 1]

To demonstrate accurate MR image reconstruction from undersampled k-space data using cross-domain convolutional neural networks (CNNs) METHODS: Cross-domain CNNs consist of 3 components: (1) a deep CNN operating on the k-space (KCNN), (2) a deep CNN operating on an image domain (ICNN), and (3) an interleaved data consistency operations. These components are alternately applied, and each CNN is trained to minimize the loss between the reconstructed and corresponding fully sampled k-spaces. The final reconstructed image is obtained by forward-propagating the undersampled k-space data through the entire network.Performances of K-net (KCNN with inverse Fourier transform), I-net (ICNN with interleaved data consistency), and various combinations of the 2 different networks were tested. The test results indicated that K-net and I-net have different advantages/disadvantages in terms of tissue-structure restoration. Consequently, the combination of K-net and I-net is superior to single-domain CNNs. Three MR data sets, the T fluid-attenuated inversion recovery (T FLAIR) set from the Alzheimer's Disease Neuroimaging Initiative and 2 data sets acquired at our local institute (T FLAIR and T weighted), were used to evaluate the performance of 7 conventional reconstruction algorithms and the proposed cross-domain CNNs, which hereafter is referred to as KIKI-net. KIKI-net outperforms conventional algorithms with mean improvements of 2.29 dB in peak SNR and 0.031 in structure similarity.KIKI-net exhibits superior performance over state-of-the-art conventional algorithms in terms of restoring tissue structures and removing aliasing artifacts. The results demonstrate that KIKI-net is applicable up to a reduction factor of 3 to 4 based on variable-density Cartesian undersampling.© 2018 International Society for Magnetic Resonance in Medicine.

RAMANARAYANAN S, MURUGESAN B, RAM K, et al.

DC-WCNN: A deep cascade of wavelet based convolutional neural networks for MR image reconstruction

[C]// 2020 IEEE 17th International Symposium on Biomedical Imaging, Iowa City, USA: IEEE, 2020: 1069-1073.

[本文引用: 1]

/

〈 〉

网站设计版权所有 © 2017 《波谱学杂志》编辑部
地址：湖北省武汉市武昌区小洪山西30号 中科院精密测量科学与技术创新研究院波谱楼 《波谱学杂志》编辑部
邮编：430071　电话/传真：(086)027－87198791   E-mail: magres@wipm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发