Table of Content

25 February 2020, Volume 40 Issue 1 Previous Issue   

For Selected:

View Abstracts

Download Citations EndNote Reference Manager ProCite BibTeX RefWorks

Toggle Thumbnails

Articles

Select

HILBERT PROBLEM 15 AND NONSTANDARD ANALYSIS (I) Banghe LI Acta mathematica scientia,Series B. 2020, 40 (1):  1-15.  DOI: 10.1007/s10473-020-0101-4 Abstract ( 113 )   RICH HTML PDF   Save Hilbert problem 15 required understanding Schubert's book. In this book, reducing to degenerate cases was one of the main methods for enumeration. We found that nonstandard analysis is a suitable tool for making rigorous of Schubert's proofs of some results, which used degeneration method, but are obviously not rigorous. In this paper, we give a rigorous proof for Example 4 in Schubert's book, Chapter 1. §4 according to his idea. This shows that Schubert's intuitive idea is correct, but to make it rigorous a lot of work should be done. References | Related Articles | Metrics

Select

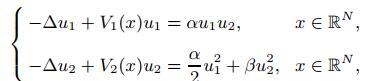
INFINITELY MANY SOLITARY WAVES DUE TO THE SECOND-HARMONIC GENERATION IN QUADRATIC MEDIA Chunhua WANG, Jing ZHOU Acta mathematica scientia,Series B. 2020, 40 (1):  16-34.  DOI: 10.1007/s10473-020-0102-3 Abstract ( 126 )   RICH HTML PDF   Save In this paper, we consider the following coupled Schr?dinger system with χ(2) nonlinearities which arises from second-harmonic generation in quadratic media. Here V1(x) and V2(x) are radially positive functions, 2 ≤ N < 6, α > 0 and α > β. Assume that the potential functions V1(x) and V2(x) satisfy some algebraic decay at infinity. Applying the finite dimensional reduction method, we construct an unbounded sequence of non-radial vector solutions of synchronized type. References | Related Articles | Metrics

Select

COMPLEX SYMMETRIC TOEPLITZ OPERATORS ON THE UNIT POLYDISK AND THE UNIT BALL Cao JIANG, Xingtang DONG, Zehua ZHOU Acta mathematica scientia,Series B. 2020, 40 (1):  35-44.  DOI: 10.1007/s10473-020-103-2 Abstract ( 75 )   RICH HTML PDF   Save In this article, we study complex symmetric Toeplitz operators on the Bergman space and the pluriharmonic Bergman space in several variables. Surprisingly, the necessary and sufficient conditions for Toeplitz operators to be complex symmetric on these two spaces with certain conjugations are just the same. Also, some interesting symmetry properties of complex symmetric Toeplitz operators are obtained. References | Related Articles | Metrics

Select

THE BOUNDEDNESS FOR COMMUTATORS OF ANISOTROPIC CALDERÓN-ZYGMUND OPERATORS Jinxia LI, Baode LI, Jianxun HE Acta mathematica scientia,Series B. 2020, 40 (1):  45-58.  DOI: 10.1007/s10473-020-104-1 Abstract ( 55 )   RICH HTML PDF   Save Let T be an anisotropic Calderón-Zygmund operator and φ : Rn×[0, ∞) → [0, ∞) be an anisotropic Musielak-Orlicz function with φ(x, ·) being an Orlicz function and φ(·, t) being a Muckenhoupt A∞(A) weight. In this paper, our goal is to study two boundedness theorems for commutators of anisotropic Calderón-Zygmund operators. Precisely, when b ∈ BMOw(Rn, A) (a proper subspace of anisotropic bounded mean oscillation space BMO(Rn, A)), the commutator [b, T] is bounded from anisotropic weighted Hardy space Hw1(Rn, A) to weighted Lebesgue space Lw1(Rn) and when b ∈ BMO(Rn) (bounded mean oscillation space), the commutator [b, T] is bounded on Musielak-Orlicz space Lφ(Rn), which are extensions of the isotropic setting. References | Related Articles | Metrics

Select

GROUND STATES FOR FRACTIONAL SCHRÖDINGER EQUATIONS WITH ELECTROMAGNETIC FIELDS AND CRITICAL GROWTH Quanqing LI, Wenbo WANG, Kaimin TENG, Xian WU Acta mathematica scientia,Series B. 2020, 40 (1):  59-74.  DOI: 10.1007/s10473-020-0105-0 Abstract ( 44 )   RICH HTML PDF   Save In this article, we study the following fractional Schrödinger equation with electromagnetic fields and critical growth (-△)Asu + V (x)u = |u|2s*-2u + λf(x,|u|2)u, x ∈ RN, where (-△)As is the fractional magnetic operator with 0 < s < 1, N > 2s, λ > 0, 2s* = 2N/(N-2s), f is a continuous function, V ∈ C(RN, R) and A ∈ C(RN, RN) are the electric and magnetic potentials, respectively. When V and f are asymptotically periodic in x, we prove that the equation has a ground state solution for large λ by Nehari method. References | Related Articles | Metrics

Select

MULTIPLE JEEPS PROBLEM WITH CONTAINER RESTRICTION Xiangying HUA Acta mathematica scientia,Series B. 2020, 40 (1):  75-89.  DOI: 10.1007/s10473-020-0106-z Abstract ( 36 )   RICH HTML PDF   Save Jeep problem is a kind of model of logistics in extreme situation, which has application in exploration and aircraft problems. The optimal distance and driving strategy of multiple jeeps problem are known. We consider multiple jeeps problem with container restriction, which is more complicated in the proof of feasibility and optimality of a driving strategy. We investigate when it can achieve the same optimal distance as without restriction. Based on the non-restricted optimal distance, a new driving strategy is proposed. We provide the necessary and sufficient condition to ensure the feasibility of the strategy, and obtain the maximal feasible distance. References | Related Articles | Metrics

Select

THE EXISTENCE AND LOCAL UNIQUENESS OF MULTI-PEAK POSITIVE SOLUTIONS TO A CLASS OF KIRCHHOFF EQUATION Gongbao LI, Yahui NIU Acta mathematica scientia,Series B. 2020, 40 (1):  90-112.  DOI: 10.1007/s10473-020-0107-y Abstract ( 63 )   RICH HTML PDF   Save In the present paper, we consider the nonlocal Kirchhoff problem - (ε2a + εb∫R3 |▽u|2)△u + u = Q(x)up, u > 0 in R3, where a, b > 0, 1 < p < 5 and ε > 0 is a parameter. Under some assumptions on Q(x), we show the existence and local uniqueness of positive multi-peak solutions by LyapunovSchmidt reduction method and the local Pohozaev identity method, respectly. References | Related Articles | Metrics

Select

N-SOLITON SOLUTION OF THE KUNDU-TYPE EQUATION VIA RIEMANN-HILBERT APPROACH Lili WEN, Ning ZHANG, Engui FAN Acta mathematica scientia,Series B. 2020, 40 (1):  113-126.  DOI: 10.1007/s10473-020-0108-x Abstract ( 38 )   RICH HTML PDF   Save In this article, we focus on investigating the Kundu-type equation with zero boundary condition at infinity. Based on the analytical and symmetric properties of eigenfunctions and spectral matrix of its Lax pair, a Riemann-Hilbert problem for the initial value problem of the Kundu-type equation is constructed. Further through solving the regular and nonregular Riemann-Hilbert problem, a kind of general N-soliton solution of the Kundu-type equation are presented. As special cases of this result, the N-soliton solution of the Kaup-Newell equation, Chen-Lee-Liu equation, and Gerjikov-Ivanov equation can be obtained respectively by choosing different parameters. References | Related Articles | Metrics

Select

HIGHER-ORDER NON-SYMMETRIC DUALITY FOR NONDIFFERENTIABLE MINIMAX FRACTIONAL PROGRAMS WITH SQUARE ROOT TERMS SONALI, Vikas SHARMA, Navdeep KAILEY Acta mathematica scientia,Series B. 2020, 40 (1):  127-140.  DOI: 10.1007/s10473-020-0109-9 Abstract ( 30 )   RICH HTML PDF   Save In this paper, we emphasize on a nondifferentiable minimax fractional programming (NMFP) problem and obtain appropriate duality results for higher-order dual model under higher-order B-(p,r)-invex functions. We provide a nontrivial illustration of a function which belongs to the class of higher-order B-(p,r)-invex but not in the class of second-order B-(p,r)-invex functions already existing in literature. An example of finding a minimax solution of NMFP problem by using higher-order B-(p,r)-invex functions has also been given. Various known results are discussed as particular cases. References | Related Articles | Metrics

Select

EXISTENCE AND STABILITY RESULTS FOR GENERALIZED FRACTIONAL DIFFERENTIAL EQUATIONS A. BEN MAKHLOUF, D. BOUCENNA, M. A. HAMMAMI Acta mathematica scientia,Series B. 2020, 40 (1):  141-154.  DOI: 10.1007/s10473-020-0110-3 Abstract ( 38 )   RICH HTML PDF   Save In this paper, a sufficient conditions to guarantee the existence and stability of solutions for generalized nonlinear fractional differential equations of order α (1 < α < 2) are given. The main results are obtained by using Krasnoselskii's fixed point theorem in a weighted Banach space. Two examples are given to demonstrate the validity of the proposed results. References | Related Articles | Metrics

Select

GLOBAL NONEXISTENCE FOR A VISCOELASTIC WAVE EQUATION WITH ACOUSTIC BOUNDARY CONDITIONS Jiali YU, Yadong SHANG, Huafei DI Acta mathematica scientia,Series B. 2020, 40 (1):  155-169.  DOI: 10.1007/s10473-020-0111-2 Abstract ( 38 )   RICH HTML PDF   Save This paper deals with a class of nonlinear viscoelastic wave equation with damping and source terms utt - △u - △ut - △utt + ∫0tg(t - s)△u(s)ds + ut|ut|m-2=u|u|p-2 with acoustic boundary conditions. Under some appropriate assumption on relaxation function g and the initial data, we prove that the solution blows up in finite time if the positive initial energy satisfies a suitable condition. References | Related Articles | Metrics

Select

OPTIMAL DIVIDEND-PENALTY STRATEGIES FOR INSURANCE RISK MODELS WITH SURPLUS-DEPENDENT PREMIUMS Jingwei LI, Guoxin LIU, Jinyan ZHAO Acta mathematica scientia,Series B. 2020, 40 (1):  170-198.  DOI: 10.1007/s10473-020-0112-1 Abstract ( 45 )   RICH HTML PDF   Save This paper concerns an optimal dividend-penalty problem for the risk models with surplus-dependent premiums. The objective is to maximize the difference of the expected cumulative discounted dividend payments received until the moment of ruin and a discounted penalty payment taken at the moment of ruin. Since the value function may be not smooth enough to be the classical solution of the HJB equation, the viscosity solution is involved. The optimal value function can be characterized as the smallest viscosity supersolution of the HJB equation and the optimal dividend-penalty strategy has a band structure. Finally, some numerical examples with gamma distribution for the claims are analyzed. References | Related Articles | Metrics

Select

LOCAL CONVERGENCE OF INEXACT NEWTON-LIKE METHOD UNDER WEAK LIPSCHITZ CONDITIONS Ioannis K. ARGYROS, Yeol Je CHO, Santhosh GEORGE, Yibin XIAO Acta mathematica scientia,Series B. 2020, 40 (1):  199-210.  DOI: 10.1007/s10473-020-0113-0 Abstract ( 30 )   RICH HTML PDF   Save The paper develops the local convergence of Inexact Newton-Like Method (INLM) for approximating solutions of nonlinear equations in Banach space setting. We employ weak Lipschitz and center-weak Lipschitz conditions to perform the error analysis. The obtained results compare favorably with earlier ones such as [7, 13, 14, 18, 19]. A numerical example is also provided References | Related Articles | Metrics

Select

HERMITIAN-EINSTEIN METRICS FOR HIGGS BUNDLES OVER COMPLETE HERMITIAN MANIFOLDS Debin LIU, Pan ZHANG Acta mathematica scientia,Series B. 2020, 40 (1):  211-225.  DOI: 10.1007/s10473-020-0114-z Abstract ( 32 )   RICH HTML PDF   Save In this paper, we solve the Dirichlet problem for the Hermitian-Einstein equations on Higgs bundles over compact Hermitian manifolds. Then we prove the existence of the Hermitian-Einstein metrics on Higgs bundles over a class of complete Hermitian manifolds. References | Related Articles | Metrics

Select

EXISTENCE OF SOLUTIONS OF nTH-ORDER NONLINEAR DIFFERENCE EQUATIONS WITH GENERAL BOUNDARY CONDITIONS Alberto CABADA, Nikolay DIMITROV Acta mathematica scientia,Series B. 2020, 40 (1):  226-236.  DOI: 10.1007/s10473-020-0115-y Abstract ( 39 )   RICH HTML PDF   Save The aim of this paper is to prove the existence of one or multiple solutions of nonlinear difference equations coupled to a general set of boundary conditions. Before to do this, we construct a discrete operator whose fixed points coincide with the solutions of the problem we are looking for. Moreover, we introduce a strong positiveness condition on the related Green's function that allows us to construct suitable cones where to apply adequate fixed point theorems. Once we have the general existence result, we deduce, as a particular case, the existence of solutions of a second order difference equation with nonlocal perturbed Dirichlet conditions. References | Related Articles | Metrics

Select

THE ENERGY CONSERVATIONS AND LOWER BOUNDS FOR POSSIBLE SINGULAR SOLUTIONS TO THE 3D INCOMPRESSIBLE MHD EQUATIONS Jae-Myoung KIM Acta mathematica scientia,Series B. 2020, 40 (1):  237-244.  DOI: 10.1007/s10473-020-0116-x Abstract ( 54 )   RICH HTML PDF   Save In this note, we give a new proof to the energy conservation for the weak solutions of the incompressible 3D MHD equations. Moreover, we give the lower bounds for possible singular solutions to the incompressible 3D MHD equations. References | Related Articles | Metrics

Select

COMPLEX INTERPOLATION OF NONCOMMUTATIVE HARDY SPACES ASSOCIATED WITH SEMIFINITE VON NEUMANN ALGEBRAS Turdebek N. BEKJAN, Kordan N. OSPANOV Acta mathematica scientia,Series B. 2020, 40 (1):  245-260.  DOI: 10.1007/s10473-020-0117-9 Abstract ( 33 )   RICH HTML PDF   Save We proved a complex interpolation theorem of noncommutative Hardy spaces associated with semi-finite von Neumann algebras and extend the Riesz type factorization to the semi-finite case. References | Related Articles | Metrics

Select

GLOBAL SIMPLE WAVE SOLUTIONS TO A KIND OF TWO DIMENSIONAL HYPERBOLIC SYSTEM OF CONSERVATION LAWS Jianli LIU, Jie XUE Acta mathematica scientia,Series B. 2020, 40 (1):  261-271.  DOI: 10.1007/s10473-020-0118-8 Abstract ( 37 )   RICH HTML PDF   Save This paper is concerned with the simple waves of a kind of two dimensional hyperbolic system of conservation laws, which can be obtained from the two dimensional relativistic membrane equation in Minkowski space. Using wave decomposition method, we get that a flow adjacent to a nonconstant state can be a global simple wave. Furthermore, the flow is covered by three families of characteristics, in which the first family of characteristics is straight and the others are curved, which is different to the almost related results. References | Related Articles | Metrics

Select

BOUNDEDNESS OF MULTILINEAR LITTLEWOOD-PALEY OPERATORS ON AMALGAM-CAMPANATO SPACES Xiang LI, Qianjun HE, Dunyan YAN Acta mathematica scientia,Series B. 2020, 40 (1):  272-292.  DOI: 10.1007/s10473-020-0119-7 Abstract ( 48 )   RICH HTML PDF   Save In this paper, we consider the boundedness of multilinear Littlewood-Paley operators which include multilinear g-function, multilinear Lusin’s area integral and multilinear Littlewood-Paley gλ*-function. Furthermore, norm inequalities of the above operators hold on the corresponding Amalgam-Campanato spaces. References | Related Articles | Metrics