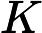数学物理学报(英文版) ›› 2021, Vol. 41 ›› Issue (6): 2123-2135.doi: 10.1007/s10473-021-0619-x
ANALYTIC PHASE RETRIEVAL BASED ON INTENSITY MEASUREMENTS
曲伟1, 钱涛2, 邓冠铁3, 李尤发4, 周春旭4
- 1. Department of Applied Mathematics, School of Mathematics and Physics, University of Science and Technology Beijing, Beijing 100083, China;
2. Macau Center for Mathematical Sciences, Macau University of Science and Technolofy, China;
3. School of Mathematical Sciences, Beijing Normal University, Beijing 100875, China;
4. College of Mathematics and Information Science, Guangxi University, Nanning 530004, China
ANALYTIC PHASE RETRIEVAL BASED ON INTENSITY MEASUREMENTS
Wei QU1, Tao QIAN2, Guantie DENG3, Youfa LI4, Chunxu ZHOU4
- 1. Department of Applied Mathematics, School of Mathematics and Physics, University of Science and Technology Beijing, Beijing 100083, China;
2. Macau Center for Mathematical Sciences, Macau University of Science and Technolofy, China;
3. School of Mathematical Sciences, Beijing Normal University, Beijing 100875, China;
4. College of Mathematics and Information Science, Guangxi University, Nanning 530004, China
摘要: This paper concerns the reconstruction of a function in the Hardy space of the unit disc by using a sample value and certain -intensity measurements where and is the -th term of the Gram-Schmidt orthogonalization of the Szegökernels or their multiple forms. Three schemes are presented. The first two schemes each directly obtain all the function values In the first one we use Nevanlinna's inner and outer function factorization which merely requires the -intensity measurements equivalent to know the modulus In the second scheme we do not use deep complex analysis, but require some - and -intensity measurements. The third scheme, as an application of AFD, gives sparse representation of converging quickly in the energy sense, depending on consecutively selected maximal -intensity measurements
中图分类号:
- 30H10