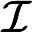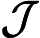数学物理学报(英文版) ›› 2025, Vol. 45 ›› Issue (2): 473-492.doi: 10.1007/s10473-025-0211-x
ON THE MEASURE CONCENTRATION OF INFINITELY DIVISIBLE DISTRIBUTIONS
Jing Zhang1, Zechun Hu2, Wei Sun3,*
- 1. School of Mathematics and Statistics, Hainan Normal University, Haikou 571158, China;
2. College of Mathematics, Sichuan University, Chengdu 610065, China;
3. Department of Mathematics and Statistics, Concordia University, Montreal H3G 1M8, Canada
ON THE MEASURE CONCENTRATION OF INFINITELY DIVISIBLE DISTRIBUTIONS
Jing Zhang1, Zechun Hu2, Wei Sun3,*
- 1. School of Mathematics and Statistics, Hainan Normal University, Haikou 571158, China;
2. College of Mathematics, Sichuan University, Chengdu 610065, China;
3. Department of Mathematics and Statistics, Concordia University, Montreal H3G 1M8, Canada
摘要: Let be the set of all infinitely divisible random variables with finite second moments, , and . Firstly, we prove that . Secondly, we find the exact values of and for the cases that is the set of all geometric random variables, symmetric geometric random variables, Poisson random variables and symmetric Poisson random variables, respectively. As a consequence, we obtain that and .
中图分类号:
- 60E07