[1] d'Humieres D, Lallemand P, Frisch U. Lattice gas models for 3D hydrodynamics. Europhysics Letters, 1986, 2(4):291
[2] Leray J. Sur le mouvement d'un liquide visqueux emplissant l'espace. Acta Mathematica, 1934, 63:193-248
[3] Fujita H, Kato T. On the Navier-Stokes initial value problem. I. Archive for Rational Mechanics and Analysis, 1964, 16(4):269-315
[4] Kato T, Fujita H. On the nonstationary Navier-Stokes system. Rendiconti del Seminario Matematico della Universit di Padova, 1962, 32:243-260
[5] Kato T. StrongL p-solutions of the Navier-Stokes equation in Rm, with applications to weak solutions. Mathematische Zeitschrift, 1984, 187(4):471-480
[6] Cannone M. Paraproduits et Navier-Stokes Diderot Editeur. Arts et Sciences, 1995
[7] Wan R, Jia H. Global well-posedness for the 3D Navier-Sokes equations with a large component of vorticity. Journal of Mathematical Analysis and Applications, 2019, 469(2):504-524
[8] Giga Y, Miyakawa T. Navier-Stokes flow in R3 with measures as initial vorticity and Morrey spaces. Communications in Partial Differential Equations, 1989, 14(5):577-618
[9] Kato T. Strong solutions of the Navier-Stokes equation in Morrey spaces. Boletim da Sociedade Brasileira de Matemtica-Bulletin/Brazilian Mathematical Society, 1992, 22(2):127-155
[10] Taylor M E. Analysis on Morrey spaces and applications to Navier-Stokes and other evolution equations. Communications in Partial Differential Equations, 1992, 17(9/10):1407-1456
[11] Koch H, Tataru D. Well-posedness for the Navier-Stokes equations. Advances in Mathematics, 2001, 157(1):22-35
[12] Bourgain J, Pavlovic N. Ill-posedness of the Navier-Stokes equations in a critical space in 3D. Journal of Functional Analysis, 2008, 255(9):2233-2247
[13] Biswas A, Swanson D. Gevrey regularity of solutions to the 3-D Navier-Stokes equations with weighted p initial data. Indiana University Mathematics Journal, 2007, 56(3):1157-1188
[14] Konieczny P, Yoneda T. On dispersive effect of the Coriolis force for the stationary Navier-Stokes equations. Journal of Differential Equations, 2011, 250(10):3859-3873
[15] Lei Z, Lin F. Global mild solutions of Navier-Stokes equations. Communications on Pure and Applied Mathematics, 2011, 64(9):1297-1304
[16] Lions J L. Quelques mthodes de rsolution des problemes aux limites non linaires. 1969
[17] Wu J. Generalized MHD equations. Journal of Differential Equations, 2003, 195(2):284-312
[18] Wu J. Lower bounds for an integral involving fractional Laplacians and the generalized Navier-Stokes equations in Besov spaces. Communications in Mathematical Physics, 2006, 263(3):803-831
[19] Wang Y, Xiao J. Well/ill-posedness for the dissipative Navier-Stokes system in generalized Carleson measure spaces. Advances in Nonlinear Analysis, 2017, 8(1):203-224
[20] Li P, Xiao J, Yang Q. Global mild solutions to modified Navier-Stokes equations with small initial data in critical Besov-Q spaces. Electronic Journal of Differential Equations, 2014, 2014(185):1-37
[21] Dong H, Li D. Optimal local smoothing and analyticity rate estimates for the generalized Navier-Stokes equations. Communications in Mathematical Sciences, 2009, 7(1):67-80
[22] Xiao J. Homothetic variant of fractional Sobolev space with application to Navier-Stokes system revisited. Dyn Partial Differ Equ, 2014, 11(2):167-181
[23] Li P, Zhai Z. Well-posedness and regularity of generalized Navier-Stokes equations in some critical Q-spaces. Journal of Functional Analysis, 2010, 259(10):2457-2519
[24] Yu X, Zhai Z. Well-posedness for fractional Navier-Stokes equations in critical spaces close to                 . Math Method Appl Sci, 2012, 35(6):676-683 . Math Method Appl Sci, 2012, 35(6):676-683
[25] Deng C, Yao X. Well-posedness and ill-posedness for the 3D generalized Navier-Stokes equations in           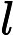 . Dynamical Systems, 2014, 34(2):437-459 . Dynamical Systems, 2014, 34(2):437-459
[26] Yu X, Zhai Z. Well-posedness for fractional Navier-Stokes equations in the largest critical spaces. Comm Pure Appl Anal, 2012, 11(5):1809-1823
[27] El Baraka A, Toumlilin M. Global well-posedness for fractional Navier-Stokes equations in critical FourierBesov-Morrey spaces. Moroccan Journal of Pure and Applied Analysis, 2017, 3(1):1-13
[28] Orlicz W. ber konjugierte exponentenfolgen. Studia Mathematica, 1931, 3(1):200-211
[29] Orlicz W. ber eine gewisse Klasse von Rumen vom Typus B. Bull Int Acad Pol Ser A, 1932, 8(9):207-220
[30] Musielak J. Modular spaces//Orlicz Spaces and Modular Spaces. Berlin, Heidelberg:Springer, 1983:1-32
[31] Nakano H. Topology and Linear Topological Spaces Ⅲ. Maruzen Company, 1951
[32] Kovik O, Rkosnk J. On spaces Lp(x) and Wk,p(x). Czechoslovak Mathematical Journal, 1991, 41(4):592-618
[33] Cruz-Unbe D. The Hardy-Littlewood maximal operator on variable-Lp spaces//Seminar of Mathematical Analysis:Proceedings, Universities of Malaga and Seville (Spain), September 2002-February 2003. 2003, 64(147). Universidad de Sevilla
[34] Diening L. Maximal function on generalized Lebesgue spaces Lp(x). Univ Math Fak, 2002
[35] Cruz-Uribe D, Diening L, Hst P. The maximal operator on weighted variable Lebesgue spaces. Fractional Calculus and Applied Analysis, 2011, 14(3):361-374
[36] Cruz-Uribe D V, Fiorenza A. Variable Lebesgue Spaces:Foundations and Harmonic Analysis. Springer Science Business Media, 2013
[37] Acerbi E, Mingione G. Regularity results for stationary electro-rheological fluids. Archive for Rational Mechanics and Analysis, 2002, 164(3):213-259
[38] Ruzicka M. Electrorheological Fluids:Modeling and Mathematical Theory. Springer Science and Business Media, 2000
[39] Chen Y, Levine S, Rao M. Variable exponent, linear growth functionals in image restoration. SIAM Journal on Applied Mathematics, 200666(4):1383-1406
[40] Fan X. Global C1, Cα regularity for variable exponent elliptic equations in divergence form. Journal of Differential Equations, 2007, 235(2):397-417
[41] Luxenberg W. Banach Function Spaces. Assen, 1955
[42] Almeida A, Caetano A. Variable exponent Besov-Morrey spaces. J Fourier Anal Appl, 2020, 26(1):Art 5
[43] Ru S, Abidin M Z. Global well-posedness of the incompressible fractional Navier-Stokes equations in FourierBesov spaces with variable exponents. Computers & Mathematics with Applications, 2019, 77(4):1082-1090
[44] El Baraka A, Toumlilin M. Global well-posedness and decay results for 3D generalized magnetohydrodynamic equations in critical Fourier-Besov-Morrey spaces. Electronic Journal of Differential Equations, 2017, 65:1-20
[45] Almeida A, Hst P. Besov spaces with variable smoothness and integrability. Journal of Functional Analysis, 2010, 258(5):1628-1655 |