Queueing system with a removable service station
1
1963
... 随着学者们对排队系统研究的深入和实际应用的需要,近几十年来在对有休假机制和控制策略的排队系统研究方面取得了较大的进展.早期的经典工作有Yadin和Naor的N -策略[1], Balachandran的D -策略[2], Yechiali和Heyman的T -策略[3], Doshi的休假排队系统[4]等.从已有的研究情况看,各个经典控制策略和休假机制都是从不同的角度提出的,其目的就是在平衡顾客等待时间的同时降低系统的成本,增加系统的收入.在一些经典工作之后,一些推广研究文献陆续出现[5-15].考虑到单一策略有各自的优缺点,例如,当生产制造环境发生改变并且系统拥有者想转换成另一种控制策略时,在这种情况下抛弃现有的硬件系统是不现实的,从而联合控制策略就是一种可供选择的好方案,能更好地解决这一实际问题.因此,结合实际背景,一些作者提出了一些具有联合控制策略的排队系统模型[16-28].文献[24]建立了有{\rm Min}(N, D) -策略控制的M/G/1排队模型,文献[25]在文献[24]的基础上,把到达过程推广到马尔科夫过程,分析了有{\rm Min}(N, D) -策略控制的MAP/G/1排队系统,文献[26]进一步讨论了有{\rm Min}(N, D) -策略的M/G/1排队系统,文献[27]在文献[26]的基础上,把二维控制策略(N, D)与服务员的休假机制结合起来,构造了一个联合的{\rm Min}(N, D, V) -控制策略,使用全概率分解技术和利用拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布和稳态队长分布,同时,给出了稳态队长的随机分解结果和附加队长分布的显示表达式.最后在建立费用模型的基础上讨论了二维最优控制策略,并与单一的控制策略进行了比较分析.文献[28]讨论了基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统. ...
Control policies for a single server system
1
1973
... 随着学者们对排队系统研究的深入和实际应用的需要,近几十年来在对有休假机制和控制策略的排队系统研究方面取得了较大的进展.早期的经典工作有Yadin和Naor的N -策略[1], Balachandran的D -策略[2], Yechiali和Heyman的T -策略[3], Doshi的休假排队系统[4]等.从已有的研究情况看,各个经典控制策略和休假机制都是从不同的角度提出的,其目的就是在平衡顾客等待时间的同时降低系统的成本,增加系统的收入.在一些经典工作之后,一些推广研究文献陆续出现[5-15].考虑到单一策略有各自的优缺点,例如,当生产制造环境发生改变并且系统拥有者想转换成另一种控制策略时,在这种情况下抛弃现有的硬件系统是不现实的,从而联合控制策略就是一种可供选择的好方案,能更好地解决这一实际问题.因此,结合实际背景,一些作者提出了一些具有联合控制策略的排队系统模型[16-28].文献[24]建立了有{\rm Min}(N, D) -策略控制的M/G/1排队模型,文献[25]在文献[24]的基础上,把到达过程推广到马尔科夫过程,分析了有{\rm Min}(N, D) -策略控制的MAP/G/1排队系统,文献[26]进一步讨论了有{\rm Min}(N, D) -策略的M/G/1排队系统,文献[27]在文献[26]的基础上,把二维控制策略(N, D)与服务员的休假机制结合起来,构造了一个联合的{\rm Min}(N, D, V) -控制策略,使用全概率分解技术和利用拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布和稳态队长分布,同时,给出了稳态队长的随机分解结果和附加队长分布的显示表达式.最后在建立费用模型的基础上讨论了二维最优控制策略,并与单一的控制策略进行了比较分析.文献[28]讨论了基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统. ...
T-policy for the M/G/1 queue
1
1977
... 随着学者们对排队系统研究的深入和实际应用的需要,近几十年来在对有休假机制和控制策略的排队系统研究方面取得了较大的进展.早期的经典工作有Yadin和Naor的N -策略[1], Balachandran的D -策略[2], Yechiali和Heyman的T -策略[3], Doshi的休假排队系统[4]等.从已有的研究情况看,各个经典控制策略和休假机制都是从不同的角度提出的,其目的就是在平衡顾客等待时间的同时降低系统的成本,增加系统的收入.在一些经典工作之后,一些推广研究文献陆续出现[5-15].考虑到单一策略有各自的优缺点,例如,当生产制造环境发生改变并且系统拥有者想转换成另一种控制策略时,在这种情况下抛弃现有的硬件系统是不现实的,从而联合控制策略就是一种可供选择的好方案,能更好地解决这一实际问题.因此,结合实际背景,一些作者提出了一些具有联合控制策略的排队系统模型[16-28].文献[24]建立了有{\rm Min}(N, D) -策略控制的M/G/1排队模型,文献[25]在文献[24]的基础上,把到达过程推广到马尔科夫过程,分析了有{\rm Min}(N, D) -策略控制的MAP/G/1排队系统,文献[26]进一步讨论了有{\rm Min}(N, D) -策略的M/G/1排队系统,文献[27]在文献[26]的基础上,把二维控制策略(N, D)与服务员的休假机制结合起来,构造了一个联合的{\rm Min}(N, D, V) -控制策略,使用全概率分解技术和利用拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布和稳态队长分布,同时,给出了稳态队长的随机分解结果和附加队长分布的显示表达式.最后在建立费用模型的基础上讨论了二维最优控制策略,并与单一的控制策略进行了比较分析.文献[28]讨论了基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统. ...
Queueing systems with vacations-A survey
1
1986
... 随着学者们对排队系统研究的深入和实际应用的需要,近几十年来在对有休假机制和控制策略的排队系统研究方面取得了较大的进展.早期的经典工作有Yadin和Naor的N -策略[1], Balachandran的D -策略[2], Yechiali和Heyman的T -策略[3], Doshi的休假排队系统[4]等.从已有的研究情况看,各个经典控制策略和休假机制都是从不同的角度提出的,其目的就是在平衡顾客等待时间的同时降低系统的成本,增加系统的收入.在一些经典工作之后,一些推广研究文献陆续出现[5-15].考虑到单一策略有各自的优缺点,例如,当生产制造环境发生改变并且系统拥有者想转换成另一种控制策略时,在这种情况下抛弃现有的硬件系统是不现实的,从而联合控制策略就是一种可供选择的好方案,能更好地解决这一实际问题.因此,结合实际背景,一些作者提出了一些具有联合控制策略的排队系统模型[16-28].文献[24]建立了有{\rm Min}(N, D) -策略控制的M/G/1排队模型,文献[25]在文献[24]的基础上,把到达过程推广到马尔科夫过程,分析了有{\rm Min}(N, D) -策略控制的MAP/G/1排队系统,文献[26]进一步讨论了有{\rm Min}(N, D) -策略的M/G/1排队系统,文献[27]在文献[26]的基础上,把二维控制策略(N, D)与服务员的休假机制结合起来,构造了一个联合的{\rm Min}(N, D, V) -控制策略,使用全概率分解技术和利用拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布和稳态队长分布,同时,给出了稳态队长的随机分解结果和附加队长分布的显示表达式.最后在建立费用模型的基础上讨论了二维最优控制策略,并与单一的控制策略进行了比较分析.文献[28]讨论了基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统. ...
Modified T vacation policy for an M/G/1 queueing system with an unreliable server and startup
1
2005
... 随着学者们对排队系统研究的深入和实际应用的需要,近几十年来在对有休假机制和控制策略的排队系统研究方面取得了较大的进展.早期的经典工作有Yadin和Naor的N -策略[1], Balachandran的D -策略[2], Yechiali和Heyman的T -策略[3], Doshi的休假排队系统[4]等.从已有的研究情况看,各个经典控制策略和休假机制都是从不同的角度提出的,其目的就是在平衡顾客等待时间的同时降低系统的成本,增加系统的收入.在一些经典工作之后,一些推广研究文献陆续出现[5-15].考虑到单一策略有各自的优缺点,例如,当生产制造环境发生改变并且系统拥有者想转换成另一种控制策略时,在这种情况下抛弃现有的硬件系统是不现实的,从而联合控制策略就是一种可供选择的好方案,能更好地解决这一实际问题.因此,结合实际背景,一些作者提出了一些具有联合控制策略的排队系统模型[16-28].文献[24]建立了有{\rm Min}(N, D) -策略控制的M/G/1排队模型,文献[25]在文献[24]的基础上,把到达过程推广到马尔科夫过程,分析了有{\rm Min}(N, D) -策略控制的MAP/G/1排队系统,文献[26]进一步讨论了有{\rm Min}(N, D) -策略的M/G/1排队系统,文献[27]在文献[26]的基础上,把二维控制策略(N, D)与服务员的休假机制结合起来,构造了一个联合的{\rm Min}(N, D, V) -控制策略,使用全概率分解技术和利用拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布和稳态队长分布,同时,给出了稳态队长的随机分解结果和附加队长分布的显示表达式.最后在建立费用模型的基础上讨论了二维最优控制策略,并与单一的控制策略进行了比较分析.文献[28]讨论了基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统. ...
Analysis of the M^X/G/1 queue under D-policy
0
2005
Optical control of the D-policy M/G/1 queueing system with server breakdowns
0
2008
Analysis of D-policy discrete-time Geo/G/1 queue with second J-optional service and unreliable server
0
2017
The queue-length distribution for M^X/G/1 queue with single server vacation
0
2000
多级适应性休假M^X/G/1排队系统的队长分布
0
2007
多级适应性休假M^X/G/1排队系统的队长分布
0
2007
The departure process of the M/G/1 queueing model with server vacation and exhaustive service discipline
0
1994
Discrete-time queue with unreliable server and multiple adaptive delayed vacation
0
2008
GI/Geom/1/MWV queue with changeover time and searching for the optimum service rate in working vacation period
0
2011
The recursive solution for Geom/G/1(E, SV) queue with feedback and single server vacation
0
2011
Performance analysis of a discrete-time Geo/G/1 queue with randomized vacations and at most J vacations
1
2013
... 随着学者们对排队系统研究的深入和实际应用的需要,近几十年来在对有休假机制和控制策略的排队系统研究方面取得了较大的进展.早期的经典工作有Yadin和Naor的N -策略[1], Balachandran的D -策略[2], Yechiali和Heyman的T -策略[3], Doshi的休假排队系统[4]等.从已有的研究情况看,各个经典控制策略和休假机制都是从不同的角度提出的,其目的就是在平衡顾客等待时间的同时降低系统的成本,增加系统的收入.在一些经典工作之后,一些推广研究文献陆续出现[5-15].考虑到单一策略有各自的优缺点,例如,当生产制造环境发生改变并且系统拥有者想转换成另一种控制策略时,在这种情况下抛弃现有的硬件系统是不现实的,从而联合控制策略就是一种可供选择的好方案,能更好地解决这一实际问题.因此,结合实际背景,一些作者提出了一些具有联合控制策略的排队系统模型[16-28].文献[24]建立了有{\rm Min}(N, D) -策略控制的M/G/1排队模型,文献[25]在文献[24]的基础上,把到达过程推广到马尔科夫过程,分析了有{\rm Min}(N, D) -策略控制的MAP/G/1排队系统,文献[26]进一步讨论了有{\rm Min}(N, D) -策略的M/G/1排队系统,文献[27]在文献[26]的基础上,把二维控制策略(N, D)与服务员的休假机制结合起来,构造了一个联合的{\rm Min}(N, D, V) -控制策略,使用全概率分解技术和利用拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布和稳态队长分布,同时,给出了稳态队长的随机分解结果和附加队长分布的显示表达式.最后在建立费用模型的基础上讨论了二维最优控制策略,并与单一的控制策略进行了比较分析.文献[28]讨论了基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统. ...
System capacity optimization design and optimal threshold N^* for a Geo/G/1 discrete-time queue with single server vacation and under the control of {\rm Min}(N, V)-policy
1
2016
... 随着学者们对排队系统研究的深入和实际应用的需要,近几十年来在对有休假机制和控制策略的排队系统研究方面取得了较大的进展.早期的经典工作有Yadin和Naor的N -策略[1], Balachandran的D -策略[2], Yechiali和Heyman的T -策略[3], Doshi的休假排队系统[4]等.从已有的研究情况看,各个经典控制策略和休假机制都是从不同的角度提出的,其目的就是在平衡顾客等待时间的同时降低系统的成本,增加系统的收入.在一些经典工作之后,一些推广研究文献陆续出现[5-15].考虑到单一策略有各自的优缺点,例如,当生产制造环境发生改变并且系统拥有者想转换成另一种控制策略时,在这种情况下抛弃现有的硬件系统是不现实的,从而联合控制策略就是一种可供选择的好方案,能更好地解决这一实际问题.因此,结合实际背景,一些作者提出了一些具有联合控制策略的排队系统模型[16-28].文献[24]建立了有{\rm Min}(N, D) -策略控制的M/G/1排队模型,文献[25]在文献[24]的基础上,把到达过程推广到马尔科夫过程,分析了有{\rm Min}(N, D) -策略控制的MAP/G/1排队系统,文献[26]进一步讨论了有{\rm Min}(N, D) -策略的M/G/1排队系统,文献[27]在文献[26]的基础上,把二维控制策略(N, D)与服务员的休假机制结合起来,构造了一个联合的{\rm Min}(N, D, V) -控制策略,使用全概率分解技术和利用拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布和稳态队长分布,同时,给出了稳态队长的随机分解结果和附加队长分布的显示表达式.最后在建立费用模型的基础上讨论了二维最优控制策略,并与单一的控制策略进行了比较分析.文献[28]讨论了基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统. ...
Queue size distribution of Geo/G/1 queue under the {\rm Min}(N, D)-policy
0
2016
{\rm Min}(N, V) -策略休假的M/G/1排队系统分析
0
2006
{\rm Min}(N, V) -策略休假的M/G/1排队系统分析
0
2006
基于多重休假的{\rm Min}(N, V) -策略M/G/1排队系统的队长分布
0
2014
基于多重休假的{\rm Min}(N, V) -策略M/G/1排队系统的队长分布
0
2014
基于单重休假的{\rm Min}(N, V) -策略M/G/1排队系统分析
0
2014
基于单重休假的{\rm Min}(N, V) -策略M/G/1排队系统分析
0
2014
具有多级适应性休假和{\rm Min}(N, V) -策略控制的M/G/1排队系统
0
2017
具有多级适应性休假和{\rm Min}(N, V) -策略控制的M/G/1排队系统
0
2017
具有{\rm Min}(N, D) -策略控制的M/G/1可修排队系统及最优控制策略
0
2017
具有{\rm Min}(N, D) -策略控制的M/G/1可修排队系统及最优控制策略
0
2017
具有温储备失效特征和单重休假{\rm Min}(N, V) -控制策略的M/G/1可修排队系统
0
2017
具有温储备失效特征和单重休假{\rm Min}(N, V) -控制策略的M/G/1可修排队系统
0
2017
The performance of the M/G/1 queue under the dyadic {\rm Min}(N, D)-policy and its cost optimization
2
2008
... 随着学者们对排队系统研究的深入和实际应用的需要,近几十年来在对有休假机制和控制策略的排队系统研究方面取得了较大的进展.早期的经典工作有Yadin和Naor的N -策略[1], Balachandran的D -策略[2], Yechiali和Heyman的T -策略[3], Doshi的休假排队系统[4]等.从已有的研究情况看,各个经典控制策略和休假机制都是从不同的角度提出的,其目的就是在平衡顾客等待时间的同时降低系统的成本,增加系统的收入.在一些经典工作之后,一些推广研究文献陆续出现[5-15].考虑到单一策略有各自的优缺点,例如,当生产制造环境发生改变并且系统拥有者想转换成另一种控制策略时,在这种情况下抛弃现有的硬件系统是不现实的,从而联合控制策略就是一种可供选择的好方案,能更好地解决这一实际问题.因此,结合实际背景,一些作者提出了一些具有联合控制策略的排队系统模型[16-28].文献[24]建立了有{\rm Min}(N, D) -策略控制的M/G/1排队模型,文献[25]在文献[24]的基础上,把到达过程推广到马尔科夫过程,分析了有{\rm Min}(N, D) -策略控制的MAP/G/1排队系统,文献[26]进一步讨论了有{\rm Min}(N, D) -策略的M/G/1排队系统,文献[27]在文献[26]的基础上,把二维控制策略(N, D)与服务员的休假机制结合起来,构造了一个联合的{\rm Min}(N, D, V) -控制策略,使用全概率分解技术和利用拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布和稳态队长分布,同时,给出了稳态队长的随机分解结果和附加队长分布的显示表达式.最后在建立费用模型的基础上讨论了二维最优控制策略,并与单一的控制策略进行了比较分析.文献[28]讨论了基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统. ...
... ]在文献[24]的基础上,把到达过程推广到马尔科夫过程,分析了有{\rm Min}(N, D) -策略控制的MAP/G/1排队系统,文献[26]进一步讨论了有{\rm Min}(N, D) -策略的M/G/1排队系统,文献[27]在文献[26]的基础上,把二维控制策略(N, D)与服务员的休假机制结合起来,构造了一个联合的{\rm Min}(N, D, V) -控制策略,使用全概率分解技术和利用拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布和稳态队长分布,同时,给出了稳态队长的随机分解结果和附加队长分布的显示表达式.最后在建立费用模型的基础上讨论了二维最优控制策略,并与单一的控制策略进行了比较分析.文献[28]讨论了基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统. ...
Analysis of the MAP/G/1 queue under the {\rm Min}(N, D)-policy
1
2010
... 随着学者们对排队系统研究的深入和实际应用的需要,近几十年来在对有休假机制和控制策略的排队系统研究方面取得了较大的进展.早期的经典工作有Yadin和Naor的N -策略[1], Balachandran的D -策略[2], Yechiali和Heyman的T -策略[3], Doshi的休假排队系统[4]等.从已有的研究情况看,各个经典控制策略和休假机制都是从不同的角度提出的,其目的就是在平衡顾客等待时间的同时降低系统的成本,增加系统的收入.在一些经典工作之后,一些推广研究文献陆续出现[5-15].考虑到单一策略有各自的优缺点,例如,当生产制造环境发生改变并且系统拥有者想转换成另一种控制策略时,在这种情况下抛弃现有的硬件系统是不现实的,从而联合控制策略就是一种可供选择的好方案,能更好地解决这一实际问题.因此,结合实际背景,一些作者提出了一些具有联合控制策略的排队系统模型[16-28].文献[24]建立了有{\rm Min}(N, D) -策略控制的M/G/1排队模型,文献[25]在文献[24]的基础上,把到达过程推广到马尔科夫过程,分析了有{\rm Min}(N, D) -策略控制的MAP/G/1排队系统,文献[26]进一步讨论了有{\rm Min}(N, D) -策略的M/G/1排队系统,文献[27]在文献[26]的基础上,把二维控制策略(N, D)与服务员的休假机制结合起来,构造了一个联合的{\rm Min}(N, D, V) -控制策略,使用全概率分解技术和利用拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布和稳态队长分布,同时,给出了稳态队长的随机分解结果和附加队长分布的显示表达式.最后在建立费用模型的基础上讨论了二维最优控制策略,并与单一的控制策略进行了比较分析.文献[28]讨论了基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统. ...
基于{\rm Min}(N, D) -策略的M/G/1排队系统的队长分布及最优策略
2
2015
... 随着学者们对排队系统研究的深入和实际应用的需要,近几十年来在对有休假机制和控制策略的排队系统研究方面取得了较大的进展.早期的经典工作有Yadin和Naor的N -策略[1], Balachandran的D -策略[2], Yechiali和Heyman的T -策略[3], Doshi的休假排队系统[4]等.从已有的研究情况看,各个经典控制策略和休假机制都是从不同的角度提出的,其目的就是在平衡顾客等待时间的同时降低系统的成本,增加系统的收入.在一些经典工作之后,一些推广研究文献陆续出现[5-15].考虑到单一策略有各自的优缺点,例如,当生产制造环境发生改变并且系统拥有者想转换成另一种控制策略时,在这种情况下抛弃现有的硬件系统是不现实的,从而联合控制策略就是一种可供选择的好方案,能更好地解决这一实际问题.因此,结合实际背景,一些作者提出了一些具有联合控制策略的排队系统模型[16-28].文献[24]建立了有{\rm Min}(N, D) -策略控制的M/G/1排队模型,文献[25]在文献[24]的基础上,把到达过程推广到马尔科夫过程,分析了有{\rm Min}(N, D) -策略控制的MAP/G/1排队系统,文献[26]进一步讨论了有{\rm Min}(N, D) -策略的M/G/1排队系统,文献[27]在文献[26]的基础上,把二维控制策略(N, D)与服务员的休假机制结合起来,构造了一个联合的{\rm Min}(N, D, V) -控制策略,使用全概率分解技术和利用拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布和稳态队长分布,同时,给出了稳态队长的随机分解结果和附加队长分布的显示表达式.最后在建立费用模型的基础上讨论了二维最优控制策略,并与单一的控制策略进行了比较分析.文献[28]讨论了基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统. ...
... ]在文献[26]的基础上,把二维控制策略(N, D)与服务员的休假机制结合起来,构造了一个联合的{\rm Min}(N, D, V) -控制策略,使用全概率分解技术和利用拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布和稳态队长分布,同时,给出了稳态队长的随机分解结果和附加队长分布的显示表达式.最后在建立费用模型的基础上讨论了二维最优控制策略,并与单一的控制策略进行了比较分析.文献[28]讨论了基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统. ...
基于{\rm Min}(N, D) -策略的M/G/1排队系统的队长分布及最优策略
2
2015
... 随着学者们对排队系统研究的深入和实际应用的需要,近几十年来在对有休假机制和控制策略的排队系统研究方面取得了较大的进展.早期的经典工作有Yadin和Naor的N -策略[1], Balachandran的D -策略[2], Yechiali和Heyman的T -策略[3], Doshi的休假排队系统[4]等.从已有的研究情况看,各个经典控制策略和休假机制都是从不同的角度提出的,其目的就是在平衡顾客等待时间的同时降低系统的成本,增加系统的收入.在一些经典工作之后,一些推广研究文献陆续出现[5-15].考虑到单一策略有各自的优缺点,例如,当生产制造环境发生改变并且系统拥有者想转换成另一种控制策略时,在这种情况下抛弃现有的硬件系统是不现实的,从而联合控制策略就是一种可供选择的好方案,能更好地解决这一实际问题.因此,结合实际背景,一些作者提出了一些具有联合控制策略的排队系统模型[16-28].文献[24]建立了有{\rm Min}(N, D) -策略控制的M/G/1排队模型,文献[25]在文献[24]的基础上,把到达过程推广到马尔科夫过程,分析了有{\rm Min}(N, D) -策略控制的MAP/G/1排队系统,文献[26]进一步讨论了有{\rm Min}(N, D) -策略的M/G/1排队系统,文献[27]在文献[26]的基础上,把二维控制策略(N, D)与服务员的休假机制结合起来,构造了一个联合的{\rm Min}(N, D, V) -控制策略,使用全概率分解技术和利用拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布和稳态队长分布,同时,给出了稳态队长的随机分解结果和附加队长分布的显示表达式.最后在建立费用模型的基础上讨论了二维最优控制策略,并与单一的控制策略进行了比较分析.文献[28]讨论了基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统. ...
... ]在文献[26]的基础上,把二维控制策略(N, D)与服务员的休假机制结合起来,构造了一个联合的{\rm Min}(N, D, V) -控制策略,使用全概率分解技术和利用拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布和稳态队长分布,同时,给出了稳态队长的随机分解结果和附加队长分布的显示表达式.最后在建立费用模型的基础上讨论了二维最优控制策略,并与单一的控制策略进行了比较分析.文献[28]讨论了基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统. ...
具有{\rm Min}(N, D, V) -策略控制的M/G/1排队系统
4
2019
... 随着学者们对排队系统研究的深入和实际应用的需要,近几十年来在对有休假机制和控制策略的排队系统研究方面取得了较大的进展.早期的经典工作有Yadin和Naor的N -策略[1], Balachandran的D -策略[2], Yechiali和Heyman的T -策略[3], Doshi的休假排队系统[4]等.从已有的研究情况看,各个经典控制策略和休假机制都是从不同的角度提出的,其目的就是在平衡顾客等待时间的同时降低系统的成本,增加系统的收入.在一些经典工作之后,一些推广研究文献陆续出现[5-15].考虑到单一策略有各自的优缺点,例如,当生产制造环境发生改变并且系统拥有者想转换成另一种控制策略时,在这种情况下抛弃现有的硬件系统是不现实的,从而联合控制策略就是一种可供选择的好方案,能更好地解决这一实际问题.因此,结合实际背景,一些作者提出了一些具有联合控制策略的排队系统模型[16-28].文献[24]建立了有{\rm Min}(N, D) -策略控制的M/G/1排队模型,文献[25]在文献[24]的基础上,把到达过程推广到马尔科夫过程,分析了有{\rm Min}(N, D) -策略控制的MAP/G/1排队系统,文献[26]进一步讨论了有{\rm Min}(N, D) -策略的M/G/1排队系统,文献[27]在文献[26]的基础上,把二维控制策略(N, D)与服务员的休假机制结合起来,构造了一个联合的{\rm Min}(N, D, V) -控制策略,使用全概率分解技术和利用拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布和稳态队长分布,同时,给出了稳态队长的随机分解结果和附加队长分布的显示表达式.最后在建立费用模型的基础上讨论了二维最优控制策略,并与单一的控制策略进行了比较分析.文献[28]讨论了基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统. ...
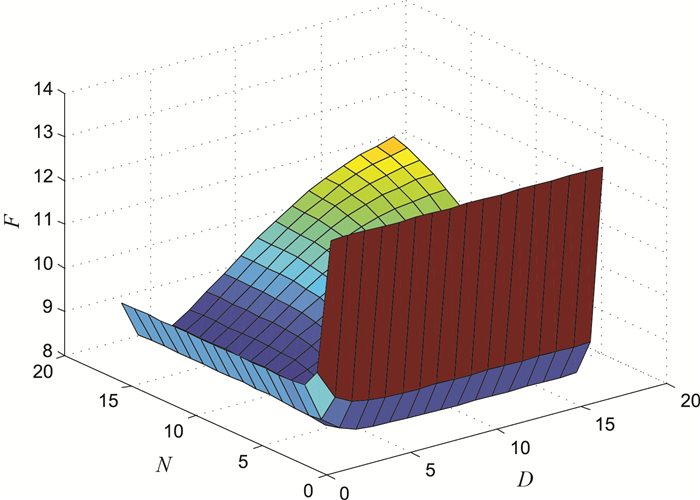
... 在诸多研究排队系统的文献中,作者都假定顾客的输入率是不变的,但实际上,到达的顾客可能因为服务员不在岗而离去,或者系统管理者为了控制在下一个忙期开始时系统中的顾客总数以免形成拥挤而要采取限制进入措施.文献[29]首次讨论了休假期间顾客以概率p(0 <p\leq 1)进入系统的多重休假M/G/1排队系统.文献[30]讨论了假期顾客以概率p(0\leq p\leq 1)进入系统的单重休假M/G/1排队,之后一些具有可变到达率的排队系统得到了研究[31-32],同时,一些离散时间刻画的且有可变进入率的离散时间排队系统研究也取得了进展[33-37].本文在文献[27]的基础上,将"休假期间顾客以概率p进入系统"引入到多重休假的{\rm Min}(N, D, V) -策略M/G/1排队中,建立"具有p进入规则和多重休假的{\rm Min}(N, D, V) -策略M/G/1排队模型",运用全概率分解技术和拉普拉斯变换工具讨论了系统的瞬态队长和稳态队长分布.结合获得的稳态队长分布,并通过数值计算实例讨论了系统容量的优化设计问题.最后,建立费用模型,讨论了系统长期单位时间内的期望费用达到最小的最优二维控制策略.本文研究的系统模型描述如下: ...
... 注3.1 当p=1时,本文研究的排队系统等价于文献[27]研究的排队系统,在上述所得结论中,令p=1,可得与文献[27]完全一致的结果. ...
... ,可得与文献[27]完全一致的结果. ...
具有{\rm Min}(N, D, V) -策略控制的M/G/1排队系统
4
2019
... 随着学者们对排队系统研究的深入和实际应用的需要,近几十年来在对有休假机制和控制策略的排队系统研究方面取得了较大的进展.早期的经典工作有Yadin和Naor的N -策略[1], Balachandran的D -策略[2], Yechiali和Heyman的T -策略[3], Doshi的休假排队系统[4]等.从已有的研究情况看,各个经典控制策略和休假机制都是从不同的角度提出的,其目的就是在平衡顾客等待时间的同时降低系统的成本,增加系统的收入.在一些经典工作之后,一些推广研究文献陆续出现[5-15].考虑到单一策略有各自的优缺点,例如,当生产制造环境发生改变并且系统拥有者想转换成另一种控制策略时,在这种情况下抛弃现有的硬件系统是不现实的,从而联合控制策略就是一种可供选择的好方案,能更好地解决这一实际问题.因此,结合实际背景,一些作者提出了一些具有联合控制策略的排队系统模型[16-28].文献[24]建立了有{\rm Min}(N, D) -策略控制的M/G/1排队模型,文献[25]在文献[24]的基础上,把到达过程推广到马尔科夫过程,分析了有{\rm Min}(N, D) -策略控制的MAP/G/1排队系统,文献[26]进一步讨论了有{\rm Min}(N, D) -策略的M/G/1排队系统,文献[27]在文献[26]的基础上,把二维控制策略(N, D)与服务员的休假机制结合起来,构造了一个联合的{\rm Min}(N, D, V) -控制策略,使用全概率分解技术和利用拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布和稳态队长分布,同时,给出了稳态队长的随机分解结果和附加队长分布的显示表达式.最后在建立费用模型的基础上讨论了二维最优控制策略,并与单一的控制策略进行了比较分析.文献[28]讨论了基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统. ...
... 在诸多研究排队系统的文献中,作者都假定顾客的输入率是不变的,但实际上,到达的顾客可能因为服务员不在岗而离去,或者系统管理者为了控制在下一个忙期开始时系统中的顾客总数以免形成拥挤而要采取限制进入措施.文献[29]首次讨论了休假期间顾客以概率p(0 <p\leq 1)进入系统的多重休假M/G/1排队系统.文献[30]讨论了假期顾客以概率p(0\leq p\leq 1)进入系统的单重休假M/G/1排队,之后一些具有可变到达率的排队系统得到了研究[31-32],同时,一些离散时间刻画的且有可变进入率的离散时间排队系统研究也取得了进展[33-37].本文在文献[27]的基础上,将"休假期间顾客以概率p进入系统"引入到多重休假的{\rm Min}(N, D, V) -策略M/G/1排队中,建立"具有p进入规则和多重休假的{\rm Min}(N, D, V) -策略M/G/1排队模型",运用全概率分解技术和拉普拉斯变换工具讨论了系统的瞬态队长和稳态队长分布.结合获得的稳态队长分布,并通过数值计算实例讨论了系统容量的优化设计问题.最后,建立费用模型,讨论了系统长期单位时间内的期望费用达到最小的最优二维控制策略.本文研究的系统模型描述如下: ...
... 注3.1 当p=1时,本文研究的排队系统等价于文献[27]研究的排队系统,在上述所得结论中,令p=1,可得与文献[27]完全一致的结果. ...
... ,可得与文献[27]完全一致的结果. ...
基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统的最优控制策略
2
2018
... 随着学者们对排队系统研究的深入和实际应用的需要,近几十年来在对有休假机制和控制策略的排队系统研究方面取得了较大的进展.早期的经典工作有Yadin和Naor的N -策略[1], Balachandran的D -策略[2], Yechiali和Heyman的T -策略[3], Doshi的休假排队系统[4]等.从已有的研究情况看,各个经典控制策略和休假机制都是从不同的角度提出的,其目的就是在平衡顾客等待时间的同时降低系统的成本,增加系统的收入.在一些经典工作之后,一些推广研究文献陆续出现[5-15].考虑到单一策略有各自的优缺点,例如,当生产制造环境发生改变并且系统拥有者想转换成另一种控制策略时,在这种情况下抛弃现有的硬件系统是不现实的,从而联合控制策略就是一种可供选择的好方案,能更好地解决这一实际问题.因此,结合实际背景,一些作者提出了一些具有联合控制策略的排队系统模型[16-28].文献[24]建立了有{\rm Min}(N, D) -策略控制的M/G/1排队模型,文献[25]在文献[24]的基础上,把到达过程推广到马尔科夫过程,分析了有{\rm Min}(N, D) -策略控制的MAP/G/1排队系统,文献[26]进一步讨论了有{\rm Min}(N, D) -策略的M/G/1排队系统,文献[27]在文献[26]的基础上,把二维控制策略(N, D)与服务员的休假机制结合起来,构造了一个联合的{\rm Min}(N, D, V) -控制策略,使用全概率分解技术和利用拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布和稳态队长分布,同时,给出了稳态队长的随机分解结果和附加队长分布的显示表达式.最后在建立费用模型的基础上讨论了二维最优控制策略,并与单一的控制策略进行了比较分析.文献[28]讨论了基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统. ...
... -控制策略,使用全概率分解技术和利用拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布和稳态队长分布,同时,给出了稳态队长的随机分解结果和附加队长分布的显示表达式.最后在建立费用模型的基础上讨论了二维最优控制策略,并与单一的控制策略进行了比较分析.文献[28]讨论了基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统. ...
基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统的最优控制策略
2
2018
... 随着学者们对排队系统研究的深入和实际应用的需要,近几十年来在对有休假机制和控制策略的排队系统研究方面取得了较大的进展.早期的经典工作有Yadin和Naor的N -策略[1], Balachandran的D -策略[2], Yechiali和Heyman的T -策略[3], Doshi的休假排队系统[4]等.从已有的研究情况看,各个经典控制策略和休假机制都是从不同的角度提出的,其目的就是在平衡顾客等待时间的同时降低系统的成本,增加系统的收入.在一些经典工作之后,一些推广研究文献陆续出现[5-15].考虑到单一策略有各自的优缺点,例如,当生产制造环境发生改变并且系统拥有者想转换成另一种控制策略时,在这种情况下抛弃现有的硬件系统是不现实的,从而联合控制策略就是一种可供选择的好方案,能更好地解决这一实际问题.因此,结合实际背景,一些作者提出了一些具有联合控制策略的排队系统模型[16-28].文献[24]建立了有{\rm Min}(N, D) -策略控制的M/G/1排队模型,文献[25]在文献[24]的基础上,把到达过程推广到马尔科夫过程,分析了有{\rm Min}(N, D) -策略控制的MAP/G/1排队系统,文献[26]进一步讨论了有{\rm Min}(N, D) -策略的M/G/1排队系统,文献[27]在文献[26]的基础上,把二维控制策略(N, D)与服务员的休假机制结合起来,构造了一个联合的{\rm Min}(N, D, V) -控制策略,使用全概率分解技术和利用拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布和稳态队长分布,同时,给出了稳态队长的随机分解结果和附加队长分布的显示表达式.最后在建立费用模型的基础上讨论了二维最优控制策略,并与单一的控制策略进行了比较分析.文献[28]讨论了基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统. ...
... -控制策略,使用全概率分解技术和利用拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布和稳态队长分布,同时,给出了稳态队长的随机分解结果和附加队长分布的显示表达式.最后在建立费用模型的基础上讨论了二维最优控制策略,并与单一的控制策略进行了比较分析.文献[28]讨论了基于{\rm Min}(N, D, V) -策略和单重休假的M/G/1排队系统. ...
服务员假期中以概率p进入的M/G/1排队系统的随机分解
2
2004
... 在诸多研究排队系统的文献中,作者都假定顾客的输入率是不变的,但实际上,到达的顾客可能因为服务员不在岗而离去,或者系统管理者为了控制在下一个忙期开始时系统中的顾客总数以免形成拥挤而要采取限制进入措施.文献[29]首次讨论了休假期间顾客以概率p(0 <p\leq 1)进入系统的多重休假M/G/1排队系统.文献[30]讨论了假期顾客以概率p(0\leq p\leq 1)进入系统的单重休假M/G/1排队,之后一些具有可变到达率的排队系统得到了研究[31-32],同时,一些离散时间刻画的且有可变进入率的离散时间排队系统研究也取得了进展[33-37].本文在文献[27]的基础上,将"休假期间顾客以概率p进入系统"引入到多重休假的{\rm Min}(N, D, V) -策略M/G/1排队中,建立"具有p进入规则和多重休假的{\rm Min}(N, D, V) -策略M/G/1排队模型",运用全概率分解技术和拉普拉斯变换工具讨论了系统的瞬态队长和稳态队长分布.结合获得的稳态队长分布,并通过数值计算实例讨论了系统容量的优化设计问题.最后,建立费用模型,讨论了系统长期单位时间内的期望费用达到最小的最优二维控制策略.本文研究的系统模型描述如下: ...
... 注2.1 当N=1或D=0时,本文研究的排队系统就是文献[29]讨论的在休假期内到达顾客以概率p进入系统的M/G/1多重休假排队系统,因此下面对N=1或D=0的情况不再讨论. ...
服务员假期中以概率p进入的M/G/1排队系统的随机分解
2
2004
... 在诸多研究排队系统的文献中,作者都假定顾客的输入率是不变的,但实际上,到达的顾客可能因为服务员不在岗而离去,或者系统管理者为了控制在下一个忙期开始时系统中的顾客总数以免形成拥挤而要采取限制进入措施.文献[29]首次讨论了休假期间顾客以概率p(0 <p\leq 1)进入系统的多重休假M/G/1排队系统.文献[30]讨论了假期顾客以概率p(0\leq p\leq 1)进入系统的单重休假M/G/1排队,之后一些具有可变到达率的排队系统得到了研究[31-32],同时,一些离散时间刻画的且有可变进入率的离散时间排队系统研究也取得了进展[33-37].本文在文献[27]的基础上,将"休假期间顾客以概率p进入系统"引入到多重休假的{\rm Min}(N, D, V) -策略M/G/1排队中,建立"具有p进入规则和多重休假的{\rm Min}(N, D, V) -策略M/G/1排队模型",运用全概率分解技术和拉普拉斯变换工具讨论了系统的瞬态队长和稳态队长分布.结合获得的稳态队长分布,并通过数值计算实例讨论了系统容量的优化设计问题.最后,建立费用模型,讨论了系统长期单位时间内的期望费用达到最小的最优二维控制策略.本文研究的系统模型描述如下: ...
... 注2.1 当N=1或D=0时,本文研究的排队系统就是文献[29]讨论的在休假期内到达顾客以概率p进入系统的M/G/1多重休假排队系统,因此下面对N=1或D=0的情况不再讨论. ...
假期中以概率p进入的单重休假M/G/1排队
1
2006
... 在诸多研究排队系统的文献中,作者都假定顾客的输入率是不变的,但实际上,到达的顾客可能因为服务员不在岗而离去,或者系统管理者为了控制在下一个忙期开始时系统中的顾客总数以免形成拥挤而要采取限制进入措施.文献[29]首次讨论了休假期间顾客以概率p(0 <p\leq 1)进入系统的多重休假M/G/1排队系统.文献[30]讨论了假期顾客以概率p(0\leq p\leq 1)进入系统的单重休假M/G/1排队,之后一些具有可变到达率的排队系统得到了研究[31-32],同时,一些离散时间刻画的且有可变进入率的离散时间排队系统研究也取得了进展[33-37].本文在文献[27]的基础上,将"休假期间顾客以概率p进入系统"引入到多重休假的{\rm Min}(N, D, V) -策略M/G/1排队中,建立"具有p进入规则和多重休假的{\rm Min}(N, D, V) -策略M/G/1排队模型",运用全概率分解技术和拉普拉斯变换工具讨论了系统的瞬态队长和稳态队长分布.结合获得的稳态队长分布,并通过数值计算实例讨论了系统容量的优化设计问题.最后,建立费用模型,讨论了系统长期单位时间内的期望费用达到最小的最优二维控制策略.本文研究的系统模型描述如下: ...
假期中以概率p进入的单重休假M/G/1排队
1
2006
... 在诸多研究排队系统的文献中,作者都假定顾客的输入率是不变的,但实际上,到达的顾客可能因为服务员不在岗而离去,或者系统管理者为了控制在下一个忙期开始时系统中的顾客总数以免形成拥挤而要采取限制进入措施.文献[29]首次讨论了休假期间顾客以概率p(0 <p\leq 1)进入系统的多重休假M/G/1排队系统.文献[30]讨论了假期顾客以概率p(0\leq p\leq 1)进入系统的单重休假M/G/1排队,之后一些具有可变到达率的排队系统得到了研究[31-32],同时,一些离散时间刻画的且有可变进入率的离散时间排队系统研究也取得了进展[33-37].本文在文献[27]的基础上,将"休假期间顾客以概率p进入系统"引入到多重休假的{\rm Min}(N, D, V) -策略M/G/1排队中,建立"具有p进入规则和多重休假的{\rm Min}(N, D, V) -策略M/G/1排队模型",运用全概率分解技术和拉普拉斯变换工具讨论了系统的瞬态队长和稳态队长分布.结合获得的稳态队长分布,并通过数值计算实例讨论了系统容量的优化设计问题.最后,建立费用模型,讨论了系统长期单位时间内的期望费用达到最小的最优二维控制策略.本文研究的系统模型描述如下: ...
在第二类故障期间以概率p进入的M/G/1可修排队系统
1
2012
... 在诸多研究排队系统的文献中,作者都假定顾客的输入率是不变的,但实际上,到达的顾客可能因为服务员不在岗而离去,或者系统管理者为了控制在下一个忙期开始时系统中的顾客总数以免形成拥挤而要采取限制进入措施.文献[29]首次讨论了休假期间顾客以概率p(0 <p\leq 1)进入系统的多重休假M/G/1排队系统.文献[30]讨论了假期顾客以概率p(0\leq p\leq 1)进入系统的单重休假M/G/1排队,之后一些具有可变到达率的排队系统得到了研究[31-32],同时,一些离散时间刻画的且有可变进入率的离散时间排队系统研究也取得了进展[33-37].本文在文献[27]的基础上,将"休假期间顾客以概率p进入系统"引入到多重休假的{\rm Min}(N, D, V) -策略M/G/1排队中,建立"具有p进入规则和多重休假的{\rm Min}(N, D, V) -策略M/G/1排队模型",运用全概率分解技术和拉普拉斯变换工具讨论了系统的瞬态队长和稳态队长分布.结合获得的稳态队长分布,并通过数值计算实例讨论了系统容量的优化设计问题.最后,建立费用模型,讨论了系统长期单位时间内的期望费用达到最小的最优二维控制策略.本文研究的系统模型描述如下: ...
在第二类故障期间以概率p进入的M/G/1可修排队系统
1
2012
... 在诸多研究排队系统的文献中,作者都假定顾客的输入率是不变的,但实际上,到达的顾客可能因为服务员不在岗而离去,或者系统管理者为了控制在下一个忙期开始时系统中的顾客总数以免形成拥挤而要采取限制进入措施.文献[29]首次讨论了休假期间顾客以概率p(0 <p\leq 1)进入系统的多重休假M/G/1排队系统.文献[30]讨论了假期顾客以概率p(0\leq p\leq 1)进入系统的单重休假M/G/1排队,之后一些具有可变到达率的排队系统得到了研究[31-32],同时,一些离散时间刻画的且有可变进入率的离散时间排队系统研究也取得了进展[33-37].本文在文献[27]的基础上,将"休假期间顾客以概率p进入系统"引入到多重休假的{\rm Min}(N, D, V) -策略M/G/1排队中,建立"具有p进入规则和多重休假的{\rm Min}(N, D, V) -策略M/G/1排队模型",运用全概率分解技术和拉普拉斯变换工具讨论了系统的瞬态队长和稳态队长分布.结合获得的稳态队长分布,并通过数值计算实例讨论了系统容量的优化设计问题.最后,建立费用模型,讨论了系统长期单位时间内的期望费用达到最小的最优二维控制策略.本文研究的系统模型描述如下: ...
多重假期中以概率p进入的M/G/1可修排队系统
1
2011
... 在诸多研究排队系统的文献中,作者都假定顾客的输入率是不变的,但实际上,到达的顾客可能因为服务员不在岗而离去,或者系统管理者为了控制在下一个忙期开始时系统中的顾客总数以免形成拥挤而要采取限制进入措施.文献[29]首次讨论了休假期间顾客以概率p(0 <p\leq 1)进入系统的多重休假M/G/1排队系统.文献[30]讨论了假期顾客以概率p(0\leq p\leq 1)进入系统的单重休假M/G/1排队,之后一些具有可变到达率的排队系统得到了研究[31-32],同时,一些离散时间刻画的且有可变进入率的离散时间排队系统研究也取得了进展[33-37].本文在文献[27]的基础上,将"休假期间顾客以概率p进入系统"引入到多重休假的{\rm Min}(N, D, V) -策略M/G/1排队中,建立"具有p进入规则和多重休假的{\rm Min}(N, D, V) -策略M/G/1排队模型",运用全概率分解技术和拉普拉斯变换工具讨论了系统的瞬态队长和稳态队长分布.结合获得的稳态队长分布,并通过数值计算实例讨论了系统容量的优化设计问题.最后,建立费用模型,讨论了系统长期单位时间内的期望费用达到最小的最优二维控制策略.本文研究的系统模型描述如下: ...
多重假期中以概率p进入的M/G/1可修排队系统
1
2011
... 在诸多研究排队系统的文献中,作者都假定顾客的输入率是不变的,但实际上,到达的顾客可能因为服务员不在岗而离去,或者系统管理者为了控制在下一个忙期开始时系统中的顾客总数以免形成拥挤而要采取限制进入措施.文献[29]首次讨论了休假期间顾客以概率p(0 <p\leq 1)进入系统的多重休假M/G/1排队系统.文献[30]讨论了假期顾客以概率p(0\leq p\leq 1)进入系统的单重休假M/G/1排队,之后一些具有可变到达率的排队系统得到了研究[31-32],同时,一些离散时间刻画的且有可变进入率的离散时间排队系统研究也取得了进展[33-37].本文在文献[27]的基础上,将"休假期间顾客以概率p进入系统"引入到多重休假的{\rm Min}(N, D, V) -策略M/G/1排队中,建立"具有p进入规则和多重休假的{\rm Min}(N, D, V) -策略M/G/1排队模型",运用全概率分解技术和拉普拉斯变换工具讨论了系统的瞬态队长和稳态队长分布.结合获得的稳态队长分布,并通过数值计算实例讨论了系统容量的优化设计问题.最后,建立费用模型,讨论了系统长期单位时间内的期望费用达到最小的最优二维控制策略.本文研究的系统模型描述如下: ...
具有可变到达率的多重休假Geo^{\lambda_1, \lambda_2}/G/1排队分析
1
2010
... 在诸多研究排队系统的文献中,作者都假定顾客的输入率是不变的,但实际上,到达的顾客可能因为服务员不在岗而离去,或者系统管理者为了控制在下一个忙期开始时系统中的顾客总数以免形成拥挤而要采取限制进入措施.文献[29]首次讨论了休假期间顾客以概率p(0 <p\leq 1)进入系统的多重休假M/G/1排队系统.文献[30]讨论了假期顾客以概率p(0\leq p\leq 1)进入系统的单重休假M/G/1排队,之后一些具有可变到达率的排队系统得到了研究[31-32],同时,一些离散时间刻画的且有可变进入率的离散时间排队系统研究也取得了进展[33-37].本文在文献[27]的基础上,将"休假期间顾客以概率p进入系统"引入到多重休假的{\rm Min}(N, D, V) -策略M/G/1排队中,建立"具有p进入规则和多重休假的{\rm Min}(N, D, V) -策略M/G/1排队模型",运用全概率分解技术和拉普拉斯变换工具讨论了系统的瞬态队长和稳态队长分布.结合获得的稳态队长分布,并通过数值计算实例讨论了系统容量的优化设计问题.最后,建立费用模型,讨论了系统长期单位时间内的期望费用达到最小的最优二维控制策略.本文研究的系统模型描述如下: ...
具有可变到达率的多重休假Geo^{\lambda_1, \lambda_2}/G/1排队分析
1
2010
... 在诸多研究排队系统的文献中,作者都假定顾客的输入率是不变的,但实际上,到达的顾客可能因为服务员不在岗而离去,或者系统管理者为了控制在下一个忙期开始时系统中的顾客总数以免形成拥挤而要采取限制进入措施.文献[29]首次讨论了休假期间顾客以概率p(0 <p\leq 1)进入系统的多重休假M/G/1排队系统.文献[30]讨论了假期顾客以概率p(0\leq p\leq 1)进入系统的单重休假M/G/1排队,之后一些具有可变到达率的排队系统得到了研究[31-32],同时,一些离散时间刻画的且有可变进入率的离散时间排队系统研究也取得了进展[33-37].本文在文献[27]的基础上,将"休假期间顾客以概率p进入系统"引入到多重休假的{\rm Min}(N, D, V) -策略M/G/1排队中,建立"具有p进入规则和多重休假的{\rm Min}(N, D, V) -策略M/G/1排队模型",运用全概率分解技术和拉普拉斯变换工具讨论了系统的瞬态队长和稳态队长分布.结合获得的稳态队长分布,并通过数值计算实例讨论了系统容量的优化设计问题.最后,建立费用模型,讨论了系统长期单位时间内的期望费用达到最小的最优二维控制策略.本文研究的系统模型描述如下: ...
Recursive solution of queue length distribution for Geo/G/1 queue with single server vacation and variable input rate
0
2011
Queue size distribution and capacity optimum design for N-policy Geo^{\lambda_1, \lambda_2, \lambda_3}/G/1 queue with setup time and variable input rate
0
2013
Optimal (r, N) -policy for discrete-time Geo/G/1 queue with different input rate and setup time
0
2015
Analysis of a discrete-time Geo^{\lambda_1, \lambda_2}/G/1 queue with N-policy and D-policy
1
2017
... 在诸多研究排队系统的文献中,作者都假定顾客的输入率是不变的,但实际上,到达的顾客可能因为服务员不在岗而离去,或者系统管理者为了控制在下一个忙期开始时系统中的顾客总数以免形成拥挤而要采取限制进入措施.文献[29]首次讨论了休假期间顾客以概率p(0 <p\leq 1)进入系统的多重休假M/G/1排队系统.文献[30]讨论了假期顾客以概率p(0\leq p\leq 1)进入系统的单重休假M/G/1排队,之后一些具有可变到达率的排队系统得到了研究[31-32],同时,一些离散时间刻画的且有可变进入率的离散时间排队系统研究也取得了进展[33-37].本文在文献[27]的基础上,将"休假期间顾客以概率p进入系统"引入到多重休假的{\rm Min}(N, D, V) -策略M/G/1排队中,建立"具有p进入规则和多重休假的{\rm Min}(N, D, V) -策略M/G/1排队模型",运用全概率分解技术和拉普拉斯变换工具讨论了系统的瞬态队长和稳态队长分布.结合获得的稳态队长分布,并通过数值计算实例讨论了系统容量的优化设计问题.最后,建立费用模型,讨论了系统长期单位时间内的期望费用达到最小的最优二维控制策略.本文研究的系统模型描述如下: ...
3
2006
... 又定义"服务员忙期"为从服务员开始为顾客服务的时刻起,直到系统再次变空为止的这一段时间,则本文定义的"服务员忙期"与文献[38,第4.4节]的"忙期"等价.令b表示该系统从一个顾客开始的"服务员忙期"长度,且令B(t)=p\{b\leq t\}, \ b(s)=\int_{0}^{\infty}{\rm e}^{-st}{\rm d}B(t),则有如下引理: ...
... 引理2.1[38] 对\Re(s)>0, b(s)是方程z=g(s+\lambda-\lambda z)在|z| < 1内的唯一根,且 ...
... 引理2.2[38] 令q^{*}_{j}(s)=\int_{0}^{\infty}{\rm e}^{-st}Q_{j}(t){\rm d}t为Q_{j}(t)的L变换,对\Re(s)>0, j\geq 1,有 ...
3
2006
... 又定义"服务员忙期"为从服务员开始为顾客服务的时刻起,直到系统再次变空为止的这一段时间,则本文定义的"服务员忙期"与文献[38,第4.4节]的"忙期"等价.令b表示该系统从一个顾客开始的"服务员忙期"长度,且令B(t)=p\{b\leq t\}, \ b(s)=\int_{0}^{\infty}{\rm e}^{-st}{\rm d}B(t),则有如下引理: ...
... 引理2.1[38] 对\Re(s)>0, b(s)是方程z=g(s+\lambda-\lambda z)在|z| < 1内的唯一根,且 ...
... 引理2.2[38] 令q^{*}_{j}(s)=\int_{0}^{\infty}{\rm e}^{-st}Q_{j}(t){\rm d}t为Q_{j}(t)的L变换,对\Re(s)>0, j\geq 1,有 ...