1 引言
其中
其中
2 预备知识
下面给出一些基本定义、引理及定理.为方便起见给出以下记号
(1)
(2) 对于一个在
(3) 如果
假设
的解,其中
定理2.1[15](存在唯一性定理) 假设
(1) 局部Lipschitz条件:存在
成立;
(2) 线性增长条件:存在
则初始条件为
定理2.2[15] (
其中
定理2.3[15](随机微分方程比较定理) 设
的解,其中
(1) 存在定义在
(2)
(3)
则有
定义2.1[9] 设
(1) 若
(2) 若
考虑下列随机微分方程
引理2.1[9] 设
考虑下列随机微分方程
其中
引理2.2[9]
和
设
其扩散矩阵为
作如下假设:
(A) 存在具有正则边界
(A1) 在
(A2) 当
为了验证(A1)成立,我们只需证明
为了验证(A2)成立,只要证明存在非负的
下面,考虑如下方程
假设方程(2.4)的系数
其中
则方程(2.4)存在一个
3 主要结果
定理3.1 对任意给定的初值
证 首先考虑如下方程
显然,系统
令
定义
假设
定义一个
其中
同理可得
即
事实上,由于
关于
下面的证明与文献[17]的相似,所以省略.
定理3.2 设
证 由文献[7]可以得到,种群
因为
现在证明种群
对上述不等式两边同时从0到
两边同时除以
根据引理2.2和随机微分方程的比较定理,可得
所以,当
所以,当
定理3.3 设
(i) 若
(ii) 若
(iii) 若
证 (i)由系统(3.1)可得
由条件(i)和引理2.1有
即
即对于任意的
可得
又由于
由于
所以,当
(ii) 从系统(3.1)可得
与方程(3.2)的证明类似,当
类似的,对于任意的
当
由于
所以,当
(iii) 当
即,当
定理3.4 设系统(1.1)满足
证 定义
其中
其中
其中
所以
选择足够小的
下面,考虑有界集
假设
显然,
下面证明,对于任意的
当
当
当
当
从上述的讨论可知:对任意的
此外,可以找到一个常数
因此条件(A1)也满足.所以系统(1.1)存在平稳分布,且具有遍历性.
定理3.5 若
证 构造
其中
由
所以,
显然,当
这就验证了方程(2.6)的条件(1).下面只需验证方程(2.6)条件(2).假设
对
其中
同理可得
其中
所以有
因为
又因为
所以
其中
选择足够小的
考虑有界集
假设
显然,
下面的证明与定理3.4的证明类似,所以省略.
4 数值模拟与结论
文章研究了白噪声扰动下的随机捕食-食饵系统.利用随机分析的方法,证明了系统(1.1)对于任意的正初始值,存在唯一的全局正解;平均意义下的持久性;使用Has'minskii的平稳分布理论及周期性理论得到了系统(1.1)满足一定条件,存在平稳分布并且是遍历的,这些条件反映了大幅度环境噪声可能会使系统变得不稳定;进而证明了对于任意的正初始值,系统(1.2)存在正周期解.
为了验证理论结果,采用Milstein高阶方法[18]对随机系统(1.1)和(1.2)进行数值模拟.
对于系统(1.1),取
图 1
图 1
左侧是系统(1.1)的密度函数图,右侧是系统(1.1)的解与其确定性系统的解.这里
对于系统(1.1),取
图 2
图 2
左侧是系统(1.1)的密度函数图,右侧是系统(1.1)的解与其确定性系统的解.这里
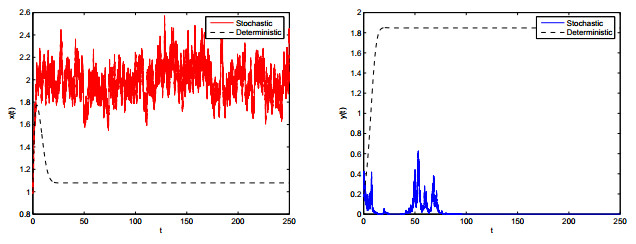
对于系统(1.1),取
图 3
图 3
系统(1.1)的解与其确定性系统的解.这里
对于系统(1.1),取
图 4
图 4
系统(1.1)的解与其确定性系统的解.这里
对于系统(1.1),取
图 5
图 5
系统(1.1)的解与其确定性系统的解.这里
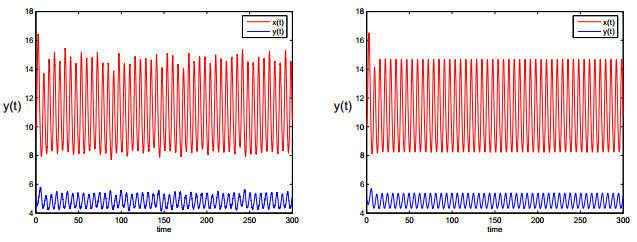
对于系统(1.2),取
图 6
图 6
左侧是系统(1.2)的解,右侧是相应的确定系统的解,这里
图 7
图 7
左侧为系统(1.2)的相轨线,右侧为相应的确定系统的相轨线.这里
参考文献
A stochastic SIRS epidemic model with nonlinear incidence rate
Dynamical behavior of a stochastic HBV infection model with logistic hepatocyte growth
一类具有校正隔离率随机SIQS模型的绝灭性与分布
Extinction and distribution for an SIQS epidemi model with quarantined-adjusted incidence
Periodic behavior in a FIV model with seasonality as well as environment fluctuations
DOI:10.1016/j.jfranklin.2017.08.034 [本文引用: 2]
Dynamical behavior of a one-prey two-predator model with random perturbations
A note on a predator-prey model with modified Leslie-Gower and Holling-type Ⅱ schemes with stochastic perturbation
DOI:10.1016/j.jmaa.2010.11.008
Stochastic persistence and stationary distribution in a Holling-Tanner type prey-predator model
DOI:10.1016/j.physa.2011.10.019 [本文引用: 1]
Stationary distribution and periodic solutions for stochastic Holling-Leslie predator-prey systems
DOI:10.1016/j.physa.2016.04.037 [本文引用: 1]
Analysis of a predator-prey model with modified Leslie-Gower and Holling-type Ⅱ schemes with stochastic perturbation
DOI:10.1016/j.jmaa.2009.05.039 [本文引用: 3]
Dynamics of the stochastic Leslie-Gower predator-prey system with randomized intrinsic growth rate
DOI:10.1016/j.physa.2016.06.010
Analysis of a stochastic two-predators one-prey system with modified Leslie-Gower and Holling-type Ⅱ schemes
Dynamics of a two-prey one-predator system in random environments
Dynamics of a stochastic predator-prey system with BeddingtonDeAngelis functional response
Persistence, extinction and global asymptotical stability of a non-autonomous predatorprey model with random perturbation
DOI:10.1016/j.apm.2011.12.057 [本文引用: 1]
Environmental Brownian noise suppresses explosions in population dynamics
DOI:10.1016/S0304-4149(01)00126-0 [本文引用: 1]