波谱学杂志, 2024, 41(3): 331-340 doi: 10.11938/cjmr20243089

研究论文

氦气渗透导致铷原子钟频率漂移的计算与分析

李豆1,2, 王鹏飞1, 钟达1, 梅刚华1, 康松柏,1,*

1.中国科学院原子频标重点实验室（中国科学院精密测量科学与技术创新研究院），湖北 武汉 430071

2.中国科学院大学，北京 100049

Calculation and Analysis of Helium-permeation-induced Frequency Drift of the Rubidium Atomic Clock

LI Dou1,2, WANG Pengfei1, ZHONG Da1, MEI Ganghua1, Kang Songbai,1,*

1. CAS Key Laboratory of Atomic Frequency Standards (Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences), Wuhan 430071, China

2. University of Chinese Academy of Sciences, Beijing 100049, China

通讯作者: *Tel: 15871777484, E-mail:kangsongbai@apm.ac.cn.

收稿日期: 2023-11-1  

基金资助: 国家自然科学基金资助项目(12173064)

Corresponding authors: *Tel: 15871777484, E-mail:kangsongbai@apm.ac.cn.

Received: 2023-11-1  

摘要

氦气渗透导致的铷原子钟吸收泡内铷原子与氦气碰撞频移发生变化,从而影响铷原子钟频率漂移率．为了量化分析这一影响，选取厚度为1 mm，直径为1.8 cm，长为1.6 cm，工作温度为65 ℃的圆柱型玻璃气泡为例，通过数值方法模拟了派热克斯玻璃（Pyrex，康宁7740）与低氦渗透的铝硅酸盐玻璃（ASG，康宁1720）原子气泡内氦气压随时间的变化规律．计算结果显示，对于Pyrex气泡，铷原子钟工作约12年后，氦渗透致频率漂移率降低至<1.0×10-14/天；而ASG气泡铷原子钟在其寿命期间内的氦渗透致频率漂移率始终<3.0×10-17/天，其对铷原子钟漂移率的贡献可忽略不计．该计算方法同样适用于其它种类气体在不同玻璃材料的渗透过程研究．

关键词： 氦气渗透; 铷原子钟; 频率漂移; 原子气泡; 派热克斯玻璃; 铝硅酸盐玻璃

Abstract

Due to the collision-shift effect, helium permeation into the vapor cell causes a time-dependent frequency drift in rubidium atomic clock. To quantify this shift, a cylindrical vapor cell with dimensions of 1.8 cm in diameter, 1.6 cm in height, and 1 mm in thickness, operating at a temperature of 65 ℃, is selected for analysis. Numerical methods are employed to simulate the temporal variation of helium gas pressure within atomic vapor cells composed of Pyrex (Corning 7740) and low helium-permeable aluminosilicate (Corning 1720). The results of the calculations indicate that for Pyrex vapor cells, after 12 years of operation, the drift rate attributable to helium permeation decreases to less than 1.0×10-14/day. In contrast, the frequency drift rate due to helium permeation in aluminosilicate vapor cell rubidium atomical clocks remains below 3.0×10-17/day throughout their operational lifetime, rendering its contribution to the drift rate negligible. This computational approach is also applicable to the investigation of the permeation processes of other gaseous species in various glass materials.

Keywords： helium permeation; rubidium atomic clock; frequency drift; vapor cell; Pyrex; aluminosilicate

PDF (721KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

李豆, 王鹏飞, 钟达, 梅刚华, 康松柏. 氦气渗透导致铷原子钟频率漂移的计算与分析[J]. 波谱学杂志, 2024, 41(3): 331-340 doi:10.11938/cjmr20243089

LI Dou, WANG Pengfei, ZHONG Da, MEI Ganghua, Kang Songbai. Calculation and Analysis of Helium-permeation-induced Frequency Drift of the Rubidium Atomic Clock[J]. Chinese Journal of Magnetic Resonance, 2024, 41(3): 331-340 doi:10.11938/cjmr20243089

引言

气泡型铷原子钟因其频率稳定度好、体积小、功耗低以及良好的空间环境适应性等特点，被广泛应用于卫星导航等领域[1,2].目前高性能的铷原子钟稳定度已经优于铯原子钟、接近氢原子钟[3]，但由于存在较大的频率漂移率（~1×10-13/天），因此限制了其自主守时运行能力[4].其中，导致铷原子钟漂移的物理机理之一就是气体渗穿过原子泡壁后与吸收泡内铷原子间的碰撞频移.而氦气在玻璃材料中的物理渗透最快[5,6]，且与铷原子的碰撞频移系数较大[7]，因此主要关注的是氦气渗透对铷原子钟频率漂移的影响[8].由于氦渗透过程通常十分缓慢，对氦气渗透导致的铷原子钟频率漂移量进行精密测量的难度大，因此精确求解氦渗透过程中铷气泡内氦气压变化对研究铷原子钟漂移产生机理及其漂移率的评估具有指导意义.

目前关于封闭气泡内的氦渗透理论计算研究是基于气泡内氦气压可忽略的假设前提，即仅适用于氦气渗透进入气泡的初期[9⇓⇓⇓⇓-14].例如文献[9]在泡内氦气压可忽略的情形下，从扩散方程出发得到了初期气泡内氦气压变化的近似解析解，结果显示气泡内氦气压随时间线性增加.该近似解被文献[10⇓⇓⇓-14]用于原子气泡氦渗透实验数据拟合和分析.另外，还有氦渗透实验与理论研究利用稳态近似[15]，即假设气泡壁内氦气浓度沿渗透方向线性变化，得到了泡内氦气压随时间呈以自然对数为底的指数变化规律.文献[16⇓⇓⇓⇓⇓⇓-23]对氦渗透致气泡型原子钟的频率漂移、氦渗透对真空度的破坏、氦气渗透出入玻璃材料过程中的分析和数据处理参考了该稳态近似解.而实际上，氦气的流密度和玻璃内侧处的氦气浓度梯度有关而并非线性.此外，稳态近似解虽能描述初始状态与平衡状态，但其边界条件也只在气泡内氦气压可被忽略时成立.本工作将从从扩散方程出发，结合玻璃内侧氦气浓度变化的边界条件，对原子气泡内氦气压变化规律进行数值求解.

本文以铷原子钟常用的圆柱形Pyrex玻璃（康宁7740）气泡和ASG玻璃（康宁1720）气泡为例计算氦气在气泡中的渗透过程.氦渗透到原子气泡内的过程分为两个阶段，阶段一为氦气在气泡玻璃壁内的渗透，即氦气渗透进入泡壁一侧（外侧）直到刚好抵达泡壁另一侧（内侧），此时玻璃内氦气浓度梯度为定值，称为恒流过程；阶段二为氦气在气泡内的累积，即氦气从泡壁另一侧（内侧）进入气泡内部空间直到气泡内氦气压与气泡外氦分压相等，称为氦累积过程.本文分析计算的重点围绕阶段二展开，利用不同定解条件下的扩散方程来进行求解.文章第二部分给出了圆柱形气泡的等效模型以及计算过程所需要的近似条件，并介绍了文献[9]中给出的恒流过程的解；第三部分详细求解了氦累积过程的扩散方程，得到了气泡内氦气压及氦气压变化率随时间变化的数值解，并与稳态近似解进行对比分析；第四部分利用计算结果分析评估了氦渗透对铷原子钟频率漂移率的影响.

1 等效模型与恒流过程

1.1 等效模型

本文计算以圆柱形铷吸收泡（图1）为例，假设铷泡厚度为a且各处均匀，内体积为V，外表面积为A，工作温度恒为T，气泡外氦气压始终为P1，初始时刻气泡玻璃内和气泡内部空间的氦浓度均为0.尺寸参数值及相关常数见表1.

图1

新窗口打开| 下载原图ZIP| 生成PPT

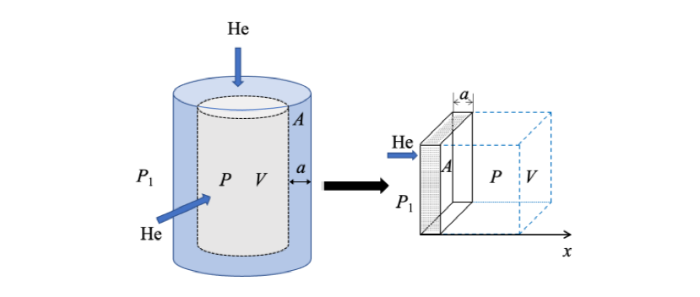
图1   圆柱形气泡中的氦渗透等效过程示意图

Fig. 1   Schematic diagram of the equivalent process of helium permeation through a cylindrical vapor cell


表1   圆柱形铷泡尺寸及相关常数

Table 1  Dimension of cylindrical Rb vapor cell and related constants

参数含义数值单位
A外表面积14.13cm2
a玻璃厚度0.1cm
V内体积2.8cm3
T工作温度338.15K
T0标准温度273.15K
KB玻尔兹曼常数1.38×10-23J•K-1
P1外界氦气压3.98mTorr

新窗口打开| 下载CSV


氦气从外界渗透进入玻璃气泡内属于气体分子输运问题，可用扩散方程描述.文献[9]计算结果显示在恒流过程中，圆柱形气泡中的氦渗透问题可以用平板玻璃模型近似处理.

氦累积过程中，氦气进入气泡后由于分子热运动，会迅速均匀分布在气泡内空间各处，其速率远大于氦气在玻璃里的渗透速率，气泡内氦浓度均相等.与文献[9]指出的溶解规律类似，气泡玻璃内壁的氦浓度仅由其所处的气体环境氦气压决定，因此，任意时刻气泡内壁各处氦浓度均相等.又因为外界氦气压恒定，所以任意时刻气泡外壁的氦浓度也相等.如此一来，氦渗透问题的边界条件已经确立，且和形状无关.初始条件为恒流状态时玻璃内部各处的浓度分布，可等效为平板玻璃模型进行处理得到.

由上述分析可知，在研究气泡内氦气压$P(t)$随时间的变化规律时，整个氦渗透过程可以等效为在同样厚度、表面积与体积的平板玻璃中的渗透过程，如图1所示.此时渗透过程只发生在x轴正向，且只在等效平板玻璃的两个面进行，蓝色虚线部分为铷泡内部的等效体积.

1.2 恒流过程

由文献[9]可知，环境中的氦气迅速溶解到等效平板玻璃表面，此时左侧玻璃表面氦气浓度为 SP1/（KBT0），S为氦气在玻璃材料中的溶解率，KB为玻尔兹曼常数，T0为标准温度.玻璃内部氦初始浓度为0，随后氦气沿着x轴从左向右渗透进入平板玻璃直至刚好到达右侧玻璃壁，此时玻璃内各处氦浓度梯度相等，达到恒流状态.此后，氦气进入气泡内开始累积，当气泡内氦气压可以忽略时，一段时间内气泡内氦气压$P(t)$随时间变化表达式可近似为[9]：

$P(t)=\frac{ADS{{P}_{1}}T}{{{T}_{0}}Va}\left\{ t-\frac{{{a}^{2}}}{6D}-\frac{2{{a}^{2}}}{{{\text{ }\!\!\pi\!\!\text{ }}^{2}}D}\sum\limits_{n=1}^{\infty }{{{(-1)}^{n}}\frac{\exp (-{{n}^{2}}{{\text{ }\!\!\pi\!\!\text{ }}^{2}}Dt/{{a}^{2}})}{{{n}^{2}}}} \right\}$

其中，D为氦气在玻璃材料中的扩散系数.上式中的级数能迅速收敛，因此在t很大时，级数和为0，此时[9]，

$P(t)=\frac{ADS{{P}_{1}}T}{{{T}_{0}}Va}(t-{{t}_{\text{c}}})$
${{t}_{\text{c}}}=\frac{{{a}^{2}}}{6D}$

(2)式和(3)式中，${{t}_{\text{c}}}$为到达恒流状态所需的时间.

2 氦累积过程

$t={{t}_{\text{c}}}$时刻以后铷泡进入氦气累积阶段，恒流过程边界条件破坏，(1)式无法准确描述此后铷泡内氦气压随时间变化.铷泡内氦气压$P(t)$与相邻泡壁一侧浓度$u(a,t)$通过溶解规律与粒子数守恒以及理想气体状态方程联系起来.此时扩散方程的定解条件为：

$\frac{\partial u(x,t)}{\partial t}=D\frac{{{\partial }^{2}}u(x,t)}{\partial {{x}^{2}}}$
$u(0,t)=\frac{S{{P}_{1}}}{{{K}_{B}}{{T}_{0}}}$
$u(x,0)=-\frac{S{{P}_{1}}}{{{K}_{\text{B}}}{{T}_{0}}a}x+\frac{S{{P}_{1}}}{{{K}_{\text{B}}}{{T}_{0}}}$

气泡内氦气压$P(t)$与浓度${{u}_{\text{g}}}(t)$和平板玻璃$x=a$处氦浓度$u(a,t)$建立以下联系，

$u(a,t)=\frac{SP(t)}{{{K}_{\text{B}}}{{T}_{0}}}=\frac{S{{K}_{\text{B}}}T{{u}_{\text{g}}}(t)}{{{K}_{\text{B}}}{{T}_{0}}}=\frac{ST{{u}_{\text{g}}}(t)}{{{T}_{0}}}$
$V\frac{\text{d}{{u}_{\text{g}}}(t)}{\text{d}t}=-DA{{\left( \frac{\partial u(x,t)}{\partial x} \right)}_{x=a}}$

(7)式表示铷泡内氦气部分溶解在玻璃右侧且气泡内氦气压满足理想气体状态方程，(8)式可由玻璃右侧粒子数守恒对时间求导得到.边界齐次化：

$u(x,t)=v(x,t)+\frac{S{{P}_{1}}}{{{K}_{\text{B}}}{{T}_{0}}}$

代入到(4)~(8)式可得：

$\frac{\partial v(x,t)}{\partial t}=D\frac{{{\partial }^{2}}v(x,t)}{\partial {{x}^{2}}}$
$v(0,t)=0$
$v(x,0)=-\frac{S{{P}_{1}}}{{{K}_{\text{B}}}{{T}_{0}}a}x$
$v(a,t)=\frac{ST{{u}_{\text{g}}}(t)}{{{T}_{0}}}-\frac{S{{P}_{1}}}{{{K}_{\text{B}}}{{T}_{0}}}$
$\frac{\text{d}{{u}_{\text{g}}}(t)}{\text{d}t}=-\frac{DA}{V}{{\left( \frac{\partial v(x,t)}{\partial x} \right)}_{x=a}}$

其通解为：

$v(x,t)=c\sin (\omega x)\exp (-{{\omega }^{2}}Dt)$

其中，c为任意实数，$\omega$为分离变量法求通解过程中引入的任意大于0的实数.由于扩散方程与边界是线性齐次的，故其解为：

$v(x,t)=\sum\limits_{n}{{{c}_{n}}\sin ({{\omega }_{n}}x)\exp (-\omega _{n}^{2}}Dt)$

代入初始条件(12)式中得：

$\sum\limits_{n}{{{c}_{n}}}\sin ({{\omega }_{n}}x)=-\frac{S{{P}_{1}}}{a{{K}_{\text{B}}}{{T}_{0}}}x$

利用(13)式与(15)式可得：

$c\sin (\omega a)\exp (-{{\omega }^{2}}Dt)=-\frac{ST}{{{T}_{0}}}{{u}_{\text{g}}}(t)-\frac{S{{P}_{1}}}{{{K}_{\text{B}}}{{T}_{0}}}$

于是：

${{u}_{\text{g}}}(t)=\left[ c\sin (\omega a)\exp (-{{\omega }^{2}}Dt)+\frac{S{{P}_{1}}}{{{K}_{\text{B}}}{{T}_{0}}} \right]\frac{{{T}_{0}}}{ST}$

将上式对t求导得：

$\frac{\text{d}{{u}_{\text{g}}}(t)}{\text{d}t}=-{{\omega }^{2}}Dc\sin (\omega a)\exp (-{{\omega }^{2}}Dt)\frac{{{T}_{0}}}{ST}$

(15)式对x求偏导并令$x=a$有：

${{\frac{\partial v(x,t)}{\partial x}}_{(x=a)}}=c\omega \cos (\omega a)\exp (-{{\omega }^{2}}Dt)$

将(16)、(19)式代入到(14)式中有：

$\frac{-{{\omega }^{2}}Dc{{T}_{0}}}{ST}=\sin (\omega a)\exp (-{{\omega }^{2}}Dt)=\frac{-DAc\omega }{V}\cos (\omega a)\exp (-{{\omega }^{2}}Dt)$

得到：

$\text{tan}(\omega a)=\frac{ATS}{V{{T}_{0}}\omega }$

此式为关于$\omega$的超越方程，无解析解.为了获得吸收泡工作温度下溶解度S的具体数值，根据文献[12]中(3)式与相应参数可计算得到65 ℃时氦气在两种玻璃材料中的扩散系数，由于溶解度S与扩散系数D有类似的数学表达式，且在一定温度范围内S的变化明显缓慢于D，可由S=K/D以及文献[12]中渗透率K@20 ℃与K@500 ℃的具体数值，最后推算出65 ℃时氦气在Pyrex玻璃材料中的溶解度.代入表1中铷泡尺寸与相关常数的具体数值至(23)式，然后利用图解法求解，取前五个解，分别为：

${{\omega }_{1}}=0.55$
${{\omega }_{2}}=31.43$
${{\omega }_{3}}=62.84$
${{\omega }_{4}}=94.25$
${{\omega }_{5}}=125.67$

代入(17)式并利用斯密特正交化公式将$\sin ({{\omega }_{n}}x)$正交化，对(17)式右边-x进行傅里叶展开并与左边对应，得到${{c}_{n}}={{{c}'}_{n}}S{{P}_{1}}/(a{{K}_{\text{B}}}{{T}_{0}})$，${{{c}'}_{n}}$如下：

${{{c}'}_{1}}=-1.81$
${{{c}'}_{2}}=1.94\times {{10}^{-5}}$
${{{c}'}_{3}}=-2.31\times {{10}^{-6}}$
${{{c}'}_{4}}=6.25\times {{10}^{-7}}$
${{{c}'}_{5}}=-2.29\times {{10}^{-7}}$

可见(17)左式级数迅速收敛，因此5个根足够.由(9)式与(16)式知玻璃内氦浓度$u(x,t)$为：

$u(x,t)\approx \frac{S{{P}_{1}}}{{{K}_{\text{B}}}{{T}_{0}}}\left[ 1+\frac{1}{a}\sum\limits_{i=1}^{5}{{{{{c}'}}_{i}}}\sin ({{\omega }_{i}}x)\exp (-\omega _{i}^{2}Dt) \right]$

将上式代入(7)式，于是气泡内氦气压表达式为：

$P(t)={{u}_{\text{g}}}(t){{K}_{\text{B}}}T=u(a,t)\frac{{{K}_{\text{B}}}{{T}_{0}}}{S}\approx {{P}_{1}}\left[ 1+\frac{1}{a}\sum\limits_{i=1}^{5}{{{{{c}'}}_{i}}}\sin ({{\omega }_{i}}a)\exp (-\omega _{i}^{2}Dt) \right]$

(23)式的超越方程虽然无解析解且根有无数个，但由于单调性限制，$\omega a$的值近似以$\pi$为间隔相邻分布，考虑到气泡厚度，(23)式的解如数值求解给出的前5个解一样迅速变大，对应exp函数随时间衰减速度也迅速变快.当${{\omega }_{2}}$与${{\omega }_{1}}$差距较大时，${{\omega }_{2}}\tilde{\ }{{\omega }_{1}}$可近似表示为，

${{\omega }_{2}}-{{\omega }_{1}}\tilde{\ }\frac{\text{ }\!\!\pi\!\!\text{ }}{a}-\sqrt{\frac{ATS}{V{{T}_{0}}a}}$

(26)式在a越小时差越大，取$\sin {{\omega }_{1}}x\tilde{\ }{{\omega }_{1}}x$，此时(22)式近似为，

$v(x,t)={{c}_{1}}{{\omega }_{1}}x\exp (-\omega _{1}^{2}Dt)$

同理代入初始条件(12)式有，

$v(x,t)=-\frac{S{{P}_{1}}}{{{K}_{\text{B}}}{{T}_{0}}a}x\exp (-\omega _{1}^{2}Dt)$

由(13)式可知，

${{u}_{\text{g}}}(t)=\frac{{{P}_{1}}}{{{K}_{\text{B}}}T}\left[ 1-\exp (-\omega _{1}^{2}Dt) \right]$

由(23)式可知，

${{\omega }_{1}}\tilde{\ }\sqrt{\frac{ATS}{V{{T}_{0}}a}}$

于是气泡内氦气压随时间变化规律为，

$P(t)={{P}_{1}}\left[ 1-\exp \left( \frac{ATSD}{V{{T}_{0}}a}t \right) \right]$

代入$K=DS$并转换单位后，(31)式与文献[22]中稳态近似(1)、(2)式在初始时刻气泡内无氦气时一致.

将$\omega$与${c}'$以及D（表2）代入(25)式，并对其求时间t的导数，得到如图2(a)所示Pyrex气泡内氦气压及氦气压变化率随时间变化规律.利用表3中的数据，同理也能求出抗氦性能更好的ASG[21]气泡内氦气压及氦气压变化率随时间的变化规律，如图2(b)所示.图中的蓝色虚线为两种材料气泡内氦气压达到环境氦气压的99%所需要的时间，定义为平衡时间.从图2中可以看出，氦渗透是缓慢的过程，且渗透速率是逐渐减小的.开始时气泡内外氦浓度差最大，氦渗透速率也最大；随着气泡内的氦浓度逐渐变大，氦渗透速率逐渐减小，直至气泡内外氦浓度一致而停止渗透.另外，从(2)式可知渗透速率和溶解度与扩散系数乘积即渗透系数成正比，而由表2和表3可知，ASG玻璃和Pyrex玻璃的扩散系数相差4个数量级，溶解度差别不大.计算结果显示，同一时刻两种材料气泡的氦渗透速率也相差近4个数量级，因此导致了气泡内氦气压累积速率与平衡时间的显著差异.

图2

新窗口打开| 下载原图ZIP| 生成PPT

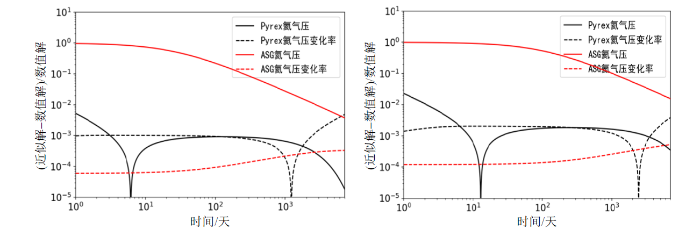
图2   Pyrex (a)和ASG (b)气泡中的氦气压及其变化率的变化规律图

Fig. 2   Helium pressure and its change rate in Pyrex (left) and ASG (right) vapor cell


表2   Pyrex气泡渗透过程相关参数

Table 2  Related parameters of helium permeation through Pyrex vapor cell

参数含义数值单位
S@65℃溶解度4.9×10-3cm3(STP)cm3
D@65℃扩散系数3.11×10-8cm2•s-1
D0[12]扩散常数4.6×10-4cm2•s-1
ED[12]扩散能-0.28eV
K@20 ℃[12]渗透率3.5×10-11cm2•s-1
K@500 ℃[12]渗透率3.4×10-8cm2•s-1

新窗口打开| 下载CSV


表3   ASG气泡渗透过程相关参数

Table 3  Related parameters of helium permeation through ASG vapor cell

参数含义数值单位
S@65℃溶解度1.6×103cm3(STP)cm3
D@65℃扩散系数6.7×10-12cm2•s-1
D0[12]扩散常数3.7×10-4cm2•s-1
ED[12]扩散能-0.52eV
K@20 ℃[12]渗透率6.8×10-16cm2•s-1
K@500 ℃[12]渗透率2.4×10-10cm2•s-1

新窗口打开| 下载CSV


为了对比稳态近似解与数值解，我们计算了稳态近似解相对于数值解的相对误差（近似解与数值解的差除以数值解），图3是其绝对值随时间的变化.可以看出对于Pyrex材料气泡而言，氦气压与氦气压变化率的相对误差均小于1%.对ASG材料气泡而言，初期氦气压相对误差较大，达到了100%，而氦气压变化率的相对误差则可以忽略.为了体现厚度对相对误差绝对值大小的影响同时兼顾实际情况考虑，给出了气泡玻璃厚度为2 mm时的相对误差绝对值随时间的变化规律，如图3右所示.可以看出尽管两种材料的氦气压变化率相对误差绝对值有所增大，但依旧均小于1%，Pyrex材料气泡的氦气压相对误差最大增大到2%左右，ASG材料气泡的氦气压相对误差则变化不明显，最大值依旧为100%.图中尖锋是由于数值解与稳态近似差值趋于零所致.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   厚度为1 mm（左）和2 mm（右）气泡内氦气压与氦气压变化率近似解相对于数值解的误差百分比随时间变化曲线

Fig. 3   The percentage error of the approximate solution of the helium pressure and its change rate with respect to the numerical solution varies with time for Pyrex and ASG vapor cell with a thickness of 1 mm (left) and 2 mm (right)


总的来看，相较1 mm厚的Pyrex玻璃气泡，当气泡玻璃厚度增加或者对氦溶解度减小时，稳态近似的相对误差将会增大.但就实际原子气泡尺寸与材料而言，稳态近似足以用于分析当前铷原子钟气泡里的氦渗透致频率漂移（和氦气压变化率成正比），其相对误差小于1%.

3 氦渗透对铷原子钟频率漂移的影响

基于表1、表2、表3的数据与(3)式可计算得出两种材料气泡对应的恒流时间分别为1天和8.8年，即Pyrex气泡工作约1天后开始累积氦气，而ASG气泡则需工作8.8年后才会开始累积.根据图2中的氦气压变化率，结合氦气导致铷原子钟产生碰撞频移的系数（约1.05×10-7/Torr）[25]，分别推算得出两种材料气泡中氦渗透致铷原子钟的频率漂移随时间变化规律曲线，如图4所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

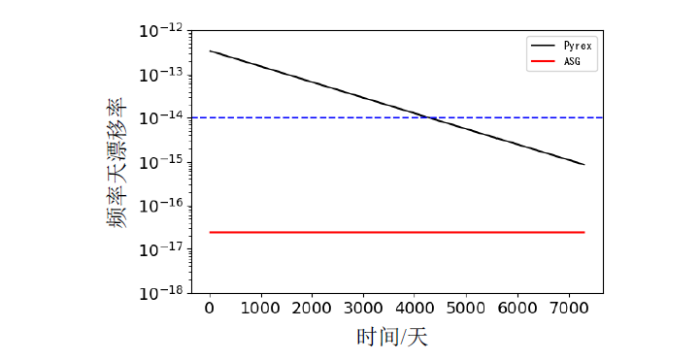
图4   Pyrex气泡与ASG气泡中氦渗透致铷钟频率漂移结果图

Fig. 4   Time-dependent frequency drift of Rubidium atomic clock due to helium permeation in Pyrex and Aluminosilicate glass vapor cell


在约10年时间尺度内，ASG气泡内的氦渗透致漂移率只变化了0.05%，而Pyrex气泡内的氦渗透致漂移率则变化了约一个数量级.图中虚线对应铷原子钟1×10-14/天的天漂移率，该漂移率值是目前报道的铷原子钟频率漂移率极限水平.图4的结果表明，Pyrex气泡需要工作约12年后其氦渗透致频率漂移率才会小于1×10-14/天，而ASG气泡中氦渗透致频率漂移率始终小于3×10-17/天，其对铷原子钟频率漂移率的贡献可忽略不计.

在真空环境下，氦渗透的漂移机理与大气环境下的氦渗透一样，属于逆过程.求解方法类似，其对漂移率的影响和气泡内初始气压成正比.同理可计算得真空环境下铷泡内氦气压${{P}_{\text{va}}}(t)$随时间的变化规律为，

${{P}_{\text{va}}}(t)=-\frac{{{P}_{1}}}{a}\sum\limits_{n}{{{{{c}'}}_{n}}}\sin {{\omega }_{n}}a{{\operatorname{e}}^{-\omega _{n}^{2}Dt}}={{P}_{1}}-P(t)$

对(32)式求导后发现，当初始气压为饱和氦气压3.98 mTorr时，二者对铷钟漂移率的贡献完全一样，只是漂移率符号相反而已.

4 结论

本文以圆柱形Pyrex玻璃（康宁7740）气泡和ASG玻璃（康宁1720）气泡为例，从动态边界条件的扩散方程出发，得到大气与真空环境下原子气泡内氦气压随时间变化的数值解.在特定情形下，本文结果可以简化为文献[22]中的稳态近似解，经分析，当气泡厚度较大、玻璃对气体渗透率较小时，使用稳态近似求解会产生较大误差，但就常规厚度（≤2 mm）的Pyrex与ASG玻璃气泡而言，分析频率漂移时的相对误差不超过1%.利用该结果我们评估了两种玻璃材料铷吸收泡中的氦渗透对铷原子钟频率漂移率的影响.结果显示，Pyrex玻璃制成的铷吸收泡在65 ℃环境下工作约12年后，其氦渗透致频率漂移率方可达到<1×10-14/天的水平.而ASG玻璃具有非常小的氦气扩散系数，使用ASG玻璃代替Pyrex玻璃制作铷吸收泡，可显著降低氦渗透对铷原子钟频率漂移率的影响.若使用ASG气泡，在铷原子钟连续工作20年内，氦渗透引起的频率漂移率影响均可<3.0×10-17/天，其对铷原子钟频率漂移率的贡献可忽略不计.本文的数值计算方法也可用于分析其它种类气体在不同玻璃材料的物理渗透过程.但就大气环境里其它气体而言，其分子直径均大于氦气，因此其渗透速率通常慢于氦气[23,24]，又因铷原子钟内氦气和铷原子的碰撞频移系数大于其它种类气体[25]，因此可以忽略大气环境中其它气体渗透对铷原子钟频率漂移的影响.

致谢

我们感谢中国科学院精密测量科学与技术创新研究院的阚辉对基本扩散方程求解的教导与有益讨论，同时也感谢中国科学院精密测量科学与技术创新研究院的明刚对本文手稿的阅读与反馈．

利益冲突

无

参考文献

BUSCA G, FRELECHOZ C, WANG Q, et al.

Space clocks for navigation satellites

[C]// IEEE International Frequency Control Symposium and PDA Exhibition Jointly with 17th European Frequency and Time Forum, Tampa, FL, USA: IEEE, 2003: 172-178.

[本文引用: 1]

VANNICOLA F, BEARD R, WHITE J, et al.

GPS block IIF atomic frequency standard analysis

[C]// Proceedings of the 42nd Annual Precise Time and Time Interval System and Applications Meeting, Reston, USA, 2010: 181-196.

[本文引用: 1]

CUI J Q, MING G, WANG F, et al.

Design and studies of ultra high-performance physics package for vapor-cell rubidium atomic clock

[C]// China Satellite Navigation Conference Proceedings, Beijing, China, 2022: 403-414.

[本文引用: 1]

LIU C, XU F, QU Y, et al.

Analysis on factors influencing frequency drift of rubidium clocks for satellite navigation

[C]// China Satellite Navigation Conference Proceedings, Changsha, China, 2016: 645-652.

[本文引用: 1]

NORTON F J.

Helium diffusion through glass

[J]. J Am Ceram Soc, 1953, 36(3): 90-96.

[本文引用: 1]

WILLIAMS G A, FERGUSON J B.

The diffusion of hydrogen and helium through silica glass and other glasses

[J]. J Am Chem Soc, 1922, 44(10): 2160-2167.

[本文引用: 1]

VANIER J, AUDOIN C. The quantum physics of atomic frequency standards[M]. Boca Raton: CRC Press, 1989: 354-355.

[本文引用: 1]

BLOCH M, MANCINI O, MCCLELLAND T.

Performance of rubidium and quartz clocks in space

[C]// Proceedings of the IEEE International Frequency Control Symposium and PDA Exhibition, New Orleans, USA: IEEE, 2002: 505-509.

[本文引用: 1]

ROGERS W A, BURITZ R S, ALPERT D.

Diffusion coefficient, solubility, and permeability for helium in glass

[J]. J Appl Phys, 1954, 25(7): 868-875.

[本文引用: 8]

ABDULLAH S, AFFOLDERBACH C, GRUET F, et al.

Aging studies on micro-fabricated alkali buffer-gas cells for miniature atomic clocks

[J]. Appl Phys Lett, 2015, 106(16): 163505.

[本文引用: 2]

DELLIS A T, SHAH V, DONLEY E A, et al.

Low helium permeation cells for atomic microsystems technology

[J]. Opt Lett, 2016, 41(12): 2775-2778.

DOI:10.1364/OL.41.002775      PMID:27304286      [本文引用: 2]

Laser spectroscopy of atoms confined in vapor cells can be strongly affected by the presence of background gases. A significant source of vacuum contamination is the permeation of gases such as helium (He) through the walls of the cell. Aluminosilicate glass (ASG) is a material with a helium permeation rate that is many orders of magnitude lower than borosilicate glass, which is commonly used for cell fabrication. We have identified a suitable source of ASG that is fabricated in wafer form and can be anodically bonded to silicon. We have fabricated chip-scale alkali vapor cells using this glass for the windows and we have measured the helium permeation rate using the pressure shift of the hyperfine clock transition. We demonstrate micro fabricated cells with He permeation rates at least three orders of magnitude lower than that of cells made with borosilicate glass at room temperature. Such cells may be useful in compact vapor-cell atomic clocks and as a micro fabricated platform suitable for the generation of cold atom samples.

RUSHTON J A, ALDOUS M, HIMSWORTH M D.

Contributed review: The feasibility of a fully miniaturized magneto-optical trap for portable ultracold quantum technology

[J]. Rev Sci Instrum, 2014, 85(12): 121501.

[本文引用: 12]

ALTEMOSE V O.

Helium diffusion through glass

[J]. J Appl Phys, 1961, 32(7): 1309-1316.

[本文引用: 2]

CHEN K H, WU C M, WU S R, et al.

Influence of atmospheric helium on secondary clocks

[J]. Opt Lett, 2020, 45(14): 4088-4091.

[本文引用: 2]

VON WROBLEWSKI S.

Ueber die natur der absorption der gase durch flussigkeiten unter hohen drucken

[J]. Ann Phys, 1879, 8: 29-52.

[本文引用: 1]

STRAESSLE R, PELLATON M, AFFOLDERBACH C, et al.

Low-temperature indium-bonded alkali vapor cell for chip-scale atomic clocks

[J]. J Appl Phys, 2013, 113(6): 064501.

[本文引用: 1]

PETERS W N, STEIN E K.

Helium permeation compensation techniques for long life gas lasers

[J]. J Phys E: Sci Instrum, 1970, 3(9): 719.

[本文引用: 1]

NORTON F J.

Permeation of gases through solids

[J]. J Appl Phys, 1957, 28(1): 34-39.

[本文引用: 1]

CAMPARO J C, KLIMCAK C M, HERBULOCK S J.

Frequency equilibration in the vapor-cell atomic clock

[J]. IEEE Trans Instrum Meas, 2005, 54(5): 1873-1880.

[本文引用: 1]

HARDING G L.

Helium permeation in all-glass tubular evacuated solar energy collectors

[J]. Sol Energ Mat Sol C, 1981, 5(2): 141-147.

[本文引用: 1]

VAN AMERONGEN G J.

The permeability of different rubbers to gases and its relation to diffusivity and solubility

[J]. J Appl Phys, 1946, 17(11): 972-985.

[本文引用: 2]

CARLÉ C, KESHAVARZI S, MURSA A, et al.

Reduction of helium permeation in microfabricated cells using aluminosilicate glass substrates and Al2O3 coatings

[J]. J Appl Phys, 2023, 133: 214501.

[本文引用: 3]

STANNETT V T, KOROS W J, PAUL D R, et al.

Recent advances in membrane science and technology

[M]// Chemistry. Advances in Polymer Science, 1979, 32: 69-121.

[本文引用: 2]

CAMPARO J C.

Frequency equilibration and the light-shift effect for block IIR GPS rubidium clocks

[C]// Proceedings of the 36th Annual Precise Time and Time Interval Systems and Applications Meeting, Washington, DC, USA, 2004: 393-410.

[本文引用: 1]

HAPPER W.

Optical pumping

[J]. Rev Mod Phys, 1972, 44(2): 149-249.

[本文引用: 2]

/

〈 〉

网站设计版权所有 © 2017 《波谱学杂志》编辑部
地址：湖北省武汉市武昌区小洪山西30号 中科院精密测量科学与技术创新研究院波谱楼 《波谱学杂志》编辑部
邮编：430071　电话/传真：(086)027－87198791   E-mail: magres@wipm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发