引言
目前已有的有效的分割模型包括传统的机器学习模型[6-9]、图割模型[10, 11]和活动轮廓模型[12-17].深度学习也被应用于前列腺区域分割领域[18, 19].Vafaie等[7]利用马尔可夫随机场构建概率评估模型,对前列腺磁共振图像中的像素进行分类,并估计像素所属的区域,但该模型计算量大、分割效果不稳定.目前,在图像分割中被广泛应用的活动轮廓模型可分为两类:基于边缘的模型[12-14]和基于区域的模型[15-17].Li等[12]提出了一种基于边缘的水平集分割模型,该模型加入了距离正则化,解决了水平集演化过程中的周期初始化问题,加快了演化速度,然而当边界较弱时,效果并不理想.Li等[15]利用图像的局部尺度信息构造能量函数,但该模型在分割灰度不均匀的图像时,效果不理想.前列腺的中央腺靠近膀胱处存在一定的弱边界,图像分割时往往会忽略前列腺中央腺的顶部.朱泽华等[14]在基于改进的距离正则化水平集(distance regularization level set evolution,DRLSE)分割模型中,提出了两个指示函数函数,分别分割前列腺强边界和弱边界.Milletari等[19]提出了一种基于体素的全卷积三维分割V-net神经网络模型,虽然在分割结果上取得了一些进展,但在边界较弱的情况下,分割效果较差.
1 理论部分
本文所提的前列腺区域分割模型包括4个步骤:1)读取T2加权磁共振图像;2)采用半径为5个像素的8邻域模板,计算局部二值模式(local binary pattern,LBP)特征图[20];3)利用改进的DRLSE模型对LBP特征图进行粗分割,得到前列腺粗轮廓;4)以粗轮廓为初始状态,采用新的水平集能量函数进行迭代,得到前列腺的精细轮廓.
1.1 粗分割过程
1.1.1 LBP
LBP是由Ojala等[20]首次提出的一种计算局部图像模式的算子,用来描述图像局部纹理特征.基本LBP算法利用邻域模板,以中心像素的灰度值为阈值,将邻域中其他像素的灰度值与中心点进行比较:如果邻域中像素的灰度值大于中心点,则该像素的位置标记为“1”;否则,标记为“0”.在运算结束时,得到一个二进制序列,然后以十进制数为中心点.
但每个相邻点与正方形邻域中心点之间的距离不一致,无法很好地表达中心点与相邻点之间的灰度关系.为了克服这个缺点,本文使用了一个圆形邻域LBP:
其中s为符号函数,R表示圆形邻域的半径,P表示邻域像素的数目,
1.1.2 DRLSE
DRLSE是由Li等[12]在2010年提出的改进的活动轮廓模型,是一种基于边缘信息的水平集分割方法.它通过引入一个新的距离正则化项,在传统活动轮廓模型的能量函数中加入一个内能函数来修正水平集与符号距离函数之间的偏差,从而避免水平集的重新初始化.模型的能量函数如(3)式所示:
其中,
其中,ε表示函数宽度,常取1.5.
1.1.3 对DLRSE的改进
在原始的DRLSE模型中,g函数在进化过程中用于外部约束.对于灰度分布不均匀的图像,边缘指示函数收敛速度慢,在弱边界容易产生误差.因此,本文提出了一种改进的基于图像阈值的边缘指示函数,并讨论了其减小误差的能力.
新的边缘指示函数gnew利用了Otsu[23]提出的自适应阈值原理计算阈值:记录T作为目标区域和背景区域的分割阈值;将目标区域中的像素点与图像的比例设置为
图1
图1
改进后gnew函数与原g函数比较.(a)改进后gnew函数;(b)原g函数
Fig.1
Comparison between the improved gnew-function and original g-function. (a) The improved gnew-function; (b) The original g-function
采用基于gnew函数的改进的DRLSE模型对圆形邻域LBP特征图进行分割,提取了前列腺粗轮廓,如图 2所示,然而,提取的前列腺粗轮廓与真实前列腺轮廓仍有一定差距,有待进一步完善,需要进行细分割.
图2
图2
采用改进的DRLSE模型对圆形邻域LBP特征图进行粗分割.(a)初始轮廓;(b)粗分割结果
Fig.2
The improved DRLSE algorithm used to roughly segment the LBP feature map of circular neighborhood. (a) Initial profile; (b) Rough segmentation result
1.2 细分割过程
1.2.1 局部二值拟合(local binary fitting,LBF)模型
将粗分割的结果作为精分割的初始水平集轮廓,并利用所提出的能量函数对前列腺区域进行分割.在Li等[24]的LBF模型中,引入高斯计算器,利用局部灰度信息构造活动轮廓模型,对灰度分布不均匀的前列腺磁共振图像具有一定的应用价值.其能量函数可用(12)式表示:
其中,
其中
1.2.2 本文所提方法
2000年,Xu等[25]提出了一种活动轮廓算法即符号压力(signed pressure force,SPF)的概念,通过统计区域信息改变函数的符号来驱动曲线演化.传统的SPF函数对对比度明显的图像效果较好,但对边界较弱或模糊的图像效果不理想.Zhang等[26]提出了选择性二值滤波和高斯滤波正则化水平集(selective binary and Gaussian filtering regularized level set,SBGFRLS)模型,利用Chan-Vese(CV)[27]模型提出的能量函数对SPF函数进行了改进,但是,该模型计算的是图像的全局灰度,由于缺少惩罚约束,对T2磁共振图像中前列腺区域的分割效果并不理想.
本文利用LBF提出的局部灰度信息,构造了一个新的SPF函数来解决上述问题,其取值范围为
(15) 式中的
前列腺磁共振图像很复杂.由于器官和组织之间的灰度差很小,梯度不明显,而且进化过程中水平集可能超出目标区域的边界.针对上述问题,本研究将原始水平集的能量函数进行优化,构建了一个新的能量函数来约束曲线的演化,可以写成:
在(16)式中,
其中,ν、α、μ、λ为常数项,均为函数的权重系数。将新的边缘指示函数[(10)式]和新的SPF[(15)式]代入(17)式,div表示散度算子,用梯度下降流最小化的公式可以表示为:
2 实验部分
2.1 实验数据
这项研究使用了203组来自SPIE-AAPM-NCI(国际光学与光子学学会-美国医学物理学家协会-国家癌症研究所)前列腺MR分类挑战赛数据库的T2W序列图像集,每组图像分别来自一位不同的患者.
2.2 参数设置
本实验是在WIN10x64位操作系统,Matlab R2018a下进行的。经过优化,使用的参数为:
2.3 评价指标
本文将医生手工分割结果作为金标准,分别采用95% Hausdorff距离(95% HD)、Dice系数(Dice similarity coefficient)、相对体积差(relative volume difference,RVD)作为指标,对所提模型分割精度进行评价.评价指标均采用文献[28]所提出的公式.
Dice系数用(19)式表示:
在(19)式中,
RVD通过以下公式定义:
其中
HD用于评估两条曲线之间的误差.将医生手工分割及模型分割的前列腺轮廓分别定义为像素集A和像素集B,HD可表示为:
3 结果与讨论
3.1 本文模型与手动分割结果的比较
图 3显示了两个患者的前列腺轮廓,分别使用本文所提模型和手动分割获得.
图3
图3
本文所提分割模型与手工分割结果比较,上、下两行分别代表两个不同的患者.左、中、右三列分别代表前列腺底部、中部和顶部的切片.绿色轮廓是由经验丰富的医生手工分割结果,红色轮廓是本文模型分割结果
Fig.3
Comparison between the segmentation results with the algorithm proposed in this research and those with ground truth. The upper and lower lines represent two different patients respectively. The left, middle, and right columns represent the slices of the bottom, middle, and top of the prostate, respectively. Green contour is ground truth, while red contour is segmented by our algorithm
本文所提出模型的Dice系数平均值±标准差为0.94±0.01,表明该模型具有较高的精度.RVD平均值±标准差为-1.21%±2.44%,说明该模型有过分割的倾向,但是由于绝对值接近于0,说明总体分割误差不大,且鲁棒性较好.95% HD数值平均值±标准差为6.15±0.66 mm,该参数表示的是金标准轮廓与模型分割轮廓的误差.
表1 本文所提模型的前列腺分割精度数据
Table 1
| Dice | RVD | 95% HD | |
| 平均值±标准差 | 0.94±0.01 | -1.21%±2.44% | 6.15±0.66 mm |
| 最大值 | 0.96 | 4.85% | 8.62 mm |
| 最小值 | 0.93 | -5.71% | 5.61 mm |
3.2 本文模型与其他模型分割结果的比较
图4
图4
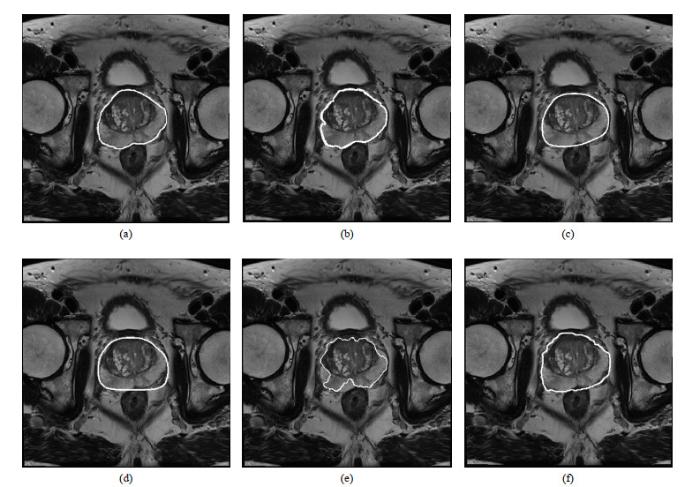
不同模型的前列腺分割结果.(a)金标准;(b)本文所提模型分割结果;(c)文献[19]模型分割结果;(d)文献[15]模型分割结果;(e)文献[12]模型分割结果;(f)文献[7]模型分割结果
Fig.4
The results of prostate segmentation with different algorithms. (a) Ground truth; (b) The proposed algorithm; (c) The algorithm in Ref. [19]; (d) The algorithm in Ref. [15]; (e) The algorithm result in Ref. [12]; (f) The algorithm result in Ref. [7]
基于文献[19]模型的分割结果如图 4(c)所示,表明前列腺周围区存在过分割现象,这可能是由于V-net在训练中使用的损失函数对分割没有较好的限制,导致过分割的产生.在文献[15]的基础上提出的分割模型,在图像灰度分布均匀的情况下,可以得到较好的分割效果.但对于结构复杂、灰度分布不均匀的前列腺图像,分割效果并不理想,如图 4(d)所示,当目标边界较弱,梯度变化不明显时,分割结果中往往存在过分割现象.前列腺图像的梯度信息是用文献[12]中的分割模型计算得到,但是前列腺图像的灰度分布是不均匀的,总是存在弱边界.如图 4(e)所示,模型的边缘指示函数存在许多局部极小值,限制了曲线的演化,导致无法达到目标的真实边界.而本文所提模型通过计算图像的局部信息,较好地分割出前列腺,使曲线更接近真实前列腺边界.文献[7]分割模型,利用概率模型对图像中的区域像素进行建模,并利用概率模型对像素进行分类和评价,判断它们是否属于同一区域.由于前列腺图像存在较大的灰度和结构差异,使用该模型很难获得较好的分割结果,如图 4(f)所示.不同模型的分割精度如图 5所示.
图5
图5
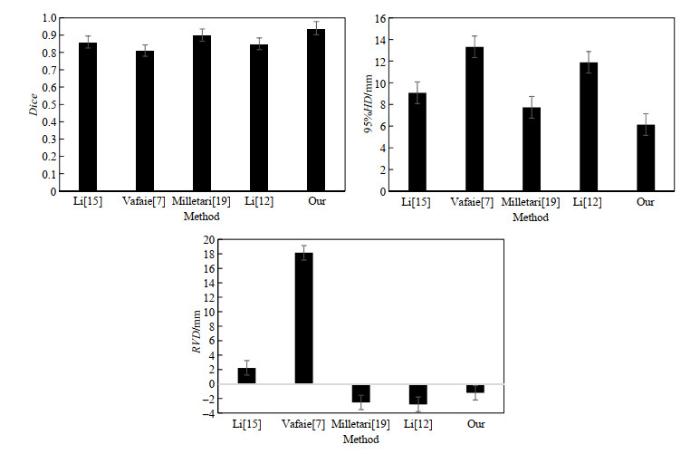
五种模型的前列腺分割精度比较
Fig.5
Comparison of segmentation results of the five algorithms
图 5表明,本文所提模型具有较好的前列腺分割性能.与现有的其他模型相比,该模型与金标准之间的距离差更小、相似度更高,用于前列腺区域分割时,具有较高的精度和鲁棒性.
3.3 讨论
目前,水平集算法是一种常用的医学图像处理方法.参考文献[11]中的分割模型考虑了先验形状信息.在基于形状信息的分割模型中,形状参数需要通过训练数据获得.然而,在真实的前列腺图像中,图像的形状、大小和纹理往往存在较大个体差异,这给应用带来了一定的限制。
本文提出了一种新的前列腺分割模型,可用于分割不同大小和形状的前列腺.在粗分割阶段,采用一种新的边缘指示函数,以图像的阈值为调整因子,改变图像的梯度分布,减小最小梯度,同时保留前列腺的边界,使曲线快速向目标边界演化.本文提出的新分割模型用于粗分割结果的细化.通过计算局部灰度信息,加入了外部能量驱动项和距离正则化项,克服了水平集周期初始化的缺点.利用高斯核函数对图像进行平滑处理,以减少噪声的影响.基于改进了的边缘指示函数,图像梯度分布均匀,较好地保留了前列腺的边缘.实验结果表明,当前列腺与背景区域的对比度较小时,该模型具有较好的性能.使用我们的新模型均可以获得更好的分割结果,是因为该模型结合了前列腺的梯度信息和局部灰度信息进行曲线演化,并将粗分割的结果作为精分割的初始轮廓,避免了零水平集位置对水平集分割的影响.利用该模型得到的分割结果更接近前列腺真实轮廓.
将本文所提模型的分割结果与金标准进行了比较表明,所提模型可以对不同形状的前列腺进行分割,更重要的是,其分割效果明显优于其他分割模型.因此,该模型具有很强的鲁棒性.
4 结论
本文提出了一种基于局部灰度信息和梯度信息的主动轮廓模型来更准确地分割前列腺,对LBF模型中基于局部灰度信息的活动轮廓进行了改进,并提出了一种新的基于局部灰度信息的活动轮廓,引入SPF,并将外部能量项和距离正则化项融合应用于前列腺T2加权磁共振图像序列的分割.首先读取T2加权磁共振图像,然后在构造LBP特征图的同时,利用改进的DRLSE进行粗分割并快速提取粗轮廓.提取的粗分割轮廓作为细分割的初始轮廓,在一定程度上降低了训练消耗的代价.采用基于局部区域和梯度信息的新模型进行精细分割和调整迭代次数,得到了较好的前列腺分割效果.实验结果也表明该模型具有较高的性能.
由于患者的不同,前列腺的外观存在很大的差异,未来的工作将集中在将该模型采用更大的数据集进行测试.
无
参考文献
A deep learning approach for real time prostate segmentation in freehand ultrasound guided biopsy
[J].DOI:10.1016/j.media.2018.05.010 [本文引用: 1]
Segmentation of right ventricle in cardiac cine MRI using COLLATE fusion-based multi-atlas
[J].
基于COLLATE融合多图谱的心脏电影MRI右心室分割
[J].
Application of histogram analysis of dynamic enhanced MRI quantitative parameter in the diagnosis of prostate cancer
[J].DOI:10.3969/j.issn.1672-5131.2020.12.035 [本文引用: 1]
动态增强MRI定量参数直方图分析在诊断前列腺癌中的应用
[J].DOI:10.3969/j.issn.1672-5131.2020.12.035 [本文引用: 1]
Biparametric (bp) and multiparametric (mp) magnetic resonance imaging (MRI) approach to prostate cancer disease: a narrative review of current debate on dynamic contrast enhancement
[J].DOI:10.21037/gs-20-547 [本文引用: 1]
Prostate cancer diagnosis based on cascaded convolutional neural networks
[J].
基于级联卷积神经网络的前列腺磁共振图像分类
[J].
Correlation of magnetic resonance imaging with digital histopathology in prostate
[J].
In vivo MRI based prostate cancer identification with random forests and auto-context model
[J].
The use of atlas registration and graph cuts for prostate segmentation in magnetic resonance images
[J].DOI:10.1118/1.4914379 [本文引用: 1]
Superpixel-based segmentation for 3D prostate MR images
[J].DOI:10.1109/TMI.2015.2496296 [本文引用: 2]
Distance regularized level set evolution and its application to image segmentation
[J].DOI:10.1109/TIP.2010.2069690 [本文引用: 9]
Research on the segmentation method of prostate magnetic resonance image based on level set
[J].
基于水平集的前列腺磁共振图像分割方法研究
[J].
Segmentation of prostate magnetic resonance images based on an improved distance regularized level set evolution (DRLSE) model
[J].
基于改进DRLSE模型的前列腺磁共振图像分割
[J].
Minimization of region-scalable fitting energy for image segmentation
[J].DOI:10.1109/TIP.2008.2002304 [本文引用: 7]
Level set based on signed pressure force function and its application in liver image segmentation
[J].
ZHANG. Active contours driven by local image fitting energy
[J].DOI:10.1016/j.patcog.2009.10.010 [本文引用: 2]
Accurate and robust deep learning-based segmentation of the prostate clinical target volume in ultrasound images
[J].DOI:10.1016/j.media.2019.07.005 [本文引用: 1]
Multiresolution gray-scale and rotation invariant texture classification with local binary patterns
[J].
A variational level setapproach to multiphase motion
[J].DOI:10.1006/jcph.1996.0167 [本文引用: 1]
A threshold selection method from gray-level histogram
[J].DOI:10.1109/TSMC.1979.4310076 [本文引用: 1]
A level set method for image segmentation in the presence of intensity inhomogeneities with application to MRI
[J].DOI:10.1109/TIP.2011.2146190 [本文引用: 2]
Active contours with selective local or global segmentation: A new formulation and level set method
[J].DOI:10.1016/j.imavis.2009.10.009 [本文引用: 1]
Active contours without edges
[J].DOI:10.1109/83.902291 [本文引用: 1]
Evaluation of prostate segmentation algorithms for MRI: The PROMISE12 challenge
[J].DOI:10.1016/j.media.2013.12.002 [本文引用: 2]
Visual saliency-based active learning for prostate magnetic resonance imaging segmentation
[J].