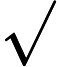关键词: Convex quadratic programming, predictor-corrector, interior-point algorithm

Abstract:

This article presents a polynomial predictor-corrector interior-point algorithm for convex quadratic programming based on a modified predictor-corrector interior-point algorithm. In this algorithm, there is only one corrector step after each predictor step, where Step 2 is a predictor step and Step 4 is a corrector step in the algorithm. In the algorithm, the predictor step decreases the dual gap as much as possible in a wider neighborhood of the central path and the corrector step draws iteration points back to a narrower neighborhood and make a reduction for the dual gap. It is shown that the algorithm has ${\rm O}(\sqrt n L)$ iteration complexity which is the best result for convex quadratic programming so far.

Key words: Convex quadratic programming, predictor-corrector, interior-point algorithm