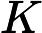数学物理学报(英文版) ›› 2022, Vol. 42 ›› Issue (2): 769-773.doi: 10.1007/s10473-022-0221-x
A NOTE ON MEASURE-THEORETIC EQUICONTINUITY AND RIGIDITY
罗炽逸, 赵云
- School of Mathematical Sciences and Center for Dynamical Systems and Differential Equations, Soochow University, Suzhou 215006, China
A NOTE ON MEASURE-THEORETIC EQUICONTINUITY AND RIGIDITY
Chiyi LUO, Yun ZHAO
- School of Mathematical Sciences and Center for Dynamical Systems and Differential Equations, Soochow University, Suzhou 215006, China
摘要: Given a topological dynamical system and a -invariant measure , let denote the Borel -algebra on . This paper proves that is rigid if and only if is --equicontinuous in the mean for some subsequence of , and a function is rigid if and only if is --equicontinuous in the mean for some subsequence of . In particular, this gives a positive answer to Question 4.11 in [1].}
中图分类号:
- 37A05