网络数据是指用有向图或者无向图作为一种通用语言的数据, 在生活中也很普遍, 例如新冠病毒传播网络、基因网络、金融网络、交通网络、通话网络等. 对于网络数据的分析, 过去的研究主要是集中在对于网络结构的分析上. 对此, 学者们提出了许多模型来描述网络结构, 最初是对空间结构进行描述, 因而对于网络模型的构建是建立在空间模型的基础上. Ord^[19]提出了空间自回归 (SAR) 模型, 它研究了空间结构对于用户所产生的影响. 基于 SAR 模型, Anselin^[1]提出了空间杜宾模型, 该模型考虑了协变量与误差项的相关性, 之后相继提出了空间误差模型与 SAR 组合模型, LeSage 和 Pace^[15]从空间数据出发, 给出了更一般的空间自回归模型, 将上述模型都包含其中.

为了研究网络结构对于用户所带来的影响, 基于 SAR 模型, Chen 等^[5]提出了网络自回归 (NAR) 模型. 随后, Zhu 等^[26]考虑了大规模社交网络中 NAR 模型, 并给出了 NAR 模型的平稳性. 已有的文献大多都假设 NAR 模型中各种节点之间是不存在差别的, 很少对节点的异质性进行考虑. 为了弱化这一假设, Malikov 和 Sun^[18]提出一种灵活的半参数 SAR 模型, 允许空间自回归参数在单元间变化, 从而允许变量识别特定社区的空间依赖性. Zhu 和 Pan^[25]基于 NAR 模型, 建立了分组 NAR 模型, 将网络个体划分不同的组, 不同组的 NAR 模型具有不同的参数; Chen 等^[4]提出了社区 NAR 模型, 基于拥有 $N$ 个节点与 $K$ 个社区的随机块模型生成邻接矩阵, 从而允许跨不同网络社区的异构网络效应存在.

但无论是分组 NAR 还是社区 NAR, 同一个组或者同一个社区中的节点之间只要存在边就会存在影响, 但实际中会存在同一类型的节点之间不存在直接相连的边, 只有不同类型的节点之间才会存在直接相连的边从而产生影响. 双模网络就是针对这种网络的简单情况而提出的, Borgatti 和Everett^[2]、Li 和 Chen^[16]、Cai 和 Liu^[3]等都观察到了双模网络结构, 如买家与卖家间的交易、选民与候选人间的投票、导演与演员间的合作等; 但以往的研究主要集中在分析网络结构上, 如: 基于双模网络 Everett 和Borgatti^[8]以及 D'Esposito^[7]等研究了可视化, Li 和 Chen^[16]以及 Gao 和Chen^[10]研究了链路预测, Feng 等^[9]以及 Cai 和 Liu^[3]研究了社区检测等. 为了突破对双模网络结构的研究, 进一步研究双模网络中响应变量的依赖性, Huang 等^[12]从无向图视角提出了双模 NAR 模型, 首先利用传统网络估计方法--拟极大似然估计 (QMLE) 方法进行参数估计, 但是在 QMLE 计算过程中存在大规模矩阵行列式的计算, 计算量复杂, 进而采用了基于最优线性预测 (BLP) 的最小二乘估计 (LSE) 方法来提升计算效率, 并在不同情况下进行了数值模拟, 发现两种方法的估计性能都较高, 同时 LSE 的计算效率优于 QMLE 的计算效率.

在实际中, 不止存在双模网络数据, 还存在大量的三模网络数据, 即一个网络中存在三种类型的节点, 同类型节点不直接相连, 不同类型的节点之间才可以直接相连, Everett 和 Borgatti^[8]在文中提到过三模数据, 并指出了一个犯罪行为按受害者分类可以构成三模网络数据集. Fan^[20]在文中提到了一个三模数据, 即学生-话题- 知识网络, 包括三种数据类型: 学生、讨论话题、知识术语. 此外还存在其他三模数据, 如: 第三方平台中商家、顾客、配送员所构成的网络, 校园评价系统中学生、老师、家长所构成的网络等. 因此, 本文基于 Huang 等^[12]所提出的双模 NAR 模型进行拓展, 考虑了三模 NAR 模型.

本文在第 2 节给出了三模网络的定义以及其向量表达形式, 并给出模型的可逆性以及参数可识别性条件, 进而研究了 QMLE 和基于 BLP 的 LSE 两种估计方法以及估计量的大样本性质. 第 3 节主要进行了数值模拟, 首先介绍了三模网络数据的生成方法, 同时考虑了参数、权重矩阵、误差分布的不同设置, 进而考虑了两种估计方法并计算效率, 同时与双模 NAR 模型的结论进行了对比, 第 4 节中利用模型对不同年龄段的电影评分网络际数据进行了拟合. 第 5 节对本文进行了总结, 并进行了展望.

三模网络是指在一个无向网络结构中, 存在三种类型不同的节点, 同种类型的节点之间不存在边, 只有不同类型的节点之间才有边相连从而产生联系, 且不存在自环与多重边. 三模网络的例子很多, 例如, 在第三方外卖平台上, 存在三种类型的节点, 类型 I 的节点表示顾客, 类型 II 的节点表示商家, 类型 III 的节点表示配送员. 一条边存在表示如果三者之间任意两者进行了评论或反馈, 在第三方平台上无论顾客之间、商家之间、配送员之间、个人本身是不能够进行评价的, 因而同种类型的节点是不直接相连的. 因此, 该网络可以看作是一个三模网络. 下面, 我们对三模网络结构进行一些限制与定义:

假设在一个三模网络中, 共有 $N$ 个节点, 其中类型 I 的节点有 $n_1$ 个, 类型 II 的节点有 $n_2$ 个, 类型 III 的节点有 $n_3$ 个, 记$N=n_1+n_2+n_3$. 为了计算简单, 我们假定:${\lim\limits_{n_1\rightarrow+\infty \atop n_2\rightarrow+\infty }\frac{n_1}{n_2}=c_1},{\lim\limits_{n_1\rightarrow+\infty \atop n_3\rightarrow+\infty }\frac{n_1}{n_3}=c_2},$其中, $c_1$ 与 $c_2$ 均为有限常数, 这个假定之后可以进一步减弱为: 当 $n_1$、$n_2$、$n_3$ 分别趋于无穷时, 它们是同阶的.进而定义三种类型节点之间的邻接矩阵:$A_{kl}=(a_{i_ki_l})\in \mathbb{R}^{n_k\times n_l},$其中, ${1\leqslant i_k \leqslant n_k}$, ${1\leqslant i_l \leqslant n_l}$, ${1\leqslant k\ne l \leqslant 3}$. 若$(a_{i_ki_l})=1$, 则表示 $i_k$ 到 $i_l$ 之间存在一条边; 若 $(a_{i_ki_l})=0$, 则表示 $i_k$ 到 $i_l$ 之间不存在边, 进而可以得到该网络的邻接矩阵为:$A=[\textbf{0}_{n_1\times n_1},A_{12},A_{13}; A_{21},\textbf{0}_{n_2\times n_2},A_{23};A_{31},A_{32},\textbf{0}_{n_3\times n_3}]\in \mathbb{R}^{N\times N}.$

为了更好地刻画网络中各个节点的相邻程度, 构建权重矩阵. 定义 $W_{kl}=(w_{kl,i_ki_l})=(a_{i_ki_l}/d_{i_k})$, 其中, $d_{i_k}=\sum\limits_{m=1}^{N} a_{i_km}$ 是 $k$ 类型的节点相对于其他类型节点的出度. 同时, 也可采取其他方式来定义权重矩阵, 例如, 利用矩阵的最大特征值来分割所有元素来定义权重矩阵, Kelejian 和 Prucha^[13]对权重矩阵进行了更加详细的描述与证明. 我们之后的模拟结果也说明了针对权重矩阵的不同生成方式, 模拟表现较好. 首先采用行标准化的方式对邻接矩阵进行标准化, 得到$W=[\textbf{0}_{n_1\times n_1},W_{12},W_{13}; W_{21},\textbf{0}_{n_2\times n_2},W_{23};W_{31},W_{32},\textbf{0}_{n_3\times n_3}]\in \mathbb{R}^{N\times N}.$

每一个类型的节点 $i_1$(${1\leqslant i_1 \leqslant n_1}$), $i_2$(${1\leqslant i_2 \leqslant n_2}$) 或 $i_3$(${1\leqslant i_3 \leqslant n_3}$) 分别对应一个响应变量 $Y_{1,i_1}, Y_{2,i_2}$ 或$Y_{3,i_3}$, 定义 $Y_1=(Y_{1,1},\cdots,Y_{1,n_1})^T, Y_2=(Y_{2,1},\cdots,Y_{2,n_2})^T$, $Y_3=(Y_{3,1},\cdots,Y_{3,n_3})^T$. 为了增强响应变量的解释能力, 我们借助 LeSage 和 Pace^[15]中对于不同类型的响应节点引入不同的外生协变量, 分别将类型 I、II 和 III 节点的外生变量定义如下: $X_1=(X_{1,1}^T, \cdots,X_{1,n_1}^T)^T\in \mathbb{R}^{n_1\times p_1}$, $X_2=(X_{2,1}^T,\cdots,X_{2,n_2}^T)^T\in \mathbb{R}^{n_2\times p_2}$, $X_3=(X_{3,1}^T,\cdots,X_{3,n_3}^T)^T\in \mathbb{R}^{n_3\times p_3}$, 其中 $X_{i,j}$ 为节点$Y_{i,j}$ 对应的外生变量值, 维数为 $p_i$ 维. 基于文献[14,24], 我们假定 $X_1$, $X_2$ 和$X_3$ 都是常数回归量, 进而可以构造三模 NAR 模型, 形式如下

其中假定 $\varepsilon_1$, $\varepsilon_2$ 和 $\varepsilon_3$ 是相互独立的, 并且 ${\rm Cov}(\varepsilon_1)=\sigma_1^{2}{\bf I}_{n_1}$, ${\rm Cov}(\varepsilon_2)=\sigma_2^{2}{\bf I}_{n_2}$, ${\rm Cov}(\varepsilon_3)=\sigma_3^{2}{\bf I}_{n_3}$, 这里 $\textbf{I}_n\in \mathbb{R}^{n\times n}(n=n_1,n_2,n_3)$ 是单位矩阵. 在上述模型中, $\rho_{kl}({1\leqslant k\ne l \leqslant 3})$ 均为交叉影响效应, 具体地说, $\rho_{12}$ 表示类型 II 的节点对类型 I 节点的影响, $\rho_{13}$ 表示类型 III 的节点对类型 I 节点的影响, $\rho_{21}$、$\rho_{23}$、$\rho_{31}$、$\rho_{31}$ 均可采用相同的方式进行解释. 基于 Liu^[17]和 Cohen-Cole 等^[6], $\beta_1$、$\beta_2$、$\beta_3$ 分别为外生协变量的系数, 表示不同类型节点中外生变量对于自身的影响.

观察式(2.1), 发现模型的参数是较多的, 容易产生过度参数化的问题. 因此为了更好地识别模型参数空间, 将三模 NAR 模型写成向量的形式. 定义以下变量

其中 $p=p_1+p_2+p_3$, 进而三模 NAR 模型可以表示成如下向量形式

因此得到: $Y=(\textbf{I}_{N}-\textbf{W}_{\rho})^{-1}(\textbf{X}\beta+\varepsilon)$, 而 $\textbf{I}_{N}-\textbf{W}_{\rho}$ 的可逆性是求解 $Y$ 的充分条件.

引理 2.1 假定 $|\rho_{12}|+|\rho_{13}|< 1$, $|\rho_{21}|+|\rho_{23}|<1$, $|\rho_{31}|+|\rho_{32}|< 1$, 那么$\textbf{I}_{N}-\textbf{W}_{\rho}$ 是可逆的.

证 根据 Seber^[21], 为了确保 $\textbf{I}_{N}-\textbf{W}_{\rho}$ 的可逆性, 一个充分条件是$|\lambda_{1}(\textbf{W}_{\rho})|<1$, 其中 $\lambda_{j}(W)$ 表示矩阵 $W \in \mathbb{R}^{N \times N}$ 的第 $j$ 个特征值, 且满足$|\lambda_{1}(W)| \geq |\lambda_{2}(W)| \geq \cdots \geq |\lambda_{N}(W)|$. 根据 Gerschgorin 圆盘定理, 若 $\textbf{W}_{\rho}$ 的$\lambda_{1}(W)$的模小于 1, 只需要任一特征值的模小于 1:

其中, $0 \leqslant n_1'\leqslant n_1$, $0 \leqslant n_2'\leqslant n_2$, $0 \leqslant n_3'\leqslant n_3$, $n_1',n_2',n_3'$ 分别表示权重矩阵中的某一行中三种类型节点的非零个数, 那么, 可逆条件可以得到如下结果:$|\lambda_1| \leqslant|\rho_{12}|+|\rho_{13}|< 1,|\lambda_2| \leqslant|\rho_{21}|+|\rho_{23}|< 1,|\lambda_3| \leqslant|\rho_{31}|+|\rho_{32}|< 1.$

在上述条件下, $\textbf{I}_{N}-\textbf{W}_{\rho}$ 是可逆的. 后文中假定引理 2.1 的条件满足, 误差项的协方差矩阵为:$\Sigma_e=[\sigma_1^2\textbf{I}_{n_1},\textbf{0}_{n_1\times n_2},\textbf{0}_{n_1\times n_3};\textbf{0}_{n_2\times n_1},\sigma_2^2\textbf{I}_{n_2},\textbf{0}_{n_2\times n_3};\textbf{0}_{n_3\times n_1},\textbf{0}_{n_3\times n_2},\sigma_3^2\textbf{I}_{n_3}].$因此, 得到 $Y$ 的协方差矩阵为 $\Sigma=(\textbf{I}_{N}-\textbf{W}_{\rho})^{-1}\Sigma_e(\textbf{I}_{N}-\textbf{W}_{\rho}^T)^{-1}$. 对于三模 NAR 模型(2.1), 基于参数的值, 将上述参数空间分为以下 7 种情况: 6 向关系、$\cdots$、单向关系和无跨模式关系, 我们仅以 4 向关系为例进行说明.

假定所有交叉影响效应中仅有 2 个为 0, 其余非 0. 例如, 先假定 $\rho_{12}= 0$, $\rho_{13}=0$, $\rho_{21}\ne0$, $\rho_{23}\ne0$, $\rho_{31}\ne0$ 和$\rho_{32}\ne0$, 在这种情况下说明类型 II 和类型 III 节点之间互相影响, 且都会受到类型 I 节点的影响, 同时类型 II 与类型 III 节点均不对类型 I 节点产生影响, 类型 I 节点主要受到外生变量的影响, 此时类型 I 的节点对于类型 II、III 节点的影响可以转换为对外生变量的影响, 此时的模型可以看作是一种双模 NAR, 而对双模 NAR 的估计需要联合估计否则也会产生内生性问题; 或者假定$\rho_{12}\ne 0$, $\rho_{13}=0$, $\rho_{21}=0$, $\rho_{23}\ne0$, $\rho_{31}\ne0$ 和 $\rho_{32}\ne0$, 在这种情况下说明了类型 II 和类型 III 节点之间的关系是双向的, 而类型 I 与类型 III、 类型 I 与类型 II 节点之间的关系是单向的, 如果将(2.1) 模型分开估计, 会得到一个关于 $\rho_{13}$ 和 $\rho_{21}$ 的有偏估计量, 这是由于 $W_{13}Y_{3}$ 和 $\varepsilon_1$ 之间、$W_{21}Y_{1}$ 和$\varepsilon_2$ 之间存在相关性. 因此, 在 4 向关系中必须采取(2.2)式的形式进行联合估计.

总之, 三模 NAR 模型可以很好地识别在三模网络中各个节点之间的关系, 并将关系分为了 7 种类别.

定义 $S=\textbf{I}_{N}-\textbf{W}_{\rho}$ 和$\theta=(\rho_{12},\rho_{13},\rho_{21},\rho_{23},\rho_{31},\rho_{32},\beta^T,\sigma_1^2,\sigma_2^2,\sigma_3^2)^T\in \mathbb{R}^{p+9 }$. 参考 Huang 等^[12], 拟极大似然函数写为

那么, $\hat{\theta}_M=\arg\max_{\theta}l(\theta)$ 是参数的 QMLE. 在对三模 NAR 模型进行参数估计时, 需要求解得到 $l(\theta)$ 的最大值, 一般可以采用牛顿法进行, 但是由于参数的个数较多, 易出现 Hessian 非正定而使得牛顿法失效, 同时利用二阶导数进行最优化处理过于复杂, 本文采用了拟牛顿法中的 BFGS 算法对拟极大似然函数进行求解.

为了利用 BFGS 算法进行求解, 需要建立对于 $l(\theta)$ 的一阶导数, 计算得到以下指标:$S^{-1}=(\mathbb{A}_{ij}),$各个分量见附录 1.

利用 $\frac{\partial |\textbf{A}|}{\partial t}=|\textbf{A}|\rm{tr}(\textbf{A}^{-1}\frac{\partial \textbf{A}}{\partial t})$ 可以得到 $|S|$ 对于参数 $\rho_{j_1j_2}$ 的导数, 其中 $1 \leq j_1\neq j_2 \leq 3$, ${\rm tr}$ 表示矩阵的迹, 进而得到极大似然函数的一阶导数形式

为了建立 QMLE 估计的相合性与渐近正态性, 根据 Huang 等^[12]针对双模 NAR 模型计算得到的拟极大似然函数的一阶导数与二阶导数形式, 整理得到了三模 NAR 模型的拟极大似然函数的一阶导数与二阶导数形式, 结果如下

其中, $1 \leq j_1\neq j_2 \leq 3$, $1 \leq k_1\neq k_2 \leq 3$, $C_{\sigma_k}=-2^{-1}n_k\sigma_k^{-2}$, $C_{j_1j_2}^{\rho}=-{\rm tr}(\mathbb{W}_{j_1}{j_2}S^{-1})$, $\widetilde{\varepsilon}=\Omega_e^{\frac{1}{2}}\varepsilon$.部分符号的表达式见附录 1.

基于大规模网络自回归模型的假设, 为建立 QMLE 的渐近正态性, 需满足

(1) 网络结构

(1.1) 连通性: 将包含类型 I、II 和 III 三种类型节点的 $N$ 个节点定义为马尔可夫链的状态空间, 假设该马尔可夫链是非周期不可约的, 其转移概率矩阵由权重矩阵 $W$ 确定, 假设平稳分布 $\pi=(\pi_i)^T\in \mathbb{R}^N, \pi_i \ge 0, \Sigma_{i}\pi_i=1 $, 且$\textbf{W}^T\pi=\pi$. 进一步假设下列条件存在: $\Sigma_{i}^N\pi_i^2=O(N^{-\frac{1}{2}-\delta}), 0 < \delta \leq \frac{1}{2}$.

(1.2) 均匀性: 定义对称矩阵 $\textbf{W*}=\textbf{W}+\textbf{W}^T$, 假设 $\textbf{W*}$ 的最大特征值满足$|\lambda_1(\textbf{W*})|$$=O(\log N)$.

(2) 噪声项: 定义 $\widetilde{\varepsilon}=\Omega_e^{\frac{1}{2}}\varepsilon=(\widetilde{\varepsilon}_1, \widetilde{\varepsilon}_2,\cdots, \widetilde{\varepsilon}_N)^T \in \mathbb{R}^N$, 其中 $\Omega_e=\Sigma_e^{-1}$. 假设 $E(\widetilde{\varepsilon_i}^3)=\kappa_3, E(\widetilde{\varepsilon_i}^4)=\kappa_4, c_{\varepsilon_0}=E(\widetilde{\varepsilon_i}^2-1)^4, 1 \leq i \leq N$,$\kappa_3,\kappa_4,c_{\varepsilon_0}$ 均为有限常数.

(3) 协变量: 对于任何一个向量 $x \in \mathbb{R}^p$, $||x||=1$, 假定: $\lim\limits_{N \to +\infty}\frac{||\textbf{X}x||^2}{N}=O(1)$, 其中 $\textbf{X}$ 在 2.1 节给出, 对于向量 $x$ 而言, 定义$||x||=(|x_1|^2+|x_2|^2+\cdots +|x_p|^2)^{1/2}$.

(4) 弱大数定律: 假定在三模网络中, 当 $N \to \infty$ 时有以下极限存在, 且满足

定理 2.1 假设上述条件 (1)-(4) 均满足, 同时假设参数是可识别的, 那么可得到 QMLE 的渐近正态性, 当 $N \to \infty$ 时有: $\sqrt{N}(\hat{\theta}_M-\theta) \overset{\text{d}}{\to} N(\textbf{0}_{p+9},(\Sigma_{2}^M)^{-1}\Sigma_{1}^{M}(\Sigma_{2}^M)^{-1}),$ 其中 $\overset{\text{d}}{\to}$ 表示依分布收敛, 同时假定 $\Sigma_{1}^{M}$ 和 $\Sigma_{2}^{M}$ 均为正定矩阵, 其表达式见附录2.

定理 2.1 的证明借鉴了 Huang 等^[12]在双模 NAR 模型 QMLE 渐近正态性证明中得到的结论:$\sqrt{N}(\hat{\theta}_M-\theta)=\{-\frac{\ddot{l}(\theta^*)}{N}\}^{-1}\{\frac{\dot{l}(\theta)}{\sqrt{N}}\}$,其中 $\theta^*$ 在 $\theta$ 与 $\hat{\theta}_M$ 之间, 同时有下式成立:

其中, $\overset{p}{\to}$ 表示依概率收敛.

Huang 等^[12]指出了对于计算 $|\textbf{I}_N-W_{\rho}|$ 会有很大的计算量从而产生很大的代价, 计算复杂度高达 $O(N^3)$, 进而与 LSE 方法进行了比较, 指出了 LSE 计算效率优于 QMLE, 在三模 NAR 模型中, $|\textbf{I}_N-W_{\rho}|$ 虽然也存在很大的计算量, 但对于与 LSE 计算效率的比较还需要进一步验证.

采用拟极大似然法进行参数估计的时候, 需要计算 $\textbf{I}_{N}-\textbf{W}_{\rho}$ 的行列式值, 当网络规模 $N$ 很大时, 计算量会很大. 为了解决这一问题, 基于 Shumway 和 Stoffer^[22]所提出的 BLP, Huang^[11]提出了一种基于 BLP 的最小二乘估计方法. 定义 $\tilde{Y}_i=Y_i-\mu_i$ 和 $\tilde{Y}_{(-i)}=Y_{(-i)}-\mu_{(-i)}$, 其中 $\mu_i=E(Y_i)$, $Y_{(-i)}=\{Y_j:j\ne i,1 \leqslant j \leqslant N\}$ 和 $\mu_{(-i)}=E(Y_{(-i)})$. 在给定$\tilde{Y}_{(-i)}$ 的条件下, 考虑 $\tilde{Y}_i$ 的 BLP. 用 $\mathcal{N}_1$, $\mathcal{N}_2$, $\mathcal{N}_3$ 分别表示类型 I、 II、 III 的节点集合, 那么, 可以得到如下引理:

引理 2.2 如果 $j_1,j_2,j_3 \in \{1,2,3\},i\in N_j,j_1 \neq j_2 \neq j_3$, 那么在给定 $\tilde{Y}_{(-i)}$ 的条件下, $\tilde{Y}_i$ 的 BLP 存在.

该引理的证明见附录 3. 考虑基于 $\tilde{Y}_i$ 的 BLP 来构造目标函数. 最小二乘估计方法需要两步才可以得到误差项方差的估计, 但为了简便, 这里并未考虑误差项方差的估计, 因而两种估计方法的感兴趣的参数的维度不同. 定义:$\gamma=(\rho_{12},\rho_{13},\rho_{21},\rho_{23},\rho_{31},\rho_{32},\beta^T)^T\in \mathbb{R}^{p+6},$目标函数则可以写为

定义 $\Omega=S^T\Sigma_{e}^{-1}S$, $m=\{{\rm diag}(\Omega)\}^{-1}$ 和$Y_c=\{\mathcal{F}\{\tilde{Y}_{(i)}|\tilde{Y}_{(-i)}\},i=1,2,\cdots,N\}$, 其中 ${\rm diag}(A)$ 表示矩阵 $A$ 的对角矩阵, 进而可以将目标函数写为向量形式, 通过文献[12]得到的结论, 可以得到:$Y_c=-m(\Omega-m^{-1})(Y-u),$其中 $u=E(Y)=S^{-1}\textbf{X}\beta$. 因此, 最小二乘目标函数可以构造为

其中 $\tilde{Y}=\{Y_i-\mu_i,1\leqslant i \leqslant N\}$, 且 Huang 等^[12]已经给出了基于双模 NAR 形式的(2.4)和(2.5)式的证明, 在三模 NAR 模型中, 形式并未发生改变, 证明思路类似, 此处省略细节. 那么, $\hat{\gamma}_M=\arg\min_{\gamma}Q(\gamma)\in \mathbb{R}^{p+ 6 }$. Huang^[11]所提出的基于 BLP 的最小二乘估计, 在计算的过程中并未涉及到对于大规模矩阵的行列式计算, 其次, 虽然涉及到了矩阵的逆, 即 $m$ 和 $\Sigma_e$ 的逆, 但是 $m$ 和 $\Sigma_e$ 均为对角矩阵, 逆的求解可以直接通过对角线元素求逆的方式得到, 同时, $Q(\gamma)$ 中只涉及到了节点之间直接相连或间接相连的关系. 综合考虑, 该方法在大规模网络自回归模型中是可行的, 仅仅有一点要求即需要保证该大规模网络尽可能稀疏, 即该网络中边的数量尽可能少. 为了估计参数, 同样采用拟牛顿法的 BFGS 算法对 $Q(\gamma)$ 函数进行求解.

为了利用 BFGS 算法进行求解, 需要建立对于 $Q(\gamma)$ 的一阶导数. 为了方便计算, 先对 $Q(\gamma)$ 的形式进行适当调整变形

其中, $F=mS^T\Sigma_e(SY-\textbf{X}\beta)$, 在此基础上为了计算 $Q(\gamma)$ 的一阶导数, 先建立以下指标

其中

因而通过计算可以得到 $Q(\gamma)$ 的一阶导数形式, 具体表达式见附录 4.

根据 Huang 等^[12]针对双模 NAR 模型整理的 $Q(\gamma)$ 的一阶与二阶导数形式, 整理得到三模 NAR 模型的最小二乘估计的导数形式, 首先定义如下指标:$\widetilde{S}=\Sigma_e^{-1}S=\Omega_eS$, $ M_1=m\widetilde{S}^T\Sigma_e^{1/2}$, $M_{2,j_1j_2}=(\frac{\partial m}{\partial \rho_{j_1j_2}}\widetilde{S}^T+m\frac{\partial \widetilde{S}^T}{\partial \rho_{j_1j_2}}+m\widetilde{S}^T\frac{\partial S}{\partial \rho_{j_1j_2}}S^{-1})\Sigma_e^{1/2}$, $M_{3,j_1j_2}=m\widetilde{S}^T\frac{\partial S}{\partial \rho_{j_1j_2}}S^{-1}$, $ J_{1,j_1j_2}=M_{3,j_1j_2}\textbf{X}\beta$, $M_{j_1j_2}=M_1^TM_{2,j_1j_2}, J_{j_1j_2}=M_1^TJ_{1,j_1j_2}$, $ H=-2(m\widetilde{S}^T\textbf{X})^TM_1$.从而可以得到最小二乘估计函数的一阶导数与二阶导数形式

为了建立 LSE 估计的渐近正态性, 首先需要参数的可识别性. 利用 Yang 和 Lee^[24]SAR 模型参数可识别性的方法计算最小二乘目标函数的期望, 从而建立参数的可识别性.

首先, 定义一些参数真值: $\gamma_0=(\rho_{0,12},\rho_{0,13},\rho_{0,21},\rho_{0,23},\rho_{0,31},\rho_{0,32},\beta_0^T)^T$ 为真实的网络交叉效应系数与外生协变量系数, 真实的误差项方差分别为 $\sigma_1^2,\sigma_2^2,\sigma_3^2$. 那么, 真实的误差项协方差矩阵可以用$\Sigma_{e0}$ 来表示. 进一步定义:$S_0=\textbf{I}_N-W_{\rho_0},\Sigma_0=S_0^{-1}\Sigma_{\rho_0}(S_0^T)^{-1},$其中, $W_{\rho_0}$ 通过将(2.2)式中 $W_{\rho}$ 的参数替换为相应真值得到.

定义 $\mathbb{Q}(\gamma)=E(Q(\gamma))$, 根据 Huang 等^[12]得到的关于 $Q(\gamma)$ 期望的计算结果,$\mathbb{Q}(\gamma)=||mS^T(\Sigma_e^{-1}\otimes\textbf{I})(SS_0^{-1}(\textbf{I}_p\otimes\textbf{X})\beta_0-(\textbf{I}_p\otimes\textbf{X})\beta||^2+{\rm tr}(m\Omega\Sigma_0\Omega m),$其中, $\otimes$ 为 Kronecker 积, 将上式应用于三模 NAR 模型, 得到$\mathbb{Q}(\gamma)=||m\widetilde{S}^T(SS_0^{-1}\textbf{X}\beta_0-\textbf{X}\beta||^2+{\rm tr}(m\Omega\Sigma_0\Omega m).$

根据 White^[23]的结论, 上式表明:$\liminf\limits_{n \to \infty}\min\limits_{\theta \in \bar{B}_{\epsilon}(\theta_0)}\frac{\mathbb{Q}(\gamma)-\mathbb{Q}(\gamma_0)}{N} > 0,$其中, $\bar{B}_{\epsilon}(\theta_0)$ 是 $\theta_0$ 的直径为 $\epsilon$ 的开邻域的补集, 进而根据 NAR 模型中常用的参数可识别性的方法建立以下假设:

(5) 参数可识别条件: 假定在三模网络中 $\lim\limits_{N \to +\infty}N^{-1}(\widetilde{\mathbb{X}}^T\widetilde{\mathbb{X}})$ 存在并且非奇异, 其中:

$\mathbb{X}_1=\mathbb{W}_{12}S_0^{-1}\textbf{X}\beta_0,\mathbb{X}_2=\mathbb{W}_{13}S_0^{-1}\textbf{X}\beta_0,\mathbb{X}_3=\mathbb{W}_{21}S_0^{-1}\textbf{X}\beta_0,\mathbb{X}_4=\mathbb{W}_{23}S_0^{-1}\textbf{X}\beta_0,\mathbb{X}_5=\mathbb{W}_{31}S_0^{-1}\textbf{X}\beta_0,$

$\mathbb{X}_6=\mathbb{W}_{32}S_0^{-1}\textbf{X}\beta_0,\mathbb{X}=(\mathbb{X}_1,\mathbb{X}_2,\mathbb{X}_3,\mathbb{X}_4,\mathbb{X}_5,\mathbb{X}_6) \in \mathbb{R}^{N \times 6},\widetilde{\mathbb{X}}=(\mathbb{X},\textbf{X}) \in \mathbb{R}^{N \times (6+p)}.$

该假设与 NAR 中常用参数可识别性假设基本一致, 在此不进行证明. 但是观察该假设发现: $\widetilde{\mathbb{X}}$ 中含有系数 $\beta$, 若自回归模型中不存在外生协变量项, 即外生协变量系数为 0, 那么该假设并不能保证参数的可识别性, 因为该假设仅为一个充分性假设. 因此, 建立关于交叉影响效应与外生协变量系数的可识别性.

引理 2.3 如果条件 (5) 满足, 那么存在 $\delta > 0$, 使得

其中, $\lambda_{\min}(*)$ 表示最小特征值, $c$ 是一个常数.

如果参数可识别条件满足, 引理 2.3 表明在参数空间 $\{(\rho_{12},\rho_{13},\rho_{21},\rho_{23},\rho_{31},\rho_{32}):\max\{ |\rho_{12}|$$+|\rho_{13}|,|\rho_{21}|+|\rho_{23}|,|\rho_{31}|+|\rho_{32}|\} \le 1-\delta\}$ 中交叉影响效应与外生协变量系数是可识别的. 同时, 即使三模 NAR 模型中不存在外生协变量, 那么只需要假定 $\textbf{I}$、$W$、$W^T$、$W^TW$ 是线性独立的, 那么对于 LSE 而言, 交叉效应系数也是可以识别的.

(6) 弱大数定律: 假定在三模网络中, 当 $N \to \infty$ 时有以下极限存在, 且满足

其中, $\textbf{1}_N$ 是一个元素为 1 的 $N$ 维列向量.

定理 2.2 假设上述条件 (1)-(3)、(5)-(6) 均满足, 那么可以得到 LSE 估计参数的渐近正态性, 当 $N \to \infty$ 时有: $\sqrt{N}(\hat{\gamma}_L-\gamma) \overset{d}{\to} N(\textbf{0}_{p+6},(\Sigma_{2}^L)^{-1}\Sigma_{1}^{L}(\Sigma_{2}^L)^{-1}),$其中 $\Sigma_1^L$ 和 $\Sigma_2^L$ 的表达式见附录 5.

定理 2.2 的证明借鉴了 Huang 等^[12]在双模 NAR 模型中 LSE 方法渐近正态性证明中得到的结论:$\sqrt{N}(\hat{\gamma}-\gamma)=\{-\frac{\ddot{Q}(\gamma)}{N}\}^{-1}\{\frac{\dot{Q}(\gamma)}{\sqrt{N}}\}$,其中 $\theta^*$ 在 $\theta$ 与 $\hat{\theta}_M$ 之间, 同时有下式成立

本文模拟所使用的电脑的处理器为 12th Gen Intel(R) Core(TM) i7-12700H 2.30 GHz, 该处理器是基于 x64 的 64 位操作系统.

为了说明三模 NAR 模型在有限样本下的表现, 利用 MATLAB 从多方面进行模型的估计与验证. 在每一次模拟中, 首先需要生成邻接矩阵 $A$, 对于一个固定大小的网络规模 $N$, 令:$n_1=\frac{5}{12}N,n_2=\frac{4}{12}N,n_3=\frac{3}{12}N.$在三模网络中, 容易发现三模网络中参数较多, 各个节点之间也存在着联系, 从而容易产生参数的内生性与相依性问题. 为了降低内生性与相依性对于参数估计的影响, 我们在后续生成该网络的过程中保证网络尽可能地稀疏, 即该网络中实际存在的边的数量尽可能地少. 因此, 针对邻接矩阵$A_{21}\in \mathbb{R}^{n_2\times n_1}$ 而言, 采用下述两个步骤进行生成.

步骤 1 生成 $n_2$ 个独立同分布的随机变量, 均服从均值为 4 的指数分布. 用 $E_i(1 \leqslant i\leqslant n_2)$ 表示这些随机变量, 用 $[E_i]$ 表示这些随机变量的整数部分.

步骤 2 对于类型 II 的每一个节点 $i(1 \leqslant i\leqslant n_2)$, 选择 $d_i=\min([E_i],n_1)$ 个节点作为与它相连的类型 I 节点的数目, 进而从类型 I 的节点中随机选择 $d_i$ 个节点作为与类型 II 节点相连的类型 I 节点数目.

通过上述步骤可以得到 $A_{21}$, 采用同样的生成步骤, 可以得到 $A_{31}$, $A_{32}$, 并根据 $A_{12}=A_{21}^T$, $A_{13}=A_{31}^T$, $A_{23}=A_{32}^T$ 可以得到 $A_{12}$、$A_{13}$ 和 $A_{23}$, 并得到邻接矩阵 $A=(a_{ij})\in \mathbb{R}^{N\times N}$. 为了简化计算过程同时减少参数, 假定三种类型的节点拥有相同的外生变量, 即 $p_1=p_2=p_3=1$, $p=3$, 且外生变量 $\textbf{X}$ 是由一个均值为$\textbf{0}_N$, 协方差阵为 $\textbf{I}_N$ 的多元正态分布生成. 最后, 在模拟的过程中, 考虑了权重矩阵、交叉效应、噪声分布的不同设置.

邻接矩阵 给定邻接矩阵 $A$, 我们考虑上文两种标准化方式来获得权重矩阵 $W$. 在行标准化的情形下, 我们定义$W_{12}$、$W_{13}$、$W_{21}$、$W_{23}$、$W_{31}$、$W_{32}$ 通过对 $A$ 的每一行除以行和的方式进行标准化获得. 在特征值标准化的情形下, 我们根据文献[13]中的方法, 通过 $A$ 的最大特征值来分离所有元素从而标准化 $A$ 来获得权重矩阵 $W$.

交叉效应 我们考虑上一节所提出的 7 种情况

情况 1 $\rho_{12}=\rho_{21}=\rho_{31}=\rho_{32}=0.3$, $\rho_{13}=\rho_{23}=0.2$;

情况 2 $\rho_{12}=\rho_{21}=\rho_{31}=\rho_{32}=0.3$, $\rho_{13}=0$, $\rho_{23}=0.2$;

情况 3 $\rho_{21}=\rho_{31}=\rho_{32}=0.3$, $\rho_{12}=\rho_{13}=0$, $\rho_{23}=0.2$;

情况 4 $\rho_{31}=\rho_{32}=0.3$, $\rho_{12}=\rho_{13}=\rho_{21}=0$, $\rho_{23}=0.2$;

情况 5 $\rho_{31}=0.3$, $\rho_{12}=\rho_{13}=\rho_{21}=\rho_{32}=0$, $\rho_{23}=0.2$;

情况 6 $\rho_{12}=\rho_{13}=\rho_{21}=\rho_{31}=\rho_{32}=0$, $\rho_{23}=0.2$;

情况 7 $\rho_{12}=\rho_{13}=\rho_{21}=\rho_{23}=\rho_{31}=\rho_{32}=0$.

在这 7 种情况下, 为简化计算过程, 我们将外生变量的系数均设置为 $\beta=(0.3,0.5,0.7)^T$.

噪声分布 我们考虑了不同类型的噪声分布. 首先, 我们考虑了对于同一类型的所有节点的误差有相同的方差. 特别地, 此时又考虑了方差相同时误差项的两种分布情况: (1) 正态分布: 令 $\varepsilon_{1,i_{1}}(1\leqslant i_1\leqslant n_1)$、$\varepsilon_{2,i_{2}}(1\leqslant i_2\leqslant n_2)$ 和 $\varepsilon_{3,i_{3}}(1\leqslant i_3\leqslant n_3)$ 分别表示类型 I、II、III 三种类型节点的误差, 他们分别独立同分布地从 $N(0,\sigma_1^2)$、$N(0,\sigma_2^2)$ 和 $N(0,\sigma_3^2)$ 中产生; (2) 指数分布: 令 $\varepsilon_{1,i_{1}}(1\leqslant i_1\leqslant n_1)$、$\varepsilon_{2,i_{2}}(1\leqslant i_2\leqslant n_2)$ 和$\varepsilon_{3,i_{3}}(1\leqslant i_3\leqslant n_3)$ 分别从参数为 $\lambda_1$、$\lambda_2$ 和 $\lambda_3$ 的指数分布中产生, 这也表明了 I、II 和 III 类型节点的标准差分别为 $1/\lambda_1$、$1/\lambda_2$ 和 $1/\lambda_3$.

所有的误差项都经过了中心化处理. 具体考虑两种情形: (1) 同类型节点的误差标准差相同: 假定 $\sigma_1^2=0.75$, $\sigma_2^2=1$, $\sigma_3^2=1.25$, $\lambda_1=0.75$, $\lambda_2=1$, $\lambda_3=1.25$, 那么对于同一类型节点而言, 误差项均来自于同一分布且标准差相同; (2) 同类型节点的误差标准差不同: 仅以误差项的分布为正态分布为例, 对于 $j_1(1 \leqslant j_1 \leqslant 3)$ 类型的节点中的某一个节点 $i$, 它的误差项 $\varepsilon_{j_1,i}$ 的方差 $\sigma_{j_1,i}^2(1 \leqslant i \leqslant n_{j_1})$ 是从一个均匀分布 $U(0.5,1.5)$ 中随机产生的.

我们考虑了不同大小的网络规模, $N=2000,3000,4000$. 对每一次模拟, 设置重复次数为 $M=50$ 次, 并在每一次实验中对两种方法进行了对比. 对于第 $m (1\leqslant m\leqslant M)$ 次实验, 我们用 $\hat{\rho}^{(m)}$ 来表示第 $m$ 次实验的参数 $\rho$ 估计值, 用 $\rho$ 表示真值, 用 $\hat{SE}^{(m)}$ 表示每次实验的理论标准差, 用 $CI^{(m)}$ 表示每一次实验的 95$\%$ 置信区间, 用 CP 表示收敛概率, 计算如下指标:

其中, $z_{\alpha}$ 表示标准正态分布的 $\alpha$ 下分位数, $I(\cdot)$ 为示性函数.

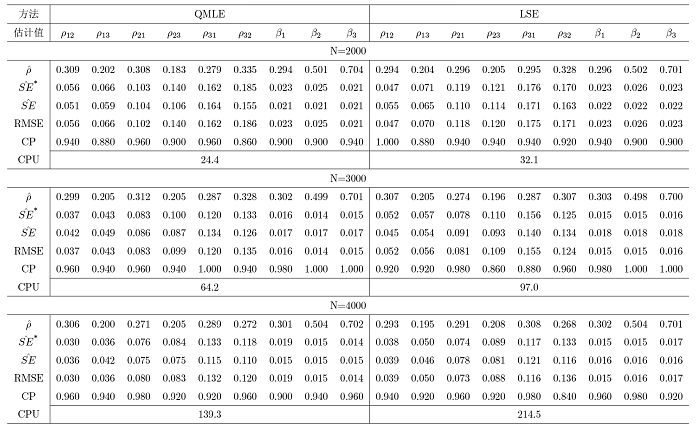
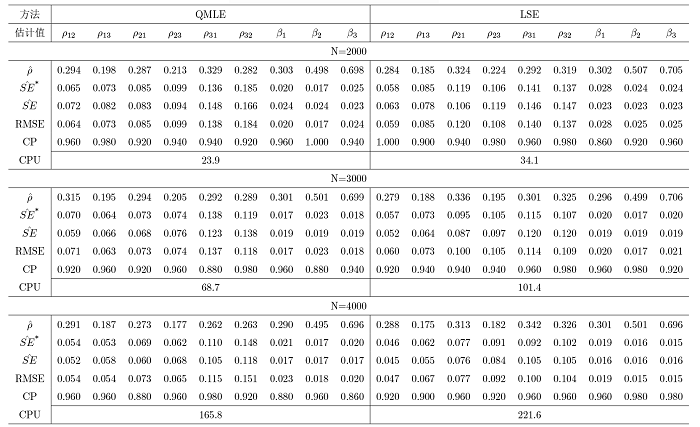
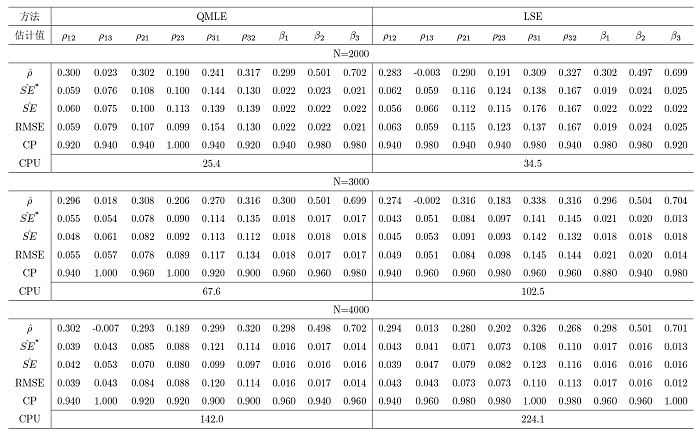
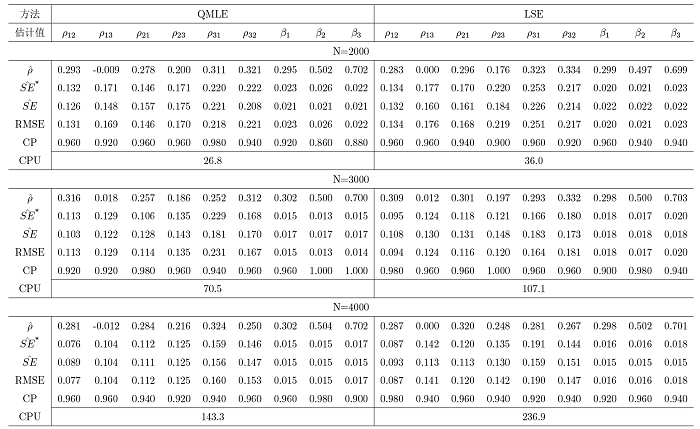
其他参数的 $\hat{SE}$、$SE^*$、RMSE、CP 均可采用相同的方式进行计算. 最后, 为了比较 QMLE 和 LSE 两种估计的效率, 在重复 50 次试验下, 对于相同情形下的试验记录并比较了各种同等网络规模下的两种方法计算的平均 CPU 时间.

表1 展示了权重矩阵采用行标准化的方式获得, 同类型节点的误差项来自相同方差的正态分布时的 1 种情形; 表2 展示了权重矩阵采用行标准化的方式获得, 同类型节点的误差项来自相同方差的指数分布时的 1 种情形; 表 3 展示了权重矩阵采用行标准化的方式获得, 同类型节点的误差项来自不同方差的正态分布时的 1 种情形; 表 4 展示了权重矩阵采用特征值标准化的方式获得, 同类型节点的误差项来自相同方差的正态分布时的 1 种情形; 对于每种设置下的其余 6 种情况, 本文均进行了模拟验证, 由于篇幅限制, 结果不再列出, 同时对于模拟的结果均进行了记录, 以及验证了每一组实验的所有参数估计结果是否满足模型的可识别性条件, 发现所有实验的参数估计结果均满足模型的可识别性条件, 进而验证了模型可识别性条件的合理性.

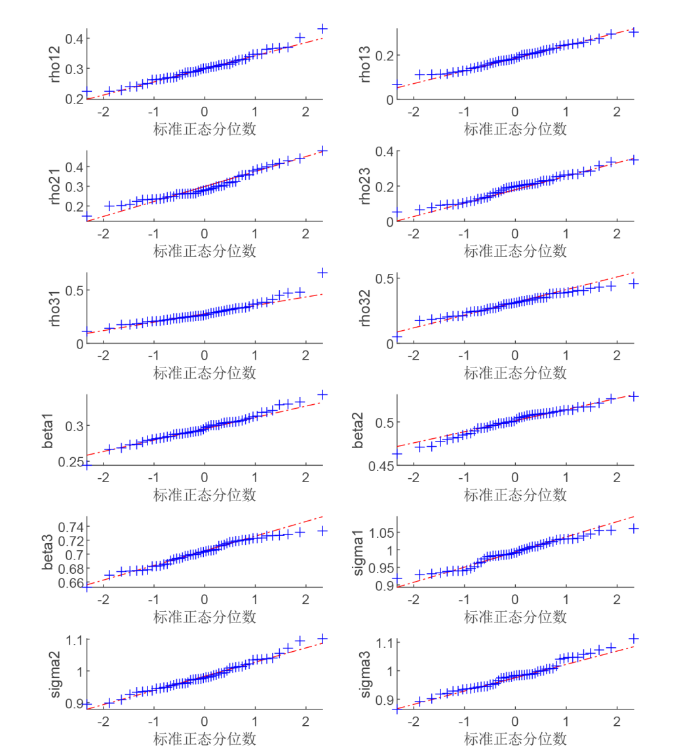
为了验证参数的渐近正态性, 本文绘制了 QQ 图, 由于篇幅的限制, 本文仅展示了表 1 中 $N=4000$ 时 QMLE 方法所估计的$\theta$中的 12 个参数的 QQ 图, 如图1 所示.

观察发现, 模拟结果在不同的交叉效应设置下是相似的, 并得到如下结论: (1) 对于所有规模的网络而言, 两种方法的参数估计值与真值都十分接近; (2) 随着网络规模 $N$ 的增大, 所有估计值的 $\hat{SE}^*$ 与 $\hat{SE}$ 都随之下降, 显示出了 QMLE 和 LSE 两种估计方法的一致性; (3) 所有参数的收敛概率都比较高, 都稳定在 90% 左右或者 90% 以上, 同时所有参数的渐近正态性均满足.

通过结论表明了真实的标准差可以通过上一章节中推导出的 QMLE 与 LSE 两种方法的理论标准差来进行近似代替, 同时当网络的规模更大时, 估计效果更好, 因为此时可以更好地减少模型中存在的内生性影响.

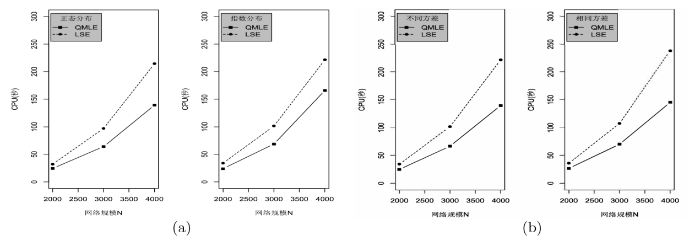
为了比较 QMLE 与 LSE 两种方法的计算效率, 图2 展示了表 1 和表 2 中两种估计方法以及相应理论标准差的平均计算时间. 通过结果, 我们可以得到如下结论: (1) 在三模 NAR 模型中, LSE 方法的计算效率比 QMLE 的计算效率差, 这与两种方法的效率的常见情况一致, 但这与双模网络自回归模型中两种估计方法的结论截然相反, 可能的原因是估计量的计算细节的不同, 比如, 二维 NAR 模型中 QMLE 与 LSE 方法的计算均采用了牛顿法, 而三维 NAR 模型中由于参数过多, QMLE 与 LSE 方法若使用牛顿法会因为 Hessian 非正定而使得牛顿法失效, 所以均采用了拟牛顿法的 BFGS 算法; (2) 随着网络规模 $N$ 的增大, QMLE 与 LSE 两种估计方法的计算效率差异越来越大, QMLE 的计算效率有明显的优势.

由于我们在记录平均计算时间的过程中既考虑了参数的估计过程, 又同时考虑了相应参数理论标准差的计算过程, 使得 QMLE 的计算效率有了一定的优势, 这也是由于采用 LSE 方法计算参数与理论标准差的过程中, 虽然避免了计算大型矩阵行列式的值, 但涉及到的矩阵形式、矩阵的逆等的形式更为复杂, 从而产生了这样的结果.

在本节, 通过考虑不同年龄段的电影评分数据, 我们讨论了三模 NAR 模型的应用. 我们对数据集构建了网络结构, 利用三模 NAR 模型的两种估计方法 QMLE 和 LSE 进行了参数估计, 并记录了两种方法的计算时间.

为了表明三模 NAR 模型的可应用性, 我们将此模型应用于 CSDN 公开的电影评分数据, 通过 2619 名 30 岁以下的观影者与 3421 名 30 岁以上的观影者对 90 年代 3883 部国外电影的评分数据构建了网络.

在这个数据中, 30 岁以下的观影者是类型 I 的节点, 30 岁以上的观影者为类型 II 的节点, 被评分的电影是类型 III 的节点, $Y_1$ 表示 30 岁以下观影者对所评分的电影的评分平均值, $Y_2$ 表示 30 岁以上观影者对所评分的电影的评分平均值, $Y_3$ 表示每部电影所得评分的平均值, 在该网络中, 网络规模记为 $N$, 三种类型的节点数目如下

对于原始网络数据, 我们首先去除了多重边, 进而通过两种类型的观影者与电影间的评分关系构建邻接矩阵为 $A=(a_{ij})$ 的三模网络, 如果对某一部电影 $k$ 而言, 如果 $a_{kj}=1$, 表示观影者 $j$ 对电影 $k$ 进行了评分, 否则 $a_{kj}=0$. 在三模 NAR 模型中, 要求网络尽可能稀疏, 本网络中, 网络密度为

说明该网络十分稀疏.

在此网络中, 由于不同年龄段的观影者之间不进行评分, 即不同年龄段的节点之间不存在边, 因而在该网络模型中邻接矩阵 $A_{12}$、$A_{21}$ 均为零矩阵, 进而权重矩阵 $W_{12}$、$W_{21}$ 也均为零矩阵, 从而构建三模 NAR 模型如下

其中, $(X_1,X_2,0)^T$ 为外生协变量, $X_1$ 和 $X_2$ 具体指性别, 我们采用这个协变量是因为评分的高低可能受到性别的影响. 若观影者为男性, 令 $X_1=1$; 若观影者为女性, 令 $X_1=2$.

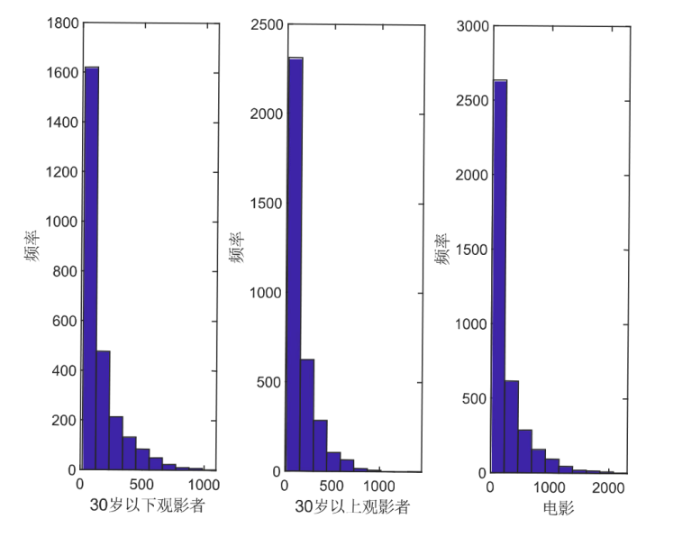
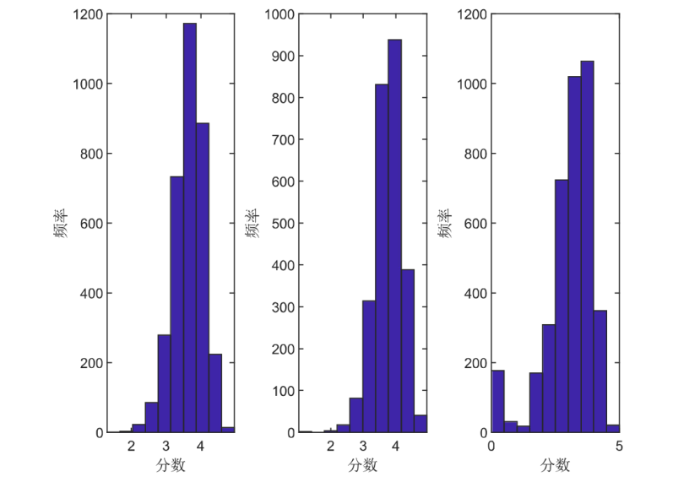
为了进一步研究该网络的结构, 我们计算了每一个类型节点的度, 即每一个类型观影者评价电影的数量或电影受到评分的数量. 例如, 类型 I 节点的度可以定义为每一位 30 岁以下的观影者所评价电影的数量, 类型 II 节点的度可以类似定义为每一位 30 岁以上的观影者所评价电影的数量, 类型 III 节点的度可以定义为每一部电影所收到的评分的数量. 三种类型节点的度的直方图通过图3 展示. 观察图3, 发现大多数节点的度都在 1000 以下, 同时 30 岁以上观影者对于 90 年代电影的评分数目相较于 30 岁以下观影者对于电影的评分数目而言更为活跃. 为了更直观展现三种类型节点的分数水平, 绘制了直方图, 如图4 所示.观察图4, 发现 30 岁以上观影者给电影的分数比 30 岁以下观影者给电影的分数较高, 说明了 30 岁以下观影者对于影片的要求较高; 而电影的分数大多集中在 4 分左右, 也不乏存在一些吸引力不高的电影使得观影者对此评分为 0.

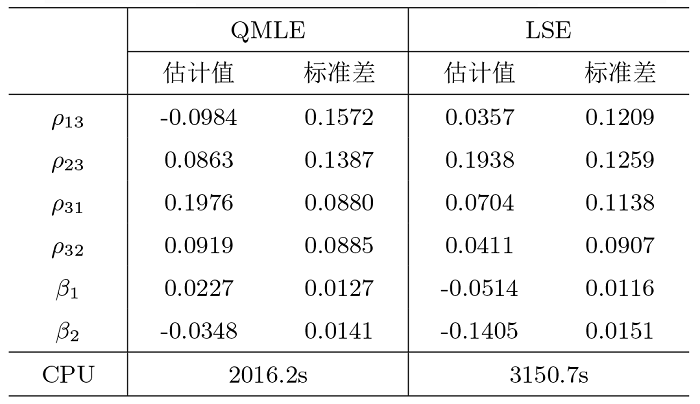
最后, 我们分别对该三模 NAR 模型用 QMLE 和 LSE 两种方法进行了拟合, 并记录了参数估计的时间, 如表5 所示. 结果显示了对三模 NAR 模型参数估计时利用 QMLE 与 LSE 两种方法的可靠性, 电影评分数据明显受到了性别的影响, 通过 CPU 的记录, 进一步验证在三模 NAR 模型中 QMLE 方法的估计效率优于 LSE 估计方法.

本文在双模 NAR 模型的基础上, 进一步研究了三模 NAR 模型. 该模型考虑了在一个十分稀疏的社交网络中, 存在三种类型节点的情况下, 对于自回归模型参数估计及其性能评估的影响. 在本文中, 我们首先介绍了一些网络、自回归模型等相关知识, 进而提出了三模 NAR 模型的定义及表示形式, 然后证明了其可逆性及参数可识别性. 在参数估计方面, 采用了 QMLE 与基于 BLP 的 LSE 两种估计方法, 并给出了估计量的渐近正态性与相合性, 数值结果表明两种估计方法的估计效果都比较好, 但 QMLE 的运算时间更快一些, 其运算时间的结论与两模 NAR 模型中的结论形成了差异.

本文中, 考虑的三模网络要求同类型的节点之间不能够相连, 但在实际网络中, 三种类型节点构成的网络也会允许同类型的节点之间产生联系, 我们可以对三模 NAR 模型进行泛化, 引入同类型节点的影响效应, 从而使得模型更加适应实际数据. 同时, 在研究三模 NAR 模型的过程中, 本文假设了三种类型的节点数目 $n_1$、$n_2$、$n_3$ 均具有相同的阶数, 所建立的参数的渐近正态性与相合性都是以此为基础建立的, 在实际中, $n_1$、$n_2$、$n_3$ 可能并不具有相同的阶数, 进而参数的渐近正态性与相合性可能会发生变化, 未来可以从这一角度对此进行推广研究.

其中, $\Omega_e=\Sigma_e^{-1}$,$1 \leq j_1\neq j_2 \leq 3,1 \leq k \leq 3$.

其中,

根据文献[22]得

其中 $\Sigma_{i,(-i)} \in R^{1\times(N-1)}$ 是 $\Sigma$ 的第 $i$ 行但不包含第 $i$ 列, $\Sigma_{(-i),(-i)} \in R^{(N-1)\times(N-1)}$ 是 $\Sigma$ 但不包含第 $i$ 个行和第 $i$ 列. 利用 $\Omega=\Sigma^{-1}$ 与 $\Sigma=(\textbf{I}_{N}-\textbf{W}_{\rho})^{-1}\Sigma_e(\textbf{I}_{N}-\textbf{W}_{\rho}^T)^{-1}$, 通过代数计算得$\Sigma_{i,(-i)}=-\Omega_{i,i}^{-1}\Omega_{i,(-i)}(\Omega_{(-i),(-i)}-\Omega_{i,(-i)}^T\Omega_{i,i}^{-1}\Omega_{i,(-i)})^T,\Sigma_{(-i),(-i)}^{-1}=\Omega_{(-i),(-i)}-\Omega_{i,(-i)}^T\Omega_{i,i}^{-1}\Omega_{i,(-i)}.$因此, 可以得到 $\mathcal{F}\{\tilde{Y}_{(i)}|\tilde{Y}_{(-i)}\}=-\Omega_{i,i}^{-1}\Omega_{i,(-i)}\tilde{Y}_{(-i)}.$

回顾 $\Omega=\Sigma^{-1}=\Sigma_e^{-1}-\Sigma_e^{-1}W_{\rho}-W_{\rho}^{T}\Sigma_e^{-1}+W_{\rho}\Sigma_e^{-1}W_{\rho}^T$, 如果 $j_1,j_2,j_3 \in \{1,2,3\},$$i\in N_j,$$j_1 \neq j_2 \neq j_3$, 有

$\begin{align*} \Omega=& \begin{pmatrix} \sigma_1^{-2}\textbf{I}_{n_1} & \textbf{0} & \textbf{0} \\ \textbf{0} & \sigma_2^{-2}\textbf{I}_{n_2} & \textbf{0}\\\textbf{0} & \textbf{0} & \sigma_3^{-2}\textbf{I}_{n_3}\end{pmatrix} -\begin{pmatrix} \sigma_1^{-2}\textbf{I}_{n_1} & \textbf{0} & \textbf{0} \\ \textbf{0} & \sigma_2^{-2}\textbf{I}_{n_2} & \textbf{0}\\\textbf{0} & \textbf{0} & \sigma_3^{-2}\textbf{I}_{n_3}\end{pmatrix}\begin{pmatrix} \textbf{0} & \rho_{12}W_{12}& \rho_{13}W_{13} \\ \rho_{21}W_{21} & \textbf{0}\rho_{23}W_{23}\\\rho_{31}W_{31}& \rho_{32}W_{32}& \textbf{0} \end{pmatrix}\\&-\begin{pmatrix} \textbf{0} & \rho_{12}W_{12}^T& \rho_{13}W_{13}^T \\ \rho_{21}W_{21}^T & \textbf{0}& \rho_{23}W_{23}^T\\\rho_{31}W_{31}^T& \rho_{32}W_{32}^T& \textbf{0} \end{pmatrix}\begin{pmatrix} \sigma_1^{-2}\textbf{I}_{n_1} & \textbf{0} & \textbf{0} \\ \textbf{0} & \sigma_2^{-2}\textbf{I}_{n_2} & \textbf{0}\\\textbf{0} & \textbf{0} & \sigma_3^{-2}\textbf{I}_{n_3}\end{pmatrix} +\begin{pmatrix} \textbf{0} & \rho_{12}W_{12}& \rho_{13}W_{13} \\ \rho_{21}W_{21} & \textbf{0}& \rho_{23}W_{23}\\\rho_{31}W_{31}& \rho_{32}W_{32}& \textbf{0} \end{pmatrix}\\ & \quad \begin{pmatrix} \sigma_1^{-2}\textbf{I}_{n_1} & \textbf{0} & \textbf{0} \\ \textbf{0} & \sigma_2^{-2}\textbf{I}_{n_2} & \textbf{0}\\\textbf{0} & \textbf{0} & \sigma_3^{-2}\textbf{I}_{n_3}\end{pmatrix} \begin{pmatrix} \textbf{0} & \rho_{12}W_{12}^T& \rho_{13}W_{13}^T \\ \rho_{21}W_{21}^T & \textbf{0}& \rho_{23}W_{23}^T\\\rho_{31}W_{31}^T& \rho_{32}W_{32}^T& \textbf{0} \end{pmatrix} =\begin{pmatrix} { \omega_{11} } & { \omega_{12} } & { \omega_{13} }\\ { \omega_{21} } & { \omega_{22} } & { \omega_{23} }\\ { \omega_{31} } & { \omega_{32} } & { \omega_{33} } \end{pmatrix}, \end{align*}$

其中

进而得到: 若 $i \in N_j, j_1,j_2,j_3 \in \{1,2,3\}, j_1 \neq j_2 \neq j_3$, 有

其中$w_{ki}$ 表示 $W$ 的第 $(k,i)$ 个元素, $\alpha_i=\Sigma_{k \in \mathcal{N}_{j_{2}}}w_{ki}^2$ 和 $\beta_i=\Sigma_{k \in \mathcal{N}_{j_{3}}}w_{ki}^2$. 引理得证.

其中,