非定常 Stokes/Darcy 模型一种新的time filter 算法的分析

图 1 全局域 $\Omega$ 由被交界面 $\Gamma$ 分隔开的自由流体区域 $\Omega_f$ 和多孔介质区域 $\Omega_p$ 构成

本文研究由 Stokes 方程和 Darcy 方程组成的 Stokes/Darcy 模型. 设 $T>0$ 是一个有限的时间. 自由流体区域 $\Omega_f$ 流动由 Stokes 方程控制: 求流体速度 ${\bf u}_f:\Omega_f\times[T]\rightarrow{\bf R}^d$ 和压力 $p_f:\Omega_f\times[T]\rightarrow{\bf R}$ 满足

$\begin{eqnarray*} \label{Stokes1}\frac{\partial {\bf u}_f}{\partial t}-\nabla\cdot({\bf T}_\nu({\bf u}_f,p_f))={\bf g}_f, \qquad &&\mbox{在}\;\Omega_f\times(0,T]\ \mbox{中}\;,\end{eqnarray*}$

(2.1)

$\begin{eqnarray*} \nabla\cdot {\bf u}_f=0, \qquad\qquad\qquad\qquad\qquad&&\mbox{在}\;\Omega_f\times(0,T] \ \mbox{中}\;, \end{eqnarray*}$

(2.2)

其中

${\bf T}_\nu({\bf u}_f,p_f)=-p_f{\bf I}+2\nu{\bf D}({\bf u}_f),\quad {\bf D}({\bf u}_f)=\frac12(\nabla {\bf u}_f+\nabla^Tu_f),$

分别是应力张量和应变张量, $\nu>0$ 是粘性系数, ${\bf g}_f({\bf x},t)$ 是外力项.

多孔介质区域 $\Omega_p$ 流动由以下方程控制

$\begin{matrix} \label{Darcy1}&&\frac{S\partial\phi_p}{\partial t}+\nabla\cdot {\bf u}_p={\bf g}_p, \qquad\qquad\qquad\ \mbox{在}\;\Omega_p\times(0,T]\ \mbox{中}\;,\end{matrix}$

(2.3)

$\begin{matrix} \label{Darcy2}&&{\bf u}_p=-{\bf K}\nabla\phi_p, \qquad\qquad\qquad\qquad\quad\mbox{在}\;\Omega_p\times(0,T]\ \mbox{中}\;, \end{matrix}$

(2.4)

其中, 第一个方程是饱和流动模型, $S$ 是比质量储能系数, $\phi_p=z+\frac{p_p}{\rho g}$ 是测压水头, $p_p$ 表示流体在 $\Omega_p$ 中的压力, $z$ 是从参考平面算起的高度, $\rho$ 和 $g$ 分别表示密度和重力加速度. 第二个方程是 Darcy 定律, ${\bf u}_p$ 是多孔介质区域 $\Omega_p$ 的流体速度, 与 $\phi_p$ 的梯度成正比关系. ${\bf K}$ 表示水利传导率张量, 它是一个最小特征值大于零的对称正定的矩阵, 且允许在空间中变化. ${\bf g}_p({\bf x},t)$ 是源项.

将方程(2.4)代入方程(2.3)可得 Darcy 方程: 求测压水头 $\phi_p:\Omega_p\times[T]\rightarrow{\bf R}^d$ 满足

$\begin{equation}\label{Darcy} \frac{S\partial\phi_p}{\partial t}-\nabla\cdot({\bf K}\nabla\phi_p)={\bf g}_p,\qquad\mbox{在}\;\Omega_p\times(0,T]\ \mbox{中}\;. \end{equation}$

(2.5)

下面考虑 Stokes/Darcy 模型满足以下初值条件

${\bf u}_f(x,0)={\bf u}_f^0(x),\qquad\mbox{在}\;\Omega_f\ \mbox{中}\;.$

(2.6)

$\phi_p(x,0)=\phi_p^0(x),\qquad\mbox{在}\;\Omega_p\ \mbox{中}\;.$

(2.7)

以及齐次 Dirichlet 边界条件

$\label{boundary} {\bf u}_f=0, \qquad\mbox{在}\;\Gamma_f\ \mbox{上}\;.$

(2.8)

$\phi_p=0,\qquad\mbox{在}\;\Gamma_p\ \mbox{上}\;.$

(2.9)

交界面条件是 Stokes/Darcy 模型的重要组成部分, 包括质量守恒条件, 法向力的平衡条件和 Beavers-Joseph-Saffman(BJS) 条件. 具体表示如下: 在 $\Gamma$ 上满足

$\begin{equation}\label{BJ} \left\{\begin{array}{l} {\bf u}_f\cdot {\bf n}_f-{\bf K}\nabla\phi_p\cdot {\bf n}_p=0,\\ -[{\bf T}_\nu({\bf u}_f,p_f)\cdot {\bf n}_f]\cdot {\bf n}_f=g\phi_p,\\ -[{\bf T}_\nu({\bf u}_f,p_f)\cdot {\bf n}_f]\cdot {\boldsymbol{\tau}}_i=\frac{\alpha\nu\sqrt{d}}{\sqrt{\mbox{trace}({\bf \Pi})}}{\bf u}_f\cdot {\boldsymbol{\tau}}_i. \end{array}\right. \end{equation}$

(2.10)

其中 ${\boldsymbol{\tau}}_i$ , $i=1,2,\cdots,d-1$ , 是沿着 $\Gamma$ 的正交切向单位向量, $\alpha$ 是一个确定的实验参数, ${\bf \Pi}$ 表示渗透率, 与水利传导率张量存在关系: ${\bf K}=\frac{{\bf \Pi}g}{\nu}$ .

首先定义 Hilbert 空间

$\begin{eqnarray*} &&{\bf H}_f=\{{\bf v}_f \in ({\bf H}^1(\Omega_f)^d): {\bf v}_f|_{\Gamma_f}=0\},\\ &&{\bf H}_p=\{\psi_p\in ({\bf H}^1(\Omega_p)^d): \psi_p|_{\Gamma_p}=0\},\\ &&Q_f=L^2(\Omega_f),\\ &&{\bf U}={\bf H}_f\times {\bf H}_p. \end{eqnarray*}$

区域 $D$ 中, $(\cdot,\cdot)_D$ 表示 $D=\Omega_f$ 或 $\Omega_p$ 中的内积. 并对空间 ${\bf U}$ 配备以下范数: $\forall$ $\underline{\bf u}=({\bf u}_f,\phi_p)\in {\bf U}$ ,有

$\begin{eqnarray*} &&\|\underline{\bf u}\|_0=\sqrt{({\bf u}_f,{\bf u}_f)_{\Omega_f}+gS(\phi_p,\phi_p)_{\Omega_p}}\,\\ &&\|\underline{\bf u}\|_{\bf U}=\sqrt{\nu(\nabla {\bf u}_f,\nabla {\bf u}_f)_{\Omega_f}+g{\bf K}(\nabla\phi_p,\nabla\phi_p)_{\Omega_p}}. \end{eqnarray*}$

用 $\Vert\cdot\Vert_{{\bf H}_f/{\bf H}_p}$ , $\Vert\cdot\Vert_{f/p}$ 和 $\Vert\cdot\Vert_{\Gamma}$ 分别表示范数 ${\bf H}^1(\Omega_{f/p})$ , $L^2(\Omega_{f/p})$ , $L^2(\Gamma)$ . 同时定义下列范数

$\begin{eqnarray*} &&\Vert {\bf u}_f\Vert_f=\Vert {\bf u}_f\Vert_{L^2(\Omega_f)},\ \ \Vert {\bf u}_f\Vert_{{\bf H}_f}=\Vert\nu^{\frac{1}{2}}\nabla u_f\Vert_{L^2(\Omega_f)},\\ &&\Vert\phi_p\Vert_p=\Vert\phi_p\Vert_{L^2(\Omega_p)}, \Vert\phi_p\Vert_{{\bf H}_p}=\Vert{\bf K}^{\frac{1}{2}}\nabla\phi_p\Vert_{L^2(\Omega_p)}. \end{eqnarray*}$

对函数 $v(x,t)$ 定义范数

$\|v\|_{L^2(0,T;L^2)}:=(\int_{0}^{T}\|v(\cdot,t)\|_{L^2}^2{\rm d}t)^{\frac{1}{2}},\quad \|v\|_{L^2(0,T;L^{\infty})}:=ess\sup_{[T]}\|v(\cdot,t)\|_{L^2}.$

其次, 非定常Stokes/Darcy 耦合模型(2.1)-(2.10)式的弱形式描述如下: 对于 ${\bf g}_f\in L^2(0,T; {\bf L}^2(\Omega_f))$ , ${\bf g}_p\in L^2(0,T; {\bf L}^2(\Omega_p))$ , 求 $\underline{\bf u}=(u_f, \phi_p) \in (L^2(0,T; {\bf H}_f)\cap L^\infty(0,T; L^2(\Omega_f)) \times L^2(0,T; {\bf H}_p)\cap L^\infty(0,T; L^2(\Omega_p)) )$ 和 $p_f\in L^2(0,T; Q_f)$ 使得 $\forall$ $(\underline{\bf v},q_f) \in{\bf U}\times Q_f$ 满足

$\begin{matrix}\label{coupled} &&(\frac{\partial\underline{\bf u}}{\partial t},\underline{\bf v})+a(\underline{\bf u},\underline{\bf v})+b(\underline{\bf v},p_f)=\langle {\bf F},\underline{\bf v} \rangle_{\bf U'},\nonumber\\ &&b(\underline{\bf u},q_f)=0,\\ &&\underline{\bf u}(\bf x,0)=\underline{\bf u}^0,\nonumber \end{matrix}$

(2.11)

其中

$\begin{eqnarray*} &&(\frac{\partial\underline{\bf u}}{\partial t},\underline{\bf v})=(\frac{\partial {\bf u}_f}{\partial t},{\bf v}_f)+g(\frac{S\partial\phi_p}{\partial t},\psi_p),\\ &&a(\underline{\bf u},\underline{\bf v})=a_{\Omega}(\underline{\bf u},\underline{\bf v})+a_\Gamma(\underline{\bf u},\underline{\bf v}),\\ &&a_{\Omega}(\underline{\bf u},\underline{\bf v})=a_{\Omega_f}({\bf u}_f,{\bf v}_f)+a_{\Omega_p}(\phi_p,\psi_p),\\ &&a_{\Omega_f}({\bf u}_f,{\bf v}_f)=\nu({\bf D}({\bf u}_f),{\bf D}({\bf v}_f))_{\Omega_f} +(\displaystyle{\frac{\alpha\nu\sqrt{d}}{\sqrt{\mbox{trace}({\bf \Pi})}}}P_{\tau}({\bf u}_f,{\bf v}_f))_\Gamma,\\ &&a_{\Omega_p}(\phi_p,\psi_p)=g({\bf K}\nabla\phi_p,\nabla\psi_p)_{\Omega_p},\\ &&a_\Gamma(\underline{\bf u},\underline{\bf v})=c_{\Gamma}({\bf v}_f,\phi_p)-c_{\Gamma}({\bf u}_f,\psi_p)= g(\phi_p,{\bf v}_f\cdot {\bf n}_f)_\Gamma-g(\psi_p,{\bf u}_f\cdot {\bf n}_f)_\Gamma,\\ &&b(\underline{\bf v},p_f)=-(p_f,\nabla\cdot {\bf v}_f)_{\Omega_f},\\ &&\langle {\bf F},\underline{\bf v}\rangle_{{\bf U}'}=({\bf g}_f,{\bf v}_f)_{\Omega_f}+g({\bf g}_p,\psi_p)_{\Omega_p}. \end{eqnarray*}$

${\bf U}'$ 是 ${\bf U}$ 的对偶空间, $P_{\tau}(\cdot)$ 是局部切平面上的投影, 表示为 $P_{\tau}({\bf v}_f)={\bf v}_f-({\bf v}_f\cdot{\bf n}_f){\bf n}_f$ .

双线性形式 $a(\cdot,\cdot)$ 满足连续性和强制性: $\forall$ $\underline{\bf u}, \underline{\bf v}\in {\bf U},$ ${\bf u}_f\in {\bf H}_f,$ $\phi_p \in {\bf H}_p,$ 有

$\begin{eqnarray*} &&a(\underline{\bf u},\underline{\bf v})\leq C_{con} \|\underline{\bf u}\|_{\bf U}\|\underline{\bf v}\|_{\bf U},\\ && a(\underline{\bf u},\underline{\bf u})\geq C_{coe} \|\underline{\bf u}\|_{\bf U}^2, \\ &&a_{\Omega_f}({\bf u}_f,{\bf u}_f)\geq \hat{C}_{coe} \|{\bf u}_f\|_{{\bf H}_f}^2,\\ &&a_{\Omega_p}(\phi_p,\phi_p)\geq \check{C}_{coe} \|\phi_p\|_{{\bf H}_p}^2. \end{eqnarray*}$

$a_\Gamma(\cdot,\cdot)$ 满足反对称性

$\begin{matrix}\label{c} a_\Gamma(\underline{\bf u},\underline{\bf v})=-a_\Gamma(\underline{\bf v},\underline{\bf u}),\quad\quad a_\Gamma(\underline{\bf u},\underline{\bf u})=0, \quad\forall\ \underline{\bf u},\underline{\bf v}\in {\bf U}. \end{matrix}$

(2.12)

下面给出Poincar $\acute{e}$ , Trace, Sobolev 不等式: 存在常数 $C_p$ , $C_t$ 和 $C_s$ 仅仅依赖于区域 $\Omega_f$ , $\tilde{C}_p$ , $\tilde{C}_t$ 和 $\tilde{C}_s$ 仅仅依赖于区域 $\Omega_p$ , 使得 $\forall$ ${\bf v}_f\in{\bf H}_f$ 和 $\psi_p\in{\bf H}_p$ ,有

$\begin{matrix}\label{pts} &&\|{\bf v}_f\|_{f}\leq C_p\|\nabla{\bf v}_f\|_{f},\qquad\qquad\qquad\quad \|\psi_p\|_{f}\leq \tilde{C}_p\|\nabla\psi_p\|_{p},\nonumber\\ &&\|{\bf v}_f\|_{\Gamma}\leq C_t\|\nabla{\bf v}_f\|_{f},\qquad\qquad\qquad\quad \|\psi_p\|_{\Gamma}\leq \tilde{C}_t\|\nabla\psi_p\|_{p},\\ &&\|{\bf v}_f\|_{H^\frac{1}{2}(\partial\Omega_f)}\leq C_s\|\nabla{\bf v}_f\|_{f},\qquad\qquad\|\psi_p\|_{H^\frac{1}{2}(\partial\Omega_p)}\leq \tilde{C}_s\|\nabla\psi_p\|_{p}.\nonumber \end{matrix}$

(2.13)

定常的耦合Stokes/Darcy 模型的适定性已被证明. 这里, 假定在非稳态的情况下也同样成立. 本文主要研究其数值解.

3 数值算法和稳定性

对任意给定的小参数 $h>0$ , 构造 $\Omega$ , $\Omega_f$ 和 $\Omega_p$ 的正则三角剖分 ${\cal T}_h$ , ${\cal T}_{fh}$ 和 ${\cal T}_{ph}$ . 为了简便, 设 $\Omega_f$ 和 $\Omega_p$ 是足够光滑的区域. 通过 MINI 元 (P1b-P1) 离散的 ${\bf H}_{fh}\subset{\bf H}_f$ , $Q_{fh}\subset Q_f$ 和通过线性拉格朗日元 (P1) 离散的 ${\bf H}_{ph}\subset {\bf H}_p$ 是有限元空间, 使得空间对 $({\bf H}_{fh},Q_{fh})$ 满足离散的 LBB 条件

$\begin{equation}\label{DLBB} \inf\limits_{q_{fh}\in Q_{fh}}\sup\limits_{{\bf v}_{fh}\in {\bf H}_{fh}}\frac{(q_{fh},\nabla\cdot {\bf v}_{fh})_{\Omega_f}}{\|q_{fh}\|_{Q_f}\,\|{\bf v}_{fh}\|_{{\bf H}_f}}\geq \beta, \end{equation}$

(3.1)

并定义 ${\bf u}_h={\bf H}_{fh}\times {\bf H}_{ph}$ .

定义线性投影算子(见文献[31]): $\forall$ $\underline{\bf v}_h\in{\bf u}_h$ , $q_{fh}\in Q_{fh}$ 和 $t\in(0,T]$ , $P_h:(\underline{\bf u}(t),p_f(t)) \in {\bf U}\times Q_f\to(P_h^{\underline{\bf u}}\underline{\bf u}(t), P_h^{p}p_f(t)) \in {\bf u}_h\times Q_{fh}$ 满足

$\begin{eqnarray*}\label{projection} &&a(P_h^{\underline{\bf u}}\underline{\bf u}(t),\underline{\bf v}_h)+b(\underline{\bf v}_h,P_h^{p}p_f(t))=a(\underline{\bf u}(t),\underline{\bf v}_h)+b(\underline{\bf v}_h,p_f(t)),\\\nonumber &&b(P_h^{\underline{\bf u}}\underline{\bf u}(t),q_{fh})=0. \end{eqnarray*}$

(3.2)

假设 $(\underline{\bf u}(t),p_f(t))$ 足够光滑, $(\underline{\bf u}(t),p_f(t))$ 的投影 $(P_h^{\underline{\bf u}}\underline{\bf u}(t)$ , $P_h^{p}p_f(t))$ 满足性质

$\begin{matrix}\label{app} &&\|P_h^{\underline{\bf u}}\underline{\bf u}(t)-\underline{\bf u}(t)\|_0\leq Ch^2\|\underline{\bf u}(t)\|_{H^2},\nonumber\\ &&\|P_h^{\underline{\bf u}}\underline{\bf u}(t)-\underline{\bf u}(t)\|_{\bf U}\leq Ch\|\underline{\bf u}(t)\|_{H^2},\\ &&\|P_h^{p}p_f(t)-p_f(t)\|_{L^2}\leq Ch\|p_f(t)\|_{H^1}.\nonumber \end{matrix}$

(3.3)

Inverse 不等式: 存在常数 $C_I$ , $\tilde{C}_I$ 依赖于有限元网格中的角度, 使得 $\forall$ ${\bf v}_{fh}\in{\bf H}_{fh}$ , $\psi_{ph}\in {\bf H}_{ph}$ ,

$\begin{matrix}\label{inverse} \|{\bf v}_{fh}\|_{{\bf H}_f}\leq C_I h^{-1}\|{\bf v}_{fh}\|_{f},\qquad \|\psi_{ph}\|_{{\bf H}_p}\leq \tilde{C}_I h^{-1}\|\psi_{ph}\|_{p}. \end{matrix}$

(3.4)

理论分析时将用到下面两个引理.

${\bf引理3.1}$ (文献[30,第4章引理 3.3]) 设 $\delta =\beta_2-\frac{\alpha_2}{2}>0$ . 系数 $\alpha_i$ 和 $\beta_i$ 满足下面关系

$\begin{eqnarray*} 2\bigg(\sum_{i=0}^{2}\alpha_i\zeta_i\bigg) \bigg(\sum_{i=0}^{2}\beta_i\zeta_i\bigg) &\geq &(\alpha_2^2+\delta )\zeta_2^2-(2\alpha_2-1)\zeta_1^2-\left((\alpha_2-1)^2+\delta\right)\zeta_0^2\\ &&-2\left(\alpha_2(\alpha_2-1)+\delta\right)(\zeta_2\zeta_1-\zeta_1\zeta_0),\quad \forall\ \zeta_0, \zeta_1, \zeta_2\in R. \end{eqnarray*}$

${\bf引理3.2}$ (文献[引理 1]) $\forall$ ${\bf v}_f\in {\bf H}_f$ , $\phi_p\in{\bf H}_p$ , 存在 $C_k>0$ , 使得 $\forall$ $\varepsilon>0$ ,有

$\begin{matrix}\label{Gammal} \vert c_\Gamma({\bf v}_f,\phi_p)\vert \leq\frac{1}{4\varepsilon}\Vert {\bf v}_f \Vert_{{\bf H}_f}^2 +C\varepsilon\Vert\phi_p\Vert_{{\bf H}_p}^2. \end{matrix}$

(3.5)

另外, $\forall$ ${\bf v}_{fh}\in {\bf H}_{fh}$ , $\phi_{ph}\in{\bf H}_{ph}$ , 存在 $\tilde{C}_k>0$ , 使得 $\forall$ $\tilde{\varepsilon}>0$ , 有

$\begin{matrix}\label{Gamma2} \vert c_\Gamma({\bf v}_{fh},\phi_{ph})\vert \leq\frac{1}{4\tilde{\varepsilon}}\Vert{\bf v}_{fh}\Vert_{{\bf H}_f}^2 +C\tilde{\varepsilon} h^{-1}\Vert\phi_{ph}\Vert_{p}^2. \end{matrix}$

(3.6)

这里引入相关的记号

$\begin{eqnarray*} &&A(\underline{\bf u}_h^{m+1},\theta)= \frac{3-2\theta}{2}\underline{\bf u}_h^{m+1}-2(1-\theta)\underline{\bf u}_h^{m}+\frac{1-2\theta}{2}\underline{\bf u}_h^{m-1},\\ &&B(\underline{\bf u}_h^{m+1},\theta)=\frac{(1-\theta)(3-2\theta)}{2}\underline{\bf u}_h^{m+1} +(4\theta-1-2\theta^2)\underline{\bf u}_h^{m} +\frac{(1-\theta)(1-2\theta)}{2}\underline{\bf u}_h^{m-1},\\ &&F({\bf F}^{m+1},\theta)=-\frac{(1-\theta)(1-2\theta)}{2}{\bf F}^{m+1} +(1-\theta)(1-2\theta){\bf F}^{m} -\frac{(1-\theta)(1-2\theta)}{2}{\bf F}^{m-1},\\ &&W(\eta_{{\phi}_p}^{m+1},\theta)=(1-\theta)(3-2\theta)\eta_{{\phi}_p}^{m} -\frac{(1-\theta)(3-2\theta)}{2}\eta_{{\phi}_p}^{m-1} -\frac{(1-\theta)(3-2\theta)}{2}\eta_{{\phi}_p}^{m+1}. \end{eqnarray*}$

本节其余部分将给出非定常 Stokes/Darcy 模型耦合和解耦的线性多步法加 time filter 算法以及其稳定性. 将时间段 $[T]$ 进行均匀剖分, 并令 $t_m=m\Delta t$ , $m=0,1,\cdots,N$ , 其中 $\Delta t=\frac{T}{N}$ 是时间步长. $(\underline{\bf u}_h^{m+1},p_{fh}^{m+1})=({\bf u}_{fh}^{m+1},p_{fh}^{m+1},\phi_{ph}^{m+1})$ 表示 $(\underline{\bf u}_h(t_{m+1}), p_{fh}(t_{m+1}))=({\bf u}_{fh}(t_{m+1}),p_{fh}(t_{m+1}),\phi_{ph}(t_{m+1}))$ 的全离散格式的数值解.

3.1 耦合算法及其稳定性

耦合的线性多步法加 time filter 算法描述如下.

$\blacktriangledown$ 线性多步法 (一阶收敛)

给定 $({\underline{\bf u}}_h^0,{p}_{fh}^0)$ 和 $({\underline{\bf u}}_h^1,{p}_{fh}^1)$ , 求 $\hat{\underline{\bf u}}_h^{m+1}=(\hat{\bf u}_{fh}^{m+1}$ , $\hat{\phi}_{ph}^{m+1})\in{\bf u}_h$ , $\hat{p}_{fh}^{m+1}\in Q_{fh}$ , $m=1,2,$ $\cdots,N-1$ , 使得 $\forall$ $\underline{\bf v}_h\in{\bf u}_h$ 和 $q_{fh}\in Q_{fh}$ ,

$\begin{equation} \begin{array}{ll} \label{first} \bigg(\frac{\hat{\underline{\bf u}}_h^{m+1}-\underline{\bf u}_h^{m}}{\Delta t},\underline{\bf v}_h\bigg) +a\left((1-\theta)\hat{\underline{\bf u}}_h^{m+1}+\theta\underline{\bf u}_h^{m},\underline{\bf v}_h\right) +b\left(\underline{\bf v}_h,(1-\theta)\hat{p}_{fh}^{m+1}+\theta p_{fh}^{m}\right)\\ =\langle (1-\theta){\bf F}^{m+1}+\theta{\bf F}F^{m},\underline{\bf v}_h\rangle,\\ b\left((1-\theta)\hat{\underline{\bf u}}_h^{m+1}+\theta\underline{\bf u}_h^{m},q_{fh}\right)=0. \end{array} \end{equation}$

(3.7)

$\blacktriangledown$ Time Filter 算法 (二阶收敛)

通过 time filter 算法更新线性多步法的解 $(\hat{\underline{\bf u}}_h^{m+1},\hat{p}_{fh}^{m+1})$ ,

$\begin{equation} \begin{array}{ll} \label{tf} \underline{\bf u}_h^{m+1}=\hat{\underline{\bf u}}_h^{m+1}-\frac{1-2\theta}{3-2\theta}(\hat{\underline{\bf u}}_h^{m+1}-2\underline{\bf u}_h^{m}+\underline{\bf u}_h^{m-1}),\\[3mm] p_{fh}^{m+1}=\hat{p}_{fh}^{m+1}-\frac{1-2\theta}{3-2\theta}(\hat{p}_{fh}^{m+1}-2p_{fh}^{m}+p_{fh}^{m-1}). \end{array} \end{equation}$

(3.8)

${\bf注3.1}$ 无论压力 $\hat{p}_{fh}^{m+1}$ 是否经 time filter 更新, 最终的结论几乎一致.

下面给出耦合的线性多步法加 time filter 算法的稳定性分析.

${\bf定理3.1}$ (耦合算法的稳定性) 设 $\underline{\bf u}_h^{m+1}$ 是线性多步法加 time filter 算法的解. 对于 $N\geq 2$ , 有

$\begin{eqnarray*} &&\|\underline{\bf u}_h^{N}\|_0^2+\frac{4(1-\theta)C_{coe}\Delta t}{3-2\theta}\sum_{m=1}^{N-1} \left\|B(\underline{\bf u}_h^{m+1},\theta)\right\|_{\bf U}^2\\ &\leq &C (\|{\bf g}_{f}\|^2_{L^2(0,T;L^2(\Omega_f))}+\|{\bf g}_{p}\|^2_{L^2(0,T;L^2(\Omega_p))} +\|\underline{\bf u}_h^{1}\|^2_0+\|\underline{\bf u}_h^{0}\|^2_0+\|\underline{\bf u}_h^{1}\|_0\|\underline{\bf u}_h^{0}\|_0). \end{eqnarray*}$

其中 $C$ 是一个常数, 与 $h$ , $\Delta t$ 以及其他参数无关, 并且在不同的情况下可能取不同的值.

${\bf证}$ 由 (3.8) 式可得

$\hat{\underline{\bf u}}_h^{m+1}=\frac{3-2\theta}{2}\underline{\bf u}_h^{m+1}-(1-2\theta)\underline{\bf u}_h^{m}+\frac{1-2\theta}{2}\underline{\bf u}_h^{m-1},$

$\hat{p}_{fh}^{m+1}=\frac{3-2\theta}{2}p_{fh}^{m+1}-(1-2\theta)p_{fh}^{m}+\frac{1-2\theta}{2}p_{fh}^{m-1},$

将上述两式代入 (3.7) 式, $\forall\ \underline{\bf v}_h\in {\bf u}_h$ , $q_{fh}\in Q_{fh}$ ,有

$\begin{matrix} \label{TF} &&\frac{1}{\Delta t}\bigg(A(\underline{\bf u}_h^{m+1},\theta),\underline{\bf v}_h\bigg) +a\left(B(\underline{\bf u}_h^{m+1},\theta),\underline{\bf v}_h\right) +b\left(\underline{\bf v}_h,B(p_{fh}^{m+1},\theta)\right)\nonumber\\ &=&\langle(1-\theta){\bf F}^{m+1}+\theta{\bf F}^{m},\underline{\bf v}_h\rangle,\\ &&b\left(B(\underline{\bf u}_h^{m+1},\theta), q_{fh}\right)=0.\nonumber \end{matrix}$

(3.9)

假设 $\underline{\bf v}_h=2\Delta t B(\underline{\bf u}_h^{m+1},\theta)$ , $q_{fh}=2\Delta t B(p_{fh}^{m+1},\theta)$ , 下面对 (3.8) 式的每一项进行分析. 首先, 由于 $\frac{(1-\theta)(3-2\theta)}{2}-\frac{1}{2}\frac{3-2\theta}{2}>0$ , 因此借助引理3.1, 有

$\begin{matrix}\label{L1} &&2\left(A(\underline{\bf u}_h^{m+1},\theta),B(\underline{\bf u}_h^{m+1},\theta)\right)\nonumber\\ &\geq& (2\theta^2-5\theta+3)\|\underline{\bf u}_h^{m+1}\|^2_0 -2(1-\theta)\|\underline{\bf u}_h^{m}\|^2_0 -(1-2\theta)(1-\theta)\|\underline{\bf u}_h^{m-1}\|^2_0\nonumber\\ &&-(1-2\theta)(3-2\theta)(\|\underline{\bf u}_h^{m+1}\|_0\|\underline{\bf u}_h^{m}\|_0 -\|\underline{\bf u}_h^{m}\|_0\|\underline{\bf u}_h^{m-1}\|_0). \end{matrix}$

(3.10)

其次, 利用双线性形式 $a(\cdot,\cdot)$ 的强制性可得

$\begin{matrix}\label{L2} 2\Delta t a\left(B(\underline{\bf u}_h^{m+1},\theta),B(\underline{\bf u}_h^{m+1},\theta)\right) \geq2C_{coe}\Delta t \left\|B(\underline{\bf u}_h^{m+1},\theta)\right\|_{\bf U}^2. \end{matrix}$

(3.11)

由无散度特性可知, 左边第三项等于 0. 最后, 根据 Young 不等式和 Cauchy Schwarz 不等式, 有

$\begin{aligned} & 2 \Delta t\left\langle(1-\theta) \mathbf{F}^{m+1}+\theta \mathbf{F}^{m}, B\left(\underline{\mathbf{u}}_{h}^{m+1}, \theta\right)\right\rangle \\ \leq & \frac{2 \theta^{2} \Delta t}{C_{\text {coe }}}\left\|\mathbf{F}^{m}\right\|_{\mathbf{U}^{\prime}}^{2}+\frac{2(1-\theta)^{2} \Delta t}{C_{\text {coe }}}\left\|\mathbf{F}^{m+1}\right\|_{\mathbf{U}^{\prime}}^{2}+C_{c o e} \Delta t\left\|B\left(\underline{\mathbf{u}}_{h}^{m+1}, \theta\right)\right\|_{\mathbf{U}^{2}}^{2}. \end{aligned}$

(3.12)

结合 (3.10)-(3.12) 式, 并将 (3.9) 式从 $m=1$ 直到 $m=N-1$ 求和, 整理得

$\begin{eqnarray*} &&(2\theta^2-5\theta+3)\|\underline{\bf u}_h^{N}\|^2_0 +(1-2\theta)(1-\theta)\|\underline{\bf u}_h^{N-1}\|^2_0\\ &&-(1-2\theta)(3-2\theta)\|\underline{\bf u}_h^{N}\|_0\|\underline{\bf u}_h^{N-1}\|_0 +C_{coe}\Delta t\sum_{m=1}^{N-1} \left\|B(\underline{\bf u}_h^{m+1},\theta)\right\|_{\bf U}^2\\ &\leq&\frac{2\theta^2\Delta t}{C_{coe}}\sum_{m=1}^{N-1}\|{\bf F}^{m}\|_{{\bf U}'}^2 +\frac{2(1-\theta)^2\Delta t}{C_{coe}}\sum_{m=1}^{N-1}\|{\bf F}^{m+1}\|_{{\bf U}'}^2\\ & &+(2\theta^2-5\theta+3)\|\underline{\bf u}_h^{1}\|^2_0 +(1-2\theta)(1-\theta)\|\underline{\bf u}_h^{0}\|^2_0 -(1-2\theta)(3-2\theta)\|\underline{\bf u}_h^{1}\|_0\|\underline{\bf u}_h^{0}\|_0. \end{eqnarray*}$

由于

$-(1-2\theta)(3-2\theta)\|\underline{\bf u}_h^{N}\|_0\|\underline{\bf u}_h^{N-1}\|_0 \geq -\frac{(1-2\theta)(3-2\theta)^2}{4(1-\theta)}\|\underline{\bf u}_h^{N}\|_0^2 -(1-2\theta)(1-\theta)\|\underline{\bf u}_h^{N-1}\|^2_0,$

因此

$\begin{eqnarray*} &&\frac{3-2\theta}{4(1-\theta)}\|\underline{\bf u}_h^{N}\|^2_0 +C_{coe}\Delta t\sum_{m=1}^{N-1} \left\|B(\underline{\bf u}_h^{m+1},\theta)\right\|_{\bf U}^2\\ &\leq&\frac{2\theta^2\Delta t}{C_{coe}}\sum_{m=1}^{N-1}\|{\bf F}^{m}\|_{{\bf U}'}^2 +\frac{2(1-\theta)^2\Delta t}{C_{coe}}\sum_{m=1}^{N-1}\|{\bf F}^{m+1}\|_{{\bf U}'}^2\\ & &+(2\theta^2-5\theta+3)\|\underline{\bf u}_h^{1}\|^2_0 +(1-2\theta)(1-\theta)\|\underline{\bf u}_h^{0}\|^2_0 -(1-2\theta)(3-2\theta)\|\underline{\bf u}_h^{1}\|_0\|\underline{\bf u}_h^{0}\|_0, \end{eqnarray*}$

从而得到耦合算法的稳定性结论.证毕.

3.2 解耦算法及其稳定性

解耦的线性多步法加 time filter 算法表述如下.

$\blacktriangledown$ 线性多步法 (一阶收敛)

给定 $({\bf u}_{fh}^0,p_{fh}^0)$ 和 $({\bf u}_{fh}^1,p_{fh}^1)$ , 求 $(\hat{\bf u}_{fh}^{m+1},\hat{p}_{fh}^{m+1})\in({\bf H}_{fh},Q_{fh})$ , $m=1,2,\cdots,N-1$ , 使得 $\forall\ {\bf v}_{fh} \in{\bf H} _{fh}$ , $q_{fh}\in Q_{fh}$ ,有

$\begin{eqnarray*} \label{DS} &&\bigg(\frac{\hat{\bf u}_{fh}^{m+1}-{\bf u}_{fh}^m}{\Delta t},{\bf v}_{fh}\bigg)_{\Omega_f} +a_{\Omega_f}\left((1-\theta)\hat{\bf u}_{fh}^{m+1}+\theta{\bf u}_{fh}^{m},{\bf v}_{fh}\right) +b\left({\bf v}_{fh},(1-\theta)\hat{p}_{fh}^{m+1}+\theta p_{fh}^m\right)\nonumber\\ &=&\left((1-\theta){\bf g}_{f}^{m+1}+\theta{\bf g}_{f}^{m},{\bf v}_{fh}\right)_{\Omega_f} -c_{\Gamma}\left({\bf v}_{fh},(2-\theta)\phi_{ph}^m-(1-\theta)\phi_{ph}^{m-1}\right),\\ &&b\left((1-\theta)\hat{\bf u}_{fh}^{m+1}+\theta{\bf u}_{fh}^{m},q_{fh}\right)=0.\nonumber \end{eqnarray*}$

(3.13)

给定 $\phi_{ph}^0$ 和 $\phi_{ph}^1$ , 求 $\hat{\phi}_{ph}^{m+1}\in{\bf H}_{ph}$ , $m=1,2,\cdots,N-1$ , 使得 $\forall$ $\psi_{ph} \in{\bf H}_{ph}$ ,有

$\begin{matrix} \label{DD} &&g\bigg(\frac{\hat{\phi}_{ph}^{m+1}-\phi_{ph}^m}{\Delta t},\psi_{ph}\bigg)_{{\Omega}_p} +a_{\Omega_p}\left((1-\theta)\hat{\phi}_{ph}^{m+1}+\theta\phi_{ph}^{m},\psi_{ph}\right)\\ &=&g\left((1-\theta){\bf g}_{p}^{m+1}+\theta {\bf g}_{p}^{m},\psi_{ph}\right)_{\Omega_p} +c_{\Gamma}\left((2-\theta){\bf u}_{fh}^m-(1-\theta){\bf u}_{fh}^{m-1},\psi_{ph}\right). \end{matrix}$

(3.14)

$\blacktriangledown$ Time Filter 算法 (二阶收敛)

通过 time filter 算法更新线性多步法的解 $(\hat{\bf u}_{fh}^{m+1},\hat{p}_{fh}^{m+1},\hat{\phi}_{ph}^{m+1})$ ,

$\begin{matrix} \label{time filter} &&{\bf u}_{fh}^{m+1}=\hat{\bf u}_{fh}^{m+1}-\frac{1-2\theta}{3-2\theta}(\hat{\bf u}_{fh}^{m+1}-2{\bf u}_{fh}^{m}+{\bf u}_{fh}^{m-1}),\\ &&p_{fh}^{m+1}=\hat{p}_{fh}^{m+1}-\frac{1-2\theta}{3-2\theta}(\hat{p}_{fh}^{m+1}-2p_{fh}^{m}+p_{fh}^{m-1}),\\ &&\phi_{ph}^{m+1}=\hat{\phi}_{ph}^{m+1}-\frac{1-2\theta}{3-2\theta}(\hat{\phi}_{ph}^{m+1}-2\phi_{ph}^m+\phi_{ph}^{m-1}). \end{matrix}$

(3.15)

${\bf注3.2}$ 交界面项利用二阶外推方法近似 $\hat{\bf u}_{fh}^{m+1}$ 和 $\hat{\phi}_{ph}^{m+1}$ , 即 $\hat{\bf u}_{fh}^{m+1}\approx 2{\bf u}_{fh}^{m}-{\bf u}_{fh}^{m-1}$ , $\hat{\phi}_{ph}^{m+1}\approx 2\phi_{ph}^{m}-\phi_{ph}^{m-1}$ . 类似地, 无论压力 $\hat{p}_{fh}^{m+1}$ 是否经 time filter 更新, 最终的结果几乎一致.

下面给出解耦的线性多步法加 time filter 算法的稳定性分析.

${\bf定理3.2}$ (解耦算法的稳定性) 设 ${\bf u}_{fh}^{m+1}$ , $\phi_{ph}^{m+1}$ 是线性多步法加 time filter 算法的解. 对于 $N\geq 2$ , 有

其中 $C(T)=\exp\Big(\sum\limits_{m=1}^{N-1}\max\left\{\frac{8(1-\theta)\Delta t}{(3-2\theta)\hat{C}_{coe}},\frac{8(1-\theta)\Delta t}{(3-2\theta)\check{C}_{coe}} \right\}\Big)$ .

${\bf证}$ 由 (3.15) 式可得

$\begin{matrix} &&\hat{\bf u}_{fh}^{m+1}=\frac{3-2\theta}{2}{\bf u}_{fh}^{m+1}-(1-2\theta){\bf u}_{fh}^{m}+\frac{1-2\theta}{2}{\bf u}_{fh}^{m-1},\nonumber\\ &&\hat{p}_{fh}^{m+1}=\frac{3-2\theta}{2}{p}_{fh}^{m+1}-(1-2\theta){p}_{fh}^{m}+\frac{1-2\theta}{2}{p}_{fh}^{m-1},\nonumber\\ &&\hat{\phi}_{ph}^{m+1}=\frac{3-2\theta}{2}\phi_{ph}^{m+1}-(1-2\theta)\phi_{ph}^{m}+\frac{1-2\theta}{2}\phi_{ph}^{m-1},\nonumber \end{matrix}$

将上述三式分别代入 (3.13) 和 (3.14) 式后相加, $\forall\ {\bf v}_{fh}\in{\bf H}_{fh}, \psi_{ph}\in{\bf H}_{ph}, q_{fh}\in Q_{fh}$ ,有

$\begin{eqnarray*} \label{TT} &&\frac{1}{\Delta t}\bigg(A({\bf u}_{fh}^{m+1},\theta),{\bf v}_{fh}\bigg)_{\Omega_f} +a_{\Omega_f}\left(B({\bf u}_{fh}^{m+1},\theta),{\bf v}_{fh}\right) +b\left({\bf v}_{fh},B(p_{fh}^{m+1},\theta)\right)\nonumber\\ &&+g\frac{1}{\Delta t}\bigg(A(\phi_{ph}^{m+1},\theta),\psi_{ph}\bigg)_{\Omega_p} +a_{\Omega_p}\left(B(\phi_{ph}^{m+1},\theta),\psi_{ph}\right)\nonumber\\ &=&\left((1-\theta){\bf g}_{f}^{m+1}+\theta{\bf g}_{f}^{m},{\bf v}_{fh}\right)_{\Omega_f} +g\left((1-\theta){\bf g}_{p}^{m+1}+\theta {\bf g}_{p}^{m},\psi_{ph}\right)_{\Omega_p}\\ &&-c_{\Gamma}\left({\bf v}_{fh},(2-\theta)\phi_{ph}^m-(1-\theta)\phi_{ph}^{m-1}\right) +c_{\Gamma}\left((2-\theta){\bf u}_{fh}^m-(1-\theta){\bf u}_{fh}^{m-1},\psi_{ph}\right),\nonumber\\ &&b\left(B({\bf u}_{fh}^{m+1},\theta), q_{fh}\right)=0.\nonumber \end{eqnarray*}$

(3.16)

假设 ${\bf v}_{fh}=2\Delta t B({\bf u}_{fh}^{m+1},\theta)$ , $\psi_{ph}=2\Delta t B(\phi_{ph}^{m+1},\theta)$ , $q_{fh}=2\Delta t B(p_{fh}^{m+1},\theta)$ . 类似定理 3.1 的证明, 有以下不等式成立

$\begin{aligned} & 2\left(A\left(\mathbf{u}_{f h}^{m+1}, \theta\right), B\left(\mathbf{u}_{f h}^{m+1}, \theta\right)\right)_{\Omega_f} \\ \geq & \left(2 \theta^2-5 \theta+3\right)\left\|\mathbf{u}_{f h}^{m+1}\right\|_f^2-2(1-\theta)\left\|\mathbf{u}_{f h}^m\right\|_f^2-(1-2 \theta)(1-\theta)\left\|\underline{\mathbf{u}}_h^{m-1}\right\|_f^2 \\ & -(1-2 \theta)(3-2 \theta)\left(\left\|\mathbf{u}_{f h}^{m+1}\right\|_f\left\|\mathbf{u}_{f h}^m\right\|_f-\left\|\mathbf{u}_{f h}^m\right\|_f\left\|\mathbf{u}_{f h}^{m-1}\right\|_f\right),\end{aligned}$

(3.17)

$\begin{aligned} & 2g\big(A(\phi_{ph}^{m+1},\theta),B(\phi_{ph}^{m+1},\theta)\big)_{\Omega_{p}}\nonumber\\ \geq & g\big[(2\theta^2-5\theta+3)\|\phi_{ph}^{m+1}\|^2_p -2(1-\theta)\|\phi_{ph}^{m}\|^2_p -(1-2\theta)(1-\theta)\|\phi_{ph}^{m-1}\|^2_p\nonumber\\ &-(1-2\theta)(3-2\theta)\left(\|\phi_{ph}^{m+1}\|_p\|\phi_{ph}^{m}\|_p -\|\phi_{ph}^{m}\|_p\|\phi_{ph}^{m-1}\|_p\right)\big],\end{aligned}$

(3.18)

$\begin{aligned} & 2\Delta t a_{\Omega_f} \left(B({\bf u}_{fh}^{m+1},\theta),B({\bf u}_{fh}^{m+1},\theta)\right) \geq 2\hat{C}_{coe}\Delta t \left\|B({\bf u}_{fh}^{m+1},\theta)\right\|_{H_f}^2,\end{aligned}$

(3.19)

$\begin{aligned} & 2\Delta t a_{\Omega_p} \left(B(\phi_{ph}^{m+1},\theta),B(\phi_{ph}^{m+1},\theta)\right) \geq2g\check{C}_{coe}\Delta t \left\|B(\phi_{ph}^{m+1},\theta)\right\|_{H_p}^2,\end{aligned}$

(3.20)

$\begin{aligned} & 2 \Delta t\left((1-\theta) \mathbf{g}_f^{m+1}+\theta \mathbf{g}_f^m, B\left(\mathbf{u}_{f h}^{m+1}, \theta\right)\right)_{\Omega_f} \\ \leq & \frac{2 \theta^2 \Delta t}{\hat{C}_{\text {coe }}}\left\|\mathbf{g}_f^m\right\|_{\mathbf{H}_f^{\prime}}^2+\frac{2(1-\theta)^2 \Delta t}{\hat{C}_{\text {coe }}}\left\|\mathbf{g}_f^{m+1}\right\|_{\mathbf{H}_f^{\prime}}^2+\frac{\hat{C}_{c o e} \Delta t}{2}\left\|B\left(\mathbf{u}_{f h}^{m+1}, \theta\right)\right\|_{\mathbf{H}_f}^2,\end{aligned}$

(3.21)

$\begin{aligned} & 2g\Delta t\left((1-\theta){\bf g}_{p}^{m+1}+\theta {\bf g}_{p}^{m}, B(\phi_{ph}^{m+1},\theta)\right)_{\Omega_{p}}\\ \leq & \frac{2 g \theta^2 \Delta t}{\check{C}_{\text {coe }}}\left\|{\bf g}_p^m\right\|_{\mathbf{H}_p^{\prime}}^2+\frac{2 g(1-\theta)^2 \Delta t}{\check{C}_{\text {coe }}}\left\|{\bf g}_p^{m+1}\right\|_{\mathbf{H}_p^{\prime}}^2+\frac{g \check{C}_{c o e} \Delta t}{2}\left\|B\left(\phi_{p h}^{m+1}, \theta\right)\right\|_{\mathbf{H}_p}^2.\end{aligned}$

(3.22)

这里主要分析交界面项. 借助引理 3.2, 并代入 $\varepsilon_1=\frac{1}{\hat{C}_{coe}}$ , $\varepsilon_2=\frac{g}{\check{C}_{coe}}$ , 有

$\begin{eqnarray*}\label{R12} &&-2\Delta tc_{\Gamma} \left(B({\bf u}_{fh}^{m+1},\theta), (2-\theta)\phi_{ph}^m-(1-\theta)\phi_{ph}^{m-1}\right)\nonumber\\ &&+2\Delta tc_{\Gamma} \left((2-\theta){\bf u}_{fh}^m-(1-\theta){\bf u}_{fh}^{m-1}, B(\phi_{ph}^{m+1},\theta)\right)\nonumber\\ &\leq &\frac{\hat{C}_{coe}\Delta t}{2} \left\|B({\bf u}_{fh}^{m+1},\theta)\right\|_{{\bf H}_f}^2 +\frac{2C_1h^{-1}\Delta t}{\hat{C}_{coe}} \|(2-\theta)\phi_{ph}^m-(1-\theta)\phi_{ph}^{m-1}\|_p^2\\ &&+\frac{g\check{C}_{coe}\Delta t}{2} \left\| B(\phi_{ph}^{m+1},\theta)\right\|_{{\bf H}_p}^2 +\frac{2gC_2h^{-1}\Delta t}{\check{C}_{coe}} \|(2-\theta){\bf u}_{fh}^m-(1-\theta){\bf u}_{fh}^{m-1}\|_f^2\nonumber\\ &\leq &\frac{\hat{C}_{coe}\Delta t}{2} \left\|B({\bf u}_{fh}^{m+1},\theta)\right\|_{{\bf H}_f}^2 +\frac{g\check{C}_{coe}\Delta t}{2} \left\| B(\phi_{ph}^{m+1},\theta)\right\|_{{\bf H}_p}^2\nonumber\\ &&+\frac{2g\Delta t}{\hat{C}_{coe}} \|(2-\theta)\phi_{ph}^m-(1-\theta)\phi_{ph}^{m-1}\|_p^2 +\frac{2\Delta t}{\check{C}_{coe}} \|(2-\theta){\bf u}_{fh}^m-(1-\theta){\bf u}_{fh}^{m-1}\|_f^2, \end{eqnarray*}$

(3.23)

其中, 最后一个不等式是在选择合适的常量 $C_1$ 和 $C_2$ 下得到的.

结合 (3.17)-(3.23) 式, 并将 (3.16) 式从 $m=1$ 直到 $m=N-1$ 求和, 整理可得

$\begin{eqnarray*} &&(2\theta^2-5\theta+3)\|{\bf u}_{fh}^{N}\|^2_f +(1-2\theta)(1-\theta)\|{\bf u}_{fh}^{N-1}\|^2_f\\ &&+g(2\theta^2-5\theta+3)\|\phi_{ph}^{N}\|^2_p +g(1-2\theta)(1-\theta)\|\phi_{ph}^{N-1}\|^2_p\\ &&-(1-2\theta)(3-2\theta)\|{\bf u}_{fh}^{N}\|_f\|{\bf u}_{fh} ^{N-1}\|_f -g(1-2\theta)(3-2\theta){2}\|\phi_{ph}^{N}\|_p\|\phi_{ph}^{N-1}\|_p\\ &&+\hat{C}_{coe}\Delta t\sum_{m=1}^{N-1} \left\|B({\bf u}_{fh}^{m+1},\theta)\right\|_{{\bf H}_f}^2 +g\check{C}_{coe}\Delta t\sum_{m=1}^{N-1} \left\|B(\phi_{ph}^{m+1},\theta)\right\|_{{\bf H}_p}^2\\ &\leq &\frac{2\theta^2\Delta t}{\hat{C}_{coe}}\sum_{m=1}^{N-1}\|{\bf g}_f^m\|_{{\bf H}_f'}^2 +\frac{2(1-\theta)^2\Delta t}{\hat{C}_{coe}}\sum_{m=1}^{N-1}\|{\bf g}_f^{m+1}\|_{{\bf H}_f'}^2\\ &&+\frac{2g\theta^2\Delta t}{\check{C}_{coe}}\sum_{m=1}^{N-1}\|{\bf g}_p^m\|_{{\bf H}_p'}^2 +\frac{2g(1-\theta)^2\Delta t}{\check{C}_{coe}}\sum_{m=1}^{N-1}\|{\bf g}_p^{m+1}\|_{{\bf H}_p'}^2\\ &&+\frac{2g\Delta t}{\hat{C}_{coe}} \|(2-\theta)\phi_{ph}^m-(1-\theta)\phi_{ph}^{m-1}\|_p^2 +\frac{2\Delta t}{\check{C}_{coe}} \|(2-\theta){\bf u}_{fh}^m-(1-\theta){\bf u}_{fh}^{m-1}\|_f^2\\ &&+(2\theta^2-5\theta+3)\|{\bf u}_{fh}^1\|_f^2 +(1-2\theta)(1-\theta)\|{\bf u}_{fh}^0\|_f^2\\ &&+g(2\theta^2-5\theta+3)\|\phi_{ph}^1\|_p^2 +g(1-2\theta)(1-\theta)\|\phi_{ph}^0\|_p^2\\ &&-(1-2\theta)(3-2\theta)\|{\bf u}_{fh}^{1}\|_f\|{\bf u}_{fh}^{0}\|_f -g(1-2\theta)(3-2\theta)\|\phi_{ph}^{1}\|_p\|\phi_{ph}^{0}\|_p. \end{eqnarray*}$

(3.24)

由于

$\begin{eqnarray*} &&-(1-2\theta)(3-2\theta)\|{\bf u}_{fh}^{N}\|_f\|{\bf u}_{fh}^{N-1}\|_f\\ &\geq &-\frac{(1-2\theta)(3-2\theta)^2}{4(1-\theta)}\|{\bf u}_{fh}^{N}\|_f^2 -(1-2\theta)(1-\theta)\|{\bf u}_{fh}^{N-1}\|^2_f, \end{eqnarray*}$

以及

$\begin{eqnarray*} &&-g(1-2\theta)(3-2\theta)\|\phi_{ph}^{N}\|_p\|\phi_{ph}^{N-1}\|_p\\ &\geq &-g\frac{(1-2\theta)(3-2\theta)^2}{4(1-\theta)}\|\phi_{ph}^{N}\|_p^2 -g(1-2\theta)(1-\theta)\|\phi_{ph}^{N-1}\|^2_p, \end{eqnarray*}$

因此

$\begin{eqnarray*} &&\frac{3-2\theta}{4(1-\theta)}\|{\bf u}_{fh}^{N}\|^2_f +\hat{C}_{coe}\Delta t\sum_{m=1}^{N-1} \left\|B({\bf u}_{fh}^{m+1},\theta)\right\|_{{\bf H}_f}^2\\ &&+\frac{g(3-2\theta)}{4(1-\theta)}\|\phi_{ph}^{N}\|^2_p +g\check{C}_{coe}\Delta t\sum_{m=1}^{N-1} \left\|B(\phi_{ph}^{m+1},\theta)\right\|_{{\bf H}_p}^2\\ &\leq &\frac{2\theta^2\Delta t}{\hat{C}_{coe}}\sum_{m=1}^{N-1}\|{\bf g}_f^m\|_{{\bf H}_f'}^2 +\frac{2(1-\theta)^2\Delta t}{\hat{C}_{coe}}\sum_{m=1}^{N-1}\|{\bf g}_f^{m+1}\|_{{\bf H}_f'}^2\\ &&+\frac{2g\theta^2\Delta t}{\check{C}_{coe}}\sum_{m=1}^{N-1}\|{\bf g}_p^m\|_{{\bf H}_p'}^2 +\frac{2g(1-\theta)^2\Delta t}{\check{C}_{coe}}\sum_{m=1}^{N-1}\|{\bf g}_p^{m+1}\|_{{\bf H}_p'}^2\\ &&+\frac{8(1-\theta)\Delta t}{(3-2\theta)\hat{C}_{coe}}\sum_{m=1}^{N-1} \frac{g(3-2\theta)}{4(1-\theta)}\|\phi_{ph}^m\|_p^2 +\frac{8(1-\theta)\Delta t}{(3-2\theta)\check{C}_{coe}}\sum_{m=1}^{N-1} \frac{(3-2\theta)}{4(1-\theta)}\Vert {\bf u}_{fh}^m \Vert_f^2\\ &&+(2\theta^2-5\theta+3)\|{\bf u}_{fh}^1\|_f^2 +(1-2\theta)(1-\theta)\|{\bf u}_{fh}^0\|_f^2\nonumber\\ &&+g(2\theta^2-5\theta+3)\|\phi_{ph}^1\|_p^2 +g(1-2\theta)(1-\theta)\|\phi_{ph}^0\|_p^2\nonumber\\ &&-(1-2\theta)(3-2\theta)\|{\bf u}_{fh}^{1}\|_f\|{\bf u}_{fh}^{0}\|_f -g(1-2\theta)(3-2\theta)\|\phi_{ph}^{1}\|_p\|\phi_{ph}^{0}\|_p. \end{eqnarray*}$

结合离散的 Gronwall 引理可得解耦算法的稳定性结论. 证毕.

4 误差估计

本节将证明耦合和解耦算法的误差估计. 记算法的精确解为 $(\underline{\bf u}^{m+1},p_f^{m+1})=$ $(\underline{\bf u}(t_{m+1}),$ $p_f(t_{m+1}))$ , 其中 $\underline{\bf u}^{m+1}=({\bf u}_f^{m+1},\phi_f^{m+1})$ , $\underline{\bf u}(t_{m+1})=({\bf u}_f(t_{m+1}),\phi_f(t_{m+1}))$ , 同时定义误差函数

$\begin{eqnarray*} &&e_{\underline{\bf u}}^{m}=\underline{\bf u}_h^{m}-\underline{\bf u}^{m}=\underline{\bf u}_h^{m}-P_h^{\underline{\bf u}}\underline{\bf u}^{m}+P_h^{\underline{\bf u}}\underline{\bf u}^{m}-\underline{\bf u}^{m}=\eta_{\underline{\bf u}}^m+\xi_{\underline{\bf u}}^m,\\ &&e_{p}^{m}=p_{fh}^{m}-p_{f}^{m}=p_{fh}^{m}-P_h^{p}p_{f}^{m}+P_h^{p}p_{f}^{m}-p_{f}^{m}=\eta_{p}^m+\xi_{p}^m,\\ &&e_{{\bf u}_f}^{m}={\bf u}_{fh}^{m}-{\bf u}_f^{m}={\bf u}_{fh}^{m}-P_h^{{\bf u}_f}{\bf u}_f^{m}+P_h^{{\bf u}_f}{\bf u}_f^{m}-{\bf u}_f^{m}=\eta_{{\bf u}_f}^m+\xi_{{\bf u}_f}^m,\\ &&e_{\phi_p}^{m}=\phi_{ph}^{m}-\phi_{p}^{m}=\phi_{ph}^{m}-P_h^{\phi_p}\phi_{p}^{m}+P_h^{\phi_p}\phi_{p}^{m}-\phi_{p}^{m}=\eta_{\phi_{p}}^m+\xi_{\phi_{p}}^m. \end{eqnarray*}$

显然地, 下述关系式成立

$\begin{matrix} \label{theta} &&\|\xi_{\underline{\bf u}}^m\|_0\leq Ch^2\|\underline{\bf u}(t)\|_{H^2},\quad \|\xi_{\underline{\bf u}}^m\|_{\bf U}\leq Ch\|\underline{\bf u}(t)\|_{H^2},\quad \|\xi_{p}^m\|_{L^2}\leq Ch\|p_f(t)\|_{H^1},\nonumber\\ &&\|\xi_{{\bf u}_f}^m\|_{f}\leq Ch^2\|{\bf u}_f(t)\|_{H^2},\quad \|\xi_{{\bf u}_f}^m\|_{{\bf H}_f}\leq Ch\|{\bf u}_f(t)\|_{H^2},\\ &&\|\xi_{\phi_p}^m\|_{p}\leq Ch^2\|\phi_p(t)\|_{H^2},\quad \|\xi_{\phi_p}^m\|_{{\bf H}_p}\leq Ch\|\phi_p(t)\|_{H^2}.\nonumber \end{matrix}$

(4.1)

需注意 $\eta_{\underline{\bf u}}^0=0$ , $\eta_{p}^0=0$ , $\eta_{{\bf u}_f}^0=0$ , $\eta_{\phi_p}^0=0$ .

假设所求解满足下述正则性条件

$\begin{matrix} \label{regularity} \begin{array}{ll} {\bf u}_f\in L^{\infty}(0,T;{\bf H}^2), {\bf u}_{f,t}\in {\bf L}^{2}(0,T;{\bf H}^1)\cap L^{\infty}(0,T;{\bf L}^2),\\ {\bf u}_{f,tt}\in {\bf L}^{2}(0,T;{\bf L}^2), {\bf u}_{f,ttt}\in L^{2}(0,T;{\bf H}'),\\ \phi_p\in L^{\infty}(0,T;{\bf H}^2), \phi_{p,t}\in {\bf L}^{2}(0,T;{\bf H}^1)\cap L^{\infty}(0,T;{\bf L}^2),\\ \phi_{p,tt}\in L^{2}(0,T;{\bf L}^2), \phi_{p,ttt}\in {\bf L}^{2}(0,T;{\bf H}'). \end{array} \end{matrix}$

(4.2)

外力项 ${\bf g}_f$ 和 ${\bf g}_p$ 满足

$\begin{matrix} \label{regularity1} \begin{array}{ll} {\bf g}_{f,t}\in {\bf L}^{2}(0,T;{\bf L}^2),\ {\bf g}_{f,tt}\in {\bf L}^{2}(0,T;{\bf H}_f'),\\ {\bf g}_{p,t}\in {\bf L}^{2}(0,T;{\bf L}^2),\ {\bf g}_{p,tt}\in L^{2}(0,T;{\bf H}_p'). \end{array} \end{matrix}$

(4.3)

4.1 耦合算法的误差估计

${\bf定理4.1}$ (耦合算法的二阶收敛性) 在 (4.2)和(4.3) 式的假设下, 对于 $N\geq 2$ 有以下估计

$\begin{eqnarray*} \frac{3-2\theta}{4(1-\theta)}\|e_{\underline{\bf u}}^{N}\|_0^2+C_{coe}\Delta t\sum_{m=1}^{N-1}\left\|B(e_{\underline{\bf u}}^{m+1},\theta)\right\|_{\bf U}^2\leq C (\Delta t^4+h^4). \end{eqnarray*}$

${\bf证}$ 在 $t_{m+1}$ , $t_{m}$ 和 $t_{m-1}$ 时刻分别对 (2.11) 式乘 $\frac{(1-\theta)(3-2\theta)}{2}$ , $(4\theta-1-2\theta^2)$ , $\frac{(1-\theta)(1-2\theta)}{2}$ 得到三个对应时刻的等式. 从 (3.9) 式中减去三者之和, 结合误差函数的定义和投影算子的性质 (3.2) 式可得, $\forall\ \underline{\bf v}_h\in{\bf u}_h$ , $\ q_{fh}\in Q_{fh}$ ,有

$\begin{aligned} & \frac{1}{\Delta t}\left(A\left(\eta_{\underline{\mathbf{u}}}^{m+1}, \theta\right), \underline{\mathbf{v}}_{h}\right)+a\left(B\left(\eta_{\underline{\mathbf{u}}}^{m+1}, \theta\right), \underline{\mathbf{v}}_{h}\right)+b\left(\underline{\mathbf{v}}_{h}, B\left(\eta_{p}^{m+1}, \theta\right)\right) \\ = & -\left(\frac{1}{\Delta t} A\left(\underline{\mathbf{u}}^{m+1}, \theta\right)-B\left(\underline{\mathbf{u}}_{t}^{m+1}, \theta\right), \underline{\mathbf{v}}_{h}\right)-\left(\frac{1}{\Delta t} A\left(\xi_{\underline{\mathbf{u}}}^{m+1}, \theta\right), \underline{\mathbf{v}}_{h}\right)+\left\langle F\left(\mathbf{F}^{m+1}, \theta\right), \underline{\mathbf{v}}_{h}\right\rangle, \\ & b\left(B\left(\eta_{\underline{\mathbf{u}}}^{m+1}, \theta\right), q_{f h}\right)=0. \end{aligned}$

(4.4)

假设 $\underline{\bf v}_h=2\Delta t B(\eta_{\underline{\bf u}}^{m+1},\theta)$ , $q_{fh}=2\Delta t B(\eta_{p}^{m+1},\theta)$ . 类似定理 3.1 的证明, 对 (4.4) 式的每一项进行分析.

首先, 借助引理 3.1, 有

$\begin{eqnarray*} \label{errorl1} &&2\left(A(\eta_{\underline{\bf u}}^{m+1},\theta),B(\eta_{\underline{\bf u}}^{m+1},\theta)\right)\\ &\geq &(2\theta^2-5\theta+3)\|\eta_{\underline{\bf u}}^{m+1}\|^2_0 -2(1-\theta)\|\eta_{\underline{\bf u}}^{m}\|^2_0 -(1-2\theta)(1-\theta)\|\eta_{\underline{\bf u}}^{m-1}\|^2_0\nonumber\\ &&-(1-2\theta)(3-2\theta)(\|\eta_{\underline{\bf u}}^{m+1}\|_0\|\eta_{\underline{\bf u}}^{m}\|_0 -\|\eta_{\underline{\bf u}}^{m}\|_0\|\eta_{\underline{\bf u}}^{m-1}\|_0). \end{eqnarray*}$

(4.5)

利用双线性形式 $a(\cdot,\cdot)$ 的强制性可得

$2\Delta t a\left(B(\eta_{\underline{\bf u}}^{m+1},\theta),B(\eta_{\underline{\bf u}}^{m+1},\theta)\right) \geq 2C_{coe}\Delta t \left\|B(\eta_{\underline{\bf u}}^{m+1},\theta)\right\|_{\bf U}^2.\nonumber$

由无散度特性可知, 左边第三项的结果为 0.

其次, 利用积分型余项的泰勒展开式,有

$\begin{eqnarray*} \label{taylor} &&\underline{\bf u}^{m}=\underline{\bf u}^{m+1}-\Delta t\underline{\bf u}^{m+1}_t+\frac{\Delta t^2}{2}\underline{\bf u}^{m+1}_{tt}+\frac{1}{2}\int_{t^{m+1}}^{t^{m}}(t^{m}-t)^2\underline{\bf u}_{ttt}{\rm d}t,\\ &&\underline{\bf u}^{m-1}=\underline{\bf u}^{m+1}-2\Delta t\underline{\bf u}^{m+1}_t+2\Delta t^2\underline{\bf u}^{m+1}_{tt}+\frac{1}{2}\int_{t^{m+1}}^{t^{m-1}}(t^{m-1}-t)^2\underline{\bf u}_{ttt}{\rm d}t,\\ &&\underline{\bf u}^{m}_t=\underline{\bf u}^{m+1}_t-\Delta t\underline{\bf u}^{m+1}_{tt}+\int_{t^{m+1}}^{t^{m}}(t^{m}-t)\underline{\bf u}_{ttt}{\rm d}t,\\ &&\underline{\bf u}^{m-1}_t=\underline{\bf u}^{m+1}_t-2\Delta t\underline{\bf u}^{m+1}_{tt}+\int_{t^{m+1}}^{t^{m-1}}(t^{m-1}-t)\underline{\bf u}_{ttt}{\rm d}t, \end{eqnarray*}$

代入并整理得

$\begin{eqnarray*} &&\frac{1}{\Delta t}A(\underline{\bf u}^{m+1},\theta)-B(\underline{\bf u}_{t}^{m+1},\theta)\\ &=&\frac{1}{\Delta t} \bigg[(1-\theta)\int_{t^{m}}^{t^{m+1}}(t^{m}-t)^2\underline{\bf u}_{ttt}{\rm d}t -\frac{1-2\theta}{4}\int_{t^{m-1}}^{t^{m+1}}(t^{m-1}-t)^2\underline{\bf u}_{ttt}{\rm d}t\bigg]\\ &&-(4\theta-1-2\theta^2)\int_{t^{m}}^{t^{m+1}}(t^{m}-t)\underline{\bf u}_{ttt}{\rm d}t -\frac{(1-\theta)(1-2\theta)}{2}\int_{t^{m-1}}^{t^{m+1}}(t^{m-1}-t)\underline{\bf u}_{ttt}{\rm d}t. \end{eqnarray*}$

再结合 Cauchy-Schwarz 不等式,有

$\begin{eqnarray*} &&\bigg(\int_{t^{m}}^{t^{m+1}}(t^{m}-t)^2\underline{\bf u}_{ttt}{\rm d}t\bigg)^2\leq \frac{\Delta t^5}{5}\int_{t^{m}}^{t^{m+1}}\underline{\bf u}_{ttt}^2{\rm d}t,\\ &&\bigg(\int_{t^{m-1}}^{t^{m+1}}(t^{m-1}-t)^2\underline{\bf u}_{ttt}{\rm d}t\bigg)^2 \leq \frac{32\Delta t^5}{5}\int_{t^{m-1}}^{t^{m+1}}\underline{\bf u}_{ttt}^2{\rm d}t,\\ &&\bigg(\int_{t^{m}}^{t^{m+1}}(t^{m}-t)\underline{\bf u}_{ttt}{\rm d}t\bigg)^2\leq \frac{\Delta t^3}{3}\int_{t^{m}}^{t^{m+1}}\underline{\bf u}_{ttt}^2{\rm d}t,\\ &&\bigg(\int_{t^{m-1}}^{t^{m+1}}(t^{m-1}-t)\underline{\bf u}_{ttt}{\rm d}t\bigg)^2 \leq \frac{8\Delta t^3}{3}\int_{t^{m-1}}^{t^{m+1}}\underline{\bf u}_{ttt}^2{\rm d}t, \end{eqnarray*}$

可以得到

$\begin{eqnarray*} &&2\Delta t\left( \frac{1}{\Delta t}A(\underline{\bf u}^{m+1},\theta)-B(\underline{\bf u}_{t}^{m+1},\theta), B(\eta_{\underline{\bf u}}^{m+1},\theta)\right)\nonumber\\ &\leq& \frac{3\Delta t}{C_{coe}} \left\|\frac{1}{\Delta t}A(\underline{\bf u}^{m+1},\theta)-B(\underline{\bf u}_{t}^{m+1},\theta)\right\|_{\bf U}^2 +\frac{C_{coe}\Delta t}{3} \left\|B(\eta_{\underline{\bf u}}^{m+1},\theta)\right\|_{\bf U}^2\\ &\leq & \frac{ (60\theta^4-200\theta^3+257\theta^2-130\theta+24)\Delta t^4}{5C_{coe}} \int_{t^{m-1}}^{t^{m+1}}\|\underline{\bf u}_{ttt}\|^2_{\bf U'}{\rm d}t +\frac{C_{coe}\Delta t}{3} \left\|B(\eta_{\underline{\bf u}}^{m+1},\theta)\right\|_{\bf U}^2.\nonumber \end{eqnarray*}$

(4.6)

类似地, 借助积分型余项的泰勒展开式,有

$\begin{eqnarray*} \underline{\bf u}^{m}=\underline{\bf u}^{m+1}+\int_{t^{m+1}}^{t^{m}}\underline{\bf u}_{t}{\rm d}t, \underline{\bf u}^{m-1}=\underline{\bf u}^{m+1}+\int_{t^{m+1}}^{t^{m-1}}\underline{\bf u}_{t}{\rm d}t. \end{eqnarray*}$

代入并整理得

$\begin{eqnarray*} \frac{1}{\Delta t}A(\xi_{\underline{\bf u}}^{m+1},\theta) &=&\frac{1}{\Delta t}\left[(P_h^{\underline{\bf u}}-I) A(\underline{\bf u}^{m+1},\theta)\right]\\ &=&\frac{1}{\Delta t}\bigg[2(1-\theta)\int_{t^{m}}^{t^{m+1}}(P_h^{\underline{\bf u}}-I)\underline{\bf u}_{t}{\rm d}t -\frac{1-2\theta}{2}\int_{t^{m-1}}^{t^{m+1}}(P_h^{\underline{\bf u}}-I)\underline{\bf u}_{t}{\rm d}t\bigg]. \end{eqnarray*}$

从而

$\begin{eqnarray*}\label{E2} &&2\Delta t\left(\frac{1}{\Delta t}A(\xi_{\underline{\bf u}}^{m+1},\theta),B(\eta_{\underline{\bf u}}^{m+1},\theta)\right)\nonumber\\ &\leq& \frac{3\Delta t}{C_{coe}} \|\frac{1}{\Delta t}A(\xi_{\underline{\bf u}}^{m+1},\theta)\|^2_{\bf U'} +\frac{C_{coe}\Delta t}{3}\left\|B(\eta_{\underline{\bf u}}^{m+1},\theta)\right\|_{\bf U}^2\nonumber\\ &\leq& \frac{3(20\theta^2-36\theta+17)}{4C_{coe}} \int_{t^{m-1}}^{t^{m+1}}\|(P_h^{\underline{\bf u}}-I)\underline{\bf u}_t\|^2_{\bf U'}{\rm d}t +\frac{C_{coe}\Delta t}{3} \left\|B(\eta_{\underline{\bf u}}^{m+1},\theta)\right\|_{\bf U}^2. \end{eqnarray*}$

(4.7)

类似地, 根据积分型余项的泰勒展开式,有

$\begin{eqnarray*} & &{\bf F}^{m+1}={\bf F}^{m}+\Delta t{\bf F}_{t}^{m}+\int_{t^{m}}^{t^{m+1}}(t^{m+1}-t){\bf F}_{tt}{\rm d}t,\\ &&{\bf F}^{m-1}={\bf F}^{m}-\Delta t{\bf F}_{t}^{m}+\int_{t^{m}}^{t^{m-1}}(t^{m-1}-t){\bf F}_{tt}{\rm d}t, \end{eqnarray*}$

代入并整理得

$\begin{eqnarray*} F({\bf F}^{m+1},\theta) &=&-\frac{(1-\theta)(1-2\theta)}{2}\int_{t^m}^{t^{m+1}}(t^{m+1}-t){\bf F}_{tt}{\rm d}t\\ &&+\frac{(1-\theta)(1-2\theta)}{2}\int_{t^{m-1}}^{t^{m}}(t^{m-1}-t){\bf F}_{tt}{\rm d}t. \end{eqnarray*}$

从而

$\begin{matrix}\label{E3} &&2\Delta t\left(F({\bf F}^{m+1},\theta),B(\eta_{\underline{\bf u}}^{m+1},\theta)\right)\nonumber\\ &\leq &\frac{(1-\theta)^2(1-2\theta)^2\Delta t^4}{4C_{coe}}\int_{t^{m-1}}^{t^{m+1}} \|{\bf F}_{tt}\|_{\bf U'}^2{\rm d}t +\frac{C_{coe}\Delta t}{3}\left\|B(\eta_{\underline{\bf u}}^{m+1},\theta)\right\|_{\bf U}^2. \end{matrix}$

(4.8)

最后, 结合 (4.5)-(4.8) 式, 将 (4.4) 式从 $m=1$ 直到 $m=N-1$ 求和, 类似定理3.1的证明有

$\begin{eqnarray*} &&\frac{3-2\theta}{4(1-\theta)}\|\eta_{\underline{\bf u}}^{N}\|_0^2+C_{coe}\Delta t\sum_{m=1}^{N-1}\left\|B(\eta_{\underline{\bf u}}^{m+1},\theta)\right\|_{\bf U}^2\\ &\leq&\sum_{m=1}^{N-1} \bigg(\frac{ (60\theta^4-200\theta^3+257\theta^2-130\theta+24)\Delta t^4}{5C_{coe}} \int_{t^{m-1}}^{t^{m+1}}\|\underline{\bf u}_{ttt}\|^2_{\bf U'}{\rm d}t\\ &&+\frac{3(20\theta^2-36\theta+17)}{4C_{coe}} \int_{t^{m-1}}^{t^{m+1}}\|(P_h^{\underline{\bf u}}-I)\underline{\bf u}_t\|^2_{\bf U'}{\rm d}t +\frac{(1-\theta)^2(1-2\theta)^2\Delta t^4}{4C_{coe}} \int_{t^{m-1}}^{t^{m+1}} \|{\bf F}_{tt}\|_{\bf U'}^2{\rm d}t\bigg). \end{eqnarray*}$

由三角不等式可得耦合算法误差估计的结论. 证毕.

4.2 解耦算法的误差估计

${\bf定理4.2}$ (解耦算法的二阶收敛性) 在 (4.2) 和 (4.3) 式的假设下, 对于 $N\geq 2$ 有以下估计

$\begin{eqnarray*} &&\frac{3-2\theta}{4(1-\theta)}\|e_{{\bf u}_{f}}^{N}\|_f^2 +\hat{C}_{coe}\Delta t\sum_{m=1}^{N-1} \left\|B(e_{{\bf u}_f}^{m+1},\theta)\right\|_{{\bf H}_f}^2\\ &&+\frac{g(3-2\theta)}{4(1-\theta)}\|e_{\phi_{p}}^{N}\|_p^2 +g\check{C}_{coe}\Delta t\sum_{m=1}^{N-1} \left\|B(e_{{\phi}_p}^{m+1},\theta)\right\|_{{\bf H}_p}^2 \leq C (\Delta t^4+h^4). \end{eqnarray*}$

${\bf证}$ 在 $t_{m+1}$ , $t_{m}$ 和 $t_{m-1}$ 时刻分别对 (2.11) 式乘 $\frac{(1-\theta)(3-2\theta)}{2}$ , $(4\theta-1-2\theta^2)$ , $\frac{(1-\theta)(1-2\theta)}{2}$ 得到三个对应时刻的等式. 从 (3.16) 式中减去三者之和, 再结合误差函数的定义和投影算子的性质 (3.2) 式可得 $\forall$ ${\bf v}_{fh}\in {\bf H}_{fh}$ , $\psi_{ph}\in {\bf H}_{ph}$ , $q_{fh}\in Q_{fh}$ ,有

$\begin{eqnarray*} \label{Error d} &&\left(\frac{1}{\Delta t}A(\eta_{{\bf u}_f}^{m+1},\theta),{\bf v}_{fh}\right)_{\Omega_{f}} +a_{\Omega_f}\left(B(\eta_{{\bf u}_f}^{m+1},\theta),{\bf v}_{fh}\right) +b\left({\bf v}_{fh}, B(\eta_{p_f}^{m+1},\theta)\right)\nonumber\\ &&+g\left(\frac{1}{\Delta t}A(\eta_{{\phi}_p}^{m+1},\theta),\psi_{ph}\right)_{\Omega_{p}} +a_{\Omega_p}\left(B(\eta_{{\phi}_p}^{m+1},\theta),\psi_{ph}\right)\nonumber\\ &=&-\left(\frac{1}{\Delta t}A({\bf u}_f^{m+1},\theta)-B({\bf u}_t^{m+1},\theta),{\bf v}_{fh}\right)_{\Omega_{f}} -\left(\frac{1}{\Delta t}A(\xi_{{\bf u}_f}^{m+1},\theta),{\bf v}_{fh}\right)_{\Omega_{f}}\\ &&-g\left(\frac{1}{\Delta t}A(\phi_p^{m+1},\theta) -\frac{1}{\Delta t}B(\phi_t^{m+1},\theta),\psi_{ph}\right)_{\Omega_{p}} -g\left(\frac{1}{\Delta t}A(\xi_{{\phi}_p}^{m+1},\theta),\psi_{ph}\right)_{\Omega_{p}}\nonumber\\ &&+\left(F({\bf g}_f^{m+1},\theta),{\bf v}_{fh}\right)_{\Omega_{f}} +g\left(F({\bf g}_p^{m+1},\theta),\psi_{ph}\right)_{\Omega_{p}}\nonumber\\ &&-c_{\Gamma}\left({\bf v}_{fh},(2-\theta)\phi_{ph}^m-(1-\theta)\phi_{ph}^{m-1} -B(\phi_{p}^{m+1},\theta)\right)\nonumber\\ &&+c_{\Gamma}\left((2-\theta){\bf u}_{fh}^m-(1-\theta){\bf u}_{fh}^{m-1} -B({\bf u}_{f}^{m+1},\theta),\psi_{ph}\right),\nonumber\\ &&b\left(B(\eta_{{\bf u}_{f}}^{m+1},\theta), q_{fh}\right)=0.\nonumber \end{eqnarray*}$

(4.9)

假设 ${\bf v}_{fh}=2\Delta tB(\eta_{{\bf u}_f}^{m+1},\theta)$ , $\psi_{ph}=2\Delta tB(\eta_{{\phi}_p}^{m+1},\theta)$ , $q_{fh}=2\Delta tB(\eta_{{p}_f}^{m+1},\theta)$ . 回顾定理 4.1 的证明, 有以下不等式成立

$\begin{eqnarray*} && 2\left(A(\eta_{{u}_f}^{m+1},\theta), B(\eta_{{u}_f}^{m+1},\theta)\right)_{\Omega_{f}}\nonumber\\ &\geq & (2\theta^2-5\theta+3)\|\eta_{{u}_f}^{m+1}\|^2_f-2(1-\theta)\|\eta_{{u}_f}^{m}\|^2_f -(1-2\theta)(1-\theta)\|\eta_{{u}_f}^{m-1}\|^2_f\nonumber\\ &&-(1-2\theta)(3-2\theta)(\|\eta_{{u}_f}^{m+1}\|_f\|\eta_{{u}_f}^{m}\|_f -\|\eta_{{u}_f}^{m}\|_f\|\eta_{{u}_f}^{m-1}\|_f), \end{eqnarray*}$

(4.10)

$\begin{eqnarray*} &&2g\left(A(\eta_{{\phi}_p}^{m+1},\theta),B(\eta_{{\phi}_p}^{m+1},\theta)\right)_{\Omega_{p}}\nonumber\\ &\geq & g\left[(2\theta^2-5\theta+3)\|\eta_{{\phi}_p}^{m+1}\|^2_p-2(1-\theta)\|\eta_{{\phi}_p}^{m}\|^2_p -(1-2\theta)(1-\theta)\|\eta_{{\phi}_p}^{m-1}\|^2_p\right.\nonumber\\ &&\left.-(1-2\theta)(3-2\theta)(\|\eta_{{\phi}_p}^{m+1}\|_p\|\eta_{{\phi}_p}^{m}\|_p -\|\eta_{{\phi}_p}^{m}\|_p\|\eta_{{\psi}_p}^{m-1}\|_p)\right], \end{eqnarray*}$

(4.11)

$\begin{eqnarray*}\label{error221}&& 2\Delta t a_{\Omega_f}\left(B(\eta_{{u}_f}^{m+1},\theta),B(\eta_{{u}_f}^{m+1},\theta)\right) \geq 2\hat{C}_{coe}\Delta t \left\|B(\eta_{{u}_f}^{m+1},\theta)\right\|_{H_f}^2,\end{eqnarray*}$

(4.12)

$\begin{matrix} \label{error222} &&2\Delta t a_{\Omega_p}\left(B(\eta_{{\phi}_p}^{m+1},\theta),B(\eta_{{\phi}_p}^{m+1},\theta)\right) \geq 2g\check{C}_{coe}\Delta t \left\|B(\eta_{{\phi}_p}^{m+1},\theta)\right\|_{H_p}^2, \end{matrix}$

(4.13)

$\begin{eqnarray*}\label{error r211} &&2\Delta t\bigg(\frac{1}{\Delta t}A({\bf u}_f^{m+1},\theta)-B({\bf u}_t^{m+1},\theta), B(\eta_{{u}_f}^{m+1},\theta)\bigg)_{\Omega_{f}}\\ &\leq &\frac{\hat{C}_{coe}\Delta t}{6}\left\|B(\eta_{{u}_f}^{m+1},\theta)\right\|_{H_f}^2 +\frac{2(60\theta^4-200\theta^3+257\theta^2-130\theta+24)\Delta t^4}{5\hat{C}_{coe}} \int_{t^{m-1}}^{t^{m+1}}\|{\bf u}_{ttt}\|_{H_f'}^2{\rm d}t,\nonumber \end{eqnarray*}$

(4.14)

$\begin{aligned} & 2 g \Delta t\left(\frac{1}{\Delta t} A\left(\phi_{p}^{m+1}, \theta\right)-B\left(\phi_{t}^{m+1}, \theta\right), B\left(\eta_{\phi_{p}}^{m+1}, \theta\right)\right)_{\Omega_{p}} \\ \leq & \frac{g \check{C}_{c o e} \Delta t}{6}\left\|B\left(\eta_{\phi_{p}}^{m+1}, \theta\right)\right\|_{\mathbf{H}_{p}}^{2}+\frac{2 g\left(60 \theta^{4}-200 \theta^{3}+257 \theta^{2}-130 \theta+24\right) \Delta t^{4}}{5 \check{C}_{c o e}} \int_{t^{m-1}}^{t^{m+1}}\left\|\phi_{t t t}\right\|_{\mathbf{H}_{p}^{\prime}}^{2} \mathrm{~d} t \end{aligned}$

(4.15)

$\begin{eqnarray*}\label{error r221} &&2\Delta t \left(\frac{1}{\Delta t}A(\xi_{{u}_f}^{m+1},\theta),B(\eta_{{u}_f}^{m+1},\theta)\right)_{\Omega_{f}}\nonumber\\ &\leq &\frac{3(20\theta^2-36\theta+17)}{2\hat{C}_{coe}} \int_{t^{m-1}}^{t^{m+1}}\|(P_h^{{\bf u}_f}-I){\bf u}_t\|^2_{H_f'}{\rm d}t +\frac{\hat{C}_{coe}\Delta t}{6}\left\|B(\eta_{{u}_f}^{m+1},\theta)\right\|_{H_f}^2, \end{eqnarray*}$

(4.16)

$\begin{eqnarray*}\label{error r222} &&2g\Delta t\left(\frac{1}{\Delta t}A(\xi_{{\phi}_p}^{m+1},\theta), B(\eta_{{\phi}_p}^{m+1},\theta)\right)_{\Omega_{p}}\nonumber\\ &\leq& \frac{3g(20\theta^2-36\theta+17)}{2\check{C}_{coe}} \int_{t^{m-1}}^{t^{m+1}}\|(P_h^{{\phi}_p}-I)\phi_t\|^2_{H_p'}{\rm d}t +\frac{g\check{C}_{coe}\Delta t}{6}\left\|B(\eta_{{\phi}_p}^{m+1},\theta)\right\|_{H_p}^2, \end{eqnarray*}$

(4.17)

$\begin{eqnarray*} \label{error r231} &&2\Delta t\left(F({\bf g}_f^{m+1},\theta),B(\eta_{{u}_f}^{m+1},\theta)\right)_{\Omega_{f}}\nonumber\\ &\leq &\frac{(1-\theta)^2(1-2\theta)^2\Delta t^4}{2\hat{C}_{coe}}\int_{t^{m-1}}^{t^{m+1}} \|{\bf g}_{tt}\|_{H_f'}^2{\rm d}t+\frac{\hat{C}_{coe}\Delta t}{6}\left\|B(\eta_{{u}_f}^{m+1},\theta)\right\|_{H_f}^2, \end{eqnarray*}$

(4.18)

$\begin{eqnarray*}\label{error r232} &&2g\Delta t\left(F({\bf g}_p^{m+1},\theta),B(\eta_{{\phi}_p}^{m+1},\theta)\right)_{\Omega_{p}}\nonumber\\ &\leq &\frac{g(1-\theta)^2(1-2\theta)^2\Delta t^4}{2\check{C}_{coe}}\int_{t^{m-1}}^{t^{m+1}} \|{\bf g}_{tt}\|_{H_p'}^2{\rm d}t +\frac{g\check{C}_{coe}\Delta t}{6}\left\|B(\eta_{{\phi}_p}^{m+1},\theta)\right\|_{H_p}^2. \end{eqnarray*}$

(4.19)

下面主要分析交界面项. 交界面项可以被分解为

$\begin{eqnarray*} & &-2\Delta tc_{\Gamma} \left(B(\eta_{{\bf u}_f}^{m+1},\theta), (2-\theta)\phi_{ph}^m-(1-\theta)\phi_{ph}^{m-1} -B(\phi_{p}^{m+1},\theta)\right)\nonumber\\ &&+2\Delta tc_{\Gamma} \left((2-\theta){\bf u}_{fh}^m-(1-\theta){\bf u}_{fh}^{m-1} -B({\bf u}_{f}^{m+1},\theta),B(\eta_{{\phi}_p}^{m+1},\theta)\right)\nonumber\\ &=&-2\Delta tc_{\Gamma} \left(B(\eta_{{\bf u}_f}^{m+1},\theta),B(\eta_{\phi_{p}}^{m+1},\theta)\right) +2\Delta tc_{\Gamma} \left(B(\eta_{{\bf u}_{f}}^{m+1},\theta),B(\eta_{{\phi}_p}^{m+1},\theta)\right)\nonumber\\ &&-2\Delta tc_{\Gamma} \left(B(\eta_{{\bf u}_f}^{m+1},\theta),W(\eta_{{\phi}_p}^{m+1},\theta)\right) +2\Delta tc_{\Gamma} \left(W(\eta_{{\bf u}_{f}}^{m+1},\theta),B(\eta_{{\phi}_p}^{m+1},\theta)\right)\nonumber\\ &&-2\Delta tc_{\Gamma} \left(B(\eta_{{\bf u}_f}^{m+1},\theta),B(\xi_{\phi_{p}}^{m+1},\theta)\right) +2\Delta tc_{\Gamma} \left(B(\xi_{{\bf u}_{f}}^{m+1},\theta),B(\eta_{\phi_{p}}^{m+1},\theta)\right)\nonumber\\ &&-2\Delta tc_{\Gamma} \left(B(\eta_{{\bf u}_f}^{m+1},\theta),W(\xi_{\phi_{p}}^{m+1},\theta)\right) +2\Delta tc_{\Gamma} \left(W(\xi_{{\bf u}_{f}}^{m+1},\theta),B(\eta_{\phi_{p}}^{m+1},\theta)\right)\nonumber\\ &&-2\Delta tc_{\Gamma} \left(B(\eta_{{\bf u}_f}^{m+1},\theta),W(\phi_{p}^{m+1},\theta)\right) +2\Delta tc_{\Gamma} \left(W({\bf u}_{f}^{m+1},\theta),B(\eta_{\phi_{p}}^{m+1},\theta)\right). \end{eqnarray*}$

(4.20)

由线性性质可知, 上式中前四项之和等于 $0$ . 下面四项借助 (2.12) 式及引理 3.2, 并代入 $\varepsilon_3=\varepsilon_5=\frac{3}{\hat{C}_{coe}}$ , $\varepsilon_4=\varepsilon_6=\frac{3g}{\check{C}_{coe}}$ , 有

$\begin{eqnarray*}\label{E42} &&-2\Delta tc_{\Gamma} \left(B(\eta_{{\bf u}_f}^{m+1},\theta),B(\xi_{\phi_{p}}^{m+1},\theta)\right) +2\Delta tc_{\Gamma} \left(B(\xi_{{\bf u}_{f}}^{m+1},\theta),B(\eta_{\phi_{p}}^{m+1},\theta)\right)\nonumber\\ &&-2\Delta tc_{\Gamma} \left(B(\eta_{{\bf u}_f}^{m+1},\theta),W(\xi_{\phi_{p}}^{m+1},\theta)\right) +2\Delta tc_{\Gamma} \left(W(\xi_{{\bf u}_{f}}^{m+1},\theta),B(\eta_{\phi_{p}}^{m+1},\theta)\right)\nonumber\\ &\leq &\frac{\hat{C}_{coe}\Delta t}{6} \left\|B(\eta_{{\bf u}_f}^{m+1},\theta)\right\|_{{\bf H}_f}^2 +\frac{6C_3h^{-1}\Delta t}{\hat{C}_{coe}} \left\|B(\xi_{\phi_{p}}^{m+1},\theta)\right\|_p^2\nonumber\\ &&+\frac{g\check{C}_{coe}\Delta t}{6} \left\|B(\eta_{\phi_{p}}^{m+1},\theta)\right\|_{{\bf H}_p}^2 +\frac{6gC_4h^{-1}\Delta t}{\check{C}_{coe}} \left\|B(\xi_{{\bf u}_{f}}^{m+1},\theta)\right\|_f^2\nonumber\\ &&+\frac{\hat{C}_{coe}\Delta t}{6} \left\|B(\eta_{{\bf u}_f}^{m+1},\theta)\right\|_{{\bf H}_f}^2 +\frac{6C_5h^{-1}\Delta t}{\hat{C}_{coe}} \left\|W(\xi_{\phi_{p}}^{m+1},\theta)\right\|_p^2\nonumber\\ & &+\frac{g\check{C}_{coe}\Delta t}{6} \left\|B(\eta_{\phi_{p}}^{m+1},\theta)\right\|_{{\bf H}_p}^2 +\frac{6gC_6h^{-1}\Delta t}{\check{C}_{coe}} \left\|W(\xi_{{\bf u}_{f}}^{m+1},\theta)\right\|_f^2\nonumber\\ &\leq &\frac{\hat{C}_{coe}\Delta t}{3} \left\|B(\eta_{{\bf u}_f}^{m+1},\theta)\right\|_{{\bf H}_f}^2 +\frac{g\check{C}_{coe}\Delta t}{3} \left\|B(\eta_{\phi_{p}}^{m+1},\theta)\right\|_{{\bf H}_p}^2\nonumber\\ &&+\frac{6g\Delta t}{\hat{C}_{coe}} \left\|B(\xi_{\phi_{p}}^{m+1},\theta)\right\|_p^2 +\frac{6\Delta t}{\check{C}_{coe}} \left\|B(\xi_{{\bf u}_{f}}^{m+1},\theta)\right\|_f^2\nonumber\\ &&+\frac{6g\Delta t}{\hat{C}_{coe}} \left\|W(\xi_{\phi_{p}}^{m+1},\theta)\right\|_p^2 +\frac{6\Delta t}{\check{C}_{coe}} \left\|W(\xi_{{\bf u}_{f}}^{m+1},\theta)\right\|_f^2, \end{eqnarray*}$

(4.21)

其中, 最后一个不等式是在选择合适的常量 $C_3,C_4,C_5$ 和 $C_6$ 下得到的.

利用带有积分型余项的泰勒展开式,有

$\begin{eqnarray*} & &\phi_p^{m+1}=\phi_p^{m}+\Delta t\phi_{t}^{m}+\int_{t^{m}}^{t^{m+1}}(t^{m+1}-t)\phi_{tt}{\rm d}t,\qquad\\ &&\phi_p^{m-1}=\phi_p^{m}-\Delta t\phi_{t}^{m}+\int_{t^{m}}^{t^{m-1}}(t^{m-1}-t)\phi_{tt}{\rm d}t, \end{eqnarray*}$

代入并整理得

$\begin{eqnarray*} W(\phi_{p}^{m+1},\theta) &=&-\frac{(1-\theta)(3-2\theta)}{2}\int_{t^m}^{t^{m+1}}(t^{m+1}-t)\phi_{tt}{\rm d}t\\ &&+\frac{(1-\theta)(3-2\theta)}{2}\int_{t^{m-1}}^{t^{m}}(t^{m-1}-t)\phi_{tt}{\rm d}t, \end{eqnarray*}$

类似地, 根据带有积分型余项的泰勒展开式,有

$\begin{eqnarray*} & &{\bf u}_f^{m+1}={\bf u}_f^{m}+\Delta t{\bf u}_{t}^{m}+\int_{t^{m}}^{t^{m+1}}(t^{m+1}-t){\bf u}_{tt}{\rm d}t,\qquad\\ &&{\bf u}_f^{m-1}={\bf u}_f^{m}-\Delta t{\bf u}_{t}^{m}+\int_{t^{m}}^{t^{m-1}}(t^{m-1}-t){\bf u}_{tt}{\rm d}t, \end{eqnarray*}$

可以得到

$\begin{eqnarray*} W({\bf u}_{f}^{m+1},\theta) &=&-\frac{(1-\theta)(3-2\theta)}{2}\int_{t^m}^{t^{m+1}}(t^{m+1}-t){\bf u}_{tt}{\rm d}t\\ &&+\frac{(1-\theta)(3-2\theta)}{2}\int_{t^{m-1}}^{t^{m}}(t^{m-1}-t){\bf u}_{tt}{\rm d}t. \end{eqnarray*}$

利用引理 3.2 并代入 $\varepsilon_7=\frac{3}{\hat{C}_{coe}},\varepsilon_8=\frac{3g}{\check{C}_{coe}}$ 可得

$\begin{eqnarray*} &&-2\Delta tc_{\Gamma} \left(B(\eta_{{\bf u}_f}^{m+1},\theta),W(\phi_{p}^{m+1},\theta)\right) +2\Delta tc_{\Gamma} \left(W({\bf u}_{f}^{m+1},\theta),B(\eta_{\phi_{p}}^{m+1},\theta)\right)\nonumber\\ &\leq &\frac{\hat{C}_{coe}\Delta t}{6} \left\|B(\eta_{{\bf u}_f}^{m+1},\theta)\right\|_{{\bf H}_f}^2 +\frac{6C_7h^{-1}\Delta t}{\hat{C}_{coe}} \left\|W(\phi_{p}^{m+1},\theta)\right\|_p^2\nonumber\\ &&+\frac{g\check{C}_{coe}\Delta t}{6} \left\|B(\eta_{\phi_{p}}^{m+1},\theta)\right\|_{{\bf H}_p}^2 +\frac{6gC_8h^{-1}\Delta t}{\check{C}_{coe}} \left\|W({\bf u}_{f}^{m+1},\theta)\right\|_f^2\nonumber\\ &\leq &\frac{\hat{C}_{coe}\Delta t}{6} \left\|B(\eta_{{\bf u}_f}^{m+1},\theta)\right\|_{{\bf H}_f}^2 +\frac{6g\Delta t}{\hat{C}_{coe}} \left\|W(\phi_{p}^{m+1},\theta)\right\|_p^2\nonumber\\ &&+\frac{g\check{C}_{coe}\Delta t}{6} \left\|B(\eta_{\phi_{p}}^{m+1},\theta)\right\|_{{\bf H}_p}^2 +\frac{6\Delta t}{\check{C}_{coe}} \left\|W({\bf u}_{f}^{m+1},\theta)\right\|_f^2\nonumber\\ &\leq &\frac{\hat{C}_{coe}\Delta t}{6} \left\|B(\eta_{{\bf u}_f}^{m+1},\theta)\right\|_{{\bf H}_f}^2 +\frac{\check{C}_{coe}\Delta t}{6} \left\|B(\eta_{\phi_{p}}^{m+1},\theta)\right\|_{{\bf H}_p}^2\nonumber\\ &&+\frac{(1-\theta)^2(3-2\theta)^2\Delta t^{4}}{2\check{C}_{coe}}\int_{t^{m-1}}^{t^{m+1}}\|{\bf u}_{tt}\|_f^2{\rm d}t +\frac{g(1-\theta)^2(3-2\theta)^2\Delta t^{4}}{2\hat{C}_{coe}}\int_{t^{m-1}}^{t^{m+1}}\|\phi_{tt}\|_p^2{\rm d}t, \end{eqnarray*}$

(4.22)

其中, 第二个不等式是在选择合适的常量 $C_7$ 和 $C_8$ 下得到的.

综上, 交界面项可化简为

$\begin{eqnarray*}\label{E4} &&-2\Delta tc_{\Gamma} \left(B(\eta_{{\bf u}_f}^{m+1},\theta), (2-\theta)\phi_{ph}^m-(1-\theta)\phi_{ph}^{m-1} -B(\phi_{p}^{m+1},\theta)\right)\nonumber\\ &&+2\Delta tc_{\Gamma} \left((2-\theta){\bf u}_{fh}^m-(1-\theta){\bf u}_{fh}^{m-1} -B({\bf u}_{f}^{m+1},\theta),B(\eta_{{\phi}_p}^{m+1},\theta)\right)\nonumber\\ &\leq &\frac{\hat{C}_{coe}\Delta t}{2} \left\|B(\eta_{{\bf u}_f}^{m+1},\theta)\right\|_{{\bf H}_f}^2 +\frac{g\check{C}_{coe}\Delta t}{2} \left\|B(\eta_{\phi_{p}}^{m+1},\theta)\right\|_{{\bf H}_p}^2\nonumber\\ &&+\frac{6g\Delta t}{\hat{C}_{coe}} \left\|B(\xi_{\phi_{p}}^{m+1},\theta)\right\|_p^2 +\frac{6\Delta t}{\check{C}_{coe}} \left\|B(\xi_{{\bf u}_{f}}^{m+1},\theta)\right\|_f^2\nonumber\\ &&+\frac{6g\Delta t}{\hat{C}_{coe}} \left\|W(\xi_{\phi_{p}}^{m+1},\theta)\right\|_p^2 +\frac{6\Delta t}{\check{C}_{coe}} \left\|W(\xi_{{\bf u}_{f}}^{m+1},\theta)\right\|_f^2\nonumber\\ &&+\frac{(1-\theta)^2(3-2\theta)^2\Delta t^{4}}{2\check{C}_{coe}}\int_{t^{m-1}}^{t^{m+1}}\|{\bf u}_{tt}\|_f^2{\rm d}t +\frac{g(1-\theta)^2(3-2\theta)^2\Delta t^{4}}{2\hat{C}_{coe}}\int_{t^{m-1}}^{t^{m+1}}\|\phi_{tt}\|_p^2{\rm d}t. \end{eqnarray*}$

(4.23)

结合 (4.10)-(4.23) 式, 将 (4.9) 式从 $m=1$ 直到 $m=N-1$ 求和, 类似定理 3.2 的证明, 有

$\begin{eqnarray*} &&\frac{3-2\theta}{4(1-\theta)}\|\eta_{\bf u}^{N}\|_f^2 +\hat{C}_{coe}\Delta t\sum_{m=1}^{N-1} \left\|B(\eta_{{\bf u}_f}^{m+1},\theta)\right\|_{{\bf H}_f}^2\\ &&+\frac{g(3-2\theta)}{4(1-\theta)}\|\eta_{\phi}^{N}\|_p^2 +g\check{C}_{coe}\Delta t\sum_{m=1}^{N-1} \left\|B(\eta_{\phi_{p}}^{m+1},\theta)\right\|_{{\bf H}_p}^2\\ &\leq &\sum_{m=1}^{N-1}\bigg( \frac{2(60\theta^4-200\theta^3+257\theta^2-130\theta+24) \Delta t^4}{5\hat{C}_{coe}} \int_{t^{m-1}}^{t^{m+1}}\|{\bf u}_{ttt}\|_{{\bf H}_f'}^2{\rm d}t\\ &&+\frac{2(60\theta^4-200\theta^3+257\theta^2-130\theta+24) g\Delta t^4}{5\check{C}_{coe}} \int_{t^{m-1}}^{t^{m+1}}\|\phi_{ttt}\|_{{\bf H}_p'}^2{\rm d}t\\ &&+\frac{3(20\theta^2-36\theta+17)}{2\hat{C}_{coe}} \int_{t^{m-1}}^{t^{m+1}}\|(P_h^{{\bf u}_f}-I){\bf u}_t\|^2_{{\bf H}_f'}{\rm d}t\\ &&+\frac{3g(20\theta^2-36\theta+17)}{2\check{C}_{coe}} \int_{t^{m-1}}^{t^{m+1}}\|(P_h^{{\phi}_p}-I)\phi_t\|^2_{{\bf H}_p'}{\rm d}t\\ &&+\frac{(1-\theta)^2(1-2\theta)^2\Delta t^4}{2\hat{C}_{coe}}\int_{t^{m-1}}^{t^{m+1}} \|{\bf g}_{tt}\|_{{\bf H}_f'}^2{\rm d}t +\frac{g(1-\theta)^2(1-2\theta)^2\Delta t^4}{2\check{C}_{coe}}\int_{t^{m-1}}^{t^{m+1}} \|{\bf g}_{tt}\|_{{\bf H}_p'}^2{\rm d}t\\ &&+\frac{(1-\theta)^2(3-2\theta)^2\Delta t^{4}}{2\check{C}_{coe}}\int_{t^{m-1}}^{t^{m+1}}\|{\bf u}_{tt}\|_f^2{\rm d}t +\frac{g(1-\theta)^2(3-2\theta)^2\Delta t^{4}}{2\hat{C}_{coe}}\int_{t^{m-1}}^{t^{m+1}}\|\phi_{tt}\|_p^2{\rm d}t\\ &&+\frac{6g\Delta t}{\hat{C}_{coe}} \left\|B(\xi_{\phi_{p}}^{m+1},\theta)\right\|_p^2 +\frac{6\Delta t}{\check{C}_{coe}} \left\|B(\xi_{{\bf u}_{f}}^{m+1},\theta)\right\|_f^2\\ &&+\frac{6g\Delta t}{\hat{C}_{coe}} \left\|W(\xi_{\phi_{p}}^{m+1},\theta)\right\|_p^2 +\frac{6\Delta t}{\check{C}_{coe}} \left\|W(\xi_{{\bf u}_{f}}^{m+1},\theta)\right\|_f^2\bigg). \end{eqnarray*}$

由三角不等式可得解耦算法误差估计的结论.证毕.

5 数值实验

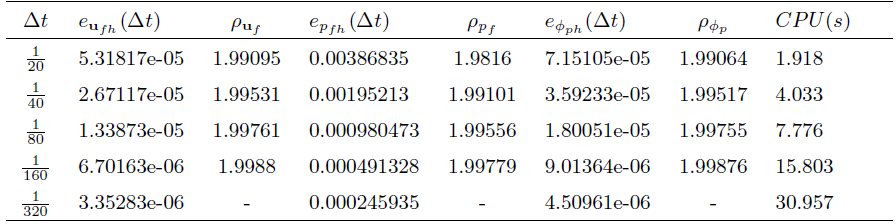
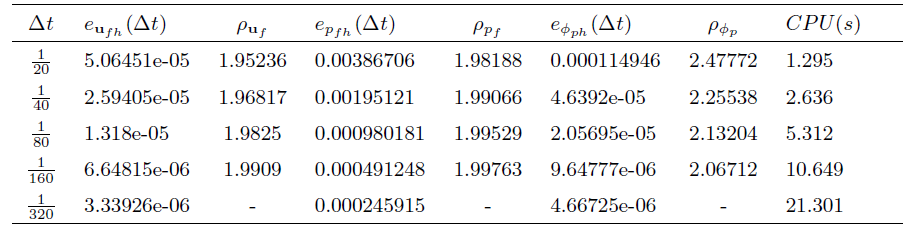
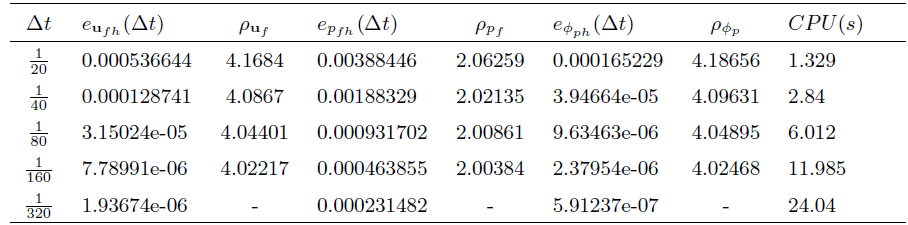
这一节将进行3个数值实验. 第1个实验对耦合和解耦算法的有效性进行模拟. 第2个实验说明算法的收敛阶由一阶提高到二阶, 并通过对比体现出解耦算法的高效性. 第3个实验将耦合和解耦的向后欧拉方法和取不同 $\theta$ 值的线性多步法, 以及在此基础上加 time filter 算法进行比较, 说明了线性多步法和线性多步法加 time filter 算法的误差相对较小. 本文的数值模拟是利用 FreeFEM++ 软件实现的. 并不失一般性, 以下实验均假设相应的物理参数 $\nu=1$ , $\rho=1$ , $g=1$ , $S=1$ $\alpha=1$ 以及 ${\bf K}=k{\bf I}$ , 其中 $k=1$ . 并且所有的初始条件, 边界条件和源项遵循精确解. 为了简便, 在图例, 图注及表头中, CBEM 和 DBEM 分别表示耦合和解耦的向后欧拉方法, CLMM 和 DLMM 分别表示耦合和解耦的线性多步法, CBEMTF 和 DBEMTF 分别表示耦合和解耦的向后欧拉方法加 time filter 算法, CLMMTF 和 DLMMTF 分别表示耦合和解耦的线性多步法加 time filter 算法.

${\bf 实验 1}$ 这里利用文献[37] 中的算例，设全局区域 $\Omega$ 由不可压缩流区域 $\Omega_f=(0,\pi)\times(0,1)$ , 多孔介质区域 $\Omega_p=(0,\pi)\times(-1,0)$ , 以及交界面 $\Gamma=(0,\pi)\times{0}$ 组成. Taylor-Hood 元 (P2-P1) 和分段二次多项式 (P2) 被用于自由流体流动方程和多孔介质流动方程. 精确解由下式给出

$\begin{eqnarray*} &&{\bf u}_f=\bigg[\frac{1}{\pi}\sin(2\pi y)\cos(x)e^t, (-2+\frac{1}{\pi^2}\sin^2(\pi y))\sin(x)e^t\bigg],\\ &&p_f=0,\\ &&\phi_p=(e^y-e^{-y})\sin(x)e^t. \end{eqnarray*}$

为验证算法的有效性, 本文设置网格尺寸为 $h=1/100$ , 时间步长为 0.01 进行数值模拟. 图 2-图 4 分别展示了 $\theta=1/6$ , $1/4$ , $1/3$ 耦合和解耦的线性多步法以及线性多步法加 time filter 算法的速度等值线和速度流线, 通过观察可以发现本文提出的算法能够有效地模拟流体的流动.

图 2

图 2 $\theta=1/6$ 时, 速度等值线和速度流线

图 3

图 3 $\theta=1/4$ 时, 速度等值线和速度流线

图 4

图 4 $\theta=1/3$ 时, 速度等值线和速度流线

${\bf 实验 2}$ 这里借助文献[31]中的算例, 考虑不可压缩流区域 $\Omega_f=(0,1)\times(1,2)$ , 多孔介质区域 $\Omega_p=(0,1)\times(0,1)$ , 以及交界面 $\Gamma=(0,1)\times{1}$ , 并对自由流体流动方程和多孔介质流动方程分别使用 MINI 元 (P1b-P1) 和线性拉格朗日元 (P1). 下面给出精确解

$\begin{eqnarray*} &&{\bf u}_f=((x^2(y-1)^2+y)\cos(t),-\frac{2}{3}x(y-1)^3\cos(t)+(2-\pi\sin(\pi x))\cos(t)),\\ &&p_f=(2-\pi\sin(\pi x))\sin(\frac{1}{2}\pi y)\cos(t),\\ &&\phi_p=(2-\pi\sin(\pi x))(1-y-\cos(\pi y))\cos(t). \end{eqnarray*}$

为体现耦合和解耦算法的收敛阶, 本实验考虑 $\theta=1/4$ , 并在表1-表8 中分别列出变化时间步长 $\Delta t$ 和网格尺寸 $h$ 对应的误差, 收敛阶及CPU 时间.

表1 $T=1$ 时, 固定网格尺寸 $h=\frac{1}{8}$ , 随时间步长 $\Delta t$ 变化 CLMM 计算所得结果

表2 $T=1$ 时, 固定网格尺寸 $h=\frac{1}{8}$ , 随着时间步长 $\Delta t$ 变化 CLMMTF 计算所得结果

表3 $T=1$ 时, 固定网格尺寸 $h=\frac{1}{8}$ , 随着时间步长 $\Delta t$ 变化 DLMM 计算所得结果

表4 $T=1$ 时, 固定网格尺寸 $h=\frac{1}{8}$ , 随着时间步长 $\Delta t$ 变化 DLMMTF 计算所得结果

表5 $T=1$ 时, 固定时间步长 $\Delta t=0.01$ , 随着网格尺寸 $h$ 变化 CLMM 计算所得结果

表6 $T=1$ 时, 固定时间步长 $\Delta t=0.01$ , 随着网格尺寸 $h$ 变化 CLMMTF 计算所得结果

表7 $T=1$ 时, 固定时间步长 $\Delta t=0.01$ , 随着网格尺寸 $h$ 变化 DLMM 计算所得结果

表8 $T=1$ 时, 固定时间步长 $\Delta t=0.01$ , 随着网格尺寸 $h$ 变化 DLMMTF 计算所得结果

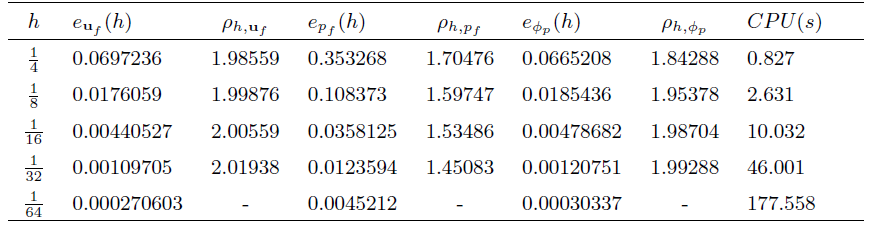
首先, 利用与文献[31] 中相同的方法, 通过固定网格尺寸 $h$ , 变化时间步长 $\Delta t$ 计算耦合和解耦算法的收敛阶. 这时近似误差主要由时间步长 $\Delta t$ 控制. 定义

$\rho_{v}=\frac{e_{v}(\Delta t)}{e_{v}(\frac{1}{2}\Delta t)},$

其中 $e_{v}(\Delta t)=\|v_h^{\Delta t}-v_h^{\frac{1}{2}\Delta t}\|_{L^2}$ , $v={\bf u}_f$ , $\phi_p$ , $p_f$ , $\rho_{v}\approx \frac{4^{\gamma}-2^{\gamma}}{2^{\gamma}-1}$ . 固定网格尺寸 $h=\frac{1}{8}$ , 时间步长 $\Delta t$ 由 $\frac{1}{20}$ 变化到 $\frac{1}{320}$ 得到表 1 -表 4. 将表1 和表2, 表 3 和表4分别进行比较, 发现耦合和解耦的线性多步法是一阶收敛的, 而本文提出的线性多步法加 time filter 算法在几乎不增加计算量的情况下可以达到二阶收敛. 这体现了 time filter 算法的二阶收敛性和高效性. 同时通过比较表中 CPU 时间可以发现解耦算法的计算效率相对较高.

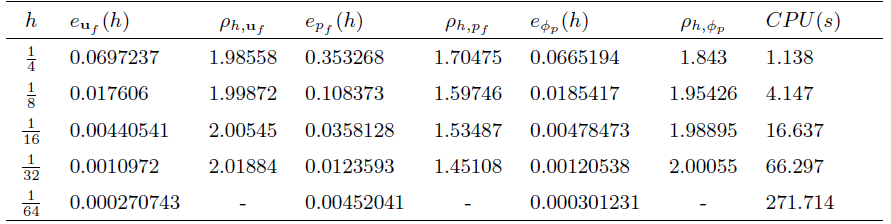
其次, 在固定时间步长 $\Delta t$ , 变化网格尺寸 $h$ 的情况下, 计算耦合和解耦算法的收敛阶. 这时近似误差主要由时间步长 $h$ 控制. 定义

$\rho_{h,v}=\frac{\log(\frac{e_{v}(h_1)}{e_{v}(h_2)})}{\log(\frac{h_1}{h_2})}$

其中 $e_{v}(h)=\|v_{f}-v_{fh}\|_{L^2}$ 是关于网格尺寸 $h$ 的误差. 固定时间步长 $\Delta t=0.01$ , 网格尺寸 $h$ 由 $\frac{1}{4}$ 变化到 $\frac{1}{64}$ 得到表 5 -表 8. 将表 5 和表 7, 表6 和表 8 中的 CPU 时间分别进行比较, 可以看出解耦算法所用的 CPU 时间较少, 计算效率相较于耦合算法较高.

${\bf 实验 3}$ 这里, 利用文献 [38-39] 中的算例进行数值实验. 同时选择与实验 2 中相同的区域 $\Omega_f$ 和 $\Omega_p$ , 以及有限元. 该精确解是

$\begin{eqnarray*} &&{\bf u}_f=((y^2-2y+1)\cos(t),(x^2-x)\cos(t)),\\ &&p_f=[2\nu(x+y-1)+\frac{1}{3k}]\cos(t),\\ &&\phi_p=[\frac{1}{k}(x(1-x)(y-1)+\frac{1}{3}y^3-y^2+y)+2\nu x]\cos(t). \end{eqnarray*}$

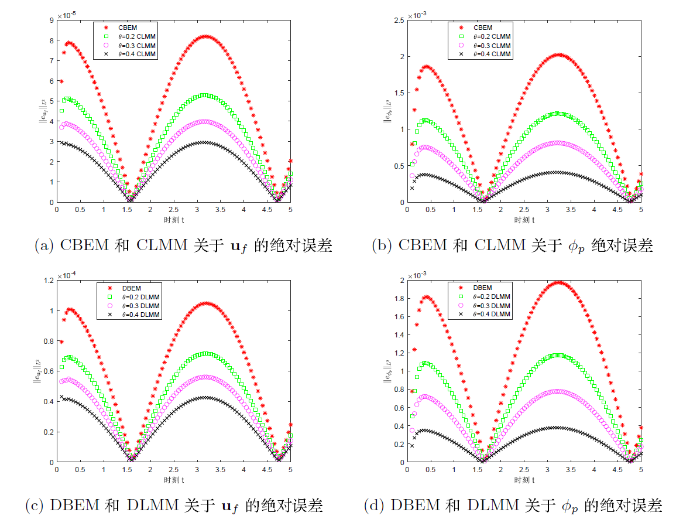
图 5 分别给出了向后欧拉方法和 $\theta$ 取不同值的线性多步法在时间段为 $[T]$ ( $T=5$ ) 且时间步长为 $0.05$ 上 ${\bf u}_f$ 和 $\phi_p$ 在每个时刻的绝对误差. 从图 5 中可以看出: 与向后欧拉方法相比较, 线性多步法关于 ${\bf u}_f$ 和 $\phi_p$ 的绝对误差几乎在每个时刻都相对较小. 同时, 当 $\theta$ 取不同值时线性多步法的绝对误差会随着 $\theta$ 的增大而减小. 类似地, 图 6 分别给出了向后欧拉方法加 time filter 算法和 $\theta$ 取不同值的线性多步法加 time filter 算法在时间段为 $[T]$ ( $T=5$ ) 且时间步长为 $0.05$ 上 ${\bf u}_f$ 和 $\phi_p$ 在每个时刻的绝对误差. 由图 6 知: 与向后欧拉方法加 time filter 算法相比, 无论是耦合还是解耦线性多步法加 time filter 算法关于 ${\bf u}_f$ 和 $\phi_p$ 的绝对误差几乎在每个时刻都相对较小, 同时随着 $\theta$ 的增大, 线性多步法加 time filter 的绝对误差减小.

图 5

图 5 向后欧拉方法和线性多步法的 ${\bf u}_f$ , $\phi_p$ 的绝对误差

图 6

图 6 向后欧拉方法加 time filter 算法和线性多步法加 time filter 算法的 ${\bf u}_f$ , $\phi_p$ 的绝对误差

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Ervin

V J

Approximation of coupled Stokes-Darcy flow in an axisymmetric domain

Computer Methods in Applied Mechanics and Engineering, 2013, 258: 96-108

DOI:10.1016/j.cma.2013.02.004 URL [本文引用: 1]

[2]

Hou

Y R

, Qin

On the solution of coupled Stokes/Darcy model with Beavers-Joseph interface condition

Computers & Mathematics with Applications, 2019, 77(1): 50-65

DOI:10.1016/j.camwa.2018.09.011 URL [本文引用: 1]

[3]

Cao

Y Z

, Gunzburger

, Hu

X L

, et al.

Finite element approximations for Stokes-Darcy flow with Beavers-Joseph interface conditions

SIAM Journal on Numerical Analysis, 2010, 47(6): 4239-4256

DOI:10.1137/080731542 URL [本文引用: 1]

[4]

Kanschat

, Riviére

A strongly conservative finite element method for the coupling of Stokes and Darcy flow

Journal of Computational Physics, 2010, 229(17): 5933-5943

DOI:10.1016/j.jcp.2010.04.021 URL [本文引用: 1]

[5]

Glowinshi

Finite element methods for incompressible viscous flow

Handbook of Numerical Analysis, 2003, 9: 3-1176

[6]

Lipnikov

, Vassilev

, Yotov

Discontinuous Galerkin and mimetic finite difference methods for coupled Stokes-Darcy flows on polygonal and polyhedral grids

Numerische Mathematik, 2014, 126(2): 321-360

DOI:10.1007/s00211-013-0563-3 URL [本文引用: 1]

[7]

Chen

W B

, Wang

Y Q

Weak Galerkin method for the coupled Darcy-Stokes flow

IMA Journal of Numerical Analysis, 2016, 36(2): 897-921

DOI:10.1093/imanum/drv012 URL [本文引用: 1]

[8]

Girault

, Riviére

DG approximation of coupled Navier-Stokes and Darcy equations by Beaver-Joseph-Saffman interface condition

SIAM Journal on Numerical Analysis, 2009, 47(3): 2052-2089

DOI:10.1137/070686081 URL [本文引用: 1]

[9]

Markus

, Houstis

E N

, Catlin

A C

, et al.

An agent-based netcentric framework for multidisciplinary problem solving environments (MPSE)

Inter J Comput Engineering Sci, 2000, 1(1): 33-60

DOI:10.33545/26633582 URL [本文引用: 1]

[10]

Solving composite problems with interface relaxation

SIAM Journal on Scientific Computing, 1999, 20(4): 1394-1416

DOI:10.1137/S1064827597321180 URL [本文引用: 1]

[11]

Gatica

G N

, Oyarzúa

, Sayas

F J

A residual-based a posteriori error estimator for a fully-mixed formulation of the Stokes-Darcy coupled problem

Computer Methods in Applied Mechanics and Engineering, 2011, 200(21/22): 1877-1891

DOI:10.1016/j.cma.2011.02.009 URL [本文引用: 1]

[12]

Layton

W J

, Schieweck

, Yotov

Coupling fluid flow with porous media flow

SIAM Journal on Numerical Analysis, 2002, 40(6): 2195-2218

DOI:10.1137/S0036142901392766 URL [本文引用: 1]

[13]

X M

, Li

, Lin

Y P

, et al.

A domain decomposition method for the steady-state Navier-Stokes-Darcy model with Beavers-Joseph interface condition

SIAM J Sci Comput, 2015, 37(5): S264-S290

DOI:10.1137/140965776 URL [本文引用: 1]

[14]

Cao

Y Z

, Gunzburger

, He

X M

, et al.

Robin-Robin domain decomposition methods for the steady Stokes-Darcy model with Beaver-Joseph interface condition

Numer Math, 2011, 117(4): 601-629

DOI:10.1007/s00211-011-0361-8 URL [本文引用: 1]

[15]

Chen

W B

, Gunzburger

, Hua

, et al.

A parallel Robin-Robin domain decomposition method for the Stokes-Darcy system

SIAM Journal on Numerical Analysis, 2011, 49(3): 1064-1084

DOI:10.1137/080740556 URL [本文引用: 1]

[16]

Hou

Y R

Optimal error estimates of a decoupled scheme based on two-grid finite element for mixed Stokes-Darcy model

Applied Mathematics Letters, 2016, 57: 90-96

DOI:10.1016/j.aml.2016.01.007 URL [本文引用: 1]

[17]

Qin

, Hou

Y R

Optimal error estimates of a decoupled scheme based on two-grid finite element for mixed Navier-Stokes/Darcy model

Acta Mathematica Scientia, 2018, 38(4): 1361-1369

DOI:10.1016/S0252-9602(18)30819-1 URL [本文引用: 1]

[18]

Zuo

L Y

, Du

G Z

A multi-grid technique for coupling fluid flow with porous media flow

Computers & Mathematics with Applications, 2018, 75(11): 4012-4021

DOI:10.1016/j.camwa.2018.03.010 URL [本文引用: 1]

[19]

Zuo

L Y

, Hou

Y R

A two-grid decoupling method for the mixed Stokes-Darcy model

Journal of Computational and Applied Mathematics, 2015, 275: 139-147

DOI:10.1016/j.cam.2014.08.008 URL [本文引用: 1]

[20]

Cao

Y Z

, Gunzburger

, Hua

, et al.

Coupled Stokes-Darcy model with Beavers-Joseph interface boundary condition

Communications in Mathematical Sciences, 2010, 8(1): 1-25

DOI:10.4310/CMS.2010.v8.n1.a2 URL [本文引用: 1]

[21]

Cao

Y Z

, Gunzburger

, He

X M

, et al.

Parallel, non-iterative, multi-physics domain decomposition methods for time-dependent Stokes-Darcy systems

Math Comput, 2014, 83(288): 1617-1644

DOI:10.1090/mcom/2014-83-288 URL [本文引用: 1]

[22]

Cao

Y Z

, Gunzburger

, Hu

X L

, et al.

Finite element approximation for time-dependent Stokes-Darcy flow with Beavers-Joseph interface boundary condition

SIAM J Numer Anal, 2010, 47(6): 4239-4256

DOI:10.1137/080731542 URL [本文引用: 1]

[23]

, Hou

Y R

A second-order partitioned method with different subdomain time steps for the evolutionary Stokes-Darcy system

Mathematical Methods in the Applied Sciences, 2018, 41(5): 2178-2208

DOI:10.1002/mma.v41.5 URL [本文引用: 1]

[24]

Layton

W J

, Tran

, Xiong

Long time stability of four methods for splitting the evolutionary Stokes-Darcy problem into Stokes and Darcy subproblems

Journal of Computational and Applied Mathematics, 2012, 236(13): 3198-3217

DOI:10.1016/j.cam.2012.02.019 URL [本文引用: 1]

[25]

Layton

W J

, Tran

, Trenchea

Analysis of long time stability and errors of two partitioned methods for uncoupling evolutionary groundwater-surface water flows

SIAM J Numer Anal, 2013, 51(1): 248-272

DOI:10.1137/110834494 URL [本文引用: 1]

[26]

Shan

, Zheng

H B

, Layton

W J

A decoupling method with different subdomain time steps for the nonstationary Stokes-Darcy model

Numer Meth Partial Differ Equ, 2013, 29(2): 549-583

DOI:10.1002/num.v29.2 URL [本文引用: 1]

[27]

Guzel

, Layton

W J

Time filters increase accuracy of the fully implicit method

BIT Numerical Mathematic, 2018, 58(2): 301-315

[28]

, Hou

Y R

, Layton

W J

Adaptive partitioned methods for the time-accurate approximation of the evolutionary Stokes-Darcy system

Computer Meth Appl Mech Engineering, 2020, 364: 112923

DOI:10.1016/j.cma.2020.112923 URL [本文引用: 1]

[29]

Qin

, Hou

Y R

The time filter for the non-stationary coupled Stokes/Darcy model

Applied Numerical Mathematics, 2019, 146: 260-275

DOI:10.1016/j.apnum.2019.07.015 [本文引用: 1]

In this paper, we consider the effect of adding a simple time filter to the Backward Euler scheme for the non-stationary coupled Stokes/Darcy model. The method is modular and requires only one additional line of code to be added, which improves the accuracy of the Backward Euler scheme from first to second order. We verify this conclusion from both theoretical analysis and numerical experiments. Finally, we propose that the BDF2 scheme can be improved to the third order if the time filter is added, which is demonstrated by numerical experiments. (C) 2019 IMACS. Published by Elsevier B.V.

[30]

Girault

, Raviart

P A

. Finite Element Approximation of the Navier-Stokes Equations. Berlin: Springer-Verlag, 1981

[31]

, Zhu

X H

Decoupled schemes for a non-stationary mixed Stokes-Darcy model

Mathematics of Computation, 2010, 79(270): 707-731

DOI:10.1090/S0025-5718-09-02302-3 URL [本文引用: 3]

[32]

, Lin

X L

, Chen

Z X

. Finite Volume Methods for the Incompressible Navier-Stokes Equations. Berlin: Springer-Verlag, 2021

[33]

李剑

. 不可压缩 Navier-Stokes 方程数值方法. 北京: 科学出版社, 2019

. Numerical Methods for the Incompressible Navier-Stokes Equations. Beijing: Science Press, 2019

[34]

李剑, 白云霄, 赵昕. 数学物理方程的现代数值方法. 北京: 科学出版社, 2022

, Bai

Y X

, Zhao

. Modern Numerical Methods for Mathematical Physics Equations. Beijing: Science Press, 2022

[35]

Qin

, Wang

Y S

, Li

A variable time step time filter algorithm for the geothermal system

SIAM Journal on Numerical Analysis, 2022, 60(5): 2781-2806

DOI:10.1137/21M1464828 URL

[36]

Cao

L L

, He

Y N

, Li

A parallel Robin-Robin domain decomposition method based on modified characteristic FEMs for the time-dependent dual-porosity-Navier-Stokes model with the Beavers-Joseph interface condition

Journal of Scientific Computing, 2022, 90(1): 1-34

DOI:10.1007/s10915-021-01681-y

[37]

Jiang

, Qiu

An efficient ensemble algorithm for numerical approximation of stochastic Stokes-Darcy equations

Computer Methods in Applied Mechanics and Engineering, 2019, 343: 249-275

DOI:10.1016/j.cma.2018.08.020 [本文引用: 1]

We propose and analyze an efficient ensemble algorithm for fast computation of multiple realizations of the stochastic Stokes-Darcy model with a random hydraulic conductivity tensor. The algorithm results in a common coefficient matrix for all realizations at each time step making solving the linear systems much less expensive while maintaining comparable accuracy to traditional methods that compute each realization separately. Moreover, it decouples the Stokes-Darcy system into two smaller sub-physics problems, which reduces the size of the linear systems and allows parallel computation of the two sub-physics problems. We prove the ensemble method is long time stable and first-order in time convergent under a time-step condition and two parameter conditions. Numerical examples are presented to support the theoretical results and illustrate the application of the algorithm. (C) 2018 Elsevier B.V.

[38]

, Hou

Y R

, Rong

A second-order artificial compression method for the evolutionary Stokes-Darcy system

Numerical Algorithms, 2020, 84(3): 1019-1048

DOI:10.1007/s11075-019-00791-x [本文引用: 1]

[39]

, Hou

Y R

Error estimates of second-order decoupled scheme for the evolutionary Stokes-Darcy system

Applied Numerical Mathematics, 2020, 154: 129-148