引言
磁共振成像(Magnetic Resonance Imaging,MRI)是一种卓越的非侵入性医学成像技术,可无损地获得生物体内不同对比度结构图像以及各种丰富的功能信息,如扩散、脑功能、代谢等,其在生物、医学等领域发挥着重要作用[1,2].超快MRI扫描技术能大幅缩短常规多次激发MRI方法的扫描时间,将几分钟缩短至毫秒量级.该技术不仅大幅提高了检测效率[3],而且由于其在毫秒级别尺度内生物体的宏观运动可以忽略不计,因此被广泛地应用于磁共振功能成像[4]、实时动态成像[5]和扩散张量成像[6]等领域.回波平面成像(Echo Planar Imaging,EPI)是最常见的超快MRI序列之一,该序列在单次射频脉冲激发后使用快速梯度切换以获取单个脉冲激发周期内的所有k空间编码信息,从而大大提升了其采样速度[7].由于EPI序列沿相位编码方向的带宽相对较低,使其对静磁场不均匀性较为敏感,因此EPI图像往往存在磁化率伪影或化学位移伪影[8],从而限制了其在高场磁共振系统上的进一步应用.值得注意的是,现有成熟的商用临床磁共振仪器可以利用并行成像技术缩短采样时间,从而在一定程度上克服磁场不均匀性的影响,然而在高场及超高场成像仪中,磁化率伪影仍是限制EPI的一个重要因素,而且在临床小动物实验中,由于磁体空间等限制,往往不能采用多通道的数据采集,因此如何实现无磁化率伪影的超快磁共振数据采集仍是磁共振领域的一个重要研究方向.
为克服EPI序列的磁化率及化学位移伪影问题,以色列威兹曼研究所的Lucio Frydman小组提出了一种新的超快磁共振序列:时空编码(Spatiotemporal Encoded,SPEN)MRI[9].该序列通过在相位编码维度引入线性扫频(Chirp)脉冲,并在梯度场的辅助下实现不同时刻对于不同位置上自旋的激发或重聚,从而实现对自旋的二次相位编码.在采样期间,SPEN通过梯度场作用不断实现二次相位顶点的移动,以实现整体空间自旋的解码[10].由于SPEN采用了与EPI相同的回波链数据采集方式,因此同样可以实现毫秒级的超快MRI,并且由于采用二次相位的空间编码方式,SPEN可以有效地提高相位编码维度的带宽,从而更好地抵抗场不均匀性及化学位移的影响[11].得益于二次相位编码的空间选择性,直接对SPEN采样信号进行求模操作,即可获得空间中不同位置的自旋密度(MRI图像).然而与EPI图像相比,直接求模值的SPEN图像空间分辨率较低.理论研究表明,在同等的采样情况下,SPEN模值图像的分辨率较EPI的结果下降了
SPEN的超分辨率重建算法与常规的图像超分辨率重建算法有所不同.SPEN的物理原理决定其超分辨率重建算法可以利用SPEN二次项相位顶点之间的冗余性来提高图像的空间分辨率[13].近年来,研究人员提出了多种SPEN超分辨率重建算法,如部分傅里叶法[14]和去卷积算法[15]等.部分傅里叶法利用SPEN采样信号的空间选择特性,仅考虑稳定相位点附近的采样信号,通过加权相位信息矩阵重建出超分辨率图像,该算法不需要进行迭代求解,因此重建速度较快.去卷积算法是一种灵活的超分辨率重建算法,该算法利用卷积性质,将空间编码采样信号转化为矩阵卷积的形式,进而利用反卷积算法重建出超分辨率图像,与原本的采样信号相比,矩阵卷积简化了SPEN采样信号的二次相位,使得采样信号更加平滑.同时,对平滑信号使用线性插值进行拟合扩充,提高了重建图像的数字分辨率.上述两种算法不需要迭代,可以快速重建出SPEN超分辨率图像,然而这两种算法需要对重建参数进行灵活调整从而得到较好的重建结果,在实际运用中,这两种算法往往比较繁琐,且重建结果受到采样点数和重建点数的限制.由于SPEN在相位编码维采用的带宽较大,从而使其对采样率有了更高的要求.在实际应用中,SPEN通常以欠采样的方式采集信号,使得其在相位编码维不满足奈奎斯特采样定律,导致其低分辨率图像中会产生伪影[13]. Chen等人提出的增强和边缘伪影去除法[16](Super-Resolved Enhancing and Edge Deghosting,SEED)通过探究SPEN超分辨率重建的质子密度分布与真实质子密度分布之间的关系,利用与混叠伪影相关的额外二次相位信息来构建先验信息,可以在不损失空间分辨率的情况下移除混叠伪影,使重建结果达到理论上的最优空间分辨率.然而该算法在重建过程中需要进行迭代求解,计算量较大、重建速度较慢.以上算法从二次相位调制的角度重建SPEN低分辨率图像,然而在图像域中伪影的产生往往难以解释,Zhong等人提出了一种从k空间视角去除混叠伪影并重建SPEN低分辨率图像的算法[17],该算法在k空间中以卷积矩阵的形式来描述SPEN采样信号的二次相位调制,并将SPEN超分辨率重建问题转化为反卷积问题,同时通过估计全采样和欠采样SPEN信号之间的差异来量化混叠伪影和边缘伪影,并采用压缩感知重建框架,使用非线性共轭梯度下降算法求解优化问题,最终重建出无伪影的SPEN超分辨率图像.
基于深度学习的重建算法在图像视觉及医学MRI影像领域取得了巨大的成功,其通过学习低分辨率图像到高分辨率图像之间的映射关系来进行重建[18,19].在MRI超分辨率重建方面,Bouter等人提出了一种基于深度学习的低场MRI超分辨率重建算法[20],该算法使用配对的低场低分辨率图像及高场高分辨率图像对卷积神经网络模型进行训练,然后在测试阶段输入低场低分辨率图像便可快速重建出清晰的高分辨率图像.Song等人提出了一种基于残差网络的脑部MRI超分辨率重建算法[21],该算法利用平均绝对误差损失的变体Charbonnier损失和梯度差分损失(Gradient Difference Loss)能够较好地处理异常值和锐化图像的特性,将这两种损失结合起来对网络模型进行训练,从而提高了训练模型的鲁棒性.
尽管卷积神经网络在图像恢复领域取得了广泛的应用,但其在提取图像像素长距离依赖关系方面表现出了一定的局限性.Transformer是一种通过注意力机制来学习全局依赖关系的神经网络模型[24],与卷积神经网络相比,Transformer可以更好的学习特征图的局部信息和长距离依赖关系,该模型已被广泛用于自然语言以及自然图像处理任务[25⇓-27].为了将Transformer应用于计算机视觉领域,谷歌团队于2020年提出了视觉Transformer[28](Vision Transformer,ViT),该方法将输入图像分成多个16×16的块,并把这些块通过全连接层压缩成高维向量后输入Transformer进行网络训练,与卷积神经网络相比,ViT在图像分类任务中取得了更为优秀的结果.为降低自注意力机制的计算复杂度,Liu等人提出了Swin Transformer架构[29],该架构用非重叠的窗口将特征图划分为数个大小相等的块,并在窗口内部进行局部自注意力计算,由于每个窗口中的图像块大小固定,因此自注意力机制的计算复杂度与输入图像大小呈线性关系,与二次关系相比大大减少了计算量.近年来,基于Transformer的方法在低级视觉任务中也逐渐兴起,常见的如IPT[30]、SwinIR[31]、Restormer[32]、Uformer[33]等模型在图像恢复中展现出了良好的性能,这些模型旨在从低质量的图像或视频中恢复出高分辨率的结果.
SPEN序列所采集得到的信号源于所有二次相位编码后自旋的贡献,因此原始的SPEN低分辨图像中各个像素之间存在一定的相关性[12].为此,本文提出了一种基于Transformer的SPEN超分辨率重建算法,该算法采用编码器-解码器的网络结构,在编码器和解码器中引入Transformer模型学习SPEN低分辨率图像特征的局部信息和长距离依赖关系.同时,引入Charbonnier损失和梯度差分损失分别作为主损失函数和辅助损失函数,提高网络模型的鲁棒性并增强超分辨率重建结果的纹理信息.实验结果表明,本文所提超分辨率重建算法可以在不增加额外采样点的情况下从SPEN低分辨率图像中重建出空间分辨率高、无混叠伪影的SPEN超分辨率图像.与现有基于U-Net的SPEN超分辨率重建算法和传统迭代超分辨率重建算法相比,本文提出的算法在临床数据集和临床前数据集上都取得了更好的重建效果.
1 实验部分
1.1 SPEN成像原理
图1
图1
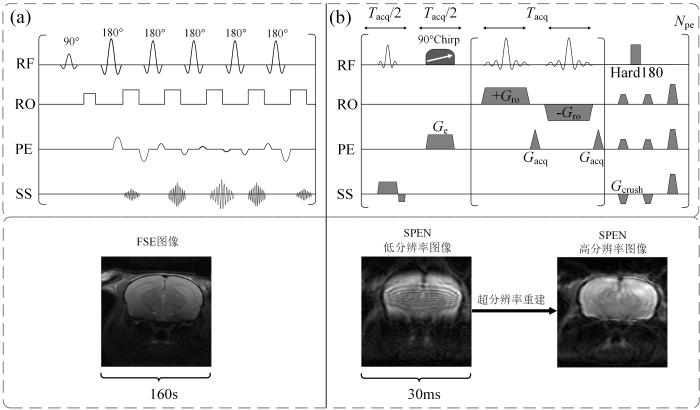
MRI中较为常用的多次扫描FSE序列与超快磁共振SPEN序列对比示意图. (a) FSE序列及其图像; (b) SPEN序列及其图像和超分辨率重建图
Fig. 1
The comparison of multiple scan FSE sequence and ultrafast magnetic resonance SPEN sequence commonly used in MRI. (a) FSE sequence and its image; (b) SPEN sequence and its image and super-resolution reconstruction image
与常规硬脉冲不同,Chirp脉冲随时间呈线性变化,该脉冲在激发作用期间的累计相位可表示为[13]:
其中
其中,
当Chirp脉冲的激发频率与自旋的共振频率一致时会产生共振,当激发结束时,自旋的累计相位可表示为:
其中,
其中,
其中,
与常规的MRI不同,SPEN成像采集的信号是一个包含二次相位调制的信号,因此不能直接采用傅里叶变换进行重建.从(5)式可以看出,SPEN序列采集的图像是空间中所有包含二次相位调制的自旋总和,由于二次相位除了在顶点处均处于快速变化的相位状态,因此只有顶点处的自旋对最后的SPEN图像有较大的贡献,可以直接采用求模值的操作获得图像.然而,这种求模值的操作忽略了顶点周围自旋的贡献,获得的SPEN图像类似于顶点处自旋和周围自旋卷积后的结果,因此分辨率较低,需要采用超分辨率算法重建恢复高分辨率图像.根据稳态相位近似原理,在二次相位驻点区域,自旋对采样信号强度的贡献大;在非二次相位驻点区域,自旋对采样信号强度的贡献较小.在驻点区域,信号模量可表示为:
其中Δy表示驻点的范围.
1.2 SPEN超分辨率重建原理
其中,N表示离散点的数量,2δ表示体素的宽度,
1.3 网络结构
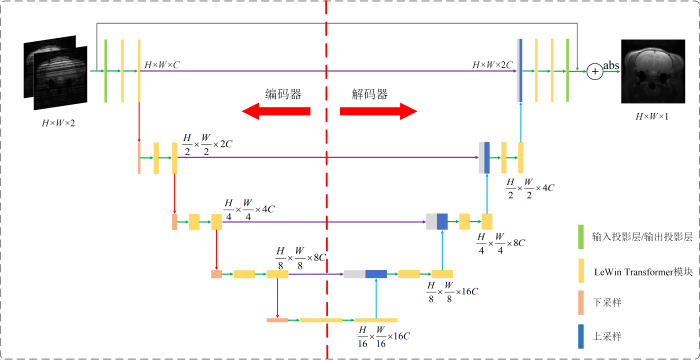
本文所提算法的网络框架如图2所示,该网络模型由编码器-解码器结构组成.编码器包含k个模块,每个模块由两个Transformer层和一个下采样层组成.编码器的第一个模块额外包含一个输入投影层(Input Projection)用于提取输入SPEN低分辨率图像的低级特征,并输出特征图
其中,Trans表示Transformer层,Downsampling表示下采样层.编码器-解码器结构的底部由两个Transformer层组成,用于捕获深层特征图像素间的全局依赖关系.同时,编码器和解码器的对应位置之间用跳跃连接进行通道拼接,跳跃连接操作可以使解码器在上采样时恢复更多的细节纹理特征.编码器的输出特征图
图2
图2
本文所提出的SPEN超分辨率重建网络结构图
Fig. 2
The SPEN super-resolution reconstruction network structure diagram proposed in this article
与编码器相同,解码器共由k个模块组成,每个模块包含两个Transformer层和一个上采样层,解码器的最后一个模块还额外包含一个输出投影层(Output Projection).其中输出投影层由卷积核大小为3×3,步长为1的卷积组成,用于将输出特征图恢复为残差图像
其中,Upsampling表示上采样层,cat表示跳跃连接.通过残差结构将残差图像R和输入图像I相加即可得到最终的图像,即Ioutput=I+R.
编码器和解码器采用了分层结构设计,其中浅层网络更加关注纹理等局部特征信息,深层网络随着感受野的增大更关注全局特征信息.因此分层特征图和窗口尺寸固定的设计使得Transformer可以捕获不同层次特征图的长距离依赖关系.
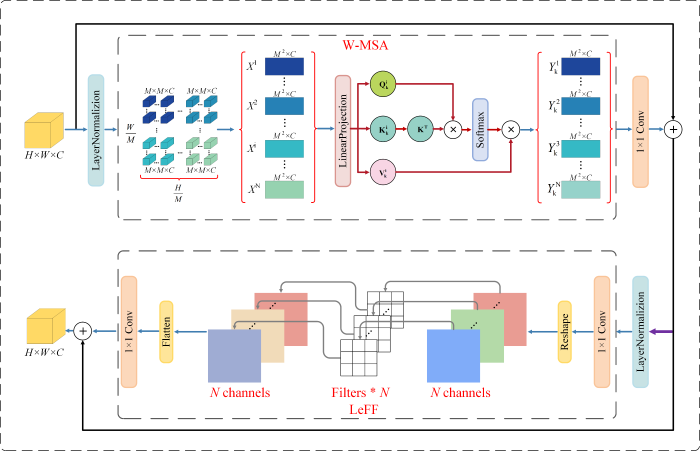
常规Transformer模型[35]中的自注意力机制需要计算输入特征图中所有元素之间的相关性,计算复杂度为O(H2W2C).这意味着,当输入特征图的尺寸增加时,Transformer模型的计算复杂度会呈平方级别增长,因此Transformer模型不适用于处理高空间分辨率的图像.此外,超分辨率重建主要利用相邻像素之间的相关性,距离越近的像素其关联层度越高,而Transformer在捕获局部上下文信息方面表现出了一定的局限性[36,37].为了更好地捕获输入特征图的局部上下文信息并降低自注意力的计算成本,本文引入局部增强窗口(Locally-enhanced Window,LeWin)Transformer模块[33].如图3所示,LeWin Transformer主要由基于窗口的多头自注意力(Window-based Multihead Self-Attention,W-MSA)和局部增强前馈(Locally-enhanced Feed-Forward,LeFF)网络组成.
图3
图3
本文采用的LeWin Transformer模块示意图,主要包括W-MSA和LeFF两部分
Fig. 3
The schematic diagram of the LeWin Transformer module used in this article mainly includes two parts: W-MSA and LeFF
W-MSA的计算流程如下,输入特征图
其中,SoftMax为激活函数,用于将向量转换为概率分布,
W-MSA通过计算特征图中元素之间的依赖关系提高了模型捕获长距离依赖关系的能力,然而W-MSA没有充分考虑相邻元素之间的局部相关性.与自注意力层相比,前馈神经网络主要用于对自注意力层的输出进行进一步的变换以增强模型的非线性表达能力,然而,前馈神经网络层没有考虑元素之间的空间关系.在视觉恢复任务中,卷积可以有效提取相邻像素之间的局部信息,传统的卷积使用大小固定的卷积核对输入特征图的每个位置进行卷积计算,因而参数量较大.与传统的卷积不同,深度卷积的每个卷积核只对特征图的一个通道进行处理,从而减少了卷积运算的参数量,更利于深层网络的计算.LeFF模块通过引入深度卷积以促进空间维度中相邻元素之间的局部上下文信息.LeFF的具体计算流程为:首先将输入特征图通过线性投影层以增加特征维度,然后对输入特征图使用深度卷积捕获局部上下文信息,随后将特征图再次输入线性投影层以匹配输入特征图通道.
与Uformer不同,本文所提网络结构更轻量,同时本文根据SPEN输入数据的特点设计特征通道数以及网络结构中每层使用Transformer模块的数量.此外,本文利用Charbonnier损失和梯度差分损失能较好的处理异常值并保留图像的纹理和细节特征的特点,将这两种损失函数结合起来对网络进行训练.在讨论以及补充信息中,本文探讨了不同特征通道数、不同Transformer模块的数量、以及损失函数不同权重对训练结果的影响.
训练网络的损失函数包括Charbonnier损失和梯度差分损失两种.其中Charbonnier损失是图像处理中常用的一种损失,该损失可以较好的处理异常值,其计算过程如下[21]:
其中,I表示网络输出,
其中,i、j分别表示图像的行和列,
其中,λ表示超参数,用于调节两种损失的权重.
1.4 评价指标
本文使用峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)和结构相似性(Structure Similarity Index Measurement,SSIM)作为仿真数据集的评价指标.PSNR用来衡量图像质量的好坏,PSNR越高说明图像质量越好;SSIM用来比较真实图像与重建图像之间的相似度,范围在0到1之间,SSIM越接近1说明重建图像与真实图像之间的差距越小.PSNR和SSIM的计算式如下:
其中,mse表示均方误差,x为真值,y为重建之后的图像,μ表示图像像素的均值,σ表示图像像素之间的方差,σxy表示x和y的协方差,c1和c2表示使分母避免为0的常数项.
1.5 数据集与实验参数
本文训练数据集包括临床数据集以及临床前数据集两种.其中临床数据集由HCP网站[38]中公开的人脑结构图像作为人脑仿真数据的参考图像,并通过脉冲序列仿真生成SPEN低分辨率图像;临床前数据集由武汉磁共振中心Bruker Biospec 7T小动物成像仪上分别使用FSE序列、单扫描EPI序列和单扫描SPEN序列对活体大鼠脑袋进行数据采集获取.其中FSE图像作为大鼠脑仿真数据的参考图像,并通过SPEN脉冲序列仿真生成的SPEN低分辨率图像用于临床前数据的超分辨重建网络训练;实际采集的单扫描SPEN低分辨率图像用于作为测试数据集;单扫描EPI图像作为与SPEN数据的对比图像.在网络训练阶段,本文分别使用人脑结构图像或者大鼠脑FSE图像作为标签数据、其对应的脉冲序列仿真SPEN低分辨率图像作为网络输入进行有监督训练.为验证Transformer超分辨率重建算法在实采数据上的重建效果并测试其泛化能力,本文采集了小鼠脑临床前数据进行了测试,并与FSE和EPI序列进行了对比.
所有动物实验均按照国家卫生研究院动物护理指南进行,并且实验程序经过中国科学院精密测量科学技术创新研究院动物伦理委员会批准(APM2022A).在大鼠以及小鼠磁共振成像实验中,通过使用异氟烷与氧气混合以麻醉大鼠以及小鼠(4.0%~5.0%用于刺激诱导,0.5%~1.0%用于维持成像).在扫描期间,持续监测麻醉状态下大鼠以及小鼠的呼吸频率(30~50次/min),并通过37 ℃的水循环维持大鼠以及小鼠体温.FSE序列的采集参数如下:重复时间(TR)为2 500 ms,有效TE为32 ms,回波数为8,层厚为1 mm,视野大小为35 mm×35 mm(大鼠)/20 mm×20 mm(小鼠),采集矩阵为256×256;单扫描EPI序列的采集参数为:TR为2 500 ms,TE为32 ms,层厚为1 mm,带宽为500 kHz,视野大小为35 mm×35 mm(大鼠)/20 mm×20 mm(小鼠),采集矩阵为96×96;单扫描SPEN序列的采集参数与单扫描EPI序列上述参数相同,SPEN序列的R值为120.仿真生成的SPEN超分辨率编码系数矩阵的参数与单扫描SPEN序列的采集参数保持一致.
本文提出的网络算法基于Pytorch搭建,采用AdamW优化器更新网络参数,其超参数为β1=0.9,β2=0.999,ε=10-8.网络训练的批数据大小设置为4,初始学习率设置为0.000 2,并使用Warm-up策略对学习率进行动态调整.λ的值设置为0.1,以保持各项损失函数对总函数的影响处于同一水平.实验用的硬件配置为NVIDIA GeForce GTX 2080,内存为128 GB,操作系统为Ubuntu 20.04.
2 结果与讨论
2.1 仿真数据结果分析
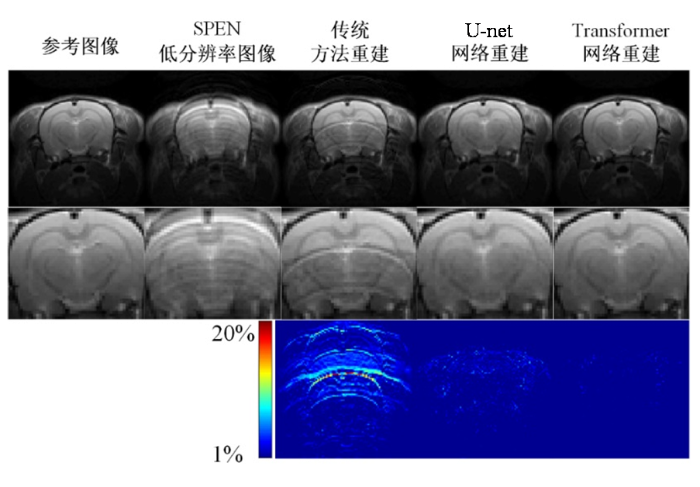
图4展示了各超分辨率重建算法在大鼠脑仿真数据上的重建结果.第一行从左到右分别对应参考图像、未重建的SPEN低分辨率图像、传统迭代超分辨率重建算法、U-Net超分辨率重建算法以及Transformer超分辨率重建算法的重建结果,第二行分别为各个图像的局部区域放大图,第三行分别为各算法重建结果与参考图像之间的误差图.从重建结果图上看,Transformer重建算法的重建结果空间分辨率高、无混叠伪影,且重建结果纹理清晰,而传统迭代重建算法的重建结果伴有一定程度的混叠伪影,大大影响了视觉效果.从局部区域放大图上来看,U-Net重建算法在局部放大图中仍残留混叠伪影,且重建结果的空间分辨率以及清晰度均低于Transformer重建算法.从误差图上来看,Transformer重建算法与参考图像之间的误差值整体最小,U-Net重建算法与参考图像之间有一定的误差,而传统重建算法与参考图像之间误差较大,从而说明Transformer重建算法的重建结果与参考图像最接近,重建效果最好.
图4
图4
各种SPEN超分辨率算法在大鼠脑仿真数据集重建结果对比
Fig. 4
The comparison of reconstruction results with different SPEN super-resolution algorithms on the simulated Rat brain dataset
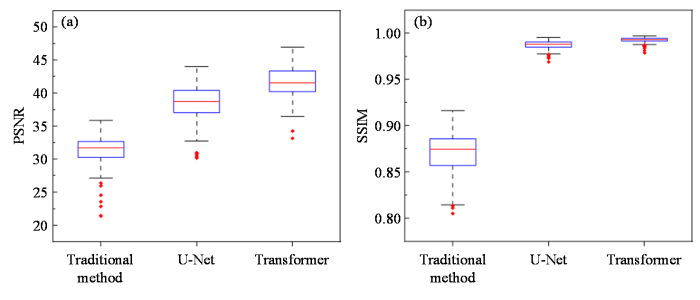
图5展示了各超分辨率重建算法在大鼠脑仿真数据上的统计定量分析结果.图5(a)和图5(b)分别为各个算法在大鼠脑仿真测试数据集上的PSNR和SSIM箱型图,箱型图中箱体的水平线表示中位数,箱体的上下限分别表示数据的上四分位数和下四分位数,数据的最大值和最小值通过须线和箱体相连.箱型图可以直观地反映数据的分布情况和集中趋势.从PSNR和SSIM箱型图上来看,Transformer重建算法在测试集上的评价指标结果整体水平高于U-Net重建算法以及传统重建算法,并且Transformer重建算法重建结果的SSIM数值分布较为集中、离散程度较小,而传统重建算法的SSIM箱型图离散程度较大,说明该算法可能引入了不同程度的伪影,对不同数据的重建结果有一定差别.此外,我们又对鼠脑仿真测试数据集中PSNR数值的一致性进行了分析,结果显示Transformer重建算法和U-Net重建算法、传统迭代重建算法之间的散点大多数都分布在95%一致性界限内,三种算法之间的PSNR数值具有良好的一致性水平,详情可见附件材料图S1.
图5
图5
各种SPEN超分辨率算法在大鼠脑仿真数据集上的统计重建指标对比. (a) PSNR;(b) SSIM
Fig. 5
The comparison of statistical indicators with different SPEN super-resolution algorithms on the simulated rat brain dataset. (a) PSNR; (b) SSIM
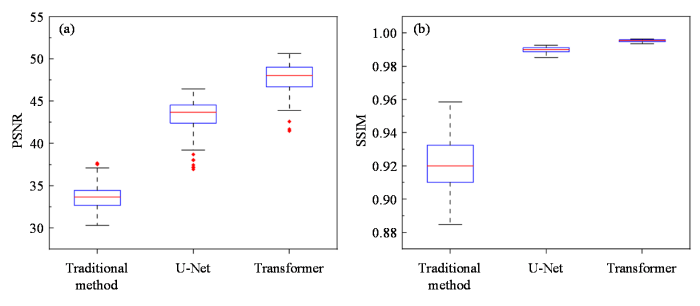
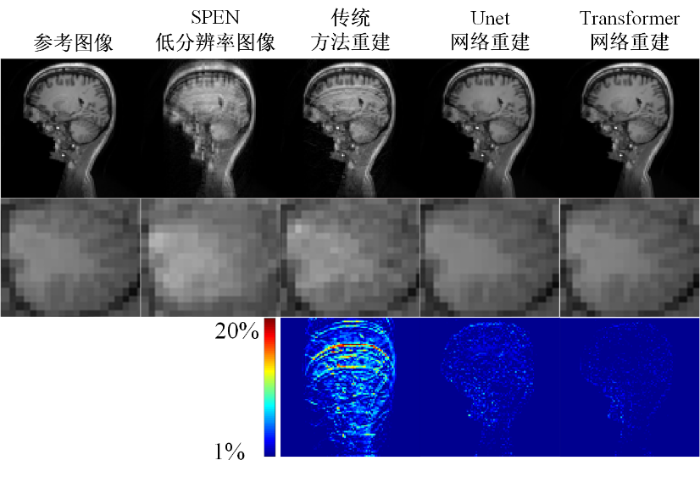
本文还在人脑仿真数据上进行了超分辨率重建和结果分析,以验证Transformer重建算法在不同数据集上的适用性.图6展示了各超分辨率重建算法在人脑仿真数据集上的重建结果,第一行从左到右分别对应参考图像、未重建的SPEN低分辨率图像、传统迭代超分辨率重建算法、U-Net超分辨率重建算法以及Transformer超分辨率重建算法的重建结果,第二行分别为各个图像的局部区域放大图,第三行分别为各算法重建结果与参考图像之间的误差图.与大鼠脑仿真数据集上的实验结论一致,较传统迭代算法和U-Net超分辨率重建算法相比,Transformer重建算法在人脑仿真数据上仍能重建出空间分辨率高且误差更小的超分辨率图像.
图6
图6
各种SPEN超分辨率算法在HCP人脑仿真数据集重建结果对比
Fig.6
The comparison of reconstruction results with different SPEN super-resolution algorithms
on the simulated HCP T1weighted dataset
图7
图7
各种SPEN超分辨率重建算法在HCP人脑仿真数据集上的统计指标对比. (a) PSNR;(b) SSIM
Fig. 7
The comparison of statistical indicators with different SPEN super-resolution algorithms on the simulated HCP T1 weighted dataset. (a) PSNR; (b) SSIM
2.2 实采数据结果分析
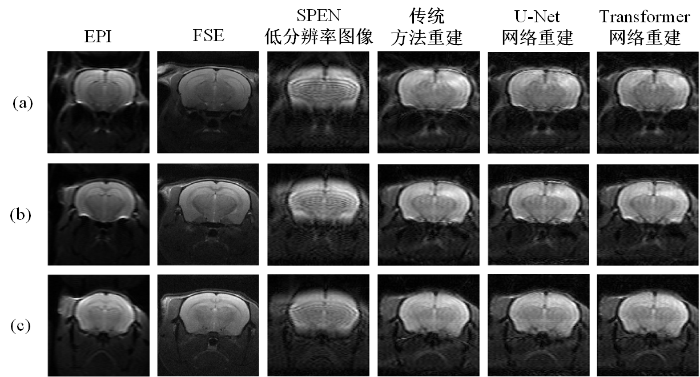
图8对比展示了各个算法在临床前小鼠脑数据上的重建结果,并与EPI、FSE序列采集结果进行了对比.图中从左到右依次为EPI图像、FSE图像、SPEN低分辨率图像、传统迭代超分辨率重建算法、U-Net超分辨率重建算法以及Transformer超分辨率重建算法的重建结果,第一、二、三行分别表示实采数据集中随机选取的不同测试数据.从图中可以看出,由于受到磁场不均匀性和化学位移的影响,EPI图像表现出一定程度的几何失真,SPEN图像较好地抵抗了磁场不均匀性和化学位移的影响,然而未重建的SPEN图像空间分辨率较低,无法呈现小鼠脑细节.从重建结果上来看,传统迭代重建算法的重建结果残留一定的伪影,与Transformer重建算法相比,U-Net超分辨率重建算法的重建结果分辨率略低,而Transformer重建算法的结果较好地去除了混叠伪影、重建图像纹理清晰.
图8
图8
各种SPEN超分辨率重建算法在真实活体小鼠脑数据上的重建结果对比
Fig. 8
The comparison of reconstruction results with different SPEN super-resolution algorithms on real in vivo mice dataset acquired with Bruker
2.3 讨论
本文提出了一种基于Transformer的时空编码超分辨率重建算法,该算法采用Charbonnier损失和梯度差分损失对网络进行训练.本文在临床数据集和临床前数据集上对Transformer重建算法进行了定性和定量分析,并与现有U-Net重建算法及传统迭代重建算法进行了对比.从重建结果上看,Transformer重建算法在临床数据集和临床前数据集上均展现出了优秀的性能.
由于Transformer重建算法在训练时需要配对的训练数据,而真实的实验环境往往受到各种因素的干扰,难以获得配对的参考图像,因此本文基于SPEN MRI原理,采用仿真数据制作方法生成SPEN图像以获取训练样本.
Transformer重建算法的重建结果会受到损失函数、输入特征通道数、Transformer层数等因素的影响,为了探讨各种因素对重建结果的影响,本文分别设置不同的超参数对网络进行消融实验并计算评价指标以分析结果.本文训练参数默认设置为输入特征通道数C=24、Transformer层数T=2且使用混合损失函数,在进行消融实验时除实验参数外其他设置保持不变.如表1所示,使用Charbonnier损失和梯度差分损失混合训练的网络重建结果在评价指标上优于不使用梯度差分损失的重建结果,说明梯度差分损失可以增强重建性能,不同损失函数的网络重建结果详情可见附件材料图S3.此外,随着C的增加,网络重建结果的PSNR和SSIM有一定提升,但是计算量和模型参数也随之提升,为了保持网络模型具有较好的重建能力同时具有较小的模型计算量,本文C设置为24,不同C值的网络重建结果详情可见附件材料图S4.其次,增加Transformer层数T可以提高模型的重建效果,但是其对应的计算量和模型参数也随之提升.当T增加到2时,模型的重建效果表现出较好的水平,继续增大T时网络重建结果的PSNR和SSIM提升较小,但与之对应的模型参数量迅速增加.因此,为了保持网络模型具有较好的重建能力同时具有较小的模型计算量,本文T设置为2,不同T值的网络重建结果详情可见附件材料图S5.
表1 不同因素影响下的消融实验
Table 1
| 方法 | PSNR/dB | SSIM | FLOPS | 模型参数/MB |
|---|---|---|---|---|
| 传统迭代重建 | 31.08 | 0.8928 | - | - |
| U-Net重建 | 38.58 | 0.9812 | 5.48 | 5.3 |
| Transformer (C=12) | 38.85 | 0.9801 | 4.42 | 3.0 |
| Transformer (C=24) | 45.22 | 0.9928 | 16.14 | 11.6 |
| Transformer (C=48) | 53.31 | 0.9983 | 61.48 | 46.2 |
| Transformer (T=1) | 42.34 | 0.9877 | 8.71 | 6.8 |
| Transformer (T=2) | 45.22 | 0.9928 | 16.14 | 11.6 |
| Transformer (T=3) | 45.41 | 0.9928 | 23.57 | 16.4 |
| Transformer (Without GDL) | 42.83 | 0.9901 | 16.14 | 11.6 |
| Transformer (With GDL) | 45.22 | 0.9928 | 16.14 | 11.6 |
注:FLOPS表示浮点运算次数.
本研究也存在一定的局限性和不足.首先,本文提出的算法在使用同一类型的数据训练并测试时可以得到良好的测试结果,然而在保持其他参数不变的情况下,当训练集和测试集的数据类型不一致时,测试结果就会受到影响,说明本文提出方法在不同类型数据集上的泛化能力还有待提高.其次,网络重建的结果与训练样本的仿真参数密切相关.只有当仿真实验参数与真实采样实验参数基本一致时才能重建出较好的高分辨率图像.由于SPEN采集方法的特殊性,高分辨率的SPEN图像只能通过非线性的重建算法获取,本文提出了一种基于Transformer网络的SPEN高分辨率重建算法,其主要包括三个步骤:(1)仿真获取训练数据,采用在高分辨率的MRI图像基础上使用SPEN序列仿真的方式,获取原始的低分辨率SPEN图像;(2)Transformer网络训练,使用仿真数据训练网络,学习从原始SPEN低分辨率图像到SPEN超分辨率MRI图像的映射关系;(3)真实SPEN低分辨率图像的重建,利用训练好的网络实现SPEN低分辨率图像到超分辨率图像之间的重建.本文提出的超分辨率重建算法相比于现有的非线性重建算法重建结果有提升,然而在实际的活体数据测试中仍存在一定的模糊,这是因为在仿真过程中,本文没有考虑实验磁场均匀性等影响,所以仿真算法与实际采样之间略有区别.在后期的研究方向中可以尝试泛化能力更强的网络,或者无监督网络模型,从而提升算法的实际泛化能力.
3 结论
本文提出了一种基于Transformer的时空编码MRI超分辨率重建算法,该算法由编码器-解码器结构组成,在编码器和解码器中引入Transformer模块代替卷积层以提取特征图的局部上下文信息和长距离依赖关系.在临床数据集和临床前数据集上的实验结果表明,与现有基于U-Net的超分辨率重建算法和传统迭代重建算法相比,本文所提算法重建图像空间分辨率更高、纹理细节清晰,同时在PSNR和SSIM方面均有明显的提升.
利益冲突
无
附件材料
附件材料(可在《波谱学杂志》官网
图S1 各种SPEN超分辨率算法在大鼠脑仿真数据集上的Bland-Altman图
图S2 各种SPEN超分辨率算法在HCP人脑仿真数据集上的Bland-Altman图
图S3 不同损失函数的消融实验
图S4 不同特征通道数的消融实验
图S5 不同Transformer层数的消融实验
参考文献
A modified reptile search algorithm for global optimization and image segmentation: Case study brain MRI images
[J].
2D versus 3D MRI of osteoarthritis in clinical practice and research
[J].
DOI:10.1007/s00256-023-04309-4
PMID:36907953
[本文引用: 1]

Accurately detecting and characterizing articular cartilage defects is critical in assessing patients with osteoarthritis. While radiography is the first-line imaging modality, magnetic resonance imaging (MRI) is the most accurate for the noninvasive assessment of articular cartilage. Multiple semiquantitative grading systems for cartilage lesions in MRI were developed. The Outerbridge and modified Noyes grading systems are commonly used in clinical practice and for research. Other useful grading systems were developed for research, many of which are joint-specific. Both two-dimensional (2D) and three-dimensional (3D) pulse sequences are used to assess cartilage morphology and biochemical composition. MRI techniques for morphological assessment of articular cartilage can be categorized into 2D and 3D FSE/TSE spin-echo and gradient-recalled echo sequences. T2 mapping is most commonly used to qualitatively assess articular cartilage microstructural composition and integrity, extracellular matrix components, and water content. Quantitative techniques may be able to label articular cartilage alterations before morphological defects are visible. Accurate detection and characterization of shallow low-grade partial and small articular cartilage defects are the most challenging for any technique, but where high spatial resolution 3D MRI techniques perform best. This review article provides a practical overview of commonly used 2D and 3D MRI techniques for articular cartilage assessments in osteoarthritis.© 2023. The Author(s), under exclusive licence to International Skeletal Society (ISS).
Ultrafast imaging: principles, pitfalls, solutions, and applications
[J].
DOI:10.1002/jmri.22239
PMID:20677249
[本文引用: 1]

Ultrafast MRI refers to efficient scan techniques that use a high percentage of the scan time for data acquisition. Often, they are used to achieve short scan duration ranging from sub-second to several seconds. Alternatively, they may form basic components of longer scans that may be more robust or have higher image quality. Several important applications use ultrafast imaging, including real-time dynamic imaging, myocardial perfusion imaging, high-resolution coronary imaging, functional neuroimaging, diffusion imaging, and whole-body scanning. Over the years, echo-planar imaging (EPI) and spiral imaging have been the main ultrafast techniques, and they will be the focus of the review. In practice, there are important challenges with these techniques, as it is easy to push imaging speed too far, resulting in images of a nondiagnostic quality. Thus, it is important to understand and balance the trade-off between speed and image quality. The purpose of this review is to describe how ultrafast imaging works, the potential pitfalls, current solutions to overcome the challenges, and the key applications.2010 Wiley-Liss, Inc.
Neuroplasticity-driven timing modulations revealed by ultrafast functional magnetic resonance imaging
[J].
Real-time magnetic resonance imaging in pediatric radiology—new approach to movement and moving children
[J].
How to optimize breast MRI protocol? The value of combined analysis of ultrafast and diffusion-weighted MRI sequences
[J].
Highly efficient MRI through multi-shot echo planar imaging
[C]//
An unsupervised deep learning technique for susceptibility artifact correction in reversed phase-encoding EPI images
[J].
DOI:S0730-725X(19)30732-5
PMID:32407764
[本文引用: 1]

Echo planar imaging (EPI) is a fast and non-invasive magnetic resonance imaging technique that supports data acquisition at high spatial and temporal resolutions. However, susceptibility artifacts, which cause the misalignment to the underlying structural image, are unavoidable distortions in EPI. Traditional susceptibility artifact correction (SAC) methods estimate the displacement field by optimizing an objective function that involves one or more pairs of reversed phase-encoding (PE) images. The estimated displacement field is then used to unwarp the distorted images and produce the corrected images. Since this conventional approach is time-consuming, we propose an end-to-end deep learning technique, named S-Net, to correct the susceptibility artifacts the reversed-PE image pair. The proposed S-Net consists of two components: (i) a convolutional neural network to map a reversed-PE image pair to the displacement field; and (ii) a spatial transform unit to unwarp the input images and produce the corrected images. The S-Net is trained using a set of reversed-PE image pairs and an unsupervised loss function, without ground-truth data. For a new image pair of reversed-PE images, the displacement field and corrected images are obtained simultaneously by evaluating the trained S-Net directly. Evaluations on three different datasets demonstrate that S-Net can correct the susceptibility artifacts in the reversed-PE images. Compared with two state-of-the-art SAC methods (TOPUP and TISAC), the proposed S-Net runs significantly faster: 20 times faster than TISAC and 369 times faster than TOPUP, while achieving a similar correction accuracy. Consequently, S-Net accelerates the medical image processing pipelines and makes the real-time correction for MRI scanners feasible. Our proposed technique also opens up a new direction in learning-based SAC.Copyright © 2020 Elsevier Inc. All rights reserved.
Spatially encoded NMR and the acquisition of 2D magnetic resonance images within a single scan
[J].An approach that enables the acquisition of multidimensional NMR spectra within a single scan has been recently proposed and demonstrated. The present paper explores the applicability of such ultrafast acquisition schemes toward the collection of two-dimensional magnetic resonance imaging (2D MRI) data. It is shown that ideas enabling the application of these spatially encoded schemes within a spectroscopic setting, can be extended in a straightforward manner to pure imaging. Furthermore, the reliance of the original scheme on a spatial encoding and subsequent decoding of the evolution frequencies endows imaging applications with a greater simplicity and flexibility than their spectroscopic counterparts. The new methodology also offers the possibility of implementing the single-scan acquisition of 2D MRI images using sinusoidal gradients, without having to resort to subsequent interpolation procedures or non-linear sampling of the data. Theoretical derivations on the operational principles and imaging characteristics of a number of sequences based on these ideas are derived, and experimentally validated with a series of 2D MRI results collected on a variety of model phantom samples.
Spatiotemporally encoded nuclear magnetic resonance and its applications
[J].
时空编码核磁共振方法及其应用
[J].
Spatial encoding and the single-scan acquisition of high definition MR images in inhomogeneous fields
[J].We have recently proposed a protocol for retrieving multidimensional magnetic resonance spectra and images within a single scan, based on a spatial encoding of the spin interactions. The spatial selectivity of this encoding process also opens up new possibilities for compensating magnetic field inhomogeneities; not by demanding extreme uniformities from the B(0) fields, but by compensating for their effects at an excitation and/or refocusing level. This potential is hereby discussed and demonstrated in connection with the single-scan acquisition of high-definition multidimensional images. It is shown that in combination with time-dependent gradient and radiofrequency manipulations, the new compensation approach can be used to counteract substantial field inhomogenities at either global or local levels over relatively long periods of time. The new compensation scheme could find uses in areas where heterogeneities in magnetic fields present serious obstacles, including rapid studies in regions near tissue/air interfaces. The principles of the B(0) compensation method are reviewed for one- and higher-dimensional cases, and experimentally demonstrated on a series of 1D and 2D single-scan MRI experiments on simple phantoms.
Single-scan multidimensional magnetic resonance
[J].
Super-resolved spatially encoded single-scan 2D MRI
[J].
Partial Fourier transform reconstruction for single-shot MRI with linear frequency-swept excitation
[J].
DOI:10.1002/mrm.24366
PMID:22706702
[本文引用: 3]

A novel image encoding approach based on linear frequency-swept excitation has been recently proposed to overcome artifacts induced by various field perturbations in single-shot echo planar imaging. In this article, we develop a new super-resolved reconstruction method for it using the concepts of local k-space and partial Fourier transform. This method is superior to the originally developed conjugate gradient algorithm in convenience, image quality, and stability of solution. Reduced field-of-view is applied to the phase encoding direction to further enhance the spatial resolution and field perturbation immunity of the image obtained. Effectiveness of this new combined reconstruction method is demonstrated with a series of experiments on biological samples. Two single-shot sequences with different encoding features are tested. The results show that this reconstruction method maintains excellent field perturbation immunity and improves fidelity of the images. In vivo experiments on rat indicate that this solution is favorable for ultrafast imaging applications in which severe susceptibility heterogeneities around the tissue-air or tissue-bone interfaces, motion and oblique plane effects usually compromise the echo planar imaging image quality.Copyright © 2012 Wiley Periodicals, Inc.
An efficient de-convolution reconstruction method for spatiotemporal-encoding single-scan 2D MRI
[J].
DOI:10.1016/j.jmr.2012.12.020
PMID:23433507
[本文引用: 1]

Spatiotemporal-encoding single-scan MRI method is relatively insensitive to field inhomogeneity compared to EPI method. Conjugate gradient (CG) method has been used to reconstruct super-resolved images from the original blurred ones based on coarse magnitude-calculation. In this article, a new de-convolution reconstruction method is proposed. Through removing the quadratic phase modulation from the signal acquired with spatiotemporal-encoding MRI, the signal can be described as a convolution of desired super-resolved image and a point spread function. The de-convolution method proposed herein not only is simpler than the CG method, but also provides super-resolved images with better quality. This new reconstruction method may make the spatiotemporal-encoding 2D MRI technique more valuable for clinic applications.Copyright © 2013 Elsevier Inc. All rights reserved.
Super-resolved enhancing and edge deghosting (SEED) for spatiotemporally encoded single-shot MRI
[J].
DOI:10.1016/j.media.2015.03.004
PMID:25910683
[本文引用: 1]

Spatiotemporally encoded (SPEN) single-shot MRI is an ultrafast MRI technique proposed recently, which utilizes quadratic rather than linear phase profile to extract the spatial information. Compared to the echo planar imaging (EPI), this technique has great advantages in resisting field inhomogeneity and chemical shift effects. Super-resolved (SR) reconstruction is adopted to compensate the inherent low resolution of SPEN images. Due to insufficient sampling rate, the SR image is challenged by aliasing artifacts and edge ghosts. The existing SR algorithms always compromise in spatial resolution to suppress these undesirable artifacts. In this paper, we proposed a novel SR algorithm termed super-resolved enhancing and edge deghosting (SEED). Different from artifacts suppression methods, our algorithm aims at exploiting the relationship between aliasing artifacts and real signal. Based on this relationship, the aliasing artifacts can be eliminated without spatial resolution loss. According to the trait of edge ghosts, finite differences and high-pass filter are employed to extract the prior knowledge of edge ghosts. By combining the prior knowledge with compressed sensing, our algorithm can efficiently reduce the edge ghosts. The robustness of SEED is demonstrated by experiments under various situations. The results indicate that the SEED can provide better spatial resolution compared to state-of-the-art SR reconstruction algorithms in SPEN MRI. Theoretical analysis and experimental results also show that the SR images reconstructed by SEED have better spatial resolution than the images obtained with conventional k-space encoding methods under similar experimental condition. Copyright © 2015 Elsevier B.V. All rights reserved.
Understanding aliasing effects and their removal in SPEN MRI: A k-space perspective
[J].
DOI:10.1002/mrm.29638
PMID:36961093
[本文引用: 1]

To characterize the mechanism of formation and the removal of aliasing artifacts and edge ghosts in spatiotemporally encoded (SPEN) MRI within a k-space theoretical framework.SPEN's quadratic phase modulation can be described in k-space by a convolution matrix whose coefficients derive from Fourier relations. This k-space model allows us to pose SPEN's reconstruction as a deconvolution process from which aliasing and edge ghost artifacts can be quantified by estimating the difference between a full sampling and reconstructions resulting from undersampled SPEN data.Aliasing artifacts in SPEN MRI reconstructions can be traced to image contributions corresponding to high-frequency k-space signals. The k-space picture provides the spatial displacements, phase offsets, and linear amplitude modulations associated to these artifacts, as well as routes to removing these from the reconstruction results. These new ways to estimate the artifact priors were applied to reduce SPEN reconstruction artifacts on simulated, phantom, and human brain MRI data.A k-space description of SPEN's reconstruction helps to better understand the signal characteristics of this MRI technique, and to improve the quality of its resulting images.© 2023 International Society for Magnetic Resonance in Medicine.
Magnetic resonance image reconstruction of multi-scale residual unet fused with attention mechanism
[J].
融合注意力机制的多尺度残差Unet的磁共振图像重建
[J].
Magnetic resonance R2* parameter mapping of liver based on self-supervised deep neural network
[J].
基于自监督网络的肝脏磁共振R2*参数图像重建
[J].
Deep learning-based single image super-resolution for low-field MR brain images
[J].
DOI:10.1038/s41598-022-10298-6
PMID:35430586
[本文引用: 1]

Low-field MRI scanners are significantly less expensive than their high-field counterparts, which gives them the potential to make MRI technology more accessible all around the world. In general, images acquired using low-field MRI scanners tend to be of a relatively low resolution, as signal-to-noise ratios are lower. The aim of this work is to improve the resolution of these images. To this end, we present a deep learning-based approach to transform low-resolution low-field MR images into high-resolution ones. A convolutional neural network was trained to carry out single image super-resolution reconstruction using pairs of noisy low-resolution images and their noise-free high-resolution counterparts, which were obtained from the publicly available NYU fastMRI database. This network was subsequently applied to noisy images acquired using a low-field MRI scanner. The trained convolutional network yielded sharp super-resolution images in which most of the high-frequency components were recovered. In conclusion, we showed that a deep learning-based approach has great potential when it comes to increasing the resolution of low-field MR images.© 2022. The Author(s).
Deep robust residual network for super-resolution of 2D fetal brain MRI
[J].
DOI:10.1038/s41598-021-03979-1
PMID:35013383
[本文引用: 3]

Spatial resolution is a key factor of quantitatively evaluating the quality of magnetic resonance imagery (MRI). Super-resolution (SR) approaches can improve its spatial resolution by reconstructing high-resolution (HR) images from low-resolution (LR) ones to meet clinical and scientific requirements. To increase the quality of brain MRI, we study a robust residual-learning SR network (RRLSRN) to generate a sharp HR brain image from an LR input. Due to the Charbonnier loss can handle outliers well, and Gradient Difference Loss (GDL) can sharpen an image, we combined the Charbonnier loss and GDL to improve the robustness of the model and enhance the texture information of SR results. Two MRI datasets of adult brain, Kirby 21 and NAMIC, were used to train and verify the effectiveness of our model. To further verify the generalizability and robustness of the proposed model, we collected eight clinical fetal brain MRI 2D data for evaluation. The experimental results have shown that the proposed deep residual-learning network achieved superior performance and high efficiency over other compared methods.© 2022. The Author(s).
Super-resolved reconstruction method for spatiotemporally encoded magnetic resonance imaging based on deep neural network
>[J].
基于深度神经网络的时空编码磁共振成像超分辨率重建方法
[J].
Ultrafast water-fat separation using deep learning-based single-shot MRI
[J].
Transformer architecture and attention mechanisms in genome data analysis: a comprehensive review
[J].
End-to-end transformer-based models in textual-based NLP
[J].
Application of visual transformer in renal image analysis
[J].
DOI:10.1186/s12938-024-01209-z
PMID:38439100
[本文引用: 1]

Deep Self-Attention Network (Transformer) is an encoder-decoder architectural model that excels in establishing long-distance dependencies and is first applied in natural language processing. Due to its complementary nature with the inductive bias of convolutional neural network (CNN), Transformer has been gradually applied to medical image processing, including kidney image processing. It has become a hot research topic in recent years. To further explore new ideas and directions in the field of renal image processing, this paper outlines the characteristics of the Transformer network model and summarizes the application of the Transformer-based model in renal image segmentation, classification, detection, electronic medical records, and decision-making systems, and compared with CNN-based renal image processing algorithm, analyzing the advantages and disadvantages of this technique in renal image processing. In addition, this paper gives an outlook on the development trend of Transformer in renal image processing, which provides a valuable reference for a lot of renal image analysis.© 2024. The Author(s).
SwinT-SRNet: Swin transformer with image super-resolution reconstruction network for pollen images classification
[J].
An image is worth 16x16 words: Transformers for image recognition at scale
[C]//
Swin transformer: hierarchical vision transformer using shifted windows
[C]//
Pre-trained image processing transformer
[C]//
SwinIR: Image restoration using swin transformer
[C]//
Restormer: Efficient transformer for high-resolution image restoration
[C]//
Uformer: A general u-shaped transformer for image restoration
[C]//
Interleaved multishot imaging by spatiotemporal encoding: A fast, self-referenced method for high-definition diffusion and functional MRI
[J].
DOI:10.1002/mrm.25742
PMID:26108165
[本文引用: 2]

Single-shot imaging by spatiotemporal encoding (SPEN) can provide higher immunity to artifacts than its echo planar imaging-based counterparts. Further improvements in resolution and signal-to-noise ratio could be made by rescinding the sequence's single-scan nature. To explore this option, an interleaved SPEN version was developed that was capable of delivering optimized images due to its use of a referenceless correction algorithm.A characteristic element of SPEN encoding is the absence of aliasing when its signals are undersampled along the low-bandwidth dimension. This feature was exploited in this study to segment a SPEN experiment into a number of interleaved shots whose inaccuracies were automatically compared and corrected as part of a navigator-free image reconstruction analysis. This could account for normal phase noises, as well as for object motions during the signal collection.The ensuing interleaved SPEN method was applied to phantoms and human volunteers and delivered high-quality images even in inhomogeneous or mobile environments. Submillimeter functional MRI activation maps confined to gray matter regions as well as submillimeter diffusion coefficient maps of human brains were obtained.We have developed an interleaved SPEN approach for the acquisition of high-definition images that promises a wider range of functional and diffusion MRI applications even in challenging environments.© 2015 Wiley Periodicals, Inc.
Attention is all you need
[C]//
Cvt: Introducing convolutions to vision transformers
[C]//
Incorporating convolution designs into visual transformers
[C]//
The WU-Minn human connectome project: an overview
[J].
DOI:10.1016/j.neuroimage.2013.05.041
PMID:23684880
[本文引用: 1]

The Human Connectome Project consortium led by Washington University, University of Minnesota, and Oxford University is undertaking a systematic effort to map macroscopic human brain circuits and their relationship to behavior in a large population of healthy adults. This overview article focuses on progress made during the first half of the 5-year project in refining the methods for data acquisition and analysis. Preliminary analyses based on a finalized set of acquisition and preprocessing protocols demonstrate the exceptionally high quality of the data from each modality. The first quarterly release of imaging and behavioral data via the ConnectomeDB database demonstrates the commitment to making HCP datasets freely accessible. Altogether, the progress to date provides grounds for optimism that the HCP datasets and associated methods and software will become increasingly valuable resources for characterizing human brain connectivity and function, their relationship to behavior, and their heritability and genetic underpinnings. Copyright © 2013 Elsevier Inc. All rights reserved.