基于物理模型的ISTAVS-Net多线圈MRI图像重建

doi:10.11938/cjmr20243109

基于物理模型的ISTAVS-Net多线圈MRI图像重建

黄敏^,^*, 朱俊琳, 考宇辰, 周到, 唐奇伶

中南民族大学生物医学工程学院，湖北武汉 430074

Multi-Coil MRI Image Reconstruction Based on ISTAVS-Net of Physical Model

HUANG Min^,^*, ZHU Junlin, KAO Yuchen, ZHOU Dao, TANG Qiling

School of Biomedical Engineering, South-Central Minzu University, Wuhan 430074, China

通讯作者: * Tel: 13554286418, E-mail:minhuang@mail.scuec.edu.cn.

收稿日期: 2024-04-15 网络出版日期: 2024-06-28

基金资助:

湖北省自然科学基金资助项目(2020CFB837); 中央高校基本科研业务费专项资金资助项目(CZZ21006); 中央高校基本科研业务费专项资金资助项目(CZQ23032)

Corresponding authors: * Tel: 13554286418, E-mail:minhuang@mail.scuec.edu.cn.

Received: 2024-04-15 Online: 2024-06-28

摘要

提高磁共振成像速度是磁共振领域待解决的问题，采用多线圈扫描是一种常用加速方式．但在加速因子大于4时，传统压缩感知磁共振（CS-MRI）重建算法得到的图像质量不高．为此，本文提出一种基于物理模型的ISTAVS-Net多线圈MRI图像重建方法．将ISTA算法与VS-Net网络拆分思想相结合，提出ISTAVS算法，并展开成ISTAVS-Net网络．将每步迭代与网络模块结合，比黑盒U-Net网络的可解释性更强．网络中引入残差机制，增加了网络的非线性表达能力和稳定性. 稀疏变换、收缩阈值以及正则化参数在训练中自动学习，提高了重建的灵活性．采用Globus膝关节数据集的测试结果表明不同加速因子下ISTAVS-Net网络效果均优于传统的 L1-ESPIRiT和ISTA迭代算法，图像质量和性能指标比U-Net、ISTA-Net+和VS-Net网络提升明显，在高加速因子下对组织细节恢复能力更强．该网络鲁棒性强，更适合对临床扫描数据进行快速高质量重建，可拓宽MRI应用范围．

关键词： 磁共振成像; 物理模型; 图像重建; 多线圈欠采样; 变量拆分网络; 迭代收缩阈值算法

Abstract

How to improve the speed of MRI is a standing problem in the field of magnetic resonance. A commonly used approach for acceleration is multi-coil scan. However, when the acceleration factor exceeds 4, the image quality obtained by traditional compressed sensing magnetic resonance imaging (CS-MRI) reconstruction algorithms becomes unsatisfactory. In this study, we propose a multi-coil MRI image reconstruction method named as ISTAVS algorithm based on physical model. It combines the ISTA algorithm with the splitting idea of VS-Net, and is expanded into an ISTAVS-Net. Each iteration step is combined with the network module, which has higher interpretability than black box U-Net. The residual mechanism is introduced into the ISTAVS-Net to increase the non-linear expression ability and accuracy. Sparse transformation, shrinkage threshold and regularization parameter are automatically learned during training, which increases the flexibility of reconstruction. The test results of the Globus knee dataset show that the ISTAVS-Net outperforms traditional L1-ESPIRiT and ISTA algorithm by multiple indicators, including the improvement of image quality and performance metrics over U-Net, ISTA-Net+ and VS-Net at different acceleration factors, and the ability to recover tissue details at high acceleration factors. The proposed network demonstrates good robustness and is more suitable for fast and high-quality reconstruction of data acquired on clinical MR scanners, thereby can expand the application range of MRI.

Keywords： magnetic resonance imaging; physical model; image reconstruction; multi-coil under-sampling; VS-Net; ISTA algorithm

PDF (1230KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

黄敏, 朱俊琳, 考宇辰, 周到, 唐奇伶. 基于物理模型的ISTAVS-Net多线圈MRI图像重建[J]. 波谱学杂志, 2024, 41(4): 418-429 doi:10.11938/cjmr20243109

HUANG Min, ZHU Junlin, KAO Yuchen, ZHOU Dao, TANG Qiling. Multi-Coil MRI Image Reconstruction Based on ISTAVS-Net of Physical Model[J]. Chinese Journal of Magnetic Resonance, 2024, 41(4): 418-429 doi:10.11938/cjmr20243109

引言

磁共振成像（Magnetic Resonance Imaging，MRI）对软组织分辨率高且不存在辐射危害，是临床常用的检查方式.但MRI主要缺点是成像速度慢，限制了临床使用范围，加速成像一直是MRI领域待解决的问题.成像速度与扫描和重建两个过程有关，使用欠采样可以加快扫描速度，但也使得重建算法变得复杂.

压缩感知技术（Compressed Sensing，CS）^[1]通过利用信号的稀疏性和采集信号与观测矩阵的不相关性^[2]，可以从不遵循采样定理的欠采样 $k$ 空间数据中重建图像，为加速MRI提供了一种新方法．但经典CS-MRI重建算法需手动设置参数，当加速因子（Accelerating Factor，AF）较大时需要长时间迭代运算，重建时间长^[3]，图像质量低，不利于临床诊断．最常见的用于加速MRI成像的一类深度学习网络是基于数据驱动的“端到端映射”网络^[4]，通过输入原始数据或者预处理的图像数据，实现从欠采样数据到全采样数据、欠采样数据到重建图像以及从零填充的伪影图像到重建图像之间的非线性映射．典型的“端到端映射”网络有CNN网络^[5]、实卷积U型网络（U-net）^[6]、复卷积U-net^[7]、双域生成对抗网络（SwinGAN）^[8]、融合注意力机制的多尺度残差U-net网络^[9]、结构不对称的U-net^[10]等．这类网络实现简单，但与物理原理无关，属于黑盒子，缺乏可解释性．

另一类用于加速MRI成像的深度学习网络是基于“物理模型展开”网络^[5]，将CS-MRI物理模型与深度学习网络结合，通过网络模块的堆叠来模拟优化算法的迭代步骤，使网络更具可解释性．2016年，Sun等将交替方向乘子算法（Alternating Direction Method of Multipliers，ADMM）用数据流图展开成ADMM-Net^[11]，首次用网络模块来自动学习模型中的变换和收缩函数．2018年，Hammernik等提出的变分网络^[12]采用CNN网络展开，利用多个卷积核滤波模拟对图像进行多种稀疏化操作，并运用高斯径向基函数模拟势函数求偏导的非线性操作，对迭代梯度下降CS-MRI重建算法进行网络实现，克服了原算法中人工确定稀疏变换和势函数的缺陷．基于“物理模型展开”网络的运用实例还有采用U-net计算线圈灵敏度的端到端 $k$ 域变分网络E2EVarNet^[13]、金字塔卷积网络PC-RNN^[14]、增强深度学习正则化网络MEDL-Net^[15]等．

迭代收缩阈值算法（Iterative Shrinkage-Thresholding Algorithm，ISTA）^[16]是一种基于物理模型的传统CS-MRI算法，可解决稀疏系数的信号恢复问题.Zhang等将ISTA算法展开成ISTA-Net+网络^[17]，采用卷积网络中的卷积操作来学习正则化中的变换函数，使用ReLu非线性变换模拟与稀疏正则化相关的L₁范数.ISTA-Net++网络^[18]则在ISTA-Net+基础上，将ISTA算法与动态展开策略结合，实现了单个模型同时处理不同加速因子的多任务问题.

变量拆分（分裂）网络（Variable Splitting Network，VS-Net）^[19]通过引入辅助变量，将原变量拆分成多个变量，使计算更加高效.VS-Net通过不同的网络模块来对应迭代步骤，网络结构简单，便于端到端训练，但网络训练过程中指标波动较大，迭代次数决定网络的级联数和复杂度，并影响重建图像质量.

为了让网络训练过程更加稳定，提高网络迭代的效率，加快网络训练速度，本研究以VS-Net网络为基本框架，提出一种基于物理模型的ISTAVS-Net多线圈MRI重建网络，做出两项改进：（1）将ISTA算法与VS-Net网络结合，提出了多线圈MRI图像重建的闭合解和深度学习的网络结构，网络的功能模块与迭代过程相对应，可解释性强；（2）在网络输入与输出之间引入残差机制，而且稀疏变换形式、收缩阈值以及正则化参数在训练中自动学习，进一步提高了网络的非线性映射能力.

1 理论

1.1 基于VS-Net的MRI重建模型

香农定理要求采样频率必须大于信号最高频率的2倍，而CS-MRI技术突破了该定理的限制，可以从远低于采样频率的欠采样 $k$ 空间数据中，利用图像在变换域中具有稀疏性的先验知识，采用优化理论算法来恢复图像^[20]．CS-MRI成像模型可表示为：

$y=Ax+\varepsilon$

(1)

其中， $y\in {{C}^{m}}$ 为测量值，表示欠采样的空间数据（ $m\ll n$ ）； $x\in {{C}^{n}}$ 为待重建的MRI图像； $A\in {{C}^{m\times n}}$ 为测量矩阵； $\varepsilon$ 为采样噪声.CS-MRI在工程上更适合以伪随机减少相位编码行来加快扫描，可使用欠采样掩膜 $D\in {{C}^{(m\times n)}}$ 来表达^[21]. $A=DF$ 是傅里叶欠采样算子，F表示傅里叶变换.

现代磁共振扫描仪大都含多个接收线圈，结合多线圈并行采集的CS-MRI的k空间数据可重新写成：

${{y}_{i}}=DF{{S}_{i}}x+\varepsilon,\text{ } i\in \left\{ \text{1,2,}\cdots \text{,}{{N}_{\text{c}}} \right\}$

(2)

其中， ${{y}_{i}}$ 和 ${{S}_{i}}$ 分别为第i个线圈的k空间采集数据和灵敏度信息， ${{N}_{\text{c}}}$ 为线圈总数.

MRI重建任务就是从获得的多线圈采集数据 ${{y}_{i}}$ 中估计出MRI图像x.该问题的优化求解形式为：

$\hat{x}=\underset{x}{\mathop{\arg \min }}\,\frac{1}{2}\left\| DF{{S}_{i}}x-{{y}_{i}} \right\|_{2}^{2}+\lambda R(x)$

(3)

其中， $\left\| DFx-y \right\|_{2}^{2}$ 表示数据一致性项， $R(x)$ 为正则化项， $\lambda$ 为正则化权重.用正则化项来表示某个域的稀疏性，通常可对图像x求全变分，或对x进行小波变换后取L₁范数，或二者皆有^[22].(3)式是从多个线圈的采集数据 ${{y}_{i}}$ 中恢复一幅重建图像x，物理含义不够直接.

若采用VS-Net网络的变量拆分法^[19]，可引入新的辅助变量z和 ${{x}_{i}}$ ，约束条件 $1x=z$ ，是为了将正则化项中的x与数据一致性项中的x分离开.约束条件 $2{{S}_{i}}x={{x}_{i}}$ ， ${{x}_{i}}$ 为每个线圈的图像，是为了把(3)式中求复杂的单变量x问题转变为求简单的多变量 ${{x}_{i}}$ 问题.也就是从多线圈采集数据 ${{y}_{i}}$ 逐一恢复多线圈的重建图像 ${{x}_{i}}$ ，物理含义更加直接简单.

将约束条件写成惩罚项，多线圈CS-MRI模型又变成一个无约束的优化问题，公式为：

$\underset{x,z,{{x}_{i}}}{\mathop{\min }}\,\frac{1}{2}\sum\nolimits_{i=1}^{{{N}_{c}}}{\left\| DF{{x}_{i}}-{{y}_{i}} \right\|_{2}^{2}}+\lambda R(z)+\frac{\alpha }{2}\sum\nolimits_{i=1}^{{{N}_{c}}}{\left\| {{x}_{i}}-{{S}_{i}}x \right\|_{2}^{2}}+\frac{\beta }{2}\left\| z-x \right\|_{2}^{2}$

(4)

其中，α、β为惩罚权重.可用三个子问题优化来求 $z,\ \ {{x}_{i}},\ \ x$ ，公式为：

${{z}^{k+1}}=\underset{z}{\mathop{\arg \min }}\,\frac{1}{2}\left\| z-{{x}^{k}} \right\|_{2}^{2}+\lambda R(z)$

(5.1)

$x_{i}^{k+1}=\underset{{{x}_{i}}}{\mathop{\arg \min }}\,\frac{1}{2}\sum\nolimits_{i=1}^{{{N}_{c}}}{\left\| DF{{x}_{i}}-{{y}_{i}} \right\|}_{2}^{2}+\frac{\alpha }{2}\sum\nolimits_{i=1}^{{{N}_{c}}}{\left\| {{x}_{i}}-{{S}_{i}}{{x}^{k}} \right\|}_{2}^{2}$

(5.2)

$x_{{}}^{k+1}=\underset{x}{\mathop{\arg \min }}\,\frac{\alpha }{2}\sum\nolimits_{i=1}^{{{N}_{c}}}{\left\| x_{i}^{k+1}-{{S}_{i}}x \right\|}_{2}^{2}+\frac{\beta }{2}\left\| {{z}^{k+1}}-x \right\|_{2}^{2}$

(5.3)

其中， $k=\left\{ 1,\ldots,{{N}_{\max }} \right\}$ ， ${{N}_{\max }}$ 为最大迭代数.对 ${{z}^{k+1}}$ ， $x_{i}^{k+1}$ ， $x_{{}}^{k+1}$ 交替迭代获得最优解 $\hat{x}$ .

在VS-Net重建模型中，（5.2）（5.3）式都使用L₂范数，有直接求解法，可通过最小二乘法迭代解决.(5.1)式通过求解最优的 $\hat{z}$ ，以满足约束 $x=z$ ，可归为图像去噪问题.但正则化项R(z)通常为L₁范数，不能使用最小二乘法求解.常规求解(5.1)式需人工选择R(z)和 $\lambda$ 参数，求解困难，鲁棒性差.而且任何固定变换R(z)（如小波、全变差等）都无法对各部位MRI图像实现最优的稀疏变换， $\lambda$ 值对重建图像在数据一致性和平滑度上起着跷跷板的折中效应.所以，人工选取R(z)和 $\lambda$ 存在特异性，算法的泛化能力不强.

针对这一问题，VS-Net网络采用了深度学习的网络模块来学习正则化变换R(z)和权重 $\lambda$ .采用多层卷积与ReLu相组合的操作来实现(5.1)式，卷积对应线性稀疏变换，ReLu对应非线性势函数.该网络的物理可解释性虽然强于端到端的黑盒网络，但网络卷积层数不深，非线性映射能力不强，去噪度不够，使得重建图像在 $R=4$ 时已经变得模糊，影响临床诊断.

1.2 多线圈ISTA改进算法

ISTA是一种用于稀疏优化问题的迭代算法^[16]，已用于实现CS-MRI重建.当正则化用某个线性稀疏变换P域的L₁范数表示时，基于(1)式的CS-MRI的优化表达式为：

$\hat{x}=\underset{x}{\mathop{\arg \min }}\,\frac{1}{2}\left\| Ax-{{y}_{i}} \right\|_{2}^{2}+\lambda R(x)=\underset{x}{\mathop{\arg \min }}\,\frac{1}{2}\left\| Ax-{{y}_{i}} \right\|_{2}^{2}+\lambda {{\left\| Px \right\|}_{1}}$

(6)

其中，非线性正则化变换 $R(x)={{\left\| Px \right\|}_{1}}$ ，(6)式可采用两步更新来迭代求解：

${{r}^{k+1}}={{x}^{k}}-\rho {{A}^{T}}(A{{x}^{k}}-y)$

(7.1)

${{x}^{k+1}}=\underset{x}{\mathop{\arg \min }}\,\frac{1}{2}\left\| x-{{r}^{k+1}} \right\|_{2}^{2}+\lambda {{\left\| Px \right\|}_{1}}$

(7.2)

其中，k为迭代次数， $\rho$ 为步长， ${{x}^{k}}$ 为输入， ${{r}^{k+1}}$ 为中间变量， ${{x}^{k+1}}$ 表示迭代输出.

根据一阶近端原理，(7.2)式的近端映射的表达式和求解方法为：

$\text{prox}{{\text{ }}_{\lambda R}}(r)=\underset{x}{\mathop{\arg \min }}\,\frac{1}{2}\left\| x-r \right\|_{2}^{2}+\lambda R(x)$

(8)

$\hat{x}=\text{prox}{{\text{ }}_{\lambda R}}(r)\text{ }=\tilde{P}(\text{soft}(P(r),\theta ))$

(9)

其中， $P(\cdot )$ 和 $\tilde{P}(\cdot )$ 表示正则化操作 $R(\cdot )$ 中的非线性稀疏变换和稀疏逆变换.是与相关的收缩阈值，在每次迭代都会改变. $\text{soft}(\cdot )$ 为软阈值操作，定义式为：

$\text{soft}(x,\theta )=\text{sign}(x)(|x|-\theta )$

(10)

收缩软阈值操作能有效消除噪声，降低信号波动幅度，同时不让图像平滑过度，很好的保留病灶细节，更有利于疾病的诊断.因此，我们将软阈值拓展到多线圈VS-Net重建中.

(5.1)与(7.2)式结构相同，因此可以快速求解多线圈CS-MRI重建问题的(5.1)式，公式为：

${{z}^{k+1}}=\tilde{P}(\text{soft(}P\text{(}{{x}^{k}}),{{\theta }^{k}}))$

(11)

传统方法需手动设置稀疏变换，如小波变换 $P=W$ ，但不能很好的表达不同部位的稀疏性.深度学习网络能通过卷积等操作自动学习适合不同部位的变换方法，具有更强的灵活性和泛化能力.我们结合深度学习网络来自动学习(11)式中更优的稀疏变换函数P，从而更全面的描述图像的稀疏化.

1.3 ISTAVS-Net重建网络

本文提出一种结合ISTA算法和多线圈VS-Net的优化算法，取名为ISTAVS算法.我们通过(11)式的软阈值操作来实现(5.1)式的去噪功能，将(5)式重新写成完整的闭合解，公式表示为：

${{z}^{k+1}}=\text{denoiser}({{x}^{k}})=\tilde{P}(\text{soft(}P\text{(}{{x}^{k}}),{{\theta }^{k}}))$

(12.1)

$x_{i}^{k+1}={{F}^{-1}}((\alpha I-D)F{{S}_{i}}{{x}^{k}}+D(\lambda F{{S}_{i}}{{x}^{k}}+(1-\lambda ){{D}^{T}}{{y}_{i}})),\text{ }\forall \text{ }i\in \left\{ \text{1,}\cdots \text{,}{{N}_{c}} \right\}$

(12.2)

${{x}^{k+1}}=\beta {{z}^{k+1}}+(1-\beta )\sum\nolimits_{i=1}^{{{N}_{c}}}{{{S}_{i}}x_{i}^{k+1}}$

(12.3)

其中， $\text{denoiser}()$ 为去噪器，用软阈值实现；I为 $n\times n$ 的单位矩阵， ${{D}^{T}}{{y}_{i}}$ 表示第i个线圈的k空间采样值，通过掩膜 $D$ 将未采样位置零填充.(12.2)式实现了k空间数据（频率域）的一致性和空间域图像的一致性；(12.3)式对前两步的输出 ${{z}^{k+1}}$ 和 $x_{i}^{k+1}$ 进行加权平均得到图像 $x_{{}}^{k+1}$ .

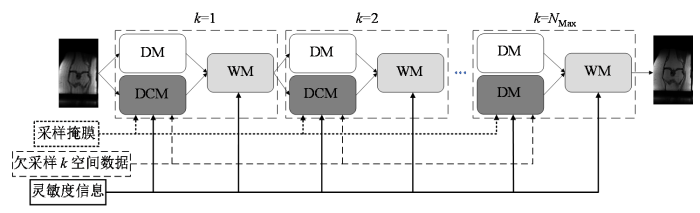
将ISTAVS算法展开搭建成ISTAVS-Net重建网络，结构如图1所示.网络由N_max个子网络级联而成，每个子网络又包含三个模块：收缩阈值去噪模块（Denoising Module，DM）、数据一致性模块（Data Consistency Module，DCM）和加权模块（Weighting Module，WM）.每个模块分别与(12)式中的三步迭代相对应，大大增加了网络的可解释性.迭代次数与网络层数对应，非线性稀疏变换 $P(\cdot )$ 、收缩阈值 ${{\theta }^{k}}$ 、权重 $\lambda$ 、 $\alpha$ 、 $\beta$ 均由网络学习获得，且在每级中是变换的，增加了网络的非线性映射能力.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 ISTAVS-Net的网络结构

Fig. 1 Network structure of ISTAVS-Net

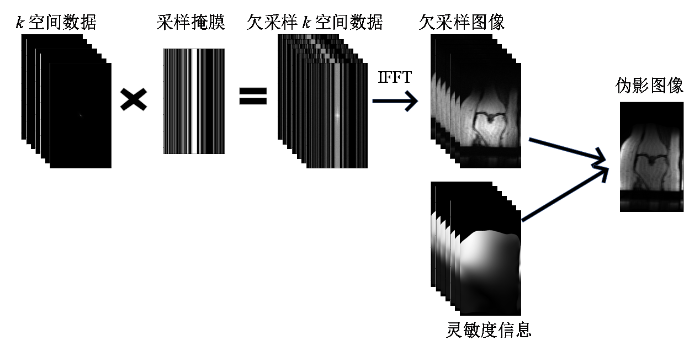
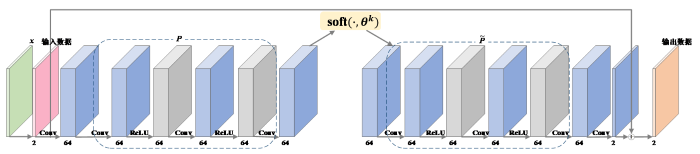
与加速扫描相关的数据有三种：欠采样k空间数据、灵敏度信息、采样掩膜，它们都为多线圈复数数据（ ${{N}_{c}}=15$ ），将其分成实部和虚部两个通道.对于不同的模块，其输入也不同.网络第一级的DM模块的输入用有伪影的初始图像 ${{x}^{0}}$ .所有DCM模块都需要三种数据，而WM模块只需要灵敏度信息，从而保证三次迭代的循环.网络的输出为重建图像，包含实部和虚部两个通道，组成一幅复数图像.

DM为网络的核心模块，其结构如图2所示，由左右两部分及中间的soft $(\cdot )$ 软阈值操作组成.首先经过四次64核3×3卷积和两次ReLu操作对图像进行非线性稀疏变换P $(\cdot )$ ，再对其进行soft $(\cdot )$ 软阈值操作.为了实现P与 $\tilde{P}$ 的正逆变换，该模块在软阈值两端采用左右对称的结构.并在末尾添加了一次2核的卷积，以保证模块输出为2个通道的图像.此外，还在该模块的输入与输出之间引入残差机制，以防止网络在训练时产生梯度爆炸，增强网络的稳定性.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 DM模块结构

Fig. 2 Structure of DM module

DCM模块和WD模块则根据数学公式进行求解，其输出放在网络中作为交替迭代的中间变量.其中涉及的模型参数（收缩阈值 ${{\theta }^{k}}$ 、权重 $\lambda$ 、 $\alpha$ 、 $\beta$ ）用多通道的1×1卷积放在网络的适当位置中，在网络训练中获得，而不是像传统迭代算法中将其人工设定为超参数，因此大大提高了重建的准确度.

本文提出的ISTAVS-Net网络实现MRI图像重建的流程为：

1）首先对输入的伪影图进行预处理，得到DM模块的输入数据 ${{x}^{0}}$ .然后进行卷积、ReLu和soft软阈值操作，模块输出为去噪后的图像 ${{z}^{k+1}}$ .

2）DCM模块先将图像 ${{x}^{k}}$ 与灵敏度信息组合后，得到多个线圈的空间域图像 ${{S}_{i}}{{x}^{k}}$ ，并将其与前一步迭代得到的 ${{x}_{i}}$ 进行空间图像一致性比较.再将多个线圈的空间域图像经FFT（快速傅里叶变换）得到多线圈k空间数据 $DF{{x}_{i}}$ ，并与多线圈采集数据 ${{y}_{i}}$ 进行频域一致性比较.模块输出为更新后的多线圈重建图像 $x_{i}^{k+1}$ .

3）将前两步得到的输出结果与灵敏度图像一起送入WM模块，将灵敏度加权的多线圈图像 $x_{i}^{k+1}$ 与去噪图像 $z_{{}}^{k+1}$ 一起进行加权平均，模块输出为更新后的重建图像 $x_{{}}^{k+1}$ .

4）重复前面三个步骤，直到第 ${{N}_{\max }}$ 次迭代之后得到网络的输出，即重建图像x.

2 模型实现与训练

2.1 数据集预处理

本研究使用的数据集来自Globus网站公开的NYULH Radiology Reconstruction Data临床膝关节数据集(https://app.globus.org)．数据集为多线圈 $k$ 空间数据以及对应的线圈灵敏度，包含20位病人数据，每位病人大约扫描40层，每层都包含了15个线圈的成对信息，数据大小均为640×368．使用了冠状位和轴位数据，k空间数据维度分别为（640×368）和（640×484），均按照7:2:1划分为训练集、验证集和测试集．

本研究使用笛卡尔采样，分别仿真设计了在相位编码方向进行2、4、6和8倍加速下的欠采样掩膜，在中心区域保留24行全采样数据信息，周围进行随机欠采样.

为了获得网络的输入数据，首先对多线圈 $k$ 空间数据进行加速扫描，得到欠采样k空间数据；再经过快速傅里叶逆变换（IFFT），得到经过零填充的多线圈图像数据．并将其与灵敏度信息进行加权组合，得到初始的输入数据．以4倍加速下的扫描过程为例，获取欠采样数据和网络输入初始图像的过程如图3所示．

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 加速扫描的仿真过程

Fig. 3 Simulation of under-sampling process

网络输入为重建图像的初始值 ${{x}^{0}}$ ，送到第一级的DM和DCM模块.用多个线圈的欠采样图像进行灵敏度加权来得到初始的伪影图像 ${{x}^{0}}$ ，公式为：

${{x}^{0}}=\sum\nolimits_{i=1}^{{{N}_{c}}}{S_{i}^{H}(\tilde{F}}{{D}^{T}}{{y}_{i}})$

(13)

其中， ${{y}_{i}}$ 表示第i个线圈的k空间数据， $\tilde{F}$ 为反傅里叶变换.将k空间全采集数据经过欠采样和反傅里叶变换后得到欠采样图像，再将欠采样图像与对应灵敏度图像相乘得到新的图像，即为网络的初始输入.

2.2 实验环境与评价指标

本研究使用Python编程，在Pytorch框架下完成网络的训练与测试.网络批次大小设为4，初始学习率为0.001，学习率每30轮衰减一半.使用Adam优化器，指数衰减率为 ${{\beta }_{1}}=0.9$ 和 ${{\beta }_{2}}=0.999$ ，训练轮数epochs设为200.ISTAVS-Net网络使用的损失函数loss包含重建损失 ${{L}_{\text{rec}}}$ 和对称约束损失 ${{L}_{\text{cons}}}$ ，公式为：

$\text{loss}={{L}_{\text{rec}}}+\gamma {{L}_{\text{cons}}}$

(14)

其中， ${{L}_{\text{rec}}}$ 采用重建结果与金标准图像之间的均方误差计算， ${{L}_{\text{cons}}}$ 用于使网络去噪模块中的稀疏变换和逆变换满足对称约束 $(P\odot \tilde{P}=I)$ ，权重 $\gamma$ 用于平衡两种损失.两种损失的计算公式分别为：

$\begin{matrix} & {{L}_{\text{rec}}}=\frac{1}{N\cdot {{N}_{b}}}\sum\nolimits_{i=1}^{{{N}_{b}}}{\left\| {{x}_{i}}-{{r}_{i}} \right\|}_{2}^{2} \\ & {{L}_{\text{cons}}}=\frac{1}{N\cdot {{N}_{b}}}\sum\nolimits_{i=1}^{{{N}_{b}}}{\sum\nolimits_{k=\text{1}}^{{{N}_{\text{max}}}}{\left\| {{{\tilde{P}}}_{k}}({{P}_{k}}({{x}_{i}})-{{x}_{i}}) \right\|}}_{2}^{2} \\ \end{matrix}$

(15)

其中， $x_{i}^{{}}$ 为重建图像， ${{r}_{i}}$ 为参考的金标准图像，N为一个训练批次的样本数， ${{N}_{b}}$ 为训练块数， ${{N}_{\max }}$ 为网络的级联次数， $\gamma$ 为平衡参数，设置为0.01.

对重建图像质量的评价采用MRI重建领域常用的3个指标^[23]，归一化均方误差（Normalized Mean Square Error，NMSE）、峰值信噪比（Peak Signal-To-Noise Ratio，PSNR）和结构相似性（Structure Similarity Index Measurement，SSIM），且所有指标均采用测试数据的指标平均值来表示.指标计算的公式分别为：

$\text{NMSE}(x,\hat{x})=\frac{\left\| \hat{x}-x \right\|_{2}^{2}}{||x||_{2}^{2}}$

(16)

$\text{PSNR}(x,\hat{x})=10{{\log }_{10}}\left( \frac{{{[\max (x)]}^{2}}}{\frac{1}{N}\sum\nolimits_{i,j}{{{\left( {{x}_{i,j}}-{{{\hat{x}}}_{i,j}} \right)}^{2}}}} \right)$

(17)

$\text{SSIM}(x,\hat{x})=\frac{(2{{\mu }_{x}}{{\mu }_{{\hat{x}}}}+{{c}_{1}})(2{{\sigma }_{x}}{{\sigma }_{{\hat{x}}}}+{{c}_{2}})({{\operatorname{cov}}_{x\hat{x}}}+{{c}_{3}})}{(\mu _{x}^{2}+\mu _{{\hat{x}}}^{2}+{{c}_{1}})(\sigma _{x}^{2}+\sigma _{{\hat{x}}}^{2}+{{c}_{2}})(\sigma _{x}^{{}}+\sigma _{{\hat{x}}}^{{}}+{{c}_{3}})}$

(18)

其中，x代表金标准图像， $\hat{x}$ 代表重建图像，max(x)为图像最大值， $\mu$ 为图像均值，N为图像像素总数.σ为图像方差，cov表示两个图像之间的协方差， ${{c}_{i}}$ 为常数.

3 结果与分析

经过大量对比实验发现，随着网络级联（迭代）数增加，网络学习能力增强，重建图像更优.当级联数大于9时，网络性能的改善并不明显.考虑到网络复杂度、学习参数量及训练时间，将网络级联数设为9.ESPIRiT算法是多线圈CS-MRI传统重建算法的标杆^[24]，可采用小波变换的L₁范数作为正则化项（即：L1-ESPIRiT）.为了评估提出的ISTAVS-Net网络的可行性和性能，将其与两种传统算法（L1-ESPIRiT、ISTA^[16]）和三种深度学习网络（端到端U-Net网络^[23]、ISTA-Net+网络^[17]、VS-Net网络^[19]）进行比较.

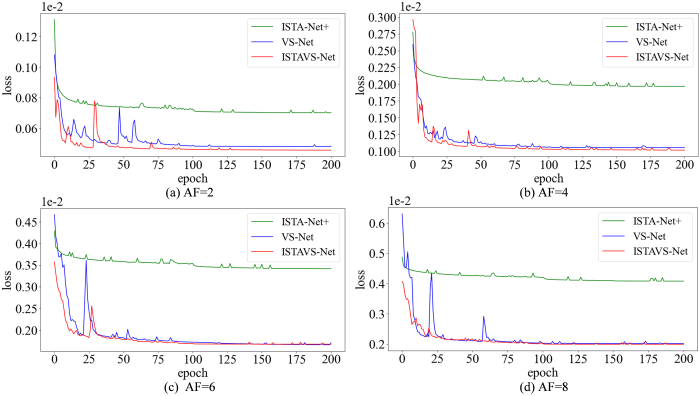
图4为基于模型的三种深度学习网络（ISTA-Net+、VS-Net、ISTAVS-Net）在冠状位数据中的训练损失曲线.ISTA-Net+、VS-Net、ISTAVS-Net网络训练时间分别为10 h 20 min、9 h 30 min、12 h 20 min，网络训练参数量分别为0.986 M、0.782 M、1.018 M.从图4可见，在各加速因子下，三种网络在130轮后都收敛稳定.VS-Net的训练损失值（蓝色）虽远小于ISTA-Net+网络（绿色），但训练中波动较大.本文提出的ISTAVS-Net损失值（红线）在三者中最小，并且在AF=4, 6, 8时比VS-Net（蓝线）震荡的波峰幅值降低，收敛更快速平滑.可见，VS-Net的变量拆分可使重建图像质量更优，而ISTA采用收缩软阈值去噪使网络收敛更快更平稳，ISTAVS-Net在结合ISTA去噪后，稳定性比VS-Net得到了较大提升.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 加速因子为(a) 2、(b) 4、(c) 6、(d) 8时ISTA-Net+、VS-Net、ISTAVS-Net网络的训练损失曲线

Fig. 4 Training loss curves of ISTA-Net+,VS-Net and ISTAVS-Net with AF of (a) 2, (b) 4, (c) 6, and (d) 8

表1为两种传统算法（L1-ESPIRiT、ISTA）和4种深度学习网络（U-Net、ISTA-Net+、VS-Net、ISTAVS-Net）在冠状位数据重建结果中的评价指标（PSNR、SSIM、NMSE）的平均值.从表1中可见，4种深度学习网络的性能指标均优于传统算法.且本文提出的ISTAVS-Net网络相较于另外三种深度学习网络，性能指标均有提高.两种算法和四种深度学习网络的性能排序为：ISTAVS-Net>U-Net>VS-Net>ISTA-Net+>ISTA>L1-ESPIRiT.比较不同加速因子下评价指标可见，当AF=2时，四种网络差距较小，PSNR均超过40 dB.AF=4时，ISTAVS-Net的PSNR达到了37.724 dB，相比另三种网络有较大提升.AF=6时，ISTAVS-Net的SSIM依旧能保持在0.9以上.在高加速因子（AF=8）下，ISTAVS-Net的重建指标虽然也最好，但网络指标值下降较为明显.

表1 两种传统算法（L1-ESPIRiT、ISTA）和4种深度学习网络（U-Net、ISTA-Net+、VS-Net、ISTAVS-Net）在冠状位数据重建结果中的评价指标平均值

Table 1 Average evaluation metrics of two traditional algorithms (L1-ESPIRiT, ISTA) and four deep learning networks (U-Net, ISTA-Net+, VS-Net, ISTAVS-Net) in coronary data reconstruction results

评价指标	AF	L1-ESPIRiT	ISTA	U-Net	ISTA-Net+	VS-Net	ISTAVS-Net
PSNR/dB	2	32.671	34.051	40.926	40.879	40.675	42.021
	4	28.868	30.390	36.911	36.281	36.478	37.724
	6	27.234	29.567	34.052	33.808	33.932	34.609
	8	26.976	28.446	33.287	32.713	33.184	33.341
SSIM	2	0.8802	0.9301	0.9573	0.9470	0.9547	0.9604
	4	0.8275	0.8680	0.9257	0.9128	0.9208	0.9311
	6	0.7608	0.8424	0.8950	0.8807	0.8936	0.9002
	8	0.7020	0.8205	0.8825	0.8679	0.8833	0.8839
NMSE	2	0.0205	0.0160	0.0107	0.0113	0.0109	0.0105
	4	0.0384	0.0362	0.0189	0.0193	0.0190	0.0183
	6	0.0478	0.0438	0.0277	0.0280	0.0275	0.0271
	8	0.0578	0.0567	0.0347	0.0350	0.0316	0.0304

新窗口打开| 下载CSV

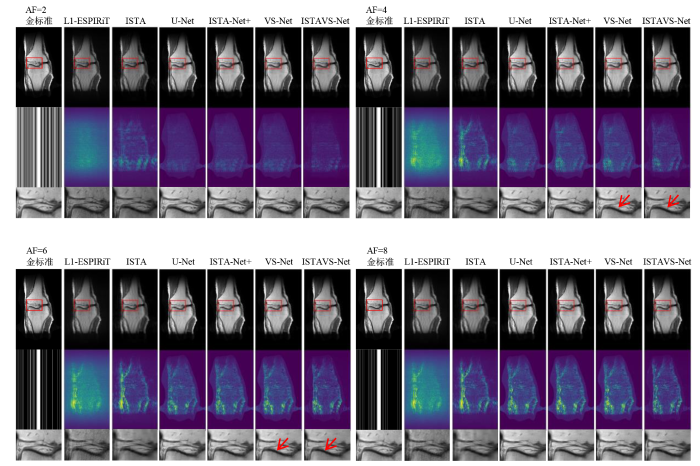
图5为AF=2, 4, 6和8时，两种传统算法和四种深度学习网络在冠状位数据中的重建结果.第一行为金标准图像和六种重建图像，第二行为欠采样mask和误差图像，第三行为第一行中红色框内的放大图.从图中可见，在AF不高时，四种深度学习网络都得到了很好的重建图像.而传统算法只有在AF=2时较好，AF=4时结果已出现很强的伪影，不适于临床.而提出的ISTAVS-Net误差最小，图像细节恢复更好.在AF=4时，红色方框处ISTAVS-Net重建结果明显更清晰，伪影更少，红色箭头处的软骨损伤清晰可见.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 两种传统算法和四种深度学习网络在冠状位数据中的重建结果（左上：AF=2，右上：AF=4，左下：AF=6，右下：AF=8）

Fig. 5 Reconstruction results of two traditional algorithms and four deep learning networks in coronary data (upleft: AF=2, upright: AF=4, down left: AF=6, down right: AF=8)

AF=6和8时，传统算法的重建结果已很难应用于临床.在AF为6时，四种深度学习网络都能重建出图像，可区分不同组织.但随着AF增大，误差图变亮，图像质量变差，AF=8时折叠伪影较为严重.可见，高加速因子下（AF=8），四种深度学习网络都不能完全消除伪影.但ISTAVS-Net重建图像的折叠伪影相对更轻，对图像细节的恢复在四者中也是最强的.

表1和图5的测试结果证明提出的ISTAVS-Net网络在冠状位数据中的重建效果很好.为了验证该网络在其他方位重建的泛化，我们还对轴位数据集在6倍加速下的网络进行训练和测试，并与冠状位重建结果进行比较.同时展示了传统算法L1-ESPIRiT和ISTA的重建结果以便比较.两种数据集的重建评价指标平均值如表2所示.ISTAVS-Net网络的重建指标均远优于传统算法，且轴位和冠状位的SSIM值分别为0.938 2和0.900 2.相比冠状位，轴位重建效果更好，PSNR值更高，能达到38.952 dB.ISTAVS-Net重建时间只需1~2 s，比L1-ESPIRiT（~3 min）和ISTA（~80 s）快很多，且重建质量明显优于传统算法.

表2 轴位和冠状位的评价指标对比

Table 2 Evaluation metrics in axial view and coronal view

	轴位			冠状位
	L1-ESPIRiT	ISTA	ISTAVS-Net	L1-ESPIRiT	ISTA	ISATVS-Net
PSNR/dB	31.743	34.051	38.952		27.234	29.567	34.609
SSIM	0.8180	0.9089	0.9382	0.7608	0.8424	0.9002
NMSE	0.0467	0.0395	0.0227	0.0478	0.0438	0.0271
Times/s	196.12	71.66	2.11	153.95	80.13	1.04

新窗口打开| 下载CSV

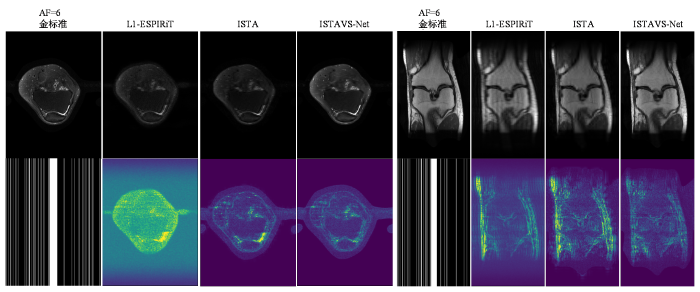
图6为AF=6时，一例病人的轴位与冠状位的重建图像对比图.两个方位的L1-ESPIRiT和ISTA重建图像都更模糊，信噪比较低，但ISTA算法优于L1-ESPIRiT.本文提出的ISTAVS-Net重建质量最优，组织边缘更清晰，消除了冠状位的大部分伪影.可见，ISTAVS-Net对两个不同扫描方位的重建效果均比传统算法提升了很多，网络泛化能力很强.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 AF=6时轴位与冠状位的重建结果对比（左：轴位，右：冠状位）

Fig 6 Reconstruction results based on AF=6 (left: sagittal, right: transverse)

4 结论

本文提出了一种在VS-Net基础上结合ISTA去噪的ISTAVS-Net，实现了对多线圈CS-MRI加速采集数据的图像重建.ISTAVS-Net包含了两方面的改进：（1）相比使用简单卷积操作因而去噪不彻底的VS-Net，ISTAVS-Net使用改进的多线圈ISTA算法实现去噪模块，迭代软阈值去噪效果明显，能保持图像细节. （2）在去噪模块的输入与输出之间引入残差机制，避免了网络在训练中可能出现的梯度问题和性能退化，增加网络的非线性映射能力，提高了重建的准确性和稳定性.

ISTAVS-Net是基于CS-MRI物理模型的，相比于黑盒网络，可解释性更强.且模型参数和正则化项都能自动学习，而非人为选取.网络在AF≤6时重建的图像质量高，能兼顾定量指标与视觉效果.基于模型的网络比传统迭代方法具有更好的灵活性，能提高MRI重建质量，推动了传统算法与网络模型的结合，这在工程中也更具实际意义.

当加速因子过高时（AF=8），虽然网络评价指标值较好，但图像伪影并不能完全消除，会影响临床诊断.后续可重新设计加速扫描方式、结合双域加速^[25]等手段来优化网络，以获得更优的重建图像.总之，使用深度学习网络的方法实现MRI重建还存在许多问题尚未解决，离临床落地还有较远的路要走.

利益冲突

无

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

LUSTIG

, DONOHO

, PAULY

J M

Sparse MRI: The application of compressed sensing for rapid MR imaging

[J]. Magn Reson Med, 2007, 58(6): 1182-1195.

DOI:10.1002/mrm.21391 PMID:17969013 [本文引用: 1]

The sparsity which is implicit in MR images is exploited to significantly undersample k-space. Some MR images such as angiograms are already sparse in the pixel representation; other, more complicated images have a sparse representation in some transform domain-for example, in terms of spatial finite-differences or their wavelet coefficients. According to the recently developed mathematical theory of compressed-sensing, images with a sparse representation can be recovered from randomly undersampled k-space data, provided an appropriate nonlinear recovery scheme is used. Intuitively, artifacts due to random undersampling add as noise-like interference. In the sparse transform domain the significant coefficients stand out above the interference. A nonlinear thresholding scheme can recover the sparse coefficients, effectively recovering the image itself. In this article, practical incoherent undersampling schemes are developed and analyzed by means of their aliasing interference. Incoherence is introduced by pseudo-random variable-density undersampling of phase-encodes. The reconstruction is performed by minimizing the l(1) norm of a transformed image, subject to data fidelity constraints. Examples demonstrate improved spatial resolution and accelerated acquisition for multislice fast spin-echo brain imaging and 3D contrast enhanced angiography.(c) 2007 Wiley-Liss, Inc.

[2]

SONG

, SHEN

, XING

, et al.

Solving inverse problems in medical imaging with score-based generative models

[J]. arXiv preprint, arXiv: 2111.08005, 2021.

[本文引用: 1]

[3]

GENG

C H

, JIANG

M F

, FANG

, et al.

HFIST-Net: High-throughput fast iterative shrinkage thresholding network for accelerating MR image reconstruction

[J]. Comput Meth Prog Bio, 2023, 232: 107440.

[本文引用: 1]

[4]

PAL

, RATHI

A review and experimental evaluation of deep learning methods for MRI reconstruction

[J]. J Mach Learn Biomed Imaging, 2022, 1: 001.

[本文引用: 1]

[5]

WANG

, SU

, YING

, et al.

Accelerating magnetic resonance imaging via deep learning

[C]// 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI), Prague, Czech Republic: IEEE, 2016: 514-517.

[本文引用: 2]

[6]

JIN

K H

, MCCANN

M T

, FROUSTEY

, et al.

Deep convolutional neural network for inverse problems in imaging

[J]. IEEE Trans Image Process, 2017, 26(9): 4509-4522.

[本文引用: 1]

[7]

ELIZABETH

, JOSEPH

, JOHN

, et al.

Analysis of deep complex-valued convolutional neural networks for MRI reconstruction and phase-focused applications

[J]. Magn Reson Med, 2021, 86(2):1093-1109.

DOI:10.1002/mrm.28733 PMID:33724507 [本文引用: 1]

Deep learning has had success with MRI reconstruction, but previously published works use real-valued networks. The few works which have tried complex-valued networks have not fully assessed their impact on phase. Therefore, the purpose of this work is to fully investigate end-to-end complex-valued convolutional neural networks (CNNs) for accelerated MRI reconstruction and in several phase-based applications in comparison to 2-channel real-valued networks.Several complex-valued activation functions for MRI reconstruction were implemented, and their performance was compared. Complex-valued convolution was implemented and tested on an unrolled network architecture and a U-Net-based architecture over a wide range of network widths and depths with knee, body, and phase-contrast datasets.Quantitative and qualitative results demonstrated that complex-valued CNNs with complex-valued convolutions provided superior reconstructions compared to real-valued convolutions with the same number of trainable parameters for both an unrolled network architecture and a U-Net-based architecture, and for 3 different datasets. Complex-valued CNNs consistently had superior normalized RMS error, structural similarity index, and peak SNR compared to real-valued CNNs.Complex-valued CNNs can enable superior accelerated MRI reconstruction and phase-based applications such as fat-water separation, and flow quantification compared to real-valued convolutional neural networks.© 2021 International Society for Magnetic Resonance in Medicine.

[8]

ZHAO

, YANG

, LI

, et al.

SwinGAN: A dual-domain swin transformer-based generative adversarial network for MRI reconstruction

[J]. Comput Biol Med, 2023, 153: 106513.

[本文引用: 1]

[9]

Y J

, YANG

X Y

, YANG

X M

Magnetic resonance image reconstruction of multi-scale residual Unet fused with attention mechanism

[J]. Chinese J Magn Reson, 2023, 40(3): 307-319.

[本文引用: 1]

李奕洁, 杨馨雨, 杨晓梅.

融合注意力机制的多尺度残差Unet的磁共振图像重建

[J]. 波谱学杂志, 2023, 40(3): 307-319.

DOI:10.11938/cjmr20223040 [本文引用: 1]

为了提高磁共振图像在欠采样下重建的质量，本文融合注意力机制和多尺度残差卷积构建Unet网络，实现磁共振图像在欠采样下的重建算法．为增强网络特征的表现能力，以及防止网络训练中梯度消失与退化的问题，在Unet网络的编码路径中引入多尺度残差卷积，提取不同尺度的特征信息；为能准确地恢复图像的细节纹理特征，在Unet网络编码和解码路径的跳层拼接部分引入卷积注意力块，对细节纹理等关键信息进行不同程度的响应．实验表明，本文方法可通过欠采样k-空间数据快速重建出细节纹理清晰且无重叠伪影的高质量磁共振图像．

[10]

SHI

W C

, JIN

Z Y

, YE

Fast multi-channel magnetic resonance imaging based on PCAU-Net

[J]. Chinese J Magn Reson, 2023, 40(1): 39-51.

[本文引用: 1]

施伟成, 金朝阳, 叶铮.

基于PCAU-Net的快速多通道磁共振成像方法

[J]. 波谱学杂志, 2023, 40(1): 39-51.

DOI:10.11938/cjmr20222992 [本文引用: 1]

多通道磁共振成像方法采用多个接收线圈同时欠采样k空间以加快成像速度，并基于后处理算法重建图像，但在较高加速因子时，其图像重建质量仍然较差．本文提出了一种基于PCAU-Net的快速多通道磁共振成像方法，将单通道实数U型卷积神经网络拓展到多通道复数卷积神经网络，设计了一种结构不对称的U型网络结构，通过在解码部分减小网络规模以降低模型的复杂度．PCAU-Net网络在跳跃连接前增加了1×1卷积，以实现跨通道信息交互．输入和输出之间利用残差连接为误差的反向传播提供捷径．实验结果表明，使用规则和随机采样模板，在不同加速因子时，相比常规的GRAPPA重建算法和SPIRiT重建方法，本文提出的PCAU-Net方法可高质量重建出磁共振复数图像，并且相比于PCU-Net方法，PCAU-Net减少了模型参数、缩短了训练时间．

[11]

YANG

, SUN

, LI

H B

, et al.

Deep ADMM-Net for compressive sensing MRI

[C]// Advances in neural information processing systems, Barcelona, Spain, 2016: 10-18.

[本文引用: 1]

[12]

HAMMERNIK

, KLATZER

, KOBLER

, et al.

Learning a variational network for reconstruction of accelerated MRI data

[J]. Magn Reson Med, 2018, 79(6): 3055-3071.

DOI:10.1002/mrm.26977 PMID:29115689 [本文引用: 1]

To allow fast and high-quality reconstruction of clinical accelerated multi-coil MR data by learning a variational network that combines the mathematical structure of variational models with deep learning.Generalized compressed sensing reconstruction formulated as a variational model is embedded in an unrolled gradient descent scheme. All parameters of this formulation, including the prior model defined by filter kernels and activation functions as well as the data term weights, are learned during an offline training procedure. The learned model can then be applied online to previously unseen data.The variational network approach is evaluated on a clinical knee imaging protocol for different acceleration factors and sampling patterns using retrospectively and prospectively undersampled data. The variational network reconstructions outperform standard reconstruction algorithms, verified by quantitative error measures and a clinical reader study for regular sampling and acceleration factor 4.Variational network reconstructions preserve the natural appearance of MR images as well as pathologies that were not included in the training data set. Due to its high computational performance, that is, reconstruction time of 193 ms on a single graphics card, and the omission of parameter tuning once the network is trained, this new approach to image reconstruction can easily be integrated into clinical workflow. Magn Reson Med 79:3055-3071, 2018. © 2017 International Society for Magnetic Resonance in Medicine.© 2017 International Society for Magnetic Resonance in Medicine.

[13]

SRIRAM

, ZBONTAR

, MURRELL

, et al.

End-to-end variational networks for accelerated MRI reconstruction

[J]. arXiv preprint, arxiv: 2004.06688, 2020.

[本文引用: 1]

[14]

CHEN

E Z

, WANG

, CHEN

, et al.

Pyramid convolutional RNN for MRI image reconstruction

[J]. IEEE Trans Med Imag, 2022, 41(8): 2033-2047.

[本文引用: 1]

[15]

QIAO

, HUANG

, LI

MEDL-Net: A model-based neural network for MRI reconstruction with enhanced deep learned regularizers

[J]. Magn Reson Med, 2023, 89(5): 2062-2075.

[本文引用: 1]

[16]

BECK

, TEBOULLE

A fast iterative shrinkage-thresholding algorithm for linear inverse problems

[J]. SIAM J Imaging Sci, 2009, 2(1): 183-202.

[本文引用: 3]

[17]

ZHANG

, GHANEM

ISTA-Net: Interpretable optimization-inspired deep network for image compressive sensing

[C]// IEEE conference on computer vision and pattern recognition, Salt Lake City, USA: IEEE, 2018: 1828-1837.

[本文引用: 2]

[18]

YOU

, XIE

, ZHANG

ISTA-NET++: Flexible deep unfolding network for compressive sensing

[C]// IEEE International Conference on Multimedia and Expo, Shenzhen, China: IEEE, 2021: 1-6.

[本文引用: 1]

[19]

DUAN

, SCHLEMPER

, QIN

, et al.

VS-Net: variable splitting network for accelerated parallel MRI reconstruction

[C]// International Conference on Medical Image Computing and Computer-Assisted Intervention, Shenzhen, China: Springer, 2019: 713-722.

[本文引用: 3]

[20]

J C

Compressed sensing MRI: A review from signal processing perspective

[J]. BMC Biomedical Engineering, 2019, 1(1): 1-17.

[本文引用: 1]

[21]

ARGHYA

, YOGESH

A review and experimental evaluation of deep learning methods for MRI reconstruction

[J]. J Mach Learn Biomed Imaging, 2022, 3: 1-55.

[本文引用: 1]

[22]

CHEN

, SHAH

N J

, WORTHOFF

W A

Compressed sensing in sodium magnetic resonance imaging: techniques, applications, and future prospects

[J]. J Magn Reson Imaging, 2022, 55(5): 1340-1356.

[本文引用: 1]

[23]

JURE

, FLORIAN

, ANUROOP

, et al.

FastMRI: an open dataset and benchmarks for accelerated MRI

[J]. arXiv preprint, arXiv: 1811.08839, 2019.

[本文引用: 2]

[24]

PENG

, MARK

, MICHAEL

, et al.

ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA

[J]. Magn Reson Med, 2014, 71(3): 990-1001.

[本文引用: 1]

[25]

HONG

, WEI

, MORLEY

, et al.

Dual-domain accelerated MRI reconstruction using transformers with learning-based undersampling

[J]. Comput Med Imag Graph, 2023, 106: 102206.

[本文引用: 1]

Sparse MRI: The application of compressed sensing for rapid MR imaging

2007

... 压缩感知技术（Compressed Sensing，CS）^[1]通过利用信号的稀疏性和采集信号与观测矩阵的不相关性^[2]，可以从不遵循采样定理的欠采样

$k$

空间数据中重建图像，为加速MRI提供了一种新方法．但经典CS-MRI重建算法需手动设置参数，当加速因子（Accelerating Factor，AF）较大时需要长时间迭代运算，重建时间长^[3]，图像质量低，不利于临床诊断．最常见的用于加速MRI成像的一类深度学习网络是基于数据驱动的“端到端映射”网络^[4]，通过输入原始数据或者预处理的图像数据，实现从欠采样数据到全采样数据、欠采样数据到重建图像以及从零填充的伪影图像到重建图像之间的非线性映射．典型的“端到端映射”网络有CNN网络^[5]、实卷积U型网络（U-net）^[6]、复卷积U-net^[7]、双域生成对抗网络（SwinGAN）^[8]、融合注意力机制的多尺度残差U-net网络^[9]、结构不对称的U-net^[10]等．这类网络实现简单，但与物理原理无关，属于黑盒子，缺乏可解释性． ...

Solving inverse problems in medical imaging with score-based generative models

... 压缩感知技术（Compressed Sensing，CS）^[1]通过利用信号的稀疏性和采集信号与观测矩阵的不相关性^[2]，可以从不遵循采样定理的欠采样

$k$

HFIST-Net: High-throughput fast iterative shrinkage thresholding network for accelerating MR image reconstruction

2023

... 压缩感知技术（Compressed Sensing，CS）^[1]通过利用信号的稀疏性和采集信号与观测矩阵的不相关性^[2]，可以从不遵循采样定理的欠采样

$k$

A review and experimental evaluation of deep learning methods for MRI reconstruction

2022

... 压缩感知技术（Compressed Sensing，CS）^[1]通过利用信号的稀疏性和采集信号与观测矩阵的不相关性^[2]，可以从不遵循采样定理的欠采样

$k$

Accelerating magnetic resonance imaging via deep learning

2016

... 压缩感知技术（Compressed Sensing，CS）^[1]通过利用信号的稀疏性和采集信号与观测矩阵的不相关性^[2]，可以从不遵循采样定理的欠采样

$k$

... 另一类用于加速MRI成像的深度学习网络是基于“物理模型展开”网络^[5]，将CS-MRI物理模型与深度学习网络结合，通过网络模块的堆叠来模拟优化算法的迭代步骤，使网络更具可解释性．2016年，Sun等将交替方向乘子算法（Alternating Direction Method of Multipliers，ADMM）用数据流图展开成ADMM-Net^[11]，首次用网络模块来自动学习模型中的变换和收缩函数．2018年，Hammernik等提出的变分网络^[12]采用CNN网络展开，利用多个卷积核滤波模拟对图像进行多种稀疏化操作，并运用高斯径向基函数模拟势函数求偏导的非线性操作，对迭代梯度下降CS-MRI重建算法进行网络实现，克服了原算法中人工确定稀疏变换和势函数的缺陷．基于“物理模型展开”网络的运用实例还有采用U-net计算线圈灵敏度的端到端

$k$

域变分网络E2EVarNet^[13]、金字塔卷积网络PC-RNN^[14]、增强深度学习正则化网络MEDL-Net^[15]等． ...

Deep convolutional neural network for inverse problems in imaging

2017

... 压缩感知技术（Compressed Sensing，CS）^[1]通过利用信号的稀疏性和采集信号与观测矩阵的不相关性^[2]，可以从不遵循采样定理的欠采样

$k$

Analysis of deep complex-valued convolutional neural networks for MRI reconstruction and phase-focused applications

2021

... 压缩感知技术（Compressed Sensing，CS）^[1]通过利用信号的稀疏性和采集信号与观测矩阵的不相关性^[2]，可以从不遵循采样定理的欠采样

$k$

SwinGAN: A dual-domain swin transformer-based generative adversarial network for MRI reconstruction

2023

... 压缩感知技术（Compressed Sensing，CS）^[1]通过利用信号的稀疏性和采集信号与观测矩阵的不相关性^[2]，可以从不遵循采样定理的欠采样

$k$

Magnetic resonance image reconstruction of multi-scale residual Unet fused with attention mechanism

2023

... 压缩感知技术（Compressed Sensing，CS）^[1]通过利用信号的稀疏性和采集信号与观测矩阵的不相关性^[2]，可以从不遵循采样定理的欠采样

$k$

融合注意力机制的多尺度残差Unet的磁共振图像重建

2023

... 压缩感知技术（Compressed Sensing，CS）^[1]通过利用信号的稀疏性和采集信号与观测矩阵的不相关性^[2]，可以从不遵循采样定理的欠采样

$k$

Fast multi-channel magnetic resonance imaging based on PCAU-Net

2023

... 压缩感知技术（Compressed Sensing，CS）^[1]通过利用信号的稀疏性和采集信号与观测矩阵的不相关性^[2]，可以从不遵循采样定理的欠采样

$k$

基于PCAU-Net的快速多通道磁共振成像方法

2023

... 压缩感知技术（Compressed Sensing，CS）^[1]通过利用信号的稀疏性和采集信号与观测矩阵的不相关性^[2]，可以从不遵循采样定理的欠采样

$k$

Deep ADMM-Net for compressive sensing MRI

2016

$k$

域变分网络E2EVarNet^[13]、金字塔卷积网络PC-RNN^[14]、增强深度学习正则化网络MEDL-Net^[15]等． ...

Learning a variational network for reconstruction of accelerated MRI data

2018

$k$

域变分网络E2EVarNet^[13]、金字塔卷积网络PC-RNN^[14]、增强深度学习正则化网络MEDL-Net^[15]等． ...

End-to-end variational networks for accelerated MRI reconstruction

$k$

域变分网络E2EVarNet^[13]、金字塔卷积网络PC-RNN^[14]、增强深度学习正则化网络MEDL-Net^[15]等． ...

Pyramid convolutional RNN for MRI image reconstruction

2022

$k$

域变分网络E2EVarNet^[13]、金字塔卷积网络PC-RNN^[14]、增强深度学习正则化网络MEDL-Net^[15]等． ...

MEDL-Net: A model-based neural network for MRI reconstruction with enhanced deep learned regularizers

2023

$k$

域变分网络E2EVarNet^[13]、金字塔卷积网络PC-RNN^[14]、增强深度学习正则化网络MEDL-Net^[15]等． ...

A fast iterative shrinkage-thresholding algorithm for linear inverse problems

2009

... 迭代收缩阈值算法（Iterative Shrinkage-Thresholding Algorithm，ISTA）^[16]是一种基于物理模型的传统CS-MRI算法，可解决稀疏系数的信号恢复问题.Zhang等将ISTA算法展开成ISTA-Net+网络^[17]，采用卷积网络中的卷积操作来学习正则化中的变换函数，使用ReLu非线性变换模拟与稀疏正则化相关的L₁范数.ISTA-Net++网络^[18]则在ISTA-Net+基础上，将ISTA算法与动态展开策略结合，实现了单个模型同时处理不同加速因子的多任务问题. ...

... ISTA是一种用于稀疏优化问题的迭代算法^[16]，已用于实现CS-MRI重建.当正则化用某个线性稀疏变换P域的L₁范数表示时，基于(1)式的CS-MRI的优化表达式为： ...

... 经过大量对比实验发现，随着网络级联（迭代）数增加，网络学习能力增强，重建图像更优.当级联数大于9时，网络性能的改善并不明显.考虑到网络复杂度、学习参数量及训练时间，将网络级联数设为9.ESPIRiT算法是多线圈CS-MRI传统重建算法的标杆^[24]，可采用小波变换的L₁范数作为正则化项（即：L1-ESPIRiT）.为了评估提出的ISTAVS-Net网络的可行性和性能，将其与两种传统算法（L1-ESPIRiT、ISTA^[16]）和三种深度学习网络（端到端U-Net网络^[23]、ISTA-Net+网络^[17]、VS-Net网络^[19]）进行比较. ...

ISTA-Net: Interpretable optimization-inspired deep network for image compressive sensing

2018

ISTA-NET++: Flexible deep unfolding network for compressive sensing

2021

VS-Net: variable splitting network for accelerated parallel MRI reconstruction

2019

... 变量拆分（分裂）网络（Variable Splitting Network，VS-Net）^[19]通过引入辅助变量，将原变量拆分成多个变量，使计算更加高效.VS-Net通过不同的网络模块来对应迭代步骤，网络结构简单，便于端到端训练，但网络训练过程中指标波动较大，迭代次数决定网络的级联数和复杂度，并影响重建图像质量. ...

... 若采用VS-Net网络的变量拆分法^[19]，可引入新的辅助变量z和

${{x}_{i}}$

，约束条件

$1x=z$

，是为了将正则化项中的x与数据一致性项中的x分离开.约束条件

$2{{S}_{i}}x={{x}_{i}}$

，

${{x}_{i}}$

为每个线圈的图像，是为了把(3)式中求复杂的单变量x问题转变为求简单的多变量

${{x}_{i}}$

问题.也就是从多线圈采集数据

${{y}_{i}}$

逐一恢复多线圈的重建图像

${{x}_{i}}$

，物理含义更加直接简单. ...

Compressed sensing MRI: A review from signal processing perspective

2019

... 香农定理要求采样频率必须大于信号最高频率的2倍，而CS-MRI技术突破了该定理的限制，可以从远低于采样频率的欠采样

$k$

空间数据中，利用图像在变换域中具有稀疏性的先验知识，采用优化理论算法来恢复图像^[20]．CS-MRI成像模型可表示为： ...

A review and experimental evaluation of deep learning methods for MRI reconstruction

2022

... 其中，

$y\in {{C}^{m}}$

为测量值，表示欠采样的空间数据（

$m\ll n$

）；

$x\in {{C}^{n}}$

为待重建的MRI图像；

$A\in {{C}^{m\times n}}$

为测量矩阵；

$\varepsilon$

为采样噪声.CS-MRI在工程上更适合以伪随机减少相位编码行来加快扫描，可使用欠采样掩膜

$D\in {{C}^{(m\times n)}}$

来表达^[21].

$A=DF$

是傅里叶欠采样算子，F表示傅里叶变换. ...

Compressed sensing in sodium magnetic resonance imaging: techniques, applications, and future prospects

2022

... 其中，

$\left\| DFx-y \right\|_{2}^{2}$

表示数据一致性项，

$R(x)$

为正则化项，

$\lambda$

为正则化权重.用正则化项来表示某个域的稀疏性，通常可对图像x求全变分，或对x进行小波变换后取L₁范数，或二者皆有^[22].(3)式是从多个线圈的采集数据

${{y}_{i}}$

中恢复一幅重建图像x，物理含义不够直接. ...

FastMRI: an open dataset and benchmarks for accelerated MRI

... 对重建图像质量的评价采用MRI重建领域常用的3个指标^[23]，归一化均方误差（Normalized Mean Square Error，NMSE）、峰值信噪比（Peak Signal-To-Noise Ratio，PSNR）和结构相似性（Structure Similarity Index Measurement，SSIM），且所有指标均采用测试数据的指标平均值来表示.指标计算的公式分别为： ...

ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA

2014

Dual-domain accelerated MRI reconstruction using transformers with learning-based undersampling

2023

... 当加速因子过高时（AF=8），虽然网络评价指标值较好，但图像伪影并不能完全消除，会影响临床诊断.后续可重新设计加速扫描方式、结合双域加速^[25]等手段来优化网络，以获得更优的重建图像.总之，使用深度学习网络的方法实现MRI重建还存在许多问题尚未解决，离临床落地还有较远的路要走. ...

〈

〉