引言
电子顺磁共振(Electron Paramagnetic Resonance,EPR)谱仪可以对含有未成对电子的物质进行检测,是一种重要的物质结构分析仪器.EPR谱仪被广泛用于化学反应机理研究、生物分子结构分析、材料缺陷和掺杂物的检测等[1⇓⇓⇓⇓-6].近年来太赫兹微波技术[7]与超导磁体技术[8]的进步为高频高场EPR谱仪的发展提供了技术基础.高频高场EPR谱仪相比于传统X波段谱仪具有更高灵敏度、更高谱线分辨率、更大激发能量等优势[9,10],例如利用高频高场EPR谱仪对粉末状酶氨酸缺失的铜蓝蛋白Azurin突变体(AzC-W48)中色氨酸自由基[11]或辅酶Q10阴离子自由基[12]进行探测,可分析自由基的朗德因子张量取向,而这在分辨率较低的X波段谱仪上是难以开展的.
探头是EPR谱仪的核心部件之一,其性能对谱仪的灵敏度、分辨率等指标具有重要影响.待测样品被装载于探头中,磁体系统在探头处产生特定强度的外磁场,微波信号在探头的样品区域被转换为垂直于外磁场的交变磁场,样品中的自旋与外磁场和交变磁场产生相互作用.当满足磁共振条件时,样品会吸收或者辐射出电磁波信号,该信号经由探头传输至微波接收机,再经由一系列信号处理过程转换为最终的谱线.EPR探头有谐振型和非谐振型两类.一种常见的非谐振型探头结构是共面波导[13].相比于谐振型探头,非谐振探头具有更大的工作带宽,但是其探测灵敏度不足.为了提高探测灵敏度,通常选用谐振型探头.常见的谐振型探头包括矩形谐振腔[14]、圆柱形谐振腔[15]、裂环式谐振腔[16]等,其中圆柱形谐振腔在X波段到W波段等谱仪上均有应用.然而当EPR谱仪工作频率达到几十GHz乃至百GHz量级时,圆柱形谐振腔这类封闭式腔体的尺寸会迅速减小,导致腔体的加工难度变大,有效装载样品空间变小,且封闭腔内的样品难以与射频场、光、电场等外部激励耦合,这制约了高频高场EPR谱仪的性能.法布里-珀罗谐振腔(Fabry-Perot Cavity)是一类开放式谐振腔,相比于圆柱形谐振腔更容易与外部场实现耦合[17,18],且其谐振结构和较大的样品装载空间保证了高灵敏度.在1985年,Haindl等人[19]开发出首台基于法布里-珀罗谐振腔的W波段EPR谱仪.接着在2005年Earle等人[20]利用基于法布里-珀罗谐振腔的EPR谱仪实现了对生物溶液样品的测试.2010年,Neugebauer研发了基于法布里-珀罗谐振腔的宽带EPR谱仪[21].目前国内尚缺少基于法布里-珀罗谐振腔的高频高场EPR设备的研制.
1 探头设计
图1
从法布里-珀罗谐振腔反射出的信号功率
法布里-珀罗谐振腔的空载品质因数为
图2
图2
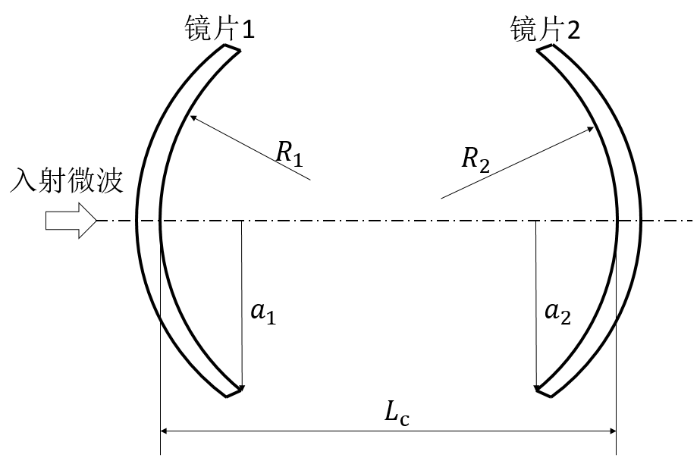
(a)探头的结构示意图, 探头主要由法布里-珀罗谐振腔与波纹波导构成, 波纹波导将入射的TE11模式的微波转化为HE11模式,①~④表示波导的各分段;(b)波纹波导②的剖面图;(c)法布里-珀罗谐振腔的结构示意图,⑤金属网格和⑥球面镜构成谐振腔结构;(d)探头实物图,核心部件包括:⑦金属网格、⑧样品台、⑨调制场线圈、⑩球面镜、⑪⑫⑬压电位移台
Fig. 2
(a) Schematic diagram of the probe, mainly composed of two parts, Fabry-Perot cavity and corrugated waveguides. The corrugated waveguides work as a mode converter for generating the HE11 mode from the TE11
如图2(b)所示,波纹波导的内壁上分布有周期性的波纹.波纹的参数包括波纹深度d、波纹周期p、波纹宽度
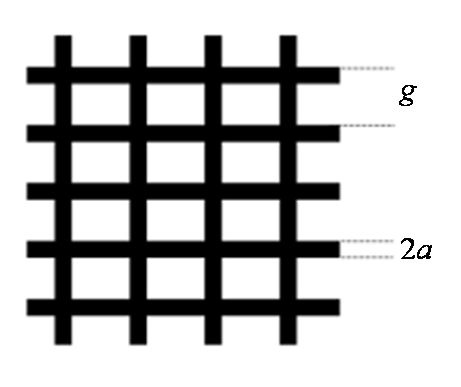
如图2(c)所示,法布里-珀罗谐振腔主要由金属网格和一个球面镜组成.入射微波激发了金属网格表面等离子激元,表面等离子激元部分能量耦合到网格结构的另一面再耦合成微波出射,部分能量从入射面反射,因此金属网格的设计能耦合一部分入射的微波到法布里-珀罗谐振腔内,同时能够将谐振腔的功率耦合一部分到外部的微波传输线.可以通过调节金属网格的参数来调节金属网格对特定频段微波的透射率和反射率[27].当微波频率与谐振腔谐振频率相同时,入射微波在金属网格和球面镜之间多次反射,形成高斯模式的驻波.金属网格可以减少由于模式不匹配、模式转化或空间辐射导致的能量损耗[28],我们选择如图3所示的正方形金属网格作为耦合结构,金属条纹的宽度2a=40 μm,网格周期g=200 μm.金属网格对微波的反射与透射能力受金属网格尺寸参数的控制:2a=g时,金属网格为全封闭结构,入射微波近乎完全反射;当2a=0时,金属网格为全开放结构,此时入射微波近乎完全透射;当0<2a<g时,金属网格具有一定的反射和透射能力.本文设计的金属网格是在中国科学技术大学微纳研究与制造中心制成的,在直径为28 mm、厚度为0.26 mm的圆柱形双抛石英片上通过金属电镀工艺先镀一层200 nm的钛膜以增加金属的附着能力,再镀一层2 000 nm的铜膜,然后通过掩模版方法剥去金属膜中不需要的部分,最终得到目标金属网格.
图3
图3
金属网格示意图. 黑色条纹为金属条纹
Fig. 3
Scheme of the metallic mesh. The black areas are metallic strips
金属网格的反射与透射能力取决于网格的参数,反射率
其中归一化阻值
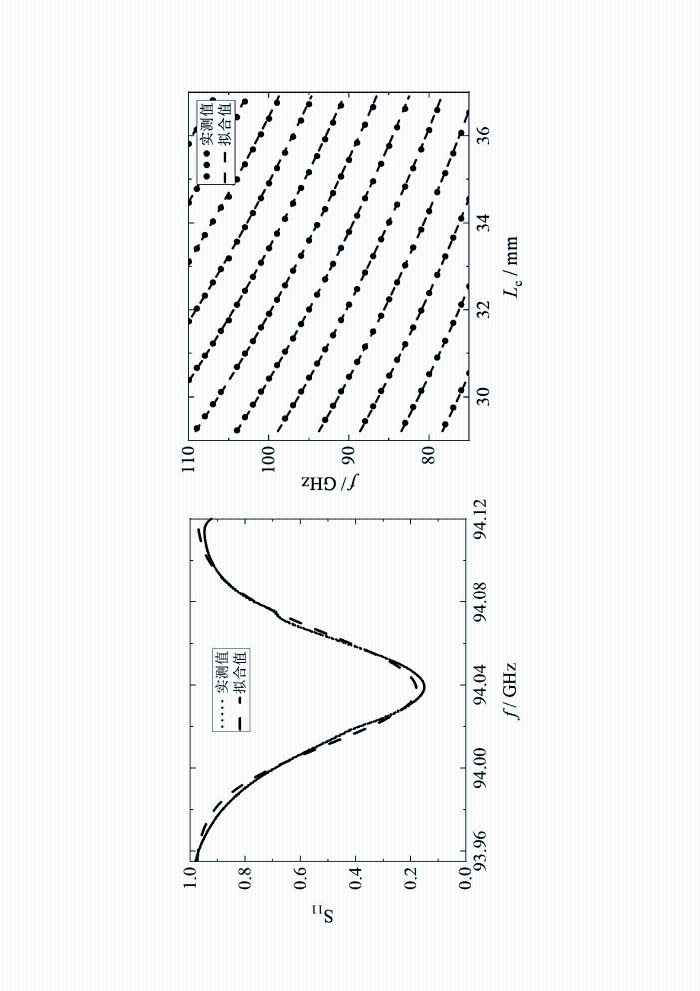
按照图2(d)所示结构组装探头,在探头顶部连接矢量网络分析仪的微波端口,通过直线位移台调节法布里-珀罗谐振腔的腔长度来控制法布里-珀罗谐振腔的谐振状态,记录法布里-珀罗谐振腔谐振时的反射曲线与非谐振时的反射曲线,将两次记录的反射曲线作差得到探头的反射曲线.实验测得探头的反射曲线如图4(a)实测值所示,使用公式
图4
图4
(a)探头反射曲线的测试结果和拟合结果. 其中黑色点为实测数据,虚线为拟合结果. (b)不同直线位移台移动长度下法布里-珀罗谐振腔谐振频率的测试结果和拟合结果. 其中黑色点为实测数据,虚线为拟合结果
Fig. 4
(a) Reflection coefficient of the probe. Black dots are experimental data, and the dashed line stands for the fitting result. (b) Resonance frequency of the Fabry-Perot cavity versus the moving distance of the piezoelectric positioner. Black dots are experimental data, and the dashed lines stand for the fitting result
2 装载法布里-珀罗谐振腔探头的EPR谱仪性能测试
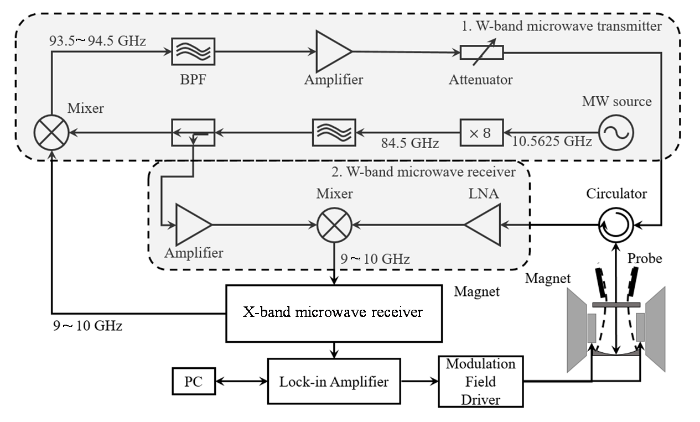
将法布里-珀罗谐振腔探头安装到W波段EPR谱仪,进行连续波EPR实验.谱仪结构如图5所示,主要包括超导磁体(Magnet)、X波段微波桥(X-band microwave bridge)、W波段发射机(W-band microwave transmitter)、W波段接收机(W-band microwave receiver)、探头(Probe)、控制与读出系统(PC).超导磁体在样品处产生的磁场为水平方向,场强范围是
图5
图5
W波段顺磁共振谱仪结构图[30]. 超导磁体生成B0场. 矩形框1为W波段发射机. 线路中84.5 GHz的本振微波信号与9~10 GHz的信号混频,生成93.5~94.5 GHz的W波段微波. 矩形框2为W波段接收机,探头出射的信号经过低噪声放大器后与84.5 GHz的本振信号混频,得到X波段信号进入X波段微波桥,经锁相放大器检测转换为数字信号
Fig. 5
Schematic diagram of the W-band EPR spectrometer. The superconducting magnet generates
2.1 探头调制场幅度标定实验
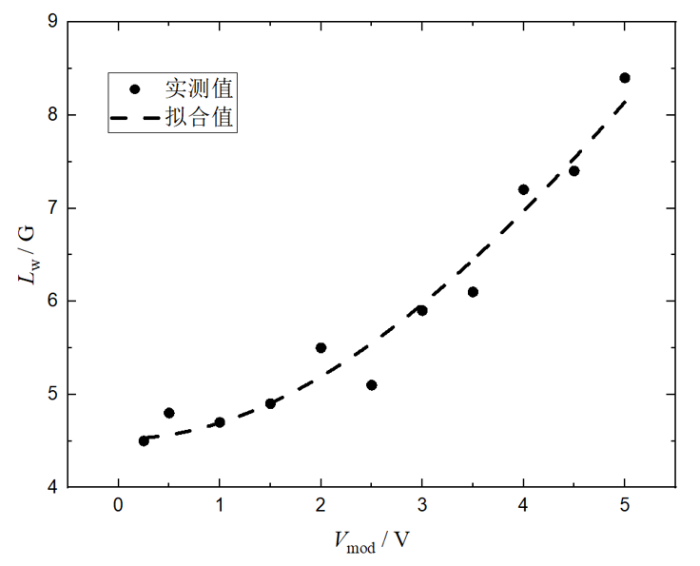
连续波EPR谱仪使用调制场技术来提高谱线信噪比(Signal-to-Noise Ratio,SNR),调制场幅度的准确性对于谱线分析至关重要,因此需要对调制场幅度进行标定.通过分析不同调制场驱动电压下谱线的线宽来对调制场幅度进行标定.连续波EPR谱线一阶微分谱的实测线宽
其中
实验中使用Mn标样品测试其常温下的W波段连续波EPR谱线,使用上述方法进行调制场幅度的标定.微波功率设定为2.8 mW,调制场线圈驱动电压在0.25~5.00 V区间内取11个点,所得一阶微分谱实测线宽
图6
图6
不同调制场幅度下Mn标样品的W波段EPR谱线一阶微分谱线宽测试结果,其中黑色点为实测数据,虚线为拟合结果
Fig. 6
W-band continuous wave EPR linewidth of Mn(II) measured at different modulation voltage. Black dots are experimental data, and the dashed line stands for the fitting result
2.2 灵敏度评估
使用上述Mn标样品测试谱仪绝对自旋数灵敏度.谱仪绝对自旋数灵敏度通过最小可测量自旋数来评估,最小可测量自旋数代表谱线信噪比为1时对应的样品自旋数目,该值越小谱仪性能越好.对于占据特定空间大小的Mn标样品,连续波EPR一阶微分谱线的信噪比表达式如(5)式所示[32]:
其中
对于占据特定空间大小的样品,
选用Mn标样品进行连续波信号测试.Mn标样品的等效哈密顿量为[33]:
(8)式中{{g}_{\text{e}}}表示电子自旋的朗德因子,{{\mu }_{\text{e}}}表示波尔磁子, {{g}_{\text{n}}}表示Mn(II)核自旋的朗德因子, {{\mu }_{\text{n}}}表示核磁子,B表示外磁场大小, S表示电子自旋,I表示核自旋, A表示超精细耦合常数.Mn标样品占据主导的跃迁谱线为|+\frac{1}{2}, {{m}_{I}}\rangle \leftrightarrow |-\frac{1}{2}, {{m}_{I}}\rangle , {{m}_{I}}=\pm \frac{1}{2}, \pm \frac{3}{2},\pm \frac{5}{2}, 跃迁能量为\Delta E(|+\frac{1}{2}, {{m}_{I}}\rangle \leftrightarrow |-\frac{1}{2},{{m}_{I}}\rangle )={{g}_{\text{e}}}{{\mu }_{\text{e}}}B+A{{m}_{I}}. {{m}_{I}}的不同取值分别对应不同EPR吸收峰,总共六个峰.Mn标样品装载于内径为0.5 mm的样品管内,样品高度为7.12 mm, 总体积为{{V}_{\text{Mn}}}=1.4\text{ m}{{\text{m}}^{\text{3}}}, 该样品的自旋浓度为1.1\times {{10}^{12}}\text{ m}{{\text{m}}^{-3}}, 得总自旋数为{{N}_{\text{S}}}=1.6\times {{10}^{12}}.
表1 EPR实验参数
Table 1
| 名称 | 参数 |
|---|---|
| 样品 | Mn标样品 |
| 温度 | 室温 |
| 微波功率 | 2.8 mW |
| 时间常数 | 100 ms |
| 调制场频率 | 100 kHz |
| 调制场幅度 | 4.4 G |
| 扫场范围 | 3.31~3.38 T |
| 扫描点数 | 1750 |
图7
图7
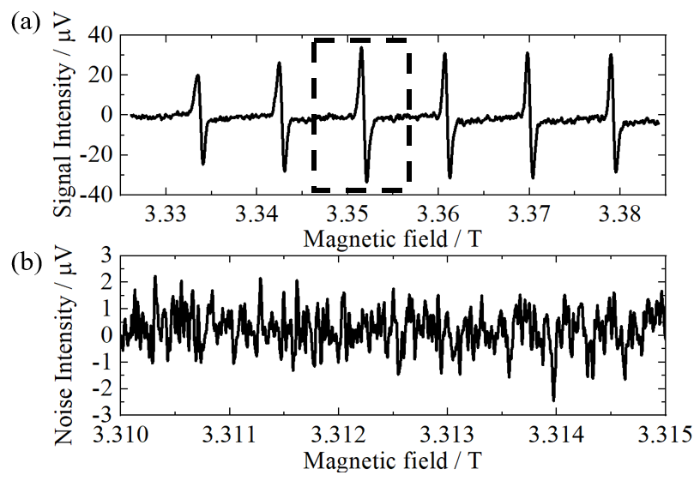
(a)常温下Mn标样品的W波段连续波EPR谱线. 测试虚线框内信号的峰峰值作为信号强度. (b)磁场偏共振下的噪声谱. 微波频率为94.04 GHz,微波功率为2.8 mW,调制场幅度为4.4 G@100 kHz,时间常数为100 ms
Fig. 7
(a) W-band continuous wave EPR spectra of Mn(II) in GaO powder at room temperature. The peak to peak amplitude of the signal within the dashed box is measured as the signal strength. (b) Noise signal measured at off resonance. The MW frequency is 94.04 GHz with an input power of 2.8 mW. The modulation amplitude is 4.4 G@100 kHz. The time constant is 100 ms
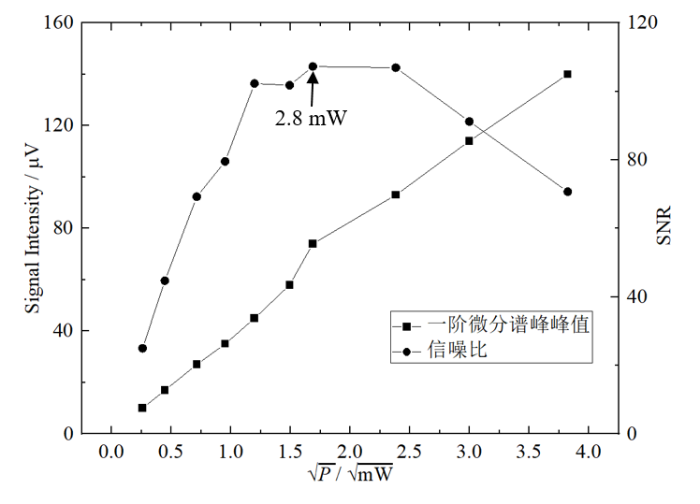
通过改变微波功率(0.067~15 mW),其他测试参数同表1,测试了一系列不同微波功率下Mn标样品EPR谱红色虚线框内对应峰的信号强度和磁场偏共振时的噪声信号大小,测试结果如图8所示.从图8中可见,微波功率小于2.8 mW时信号强度与信噪比都随微波功率的增加而增加,当微波功率大于2.8 mW时信号强度随微波功率的增加而增加,但是信噪比随微波功率的增加而减小,微波功率为2.8 mW时信噪比达到最大值(99),通过(7)式得常温下谱仪绝对自旋数灵敏度为6.6×108 spins/(G•
图8
图8
不同样品微波功率下Mn标样品的W波段EPR谱线一阶微分谱峰峰值与信噪比的测试结果
Fig. 8
W-band continuous wave EPR signal intensity and SNR of Mn(II) measured at different microwave power
将国际上已发表的代表性高频EPR谱仪灵敏度与本工作进行比较,结果见表2.序号1、2和3的谱仪分别使用了圆柱形谐振腔、法布里-珀罗谐振腔和非谐振型探头.由于仪器的灵敏度数据在不同温度下测得,为了合理比较需将灵敏度修正为室温灵敏度.根据电子自旋的极化度来修正信号强度,电子自旋的极化度
表2 本文工作与现有EPR谱仪对比
Table 2
| 序号 | 频率/GHz | 探头种类 | 灵敏度/ (spins/(G• | 极化度 | 室温灵敏度/ (spins/(G• |
|---|---|---|---|---|---|
| 1[34] | 94 | 圆柱形谐振腔 | 0.7515% | ||
| 2[22] | 95 | 法布里-珀罗谐振腔 | 1.753% | ||
| 3[35] | 94 | 非谐振 | 90.57% | ||
| 4(本工作) | 94 | 法布里-珀罗谐振腔 | 0.7515% |
谱仪1使用了具有高品质因数和高填充系数的圆柱形谐振腔,其灵敏度是这四台谱仪中的最优灵敏度.本工作与使用了法布里-珀罗谐振腔的谱仪2灵敏度相当,远优于使用了非谐振结构探头的谱仪3的灵敏度.通过典型尺寸评估谐振腔的体积,对于谱仪1的TE011模式的圆柱形谐振腔,圆柱底面半径为
3 结论
本文设计了一款基于法布里-珀罗谐振腔的W波段EPR谱仪探头,探头主要包括法布里-珀罗谐振腔及波纹波导.该探头能够在W波段工作,空载品质因数为1 542,由于在样品台附近的笼式结构支撑长杆上预留了空间,可以方便的实现与外部场的耦合.使用Mn标样品进行常温下W波段连续波EPR实验,标定得到装载该探头的EPR谱仪绝对自旋数灵敏度为6.6×108 spins/(G•
装载该探头的EPR谱仪所测得的EPR谱线线宽偏大,这源于黄铜材料的波纹波导退火处理后剩磁仍然过大导致磁场均匀性有限,这在一定程度限制了EPR谱仪性能.下一步工作将对腔体附近的机械结构和材料进行优化,利用紫铜材料制作波导并减少波导侧壁厚度以减少波导的剩磁,来提高磁场的均匀性.同时基于该探头开展脉冲EPR实验,并集成电子-核双共振功能、光照功能等,发挥法布里-珀罗腔的优势,将W波段EPR谱仪应用于金属蛋白分析、生物分子结构解析、量子计算等研究方向.
利益冲突
无
参考文献
High-field EPR spectroscopy applied to biological systems: characterization of molecular switches for electron and ion transfer
[J].The last decade witnessed a tremendous growth in combined efforts of biologists, chemists and physicists to understand the dominant factors determining the specificity and directionality of transmembrane transfer processes in proteins. A large variety of experimental techniques is being used including X-ray and neutron diffraction, but also time-resolved optical, infrared and magnetic resonance spectroscopy. This is done in conjunction with genetic engineering strategies to construct site-specific mutants for controlled modification of the proteins. As a general perception of these efforts, the substantial influence of weak interactions within the protein and its membrane interfaces is recognized. The weak interactions are subject to subtle changes during the reaction cycle owing to the inherent flexibility of the protein-membrane complex. Specific conformational changes accomplish molecular-switch functions for the transfer process to proceed with optimum efficiency. Characteristic examples of time varying non-bonded interactions are specific H-patterns and/or polarity effects of the microenvironment. The present perception has emerged from the coupling of newly developed spectroscopic techniques - and advanced EPR certainly deserves credit in this respect - with newly developed computational strategies to interpret the experimental data in terms of protein structure and dynamics. By now, the partners of this coupling, particularly high-field EPR spectroscopy and DFT-based quantum theory, have reached a level of sophistication that applications to large biocomplexes are within reach. In this review, a few large paradigm biosystems are surveyed which were explored lately in our laboratory. Taking advantage of the improved spectral and temporal resolution of high-frequency/high-field EPR at 95 GHz/3.4 T and 360 GHz/12.9 T, as compared to conventional X-band EPR (9.5 GHz/0.34 T), three biosystems are characterized with respect to structure and dynamics: (1) Light-induced electron-transfer intermediates in wild-type and mutant reaction-centre proteins from the photosynthetic bacterium Rhodobacter sphaeroides, (2) light-driven proton-transfer intermediates of site-specifically nitroxide spin-labelled mutants of bacteriorhodopsin proteins from Halobacterium salinarium, (3) refolding intermediates of site-specifically nitroxide spin-labelled mutants of the channel-forming protein domain of Colicin A bacterial toxin produced in Escherichia coli. The detailed information obtained is complementary to that of protein crystallography, solid-state NMR, infrared and optical spectroscopy techniques. A unique strength of high-field EPR is particularly noteworthy: it can provide highly desired detailed information on transient intermediates of proteins in biological action. They can be observed and characterized while staying in their working states on biologically relevant time scales. The review introduces the audience to origins and basic experiments of EPR in relation to NMR, describes the underlying strategies for extending conventional EPR to high-field/high-frequency EPR, and highlights those details of molecular information that are obtained from high-field EPR in conjunction with genetic engineering and that are not accessible by "classical" spectroscopy. The importance of quantum-chemical interpretation of the experimental data by DFT and advanced semiempirical molecular-orbital theory is emphasized. A short description of the laboratory-built 95 GHz and 360 GHz EPR/ENDOR spectrometers at FU Berlin is also presented. The review concludes with an outlook to future opportunities and challenges of advanced bio-EPR in interdisciplinary research.
EPR-aided approach for solution structure determination of large RNAs or protein-RNA complexes
[J].
Principles and applications of EPR spectroscopy in the chemical sciences
[J].
DOI:10.1039/c6cs00565a
PMID:29498718
[本文引用: 1]

Electron spins permeate every aspect of science and influence numerous chemical processes: they underpin transition metal chemistry and biochemistry, mediate photosynthesis and photovoltaics and are paramount in the field of quantum information, to name but a few. Electron paramagnetic resonance (EPR) spectroscopy detects unpaired electrons and provides detailed information on structure and bonding of paramagnetic species. In this tutorial review, aimed at non-specialists, we provide a theoretical framework and examples to illustrate the vast scope of the technique in chemical research. Case studies were chosen to exemplify systematically the different interactions that characterize a paramagnetic centre and to illustrate how EPR spectroscopy may be used to derive chemical information.
Non-Kramers iron S = 2 ions in β-Ga2O3 crystals: high-frequency low-temperature EPR study
[J].
Reduction of surface spin-induced electron spin relaxations in nanodiamonds
[J].
Design and performance of a new multifunction X-band EPR spectrometer
[J].
新型X波段多功能EPR谱仪的设计与性能
[J].
DOI:10.11938/cjmr20212965
[本文引用: 1]

本文设计和研制了一款新型X波段多功能电子顺磁共振(electron paramagnetic resonance,EPR)谱仪,并为其开发一款新的控制和读出系统(control and readout system,CRS)来操控微波脉冲的产生和信号的采集,提高了系统的集成度和可扩展性. 该谱仪可实现常规的连续波EPR(continuous-wave EPR,cw-EPR)、脉冲EPR(pulsed EPR)和瞬态EPR(transient EPR,trEPR)实验,并装配了6~300 K的无液氦变温装置,以及兼具平行模式与垂直模式的新型双模连续波谐振腔和用于脉冲EPR及trEPR的介质腔. 针对新型EPR谱仪和新谐振腔,本文利用双模连续波、脉冲和瞬态三个不同方式的EPR实验,对其功能进行了验证.
Design and optimization of terahertz directional coupler based on hybrid-cladding hollow waveguide with low confinement loss
[J].
Conductors for commercial MRI magnets beyond NbTi: requirements and challenges
[J].
Sensitivity considerations in microwave paramagnetic resonance absorption techniques
[J].
High-field/high-frequency EPR spectroscopy in protein research: principles and examples
[J].
High-frequency and high-field electron paramagnetic resonance (HFEPR): a new spectroscopic tool for bioinorganic chemistry
[J].
DOI:10.1007/s00775-013-1084-3
PMID:24477944
[本文引用: 1]

This minireview describes high-frequency and high-field electron paramagnetic resonance (HFEPR) spectroscopy in the context of its application to bioinorganic chemistry, specifically to metalloproteins and model compounds. HFEPR is defined as frequencies above ~100 GHz (i.e., above W-band) and a resonant field reaching 25 T and above. The ability of HFEPR to provide high-resolution determination of g values of S = 1/2 is shown; however, the main aim of the minireview is to demonstrate how HFEPR can extract spin Hamiltonian parameters [zero-field splitting (zfs) and g values] for species with S > 1/2 with an accuracy and precision unrivalled by other physical methods. Background theory on the nature of zfs in S = 1, 3/2, 2, and 5/2 systems is presented, along with selected examples of HFEPR spectroscopy of each that are relevant to bioinorganic chemistry. The minireview also provides some suggestions of specific systems in bioinorganic chemistry where HFEPR could be rewardingly applied, in the hope of inspiring workers in this area.
Pulsed ENDOR at 95 GHz on the primary acceptor ubisemiquinone in photosynthetic bacterial reaction centers and related model systems
[J].
Optimization of coplanar waveguide resonators for ESR studies on metals
[C]//
Quantitative interpretation of multifrequency multimode EPR spectra of metal containing proteins, enzymes, and biomimetic complexes[M]// Methods in Enzymology
Cavity-and waveguide-resonators in electron paramagnetic resonance, nuclear magnetic resonance, and magnetic resonance imaging
[J].
Quasioptical hardware for a flexible FIR-EPR spectrometer
[J].
High-field/high-frequency EPR/ENDOR—a powerful new tool in photosynthesis research
[J].
A 94 GHz EPR spectrometer with Fabry-Perot resonator
[J].
High-frequency ESR at ACERT
[J].
A novel high-field/high-frequency EPR and ENDOR spectrometer operating at 3 mm wavelength
[J].
Radiation patterns of the HE11 mode and Gaussian approximations
[J].
Quasi-optical CW mm-wave electron spin resonance spectrometer
[J].
Low-loss broadband multimode corrugated waveguide performance
[J].
Gaussian-beam open resonator with highly reflective circular coupling regions
[J].
Far-infrared properties of metallic mesh and its complementary structure
[J].
A design of resonant cavity with an improved coupling-adjusting mechanism for the W-band EPR spectrometer
[J].
The effect of field modulation on a simple resonance line shape
[J].
EPR of Mn (II) complexes with enzymes and other proteins
[J].
The Bruker high-frequency-EPR system
[J].
Capabilities of compact high-frequency EPR/ESE/ODMR spectrometers based on a series of microwave bridges and a cryogen-free magneto-optical cryostat
[J].