引言
高极化率、高密度极化3He气体的研究在过去二三十年内取得了非常快速的进展,其在科学研究、医学诊断、精密测量等多领域有着十分广泛的应用.在科学研究方面,极化3He中子极化技术是目前已知的最先进的极化中子技术[1⇓⇓-4];在医学诊断方面,使用极化的惰性气体作为造影剂可增强磁共振成像信号,提高医学诊断的准确度[5⇓⇓-8];基于极化惰性气体的量子陀螺仪可以实现高精度导航,同样基于该技术的量子磁强计可用于高精度磁异常探测从而实现军事或民用用途[9,10];此外,惰性气体极化原子核技术作为一种精密测量的手段还可用于探测标准模型之外的新物理和新相互作用,这将有助于解决基础物理学里目前最重要的问题——暗物质暗能量问题以及量子色动力学里的强CP问题[11⇓⇓⇓-15]等等.
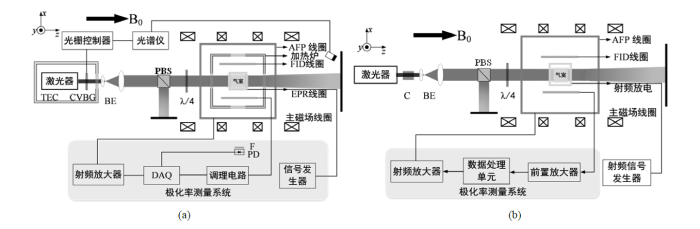
自旋交换光泵浦(Spin-Exchange Optical Pumping,SEOP)和亚稳态交换光泵浦(Metastable-Exchange Optical Pumping,MEOP)技术是极化3He领域常用的两种极化3He原子的方法[3].SEOP技术通过特定波长的激光极化碱金属铷或钾的外层电子,再通过自旋交换碰撞和超精细相互作用将角动量传递给3He原子的原子核.与SEOP技术不同的是,MEOP技术通过红外激光使亚稳态3He原子获得极化,再通过亚稳态交换碰撞(Metastable-Exchange Collisions,MECs)将角动量传递给3He原子的原子核.不论采用何种极化技术,3He极化系统都应包含主磁场系统、光泵浦系统和极化率测量系统,3He极化系统示意图如图1所示.主磁场系统提供恒定的轴向磁场,使3He原子的能级产生劈裂从而出现超精细能级;光泵浦系统为原子气室提供特定波长的圆偏振光,实现原子能级的布居数反转,从而形成原子极化;极化率测量系统通过核磁共振(Nuclear Magnetic Resonance,NMR)技术或基于法拉第旋转原理测量3He原子的极化率,从而确定原子的极化状态.
图1
图1
3He极化系统示意图. (a)基于SEOP极化技术的系统;(b)基于MEOP极化技术的系统. 其中,TEC:温度控制装置;CVBG:啁啾体布拉格光栅;BE:扩束器;PBS:偏振分束立方;F:滤光片;PD:光电探头;C:准直器
Fig. 1
Schematic diagram of the polarized 3He system. (a) System based on the SEOP polarization technique; (b) system based on the MEOP polarization technique. TEC: temperature control device, CVBG: chirped volume Bragg grating, BE: beam expander, PBS: polarizing beam splitter cube, F: filter, PD: photodetector, C: collimator
极化率的精确测量对于3He极化系统而言至关重要,NMR技术是极化率测量中常用的方法[2,3,16].对于SEOP极化系统而言,测量极化率通常使用绝热快速通道(Adiabatic Fast Passage,AFP)NMR技术和自由震荡衰减(Free Induction Decay,FID)NMR技术;对于MEOP极化系统而言,通常使用激光探测技术和FID NMR技术.FID NMR技术无疑是3He极化系统极化率实时监测时最为常用的技术,它通过一组线圈在y轴方向上施加一段时间的单频激励信号,此时3He原子的核磁矩会逐渐偏离z轴方向,当激励信号消失后,原子核磁矩从当前位置逐渐恢复到初始状态,这个过程中核磁矩的横向分量Mxy会逐渐减小,在x轴方向上的线圈中将会产生一个感应电压信号,被称为FID信号.该技术基于电磁感应原理,结构简单,易于实现.FID NMR线圈是该技术的核心,其探测灵敏度与线圈的设计参数(半径、匝数、线径等)、线圈与3He原子气室的距离、3He磁化矢量偏转的角度以及系统噪声等多个因素有关.其设计一直是该领域十分关注的问题之一,参考文献[17⇓~19]都对该线圈的SNR模型进行了理论分析,但遗憾的是均未进行实验验证.
1 实验部分
1.1 实验原理分析
FID线圈通常为一个或一对放置于气室周围的空心线圈,在一些世界知名实验室(如美国杜克大学、美国国家标准局、美国印第安纳大学等)使用的3He极化装置中,拾波线圈大多都是半径1 cm左右,匝数100左右的小线圈[19],其电路的等效模型可看作一个RLC回路.对于FID线圈的优化工作就是求解线圈直径、气室直径、线圈与气室之间的距离等因素与探测信噪比之间的关系,测量得到的信号即是FID信号,而测量的噪声则由多部分组成.
1.1.1 FID线圈的测量信号
首先对线圈中感应到的FID信号进行分析,气室与线圈的相对位置如图2所示.
图2
图2
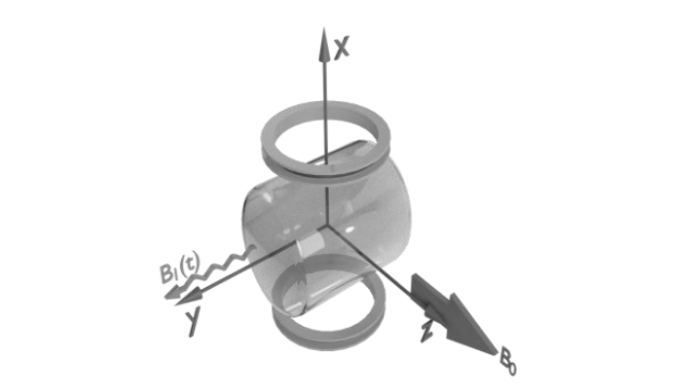
圆柱形原子气室与线圈位置示意图.FID线圈对称地放置于柱面两侧,射频信号作用于y轴方向,泵浦光方向和主磁场方向均与z轴平行
Fig. 2
The schematic diagram represents the position of the cylindrical atomic chamber and the coils. The FID coils are symmetrically placed on both sides of the cylindrical surface. The RF signal is applied in the direction of the y-axis, and the direction of the pumping light and the main magnetic field are both parallel to the z-axis
在3He极化系统中,泵浦激光与主磁场方向保持一致,这致使原子角动量的初始方向沿着z轴,此时沿z方向存在一个初始磁化强度M.FID信号的探测采用NMR技术,利用一个持续时间为τ的射频(Radio Frequency,RF)信号从垂直于主磁场方向作用于3He原子,此时核磁矩会偏离z轴一个角度,当撤掉该信号且其频率接近于3He原子核在主磁场中的拉莫尔进动频率时,在x方向上核磁矩的进动信号可表示为[18]:
其中,δ为射频磁场引起的原子角动量偏转的初始角度,T2为横向弛豫时间,
由气室内的原子磁矩在周围空间产生的磁场可通过求解分布在柱形气室表面的有效磁荷所产生的标量势的梯度来计算.在柱坐标系中,以
其中,Φ为磁通量,
根据法拉第电磁感应定律,线圈中感应电动势可表示为:
其中,n为线圈匝数,B为磁感应强度,S为线圈面积.结合(2)式和(3)式,使用数值计算的方法可以得到柱形气室在线圈中产生的FID信号的幅值.为了理论分析方便,本文使用球形气室模型模拟柱形气室产生的FID信号,球形气室的FID信号有解析表达式[18]:
其中,N为FID线圈匝数,rcoil、rcell分别为线圈和气室的半径,d为线圈中心到气室表面的距离.由于本文旨在分析FID线圈的优化设计,因此仅考虑(4)式中与线圈、气室物理尺寸相关的部分,即:
1.1.2 FID线圈的等效噪声模型
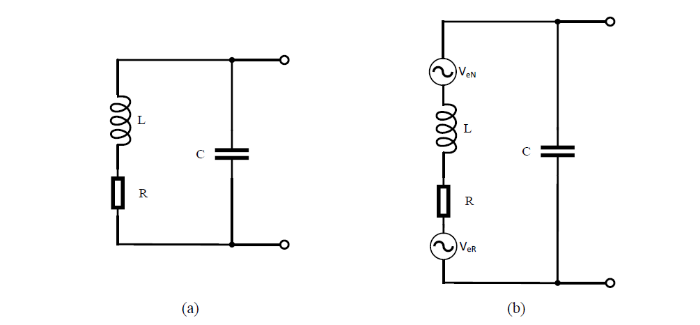
测量噪声源主要由以下几部分构成:FID线圈的电阻热噪声、环境磁场引起的感应电压噪声以及测试电路引入的噪声,对于不同的线圈而言,其测量电路是一致的,因此将该部分作为一个常数.FID线圈的等效电路模型及噪声模型如图3所示.
图3
图3
(a) FID线圈的等效电路模型;(b) FID线圈的等效噪声模型
Fig. 3
(a) The equivalent circuit model of the FID coil; (b) the equivalent noise model of the FID coil
VeN和VeR分别表示线圈感应到的环境磁噪声和线圈电阻的热噪声.先考虑线圈电阻的热噪声,当线圈电阻为R时,根据Johnson Noise公式,线圈电阻两端噪声电压的功率谱密度为[22]:
其中k=1.380 649×10-23 J/K为玻尔兹曼常数,T为环境温度.仅考虑电阻的噪声电压时,线圈两端输出电压可表示为:
由于线圈等效电路为RLC电路,存在谐振点,当其工作于谐振频率点时,即
其中Q是线圈的品质因数,
其中Q可由实验测得,
继续考虑由环境磁场引起的感应电压噪声,假设环境电磁噪声的等效功率谱密度为SB(ω),则线圈两端产生的感应电压为:
类似地,带宽内环境噪声的方差可表示为:
由电路叠加定理可得,综合考虑环境噪声和电阻热噪声,由(10)式和(12)式,并对气室直径做归一化,可得测量得到线圈噪声的拟合公式如(13)式所示,其中a、b、c为常数.
1.1.3 信噪比分析
假设拾波线圈的谐振电路频率和进动频率一致,则线圈输出端的电压信号为:
同样地,对气室直径做归一化后线圈测量信噪比可表示为:
(15)式中A、B、C均为拟合参数.其中,A与气室中原子的初始进动条件相关,B与气室半径相关,C与线圈中心到气室的距离相关.
1.2 实验装置
在基于MEOP技术的极化3He系统中,装有超极化3He气体的原子玻璃气室置于主磁场线圈的中心,玻璃气室呈圆柱形,半径为2.5 cm,高度为5 cm,气压为100 Pa.射频线圈对称地放置于气室的上下方,用于产生射频激励信号.FID线圈对称地放置于气室的左右两侧,用于接收3He原子的FID信号.实验装置实物图如图4所示.
图4
本文的实验部分主要验证了FID线圈的直径与探测信噪比的关系,实验设计了8个不同直径的FID线圈,除直径不相同以外,各个线圈的线径(dw = 0.015 mm)、匝数(N = 600)、线圈宽度(l0 = 5 mm)及线圈到气室表面的距离d均相同.根据1.1节的原理分析,实验前需要对FID线圈进行调谐,以确保线圈的谐振频率与3He原子的进动频率相同.不同直径的FID线圈的测量参数如表1所示.
表1 不同直径的FID线圈的测量参数
Table 1
| 内直径/mm | 电阻R/Ω | 电感L/mH | 调谐后线圈的谐振频率/kHz | 品质因数Q | |
|---|---|---|---|---|---|
| 1 | 5 | 15.2 | 0.79 | 34.60 | 10.97 |
| 2 | 10 | 24.8 | 2.14 | 34.93 | 15.63 |
| 3 | 15 | 36.3 | 3.82 | 34.71 | 20.69 |
| 4 | 20 | 43.3 | 5.60 | 34.78 | 25.78 |
| 5 | 25 | 54.9 | 6.88 | 34.73 | 27.91 |
| 6 | 30 | 65 | 9.72 | 34.90 | 29.75 |
| 7 | 49 | 97.9 | 17.27 | 34.82 | 35.21 |
| 8 | 59 | 114.6 | 21.36 | 34.90 | 36.02 |
1.3 实验过程
实验时,调节主磁场B0使3He原子的拉莫尔进动频率接近线圈调谐后的谐振频率.3He原子极化完成后,使用上位机控制数据采集卡(Data Acquisition,DAQ)给RF线圈输出一个瞬时脉冲,当射频脉冲消失后,3He原子开始弛豫,此时采集调谐电容两端电压,该电压经前置放大器放大后输入锁相放大器,同时上位机控制DAQ产生一个同步差频信号作为锁相放大器的参考信号,从而得到输入信号的同相或正交分量.由于FID信号会随时间衰减,因此将该分量幅值的最大值作为FID信号的幅值.
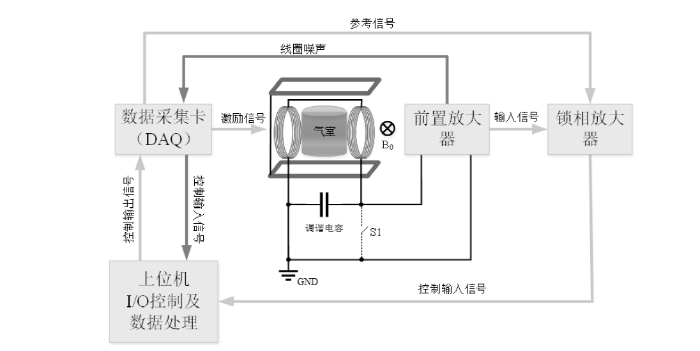
实验过程的示意图如图5所示.噪声测量时,首先将线圈对地短路(闭合S1),使用DAQ采集前置放大器的输出估算仪器的背景噪声.然后断开S1,在不具备3He原子极化时,使用DAQ采集前置放大器的输出时域噪声,通过计算其噪声功率谱得到线圈谐振频率附近的噪声功率谱密度,继而可求得噪声的方差(在指定带宽内的积分),如(10)式和(12)式所示,最后通过计算FID信号的幅值与噪声标准差的比值求得线圈的测量信噪比.这里值得注意的是,尽管信噪比通常而言是功率的比值,但本文旨在分析线圈半径与测量信噪比的关系,因此只需求得信噪比在FID线圈半径改变时的相对变化即可.
图5
2 结果与讨论
2.1 实验结果
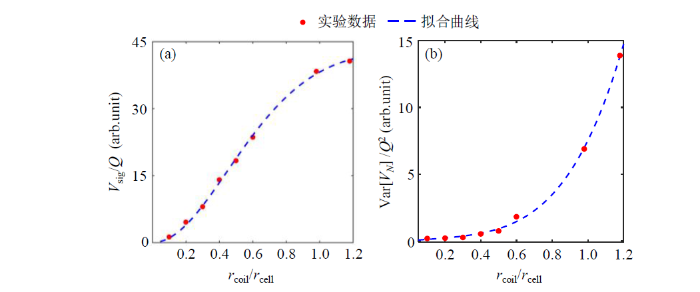
实验对具有不同直径的8组线圈分别进行了FID信号的测量,同时在3He非极化的状态下对噪声进行了测量,取FID信号的幅值与噪声的标准差之比作为线圈SNR的测量结果.使用(5)式和(14)式、(13)式分别对测量得到的FID信号的幅值和噪声进行拟合,拟合结果如图6所示(为了显示方便对纵坐标的值做了放大处理).结果显示公式与实验结果有很好的符合度,其拟合的决定系数(Coefficient of Determination,R2)大于99.8%.
图6
图6
实验结果. (a) FID信号幅值随rcoil/rcell的变化关系;(b)噪声方差随rcoil/rcell的变化关系
Fig. 6
Experimental results. (a) Relationship between FID signal amplitude and rcoil/rcell; (b) relationship between noise variance and rcoil/rcell
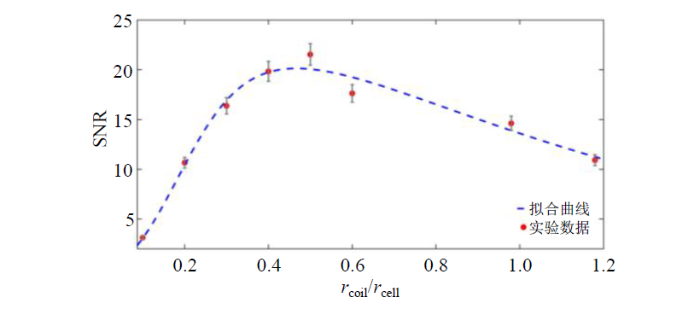
使用(15)式对测量得到的线圈SNR的结果进行拟合,拟合结果如图7所示,其拟合的R2大于97.5%,且拟合结果的相对误差不大于10%.
图7
图7
FID线圈的测量信噪比随rcoil/rcell的变化关系
Fig. 7
Relationship between the measured SNR of FID coil and rcoil/rcell
根据理论分析及实验结果可以得出以下结论:①线圈测量的SNR与线圈的直径、线圈中心到气室表面的距离、磁场环境、3He原子的极化率等多种因素相关;②FID线圈的测量信噪比随rcoil/rcell的变化存在最优值,根据本文的实验结果,线圈的测量SNR在rcoil/rcell=0.5时取得了最大值.
2.2 误差分析
实验中,尽管在线圈调谐时并不能使得线圈的谐振频率与原子的进动频率完全一致(即放大倍数不再严格等于Q),这将引起信号和噪声的放大倍数略微不同,但实际调谐时,由于线圈的谐振频率与原子的进动频率相差只在100 Hz量级或更小,相对于其进动频率(104 Hz量级)而言由Q引起的误差可忽略.
在测量信噪比时,误差的主要来源为FID信号的幅值和噪声的测量误差,这是因为每次测量得到的结果都会由于仪器、数据采集方面的因素而存在涨落.对于此部分误差的分析可采用多次测量方法得到各部分误差,再根据(15)式的前两项和误差传递公式计算测得的信噪比的误差,如(16)式所示.
这里值得注意的是,由于噪声测量对测量环境和条件的高度依赖,因此本文在不同的测试条件和环境下对噪声进行了测量.测量结果显示,噪声的测量误差不超过该线圈测量噪声的10%,因此误差按其最大值计算.最后将各部分误差带入(16)式计算SNR的误差,不同的FID线圈的每一项测量误差的值如表2所示.
表2 FID线圈的测量误差
Table 2
| 编号 | Vsig /V | 误差 | VN /V | 误差 | SNR | 误差 |
|---|---|---|---|---|---|---|
| 1 | 0.04312 | 0.00018 | 0.01378 | 0.00069 | 3.130 | 0.16 |
| 2 | 0.22592 | 0.00079 | 0.02121 | 0.00106 | 10.65 | 0.53 |
| 3 | 0.52553 | 0.00156 | 0.03209 | 0.00160 | 16.37 | 0.82 |
| 4 | 1.14638 | 0.00411 | 0.05779 | 0.00289 | 19.84 | 0.99 |
| 5 | 1.61729 | 0.00520 | 0.07510 | 0.00375 | 21.54 | 1.08 |
| 6 | 2.21850 | 0.00630 | 0.12594 | 0.00630 | 17.62 | 0.88 |
| 7 | 4.26661 | 0.00905 | 0.29199 | 0.01460 | 14.61 | 0.73 |
| 8 | 4.62707 | 0.02263 | 0.42443 | 0.02122 | 10.90 | 0.54 |
通过对FID线圈的信号及噪声的测量计算得到不同直径的线圈在d相同的情况下的信噪比的大小,并对信号及噪声分别进行了建模分析.对于信号模型而言,①文中采用的气室是高度直径比接近1的柱形气室,可以使用球形分析模型近似,而针对文献[17]中提到的柱形气室中短气室(short cell)和长气室(long cell)的情况更宜采用(1)~(3)式中的数值方法建立FID信号的分析模型;②文中未将d(气室表面与FID线圈中心的相对距离)作为一个SNR分析模型的关键参数,这是由于d << rcell而忽略了该因素的影响,但实际上SNR的最优值可能会随d的变化存在差异.文中的噪声模型考虑了电阻热噪声和环境磁噪声,尽管FID线圈的电阻值通常在几十Ω量级,但当其直径较小时,电阻热噪声成为了FID线圈噪声的主要来源,此项不可忽略.噪声的大小与测量系统带宽和环境磁噪声水平有关,不同的测试环境具有不同水平的环境磁噪声,该噪声模型对于3He极化系统的FID线圈的噪声分析中是通用的.此外,文中所提出的信噪比分析模型还为磁传感系统中感应线圈的优化设计提供了分析思路.
3 结论
利益冲突
无
参考文献
Fundamentals of spin-exchange optical pumping
[J].
Development of a polarized 3He neutron spin filter based on spin exchange optical pumping at China Mianyang research reactor
[J].
Optically polarized 3He
[J].
An overview of polarized neutron instruments and techniques in Asia pacific
[J].
Hyperpolarised helium-3 (3He) MRI: physical methods for imaging human lung function
[M]// KAUCZOR H, WIELPÜTZ M O. MRI of the lung.
Hyperpolarised gas filling station for medical imaging using polarised 129Xe and 3He
[J].
Relationship between lung and brain injury in covid-19 patients: A hyperpolarized 129Xe-MRI-based 8-month follow-up
[J].
Damaged lung gas exchange function of discharged covid-19 patients detected by hyperpolarized 129Xe MRI
[J].
Absolute magnetometry with 3He
[J].
Ultrasensitive 3He magnetometer for measurements of high magnetic fields
[J].
Searching for new spin- and velocity-dependent interactions by spin relaxation of polarized 3He gas
[J].
Probing the short range spin dependent interactions by polarized 3He atom beams
[J].
Laboratory search for spin-dependent short-range force from axionlike particles using optically polarized 3He gas
[J].
Search for spin-dependent short-range force between nucleons using optically polarized 3He gas
[J].
Polarized 3He as a probe for short-range spin-dependent interactions
[J].
Laser detection of nuclear magnetic resonance FID signal for polarized 3He system
[J].
极化3He系统核磁共振FID信号的激光探测
[J].
DOI:10.11938/cjmr20222987
[本文引用: 1]

极化率测量装置是极化<sup>3</sup>He系统的重要组成部分之一.本文介绍了一套在极化<sup>3</sup>He系统上搭建的激光探测自由感应衰减核磁共振(FID NMR)信号的实验装置,该装置有望为<sup>3</sup>He极化率的高精度实时测量提供新的途径.激光探测法的原理是法拉第旋光效应,该方法使用一束线偏振光探测极化<sup>3</sup>He磁矩绕主磁场进动的FID信号,实验结果表明相较于拾波线圈探测方法,激光探测方法的信噪比提高了106%,对<sup>3</sup>He的极化率测量更精确.该探测方法有望替代传统的拾波线圈,广泛地应用于<sup>3</sup>He极化系统的极化率测量或精密测量实验中.
Pickup coil optimization for polarized 3He system
[J].
Design and implementation of a monitoring system for measuring polarization degree of optical pumping 3He
[J].
光泵抽运3He极化程度监控系统的设计与实现
[J].
DOI:10.11938/cjmr20192720
[本文引用: 2]

极化<sup>3</sup>He的一项重要应用是中子的极化.中国绵阳研究堆(CMRR)已建立国内首个自旋交换光学泵浦(SEOP)极化<sup>3</sup>He中子极化系统.为了监测<sup>3</sup>He的极化率随时间的相对变化情况,本文首先设计了基于核磁共振(NMR)技术的<sup>3</sup>He相对极化率测量系统,通过Matlab控制程序实现了对<sup>3</sup>He相对极化率的定时检测.然后对拾波线圈的构形和信噪比(SNR)进行了优化.结果表明当绕线长度一样时,Brooks构形的线圈有利于提高SNR;当线圈的平均半径为(a<sub>0</sub>+d)/√2(a<sub>0</sub>为<sup>3</sup>He气室的半径,d为拾波线圈与气室之间的距离)时,其SNR最高.最后对该系统的本底噪声进行了测量,发现其主要来源于环境噪声(0.27 μV/√Hz)和数据采集(DAQ)卡的噪声(0.40 μV/√Hz),系统的总噪声功率谱密度约为√0.16+0.073G<sup>2</sup> μV/√Hz(G为放大器的增益倍数).
Exact expression for the magnetic field of a finite cylinder with arbitrary uniform magnetization
[J].