引言
磁共振成像（Magnetic Resonance Imaging，MRI）作为一种无辐射和非侵入影像技术，已成为生物医学研究以及临床诊断的重要工具[1 ⇓ ⇓ -4 ] .其中，高场小动物MRI是一个重要分支，它具有更高的磁场强度和梯度强度，能够实现更高的空间和时间分辨率，使MRI达到分子影像水平.常规1 H MRI主要提供生物体组织结构像信息[5 ] ，13 C、23 Na等杂核MRI能够提供更丰富的生理和代谢功能信息[6 ⇓ ⇓ ⇓ -10 ] .准确测量胶质瘤、认知障碍和中风等代谢异常疾病的损伤，可以提高相关病灶的检测及诊断能力，并据此开发新的治疗方法[11 ⇓ ⇓ -14 ] .因此，发展无创活体代谢MRI技术对代谢异常疾病的研究具有十分重要的意义.
13 C同位素较低的天然丰度（仅为1.1%）和较低的旋磁比（约为1 H旋磁比的1/4）等固有物理性质导致13 C的磁共振信号信噪比较低；对于23 Na等快速弛豫的杂核MRI，T 2 弛豫时间很短，信号采集窗口狭窄，难以快速且精确地获得符合诊断需求的磁共振代谢图像[15 ⇓ ⇓ ⇓ -19 ] .因此，对于小口径小动物成像系统，获取高信噪比和高分辨率的13 C等杂核磁共振代谢图像对磁共振系统的硬件设备要求较高，一方面需要高切换率和高线性度梯度线圈系统进行MRI空间编码，用于提高MRI图像分辨率以及定位精度；另一方面需要设计高灵敏度的磁共振射频线圈，用于提高磁共振信号采集的信噪比，实现快速获取13 C等杂核代谢信息的功能.然而，目前商用的杂核小动物成像线圈和梯度系统通常需要定制，导致部件生产和维修周期长，同时用于小动物MRI的整机设备几乎被国外厂商垄断，使得仪器价格昂贵，国内开展相关研究的单位依然很少，这些因素都严重制约了MRI代谢成像这一重要研究方向的发展.在这种情况下，自主研制高场谱仪小动物杂核MRI代谢成像系统及关键部件就显得尤为重要，相关设备的研制对提高研究效率，减少科研成本，降低小动物MRI研究门槛以及推动相关生物医学研究发展都具有重要意义.
针对以上问题，本文根据自主研制的5 T小动物MRI谱仪系统和小动物13 C代谢MRI检测需求，从梯度线圈和射频线圈出发，设计了基于有限差分流函数方法的小口径梯度线圈（外径51 mm，内径37 mm），以及适用于小口径下1 H/13 C双共振射频线圈（外径36 mm，内径30 mm）.本文采用有限元方法（finite element method，FEM）对设计的梯度线圈以及射频线圈进行了数值模拟[20 ] ，并在自主研制的5 T MRI系统平台对线圈性能进行了验证，成功获取到了13 C标记的尿素水溶液样品的13 C MRI图像和小鼠头部的1 H MRI解剖结构像，实验结果显示利用本文研制的梯度线圈和射频线圈在小口径磁体下进行1 H/13 C MRI实验具有可行性.
1 小口径梯度线圈和射频线圈设计
随着电磁场理论与设计方法的发展和完善，梯度线圈和射频线圈的设计变得更加便利.本文根据自主研制MRI系统的5 T纵向小口径超导磁体磁场结构，简要分析了设计需求，采用有限差分流函数方法设计了一种外径51 mm、内径37 mm的小口径梯度线圈.同时，为了满足小口径小鼠代谢MRI的需要，本文设计了内径30 mm、外径36 mm的1 H/13 C双共振线圈.其中1 H线圈作为小鼠定位像采集线圈，其设计采用马鞍线圈结构，用于提供相对均匀的射频场；由于13 C核天然丰度和磁旋比较低，因此13 C线圈的设计采用表面线圈结构，从而最大限度提高13 C信号的检测灵敏度.进一步利用有限元方法对设计的梯度线圈和射频线圈进行数值模拟与仿真.下文将对设计的内容进行详细的阐述.
1.1 小口径梯度线圈设计
梯度线圈的设计方法主要分为两大类：一种是基于离散电流技术的方法，另一种是基于连续电流的方法[21 ] .基于离散电流技术的方法实施起来比较简单，但优化过程比较耗时；基于连续电流的方法的精度相对较高[22 ] .本文采用基于连续电流方法的有限差分流函数方法对小口径梯度线圈进行设计.
1.1.1 有限差分流函数方法
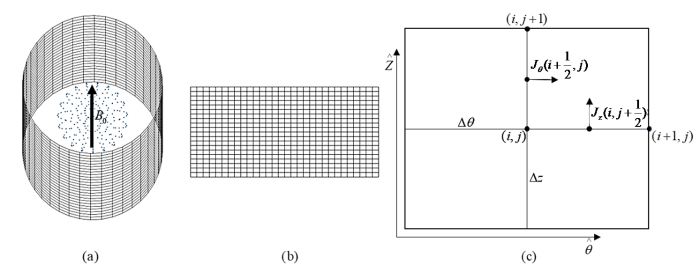
对于纵向超导磁体其磁场方向为腔体轴向方向，在如图1(a) 柱面坐标系下，根据圆筒型梯度线圈的几何特征，线圈圆柱面上的电流密度可以表示为$J(r)={{J}_{z}}{{e}_{z}}+{{J}_{\theta }}{{e}_{\theta }}$ ${{J}_{z}}$ ${{J}_{\theta }}$ z 轴方向电流密度和周向电流密度，图1(a) 中圆柱面内部的目标磁场区域内的点在直角坐标系下的坐标值可以用${{r}_{f}}({{x}_{f}},{{y}_{f}},{{z}_{f}})$ [23 ] ，对于任何一个目标磁场区域内的点，将主磁场方向定义为z 轴方向，则主磁场方向分量可以表示为：
(1) ${{B}_{z}}({{x}_{f}},{{y}_{f}},{{z}_{f}})=\frac{{{\mu }_{0}}}{4\pi }\int_{0}^{2\pi }{\int_{-\frac{1}{2}}^{\frac{1}{2}}{\frac{-{{J}_{\theta }}Q}{{{[{{S}^{2}}+{{Q}^{2}}+{{({{z}_{f}}-\text{zs})}^{2}}]}^{1.5}}}R\text{d}\theta \text{dzs}}}$
(2) $S=-{{x}_{f}}\sin \theta +{{y}_{f}}\theta$
(3) $Q={{x}_{f}}\cos \theta +{{y}_{f}}\sin \theta –R$
图1
图1
圆筒型线圈圆柱面有限差分网格划分. (a)圆柱面网格划分及目标场点；(b)矩形面网格；(c)单元网格节点
Fig. 1
Finite difference meshing of cylindrical coils on cylindrical surface. (a) Cylindrical surface meshing and target field points; (b) rectangular surface meshing; (c) cell mesh nodes
其中，${{\mu }_{0}}$ Q 和S 为定义的中间表达式，R 为线圈圆柱面的底面半径，θ 为圆柱面上的网格节点在柱坐标下的角度值，zs为网格节点的z 轴高度变量，l 为线圈圆柱面高度.圆柱面上的网格节点顺序可以按展开为矩形面上的网格如图1(b) 和图1(c) 所示，从而使用圆柱面上的有限差分网格建立电流密度与电流密度流函数之间的关系[24 ] .图1 为梯度线圈圆柱面有限差分网格划分示意图.
根据流函数的定义[25 ] ，可得网格节点电流密度流函数Ψ和网格节点电流密度J 的有限差分关系：
(4) ${{J}_{z}}(i,j+\frac{1}{2})=\frac{\partial \Psi (i,j+\frac{1}{2})}{\partial \text{zs}}=\frac{\Psi (i,j+1)-\Psi (i,j)}{\Delta \text{zs}}$
(5) ${{J}_{\theta }}(i+\frac{1}{2},j)=\frac{\partial \Psi (i+\frac{1}{2},j)}{R(i+\frac{1}{2},j)\partial \theta }=\frac{\Psi (i,j)-\Psi (i+1,j)}{R(i,j+\frac{1}{2}\Delta \theta )}$
由于目标区域每个目标点的磁场强度都是线圈圆柱平面上所有网格节点上的电流密度流函数在该目标点产生磁场的矢量和，综上可以得到(6)式：
(6) $\left[ \begin{matrix} {{A}_{11}} & {{A}_{12}} & \cdots & {{A}_{1M}} \\ {{A}_{21}} & {{A}_{22}} & \cdots & {{A}_{2M}} \\ \vdots & \vdots & \ddots & \vdots \\ {{A}_{N1}} & {{A}_{N2}} & \cdots & {{A}_{NM}} \\ \end{matrix} \right]\left[ \begin{matrix} {{\Psi }_{1}} \\ {{\Psi }_{2}} \\ \vdots \\ {{\Psi }_{M}} \\\end{matrix} \right]=\left[ \begin{matrix} {{B}_{{{Z}_{1}}}} \\ {{B}_{{{Z}_{2}}}} \\ \vdots \\ {{B}_{{{Z}_{N}}}} \\\end{matrix} \right]$
其中Ψ 1 ~ΨM 为第一个网格节点到第M 个网格节点电流密度函数，$A_{11} \sim A_{N M}$ M 为线圈圆柱面网格划分得到的所有网格节点的总数目，N 为目标点的总数目，$B_{Z_{1}} \sim B_{Z_{N}}$ z 轴方向分量到第N 个目标点磁场强度z 轴方向分量.
通过构造约束矩阵和采用Tikhonov正则化方法即可求解方程组，由于(6)式为病态方程组，采用Tikhonov正则化方法可求得近似解[26 ] ，Tikhonov正则化方法的一般形式为：
(7) $\min \{||Ax-b||_{2}^{2}+{{\lambda }^{2}}||Lx||_{2}^{2}\}$
(7)式中λ 为正则化参数，L λ 的作用是平衡数据拟合项$||Ax-b|{{|}_{2}}$ $||Lx|{{|}_{2}}$ L λ 是Tikhonov正则化能否成功的关键.(7)式对x 求偏导化简可得：
(8) $({{A}^{T}}A+{{\lambda }^{2}}{{L}^{T}}L)x={{A}^{T}}b$
当$({{A}^{T}}A+{{\lambda }^{2}}{{L}^{T}}L)$
(9) ${{x}_{\lambda }}={{({{A}^{T}}A+{{\lambda }^{2}}{{L}^{T}}L)}^{-1}}{{A}^{T}}b$
由于梯度线圈电感越小切换率越高，将线圈的电感${{L}_{1}}$
(10) ${{L}_{1}}=\frac{{{\mu }_{0}}}{4\pi {{I}^{2}}}\int_{V}{\frac{J(r)\cdot J({r}')}{\left| r-{r}' \right|}\text{d}V}$
将电感约束函数(10)式转化为关于网格节点电流密度流函数Ψ 的表达式，如(11)式：
(11) ${{L}_{1}}={{(L\Psi )}^{T}}(L\Psi )$
从而得到可以用于圆筒型梯度线圈的约束矩阵L
(12) ${{I}_{0}}=\frac{{{\Psi }_{\max }}-{{\Psi }_{\min }}}{{{n}_{\text{coil}}}}$
其中${{\Psi }_{\max }}$ ${{\Psi }_{\min }}$ ${{n}_{\text{coil}}}$ $I_{0}$
1.1.2 梯度线圈设计与仿真
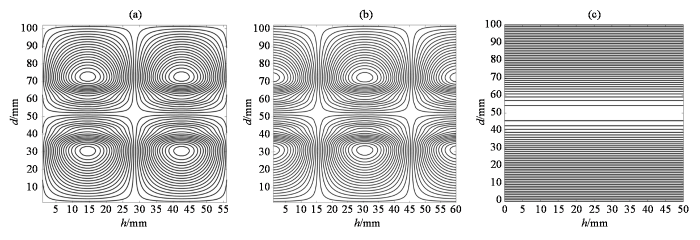
根据实际纵向超导磁体的磁场强度和结构，设计x 、y 、z 方向梯度线圈的半径为分别为24.5 mm、25.5 mm和23 mm，目标场为直径40 mm的球体，在1 A激励电流下目标区域产生的最大磁场强度为0.2 mT，同时为了保证高切换率以电感最小作为约束条件，将上述值作为设计参数代入求解(6)式，得到如图2 所示三个方向的平面绕线模式（d 为展开后的长度，h 为线圈高度）.
图2
图2
圆筒型梯度线圈绕线模式. (a) x 线圈；(b) y 线圈；(c) z 线圈
Fig. 2
The winding pattern of cylindrical gradient coil. (a) x coil; (b) y coil; (c) z coil
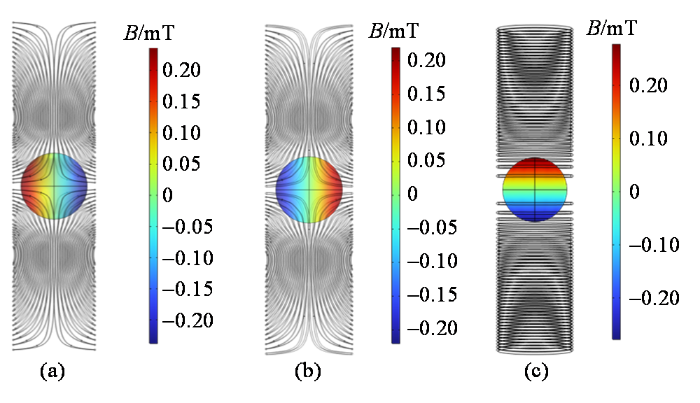
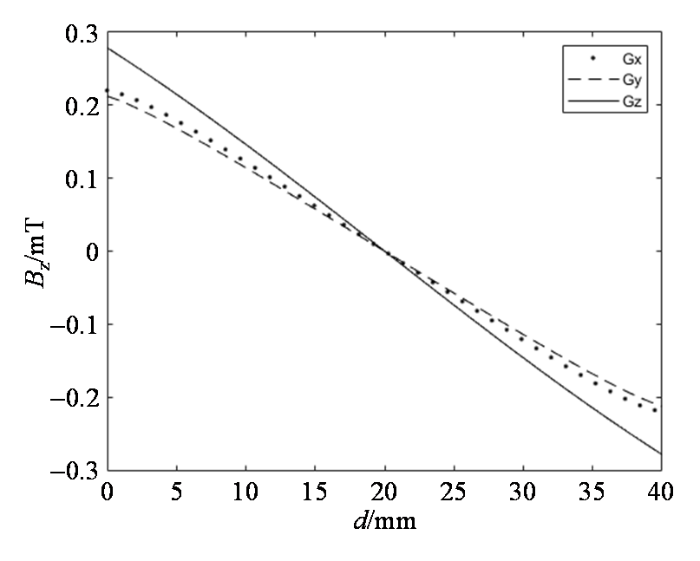
梯度线圈设计属于低频电磁场问题，在实物制作前对求解的绕线模式进行静磁场仿真很大程度上可以反映梯度线圈性能，参考仿真结果反过来可以优化绕线模式，图3 是使用有限元方法对梯度线圈绕线模式产生的磁场分布进行数值模拟仿真的结果，其中激励电流为1 A，中心球体为目标区域的磁场分布，目标区域球体沿中心线40 mm磁场大小数值分布仿真结果如图4 所示，仿真结果显示设计的x 、y 、z 三个方向梯度线圈在目标磁场区域有均匀的线性梯度磁场分布.
图3
图3
梯度线圈磁场分布. (a) x 梯度线圈磁场分布；(b) y 梯度线圈磁场分布；(c) z 梯度线圈磁场分布
Fig. 3
The magnetic field distribution of gradient coil. (a) x gradient coil; (b) y gradient coil; (c) z gradient coil
图4
图4
目标区域沿中心直线分布梯度磁场大小数值分布仿真结果
Fig. 4
Numerical distribution simulation results of magnitude of the gradient magnetic field distributed linearly along the center of the target area
1.2 小口径1 H/13 C双共振射频线圈设计
常见的射频线圈有鸟笼线圈、马鞍线圈、表面线圈和阵列线圈，其中鸟笼线圈的射频场均匀性较好，马鞍线圈次之，但二者的灵敏度相对较低，表面线圈在牺牲射频场均匀性的前提下具有较高的检测灵敏度，阵列线圈兼顾较好的射频场均匀性和较高的检测灵敏度，具有良好的射频性能，但阵列线圈实现起来相对较为复杂[27 ] .本文选择马鞍线圈和表面线圈作为射频线圈的设计方案.
1.2.1 1 H/13 C双共振线圈方案分析
在小口径磁体腔中除去梯度线圈占用的空间后，留给射频线圈的空间仅有37 mm，再减去放置小鼠的空间30 mm和线圈支撑结构石英玻璃管1 mm的厚度后，用0.2 mm的薄铜皮作为屏蔽结构，留给线圈的厚度仅剩约2 mm.由于鸟笼线圈需在腿或端环焊接电容，2 mm的空间使其不适合作为小口径下射频线圈的设计方案，同时阵列线圈在小口径下实现起来难度较高.考虑到1 H线圈作为定位功能需要一定的射频场均匀性，而13 C线圈由于13 C核的低信噪比对检测线圈的灵敏度提出了更高要求，因此本文选择马鞍线圈作为1 H射频线圈方案，选择表面线圈作为13 C射频线圈方案.
1.2.2 1 H/13 C双共振线圈设计与仿真
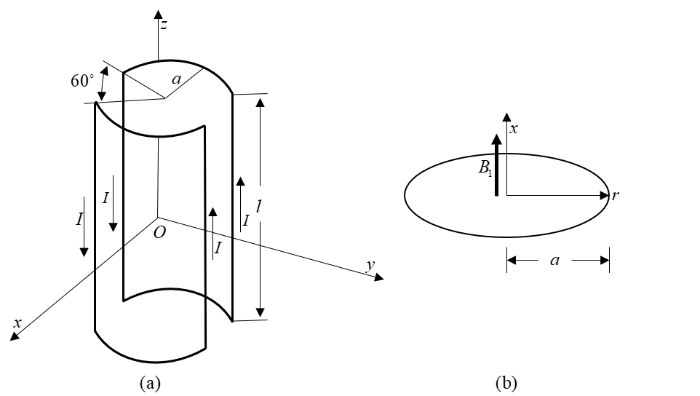
马鞍线圈作为结构简单且射频场相对均匀的线圈设计方案[28 ] ，如图5(a) 所示，假设其圆弧半径为a ，线圈长度为l ，则当线圈长度与圆弧半径的比值l /a =3.322，线圈开角为60˚时，可在线圈中心获得均匀度最好的磁场[29 ] .
图5
图5
射频线圈结构示意图. (a)马鞍线圈；(b)表面线圈
Fig. 5
The structure diagram of RF coil. (a) Saddle coil; (b) surface coil
如图5(b) 所示，表面线圈作为最简单的线圈结构，其磁场分布根据毕奥萨伐尔定律，圆形表面线圈产生的磁场可以表示为[30 ] ：
(13) ${{B}_{1}}=\frac{I{{\mu }_{0}}{{a}^{2}}}{2{{({{a}^{2}}+{{x}^{2}})}^{3/2}}}$
其中$I$ $a$ $\mu_{0}$
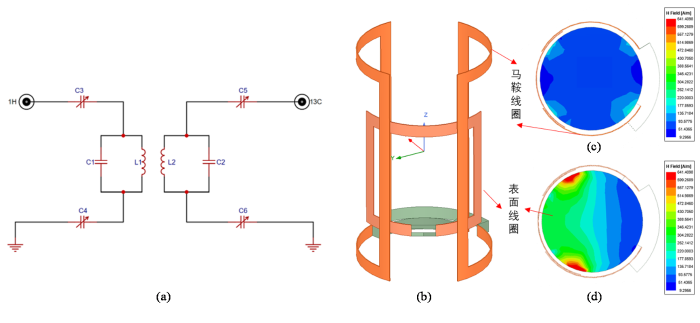
由于线圈是贴在圆柱表面，1 H马鞍线圈的圆弧半径为16 mm，线圈长度为53 mm，开角为60˚，实际13 C线圈为保证足够的成像视野设计成矩形圆弧，圆弧对应弧度为120˚，长度为30 mm.1 H/13 C线圈电路结构如图6(a) 所示，其中${{L}_{1}}$ ${{L}_{2}}$ ${{C}_{1}}$ ${{C}_{2}}$ ${{C}_{3}}$ ${{C}_{4}}$ ${{C}_{5}}$ ${{C}_{6}}$ 图6(b) 所示，利用有限元方法进行数值模拟仿真观察磁场分布，设置线圈材料为铜（copper），其电导率和相对磁导率分别为5.8×107 S/m和0.999 9912.如图6(c) 和6(d) 所示，从仿真结果可以看出，当马鞍线圈和表面线圈分别工作在1 H/13 C对应频率212.6 MHz和53.47 MHz时，马鞍线圈具有相对均匀的射频场分布，表面线圈在局部空间中具有较好的灵敏度，仿真结果与1.2.1节设计分析一致.
图6
图6
1 H/13 C双共振线圈电路原理图与仿真结果. (a)线圈电路原理图；(b)线圈磁场仿真模型；(c) 1 H马鞍线圈磁场分布；(d) 13 C表面线圈磁场分布
Fig. 6
1 H/13 C dual resonance coil circuit schematic and simulation results. (a) Coil circuit schematic; (b) simulation model of coil magnetic field; (c) magnetic field distribution of 1 H saddle coil; (d) magnetic field distribution of 13 C surface coil
2 线圈实物制作与电性能测试
2.1 梯度线圈实物制作与电性能测试
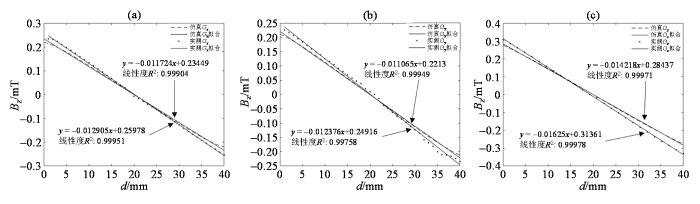
梯度线圈实际制作时采用1.5 mm空心铜管绕线用于水冷散热，对制作完成的梯度线圈利用高精度数字高斯计（翠海磁电公司，型号CH-1600）对梯度线圈的磁场分布进行测量，使用高精度直流稳压电源（国睿安泰信公司，型号APS3005S-3D）输出1 A电流，分别测试x 、y 、z 梯度线圈在1 A电流下产生的z 分量的磁场大小与分布，如图7 所示，其实测磁场分布与仿真结果吻合，为实现MRI的精准空间定位提供了保障.
图7
图7
梯度线圈磁场分布仿真与实测线性拟合结果. (a) x 梯度线圈仿真与实测线性拟合结果；(b) y 梯度线圈仿真与实测线性拟合结果；(c) z 梯度线圈仿真与实测线性拟合结果
Fig. 7
Linear fitting results of gradient coil magnetic field distribution. (a) The simulated and measured linear fitting results of x gradient coil; (b) the simulated and measured linear fitting results of y gradient coil; (c) the simulated and measured linear fitting results of z gradient coil
对实测的磁场分布结果进行线性拟合后处理可以得到梯度线圈的效率和线性度，利用数字万用表测量制作的梯度线圈的电感和电阻.对于梯度线圈的切换率SR,可由下式求得[22 ] ：
(14) $SR=\frac{\eta (V-RI)}{L}$
其中$\eta$ R 和L 为梯度线圈的电阻和电感，V 和I 为MRI系统配置的梯度功率放大器的最大电压和电流，本系统使用的梯度功率放大器最大电流和电压分别为200 A和300 V，由此计算出理论上x 、y 、z 梯度线圈的SR分别是25 037.85 T/m/s，22 717.88 T/m/s，18 050.88 T/m/s.由于实际梯度线圈工作时考虑涡流等影响，梯度脉冲设置有上升沿和下降沿时间，由此实际使用切换率可由(15)式计算得到：
(15) $SR={{G}_{\max }}/{{T}_{\text{rise}}}$
T rise 为上升下降沿时间，本文系统设置的T rise 为82 μs，实际成像实验先用1 H核对梯度线圈最大梯度G max 进行标定，使成像尺寸与实际相符，成像实验将在第3节详细描述.通过以上测试方法测得梯度线圈相关性能参数如表1 所示，从表中可以看出实际的梯度线圈具有良好的线性度，x 、y 、z 三个方向分别为0.999 51、0.997 58、0.999 78，满足成像需求的梯度线性度要求大于等于95%，因此本文设计的梯度线圈满足实际成像需求.同时由于线圈口径较小，G max 也超过了0.8 T/m，根据该梯度强度计算出x 、y 、z 三个方向实际使用的切换率分别为10 000 T/m/s、9 756.1 T/m/s、12 195.1 T/m/s。最大梯度强度数值是商用人体MRI系统平台（G max <0.1 T/m）的10倍左右，同时目前文献中报道的商用小动物MRI和人体头部MRI系统的最大SR分别为4 200 T/m/s（口径300 mm）和600 T/m/s（口径390 mm）[31 ,32 ] ，相对于小动物和人体MRI系统，本文设计的小口径梯度线圈系统（口径37 mm）能够实现更高SR的13 C磁共振代谢成像研究.
2.2 射频线圈实物制作与电性能测试
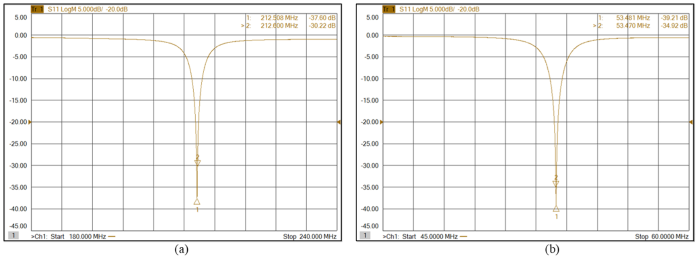
射频线圈定值电容采用Dalicap公司DLC系列无磁电容，可调电容采用Voltronics公司的无磁可调电容.5 T磁场下1 H/13 C线圈工作频率分别为212.6 MHz和53.47 MHz.利用ROHDE&SCHWARZ公司的ZNB20矢量网络分析仪对线圈进行测试，图8 为1 H/13 C双共振线圈输入反射系数S11测试结果，结果显示1 H/13 C双共振线圈能在各自谐振点良好的工作，1 H线圈反射系数优于-30 dB，13 C线圈反射系数优于-34 dB.
图8
图8
1 H/13 C线圈的S参数. (a) 1 H线圈S11参数；(b) 13 C线圈S11参数
Fig. 8
S-parameters of 1 H/13 C coils. (a) S11 parameters of 1 H coil; (b) S11 parameters of 13 C coil
3 小口径1 H/13 C双共振射频线圈与梯度线圈成像测试
将本文设计与制作的小口径双共振射频线圈与梯度线圈进行集成后，安装在本课题组自主研制的5 T MRI平台中，对设计的梯度线圈和射频线圈进行MRI测试，如图9 所示.测试样品为6 mol/L 13 C标记的尿素水溶液（13 C-Urea水溶液），样品量约为2 mL，装入外径16 mm、内径14 mm的玻璃瓶内，液面高度约为20 mm，采用SE序列对1 H/13 C水模样品进行信号采集，1 H成像参数为：扫描次数（NS）=1，重复时间（TR）= 500 ms，回波时间（TE）= 8 ms，成像视野（FOV）= 50 mm×50 mm，层厚（slice thickness）= 2 mm，矩阵大小（matrix size）= 128×128；13 C成像参数为：NS = 1，TR = 2 000 ms，TE = 22 ms，FOV = 25 mm×25 mm，slice thickness = 5 mm，matrix size = 128×128.样品实物及成像结果如图10 所示，1 H和13 C磁共振图像大小差异来源于两种核素的磁旋比差异，后期可以通过图像线性插值或梯度缩放实现1 H和13 C的图像融合，测试结果显示1 H和13 C图像轮廓清晰，所研制的梯度线圈与射频线圈均具有良好的MRI性能，能够满足小口径下磁共振代谢成像的需求.
图9
图9
自主研制5 T磁共振成像系统平台实物图. (a) 5 T纵向超导磁体及自主研制高场多核MRI谱仪系统，(b)自主研制小口径梯度线圈，(c)自主研制小口径1 H/13 C双共振射频线圈
Fig. 9
Picture of the home-made 5 T magnetic resonance imaging system. (a) 5 T longitudinal superconducting magnet and home-made high-field multinuclear MRI spectrometer system; (b) home-made small bore gradient coils; (c) home-made small bore 1 H/13 C dual-resonance RF coils
图10
图10
1 H/13 C双共振线圈MRI测试样品及成像结果. (a) 6 mol/L 13 C-Urea水溶液样品；(b) 1 H横断位磁共振图像；(c) 13 C横断位磁共振图像
Fig. 10
MRI test samples and imaging results for 1 H/13 C dual resonance coil. (a) 6 mol/L 13 C-Urea aqueous solution samples; (b) 1 H transverse MRI images; (c) 13 C transverse MRI images
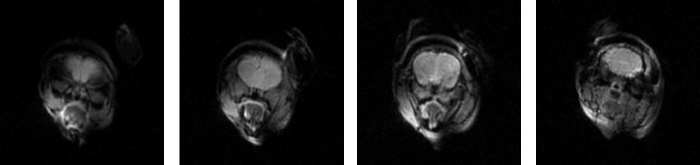
同时，为了测试本文提出的梯度线圈和射频线圈设计方案用于小口径高场小动物MRI的可行性，我们还开展了针对活体小鼠头部的1 H MRI实验，成像参数为：NS = 1，TR = 2 500 ms，TE = 8 ms，FOV = 35 mm ×35 mm，slice thickness = 2 mm，matrix size = 160×160，扫描层数（slice）= 4，实验结果如图11 所示，图中依次为小鼠头部连续多层切片MRI图像，可以清晰的分辨出小鼠头部解剖结构，为后续开展1 H/13 C融合的活体磁共振代谢成像提供实验平台.
图11
图11
活体小鼠头部多层切片1 H磁共振图像
Fig. 11
1 H magnetic resonance images of multilayer slices in living mice head
4 结论
本文对梯度线圈和射频线圈的设计方法进行了简要阐述，设计了一套小口径MRI梯度线圈与1 H/13 C双共振射频线圈，利用有限元方法分别对梯度线圈和1 H/13 C射频线圈进行了数值模拟仿真分析，仿真结果表明梯度线圈具有良好的效率和线性度，1 H马鞍线圈具有相对良好的射频场均匀性，13 C表面线圈的磁场分布满足实际13 C成像的要求.利用高斯计对实际梯度线圈的磁场分布进行了测试，验证了所设计的梯度线圈具有相对良好的线性度和效率；利用矢量网络分析仪对1 H/13 C射频线圈的电性能进行了测试，结果表明1 H/13 C射频线圈能够良好的工作于其对应的频率.针对13 C标记的Urea水溶液和活体小鼠，在自主研制的5 T MRI系统平台对所设计的小口径梯度线圈与射频线圈进行了成像性能验证，实验结果表明所设计的梯度线圈与射频线圈的性能可满足小口径下MRI的需求，验证了设计方案的可行性，为将来进一步开展基于动态核极化的13 C磁共振代谢成像奠定了基础.
利益冲突
参考文献
View Option
[1]
CHEN H Y ZHAO S L LI X N , et al . B 1 mapping on low-field permanent magnet MRI scanner
[J]. Chinese J Magn Reson , 2018 , 35 (4 ): 498 -504 .
[本文引用: 1]
陈海燕 , 赵世龙 , 李晓南 , 等 . 低场永磁体磁共振射频场映像
[J]. 波谱学杂志 , 2018 , 35 (4 ): 498 -504 .
DOI:10.11938/cjmr20182661
[本文引用: 1]
射频场映像是通过一定算法对磁共振射频线圈的发射场进行重建的方法.高场下的射频场经过生物组织时会发生明显变化，在其基础上可以反演生物组织体内电特性，进而对癌症等疾病进行早期诊断，是对生物组织的磁共振结构成像的有力补充.目前为止，射频场映像和电特性研究都以高场鸟笼线圈为主，对低场下的相控阵研究较少.本文主要研究了低场永磁体磁共振射频场的均匀度.有限元仿真和实验验证了在17.8 MHz激励下，射频场在空载和负载下均匀度均发生较大变化.射频场均匀度在负载下的改变在一定程度上可以反映负载生物组织的电特性，对磁共振电特性实用化研究提供了一定的参考价值.
[2]
LUO J LIU S P YANG X , et al . Design of a 5 T non-magnetic magnetic resonance radio frequency power amplifier
[J]. Chinese J Magn Reson , 2022 , 39 (2 ): 163 -173 .
[本文引用: 1]
骆俊 , 刘盛平 , 杨兴 , 等 . 一种无磁化的5 T磁共振射频功率放大器设计
[J]. 波谱学杂志 , 2022 , 39 (2 ): 163 -173 .
DOI:10.11938/cjmr20212958
[本文引用: 1]
本文介绍了一种可以不接环形器，并在扫描间使用的5 T磁共振射频功率放大器（RFPA）.该RFPA基于驻波高耐受的横向扩散金属氧化物半导体（LDMOS）功率管进行设计，共包含三级放大电路.针对传统磁共振RFPA中带磁芯的传输线变压器进行了无磁化的设计，加强了对反射功率的监控，采用模拟负反馈技术实现了对RFPA非线性的自动矫正.测试结果显示该RFPA的输出功率为2 kW，在负载扰动（反射系数Г < 0.5）时，40 dB动态输入范围，其增益线性度≤ 1 dB，相位线性度≤ 10˚，满足成像需求，验证了该设计方案的合理性与可行性.
[3]
LIAO Z W CHEN J F YANG C S , et al . A Design scheme for 1 H/31 P dual-nuclear parallel MRI coil
[J]. Chinese J Magn Reson , 2020 , 37 (3 ): 273 -282 .
[本文引用: 1]
廖志文 , 陈俊飞 , 杨春升 , 等 . 1 H/31 P双核并行磁共振成像线圈的研究与设计
[J]. 波谱学杂志 , 2020 , 37 (3 ): 273 -282 .
DOI:10.11938/cjmr20192737
[本文引用: 1]
本文通过对鸟笼线圈原理和阵列线圈去耦原理的分析，提出了一种适用于自主研发的多核并行磁共振成像（MRI）系统的双核并行成像线圈设计方案，并在电感去耦的基础上提出LC并联trap去耦法，提高了去耦方法的可适性．依据设计方案制作了<sup>1</sup>H/<sup>31</sup>P双核并行成像线圈，并将其应用于4.7 T磁体系统，利用自主研发的多核并行MRI系统进行了并行成像实验测试，成功获得了<sup>1</sup>H和<sup>31</sup>P的并行磁共振图像，验证了设计方案的可行性．
[4]
HOU S L XIE H T HOU X W , et al . Gradient coils in permanent magnet miniature magnetic resonance imagers and image quality
[J]. Chinese J Magn Reson , 2012 , 29 (4 ): 508 -520 .
[本文引用: 1]
侯淑莲 , 谢寰彤 , 侯晓吻 , 等 . 永磁微型磁共振成像仪的梯度线圈与图像质量
[J]. 波谱学杂志 , 2012 , 29 (4 ): 508 -520 .
[本文引用: 1]
通过理论分析结合计算机仿真试验剖析了磁共振成像(MRI)中梯度场线性对图像质量影响的原理，在梯度场线性有缺陷的情况下，用实例和计算机模拟直观的展示了重建图像和模拟结果. 结合研发实践发现，在永磁微小口径、低场强用于鼠类等小动物成像情况下，对梯度场线性度的要求远高于文献中提出的指标. 依靠软件改进，图像没有本质的提高，尝试补偿技术耗时费力效果也不理想. 说明了对永磁微小口径成像仪研发线性度更好的梯度线圈是提高图像质量的关键技术之一. 揭示了在理想条件下普适的理论原理，在不同的实践条件下有不同的趋近理想条件要求. 将具有独立知识产权的高线性梯度线圈安装在自行研制的仪器上得到了较好的图像.
[5]
FENZL M BACKENS M BODEA S , et al . Impact of cannabis use on brain metabolism using 31 P and 1 H magnetic resonance spectroscopy
[J]. Neuroradiology , 2023 , 65 (11 ): 1631 -1648 .
[本文引用: 1]
[6]
DEEN S S ROONEY C SHINOZAKI A , et al . Hyperpolarized carbon 13 MRI: clinical applications and future directions in oncology
[J]. Radiol Imaging Cancer , 2023 , 5 (5 ): e230005.
[本文引用: 1]
[7]
WANG G X YANG H Y LI J , et al . Overview and progress of X-nuclei magnetic resonance imaging in biomedical studies
[J]. Magn Reson Lett , 2023 , 3 (4 ): 327 -343 .
[本文引用: 1]
[8]
BHATIA A LEE V K QIAN Y , et al . Quantitative sodium (23 Na) MRI in pediatric gliomas: initial experience
[J]. Diagnostics (Basel) , 2022 , 12 (5 ): 12 -23 .
[本文引用: 1]
[9]
GORALSKI J L CHUNG S H CEPPE A S , et al . Dynamic perfluorinated gas MRI shows improved lung ventilation in people with cystic fibrosis after elexacaftor/tezacaftor/ivacaftor: an observational study
[J]. J Clin Med , 2022 , 11 (20 ): 6160.
[本文引用: 1]
[10]
BARANYAI Z CARNIATO F NUCERA A , et al . Defining the conditions for the development of the emerging class of Fe(III)-based MRI contrast agents
[J]. Chem Sci , 2021 , 12 (33 ): 11138 -11145 .
[本文引用: 1]
[11]
JIANG W Q JIANG M A R , et al . The principle of pH imaging with MR and its research progress on the formation mechanism and development of tumor acidic microenvironment
[J]. Chin J Magn Reson Imaging , 2021 , 12 (2 ): 121 -124 .
[本文引用: 1]
姜炜琪 , 姜萌 , 阿荣 , 等 . 磁共振pH成像原理及其在肿瘤酸性微环境形成机制及其发展演变中的研究进展
[J]. 磁共振成像 , 2021 , 12 (2 ): 121 -124 .
[本文引用: 1]
[12]
LIM H THIND K MARTINEZ-SANTIESTEBAN F M , et al . Construction and evaluation of a switch-tuned 13 C-1 H birdcage radiofrequency coil for imaging the metabolism of hyperpolarized 13 C-enriched compounds
[J]. J Magn Reson Imaging , 2014 , 40 (5 ): 1082 -1090 .
[本文引用: 1]
[13]
BERNARDTIFFON , JOELMISPELTER , LHOSTE J-M , et al . A carbon-13 in viva double surface-coil NMR probe with efficient
[J]. J Magn Reson , 1986 , 68 : 544 -550 .
[本文引用: 1]
[14]
QIAO J G WU H ZHANG W G , et al . Progress in hyperpolarization 13 C magnetic resonance imaging of glioma
[J]. Int J of Med Radiol , 2022 , 45 (3 ): 293 -297 .
[本文引用: 1]
谯金果 , 吴昊 , 张伟国 , 等 . 脑胶质瘤超极化13 C-MRI研究进展
[J]. 国际医学放射学杂志 , 2022 , 45 (3 ): 293 -297 .
[本文引用: 1]
[15]
CAO P ZHANG X PARK I , et al . 1 H-13 C independently tuned radiofrequency surface coil applied for in vivo hyperpolarized MRI
[J]. Magn Reson Med , 2016 , 76 (5 ): 1612 -1620 .
[本文引用: 1]
[16]
HANSEN R B SÁNCHEZ-HEREDIA J D BØGH N , et al . Coil profile estimation strategies for parallel imaging with hyperpolarized 13 C MRI
[J]. Magn Reson Med , 2019 , 82 (6 ): 2104 -2117 .
[本文引用: 1]
[17]
SANCHEZ-HEREDIA J D OLIN R B GRIST J T , et al . RF coil design for accurate parallel imaging on 13 C MRSI using 23 Na sensitivity profiles
[J]. Magn Reson Med , 2022 , 88 (3 ): 1391 -1405 .
[本文引用: 1]
[18]
WANG W SANCHEZ-HEREDIA J D OLIN R B , et al . A cryogenic 14-channel 13 C receiver array for 3 T human head imaging
[J]. Magn Reson Med , 2023 , 89 (3 ): 1265 -1277 .
[本文引用: 1]
[19]
LUCHINAT E BARBIERI L CREMONINI M , et al . Protein in-cell NMR spectroscopy at 1.2 GHz
[J]. J Biomol NMR , 2021 , 75 (2-3 ): 97 -107 .
[本文引用: 1]
[20]
ZENG W LIU G R , et al . Smoothed finite element methods (S-FEM): an overview and recent developments
[J]. Arch Computat Methods Eng , 2018 , 25 (2 ): 397 -435 .
[本文引用: 1]
[21]
LITTIN S JIA F AMREIN P , et al . Methods: of stream functions and thin wires: an intuitive approach to gradient coil design
[J]. Front Phys , 2021 , 9 (3 ): 142 -153 .
[本文引用: 1]
[22]
樊萌 . 磁共振系统匀场线圈与梯度线圈设计研究 [D]. 北京 : 中国科学院大学 , 2021 .
[本文引用: 2]
[23]
HIDALGO-TOBON S S . Theory of gradient coil design methods for magnetic resonance imaging
[J]. Concepts Magn Reson A , 2010 , 36A (4 ): 223 -242 .
[本文引用: 1]
[24]
WANG Y H WANG W M LIU H , et al . Gradient coil design with enhanced shielding constraint for a cryogen-free superconducting MRI system
[J]. Magn Reson Lett , 2024 , 4 (1 ): 100086.
[本文引用: 1]
[25]
PEEREN G N . Stream function approach for determining optimal surface currents
[J]. J Comp Phys , 2003 , 191 (1 ): 305 -321 .
[本文引用: 1]
[26]
BOT R I CSETNEK E R LASZLO S C , et al . Tikhonov regularization of a second order dynamical system with Hessian driven damping
[J]. Math Program , 2021 , 189 (1-2 ): 151 -186 .
DOI:10.1007/s10107-020-01528-8
PMID:34720194
[本文引用: 1]
We investigate the asymptotic properties of the trajectories generated by a second-order dynamical system with Hessian driven damping and a Tikhonov regularization term in connection with the minimization of a smooth convex function in Hilbert spaces. We obtain fast convergence results for the function values along the trajectories. The Tikhonov regularization term enables the derivation of strong convergence results of the trajectory to the minimizer of the objective function of minimum norm.© The Author(s) 2020.
[27]
章萌 . 1 H/31 P/23 Na三核磁共振成像线圈的研究与设计北京 : 中国科学院大学 , 2021 .
[本文引用: 1]
[28]
NESPOR D BARTUSEK K DOKOUPIL Z , et al . Comparing saddle, slotted-tube and parallel-plate coils for magnetic resonance imaging
[J]. Meas Sci Rev , 2014 , 14 (3 ): 171 -176 .
[本文引用: 1]
[29]
GINSBERG D M MELCHNER M J . Optimum geometry of saddle shaped coils for generating a uniform magnetic field
[J]. Rev Sci Instrum , 1970 , 41 (1 ): 122 -123 .
[本文引用: 1]
[30]
ANGELIDIS P VASSILIADIS K SERGIADIS G D , et al . Lowest mutual coupling between closely spaced loop antennas
[J]. IEEE T Antenn Propag , 1991 , 39 (7 ): 949 -953 .
[本文引用: 1]
[31]
WU D KANG L Y LI H T , et al . Developing an AI-empowered head-only ultra-high-performance gradient MRI system for high spatiotemporal neuroimaging
[J]. NeuroImage , 2024 , 290 (3 ): 120553.
[本文引用: 1]
[32]
BRUKER . Bio_Spec 94_30_CN[OL] . [2019 ]. https://www.bruker.com/en/products-and-solutions/preclinical-imaging/mri/biospec/biospec-70-30-and-94-30.html.
URL
[本文引用: 1]
B 1 mapping on low-field permanent magnet MRI scanner
1
2018
... 磁共振成像（Magnetic Resonance Imaging，MRI）作为一种无辐射和非侵入影像技术，已成为生物医学研究以及临床诊断的重要工具[1 ⇓ ⇓ -4 ] .其中，高场小动物MRI是一个重要分支，它具有更高的磁场强度和梯度强度，能够实现更高的空间和时间分辨率，使MRI达到分子影像水平.常规1 H MRI主要提供生物体组织结构像信息[5 ] ，13 C、23 Na等杂核MRI能够提供更丰富的生理和代谢功能信息[6 ⇓ ⇓ ⇓ -10 ] .准确测量胶质瘤、认知障碍和中风等代谢异常疾病的损伤，可以提高相关病灶的检测及诊断能力，并据此开发新的治疗方法[11 ⇓ ⇓ -14 ] .因此，发展无创活体代谢MRI技术对代谢异常疾病的研究具有十分重要的意义. ...
低场永磁体磁共振射频场映像
1
2018
... 磁共振成像（Magnetic Resonance Imaging，MRI）作为一种无辐射和非侵入影像技术，已成为生物医学研究以及临床诊断的重要工具[1 ⇓ ⇓ -4 ] .其中，高场小动物MRI是一个重要分支，它具有更高的磁场强度和梯度强度，能够实现更高的空间和时间分辨率，使MRI达到分子影像水平.常规1 H MRI主要提供生物体组织结构像信息[5 ] ，13 C、23 Na等杂核MRI能够提供更丰富的生理和代谢功能信息[6 ⇓ ⇓ ⇓ -10 ] .准确测量胶质瘤、认知障碍和中风等代谢异常疾病的损伤，可以提高相关病灶的检测及诊断能力，并据此开发新的治疗方法[11 ⇓ ⇓ -14 ] .因此，发展无创活体代谢MRI技术对代谢异常疾病的研究具有十分重要的意义. ...
Design of a 5 T non-magnetic magnetic resonance radio frequency power amplifier
1
2022
... 磁共振成像（Magnetic Resonance Imaging，MRI）作为一种无辐射和非侵入影像技术，已成为生物医学研究以及临床诊断的重要工具[1 ⇓ ⇓ -4 ] .其中，高场小动物MRI是一个重要分支，它具有更高的磁场强度和梯度强度，能够实现更高的空间和时间分辨率，使MRI达到分子影像水平.常规1 H MRI主要提供生物体组织结构像信息[5 ] ，13 C、23 Na等杂核MRI能够提供更丰富的生理和代谢功能信息[6 ⇓ ⇓ ⇓ -10 ] .准确测量胶质瘤、认知障碍和中风等代谢异常疾病的损伤，可以提高相关病灶的检测及诊断能力，并据此开发新的治疗方法[11 ⇓ ⇓ -14 ] .因此，发展无创活体代谢MRI技术对代谢异常疾病的研究具有十分重要的意义. ...
一种无磁化的5 T磁共振射频功率放大器设计
1
2022
... 磁共振成像（Magnetic Resonance Imaging，MRI）作为一种无辐射和非侵入影像技术，已成为生物医学研究以及临床诊断的重要工具[1 ⇓ ⇓ -4 ] .其中，高场小动物MRI是一个重要分支，它具有更高的磁场强度和梯度强度，能够实现更高的空间和时间分辨率，使MRI达到分子影像水平.常规1 H MRI主要提供生物体组织结构像信息[5 ] ，13 C、23 Na等杂核MRI能够提供更丰富的生理和代谢功能信息[6 ⇓ ⇓ ⇓ -10 ] .准确测量胶质瘤、认知障碍和中风等代谢异常疾病的损伤，可以提高相关病灶的检测及诊断能力，并据此开发新的治疗方法[11 ⇓ ⇓ -14 ] .因此，发展无创活体代谢MRI技术对代谢异常疾病的研究具有十分重要的意义. ...
A Design scheme for 1 H/31 P dual-nuclear parallel MRI coil
1
2020
... 磁共振成像（Magnetic Resonance Imaging，MRI）作为一种无辐射和非侵入影像技术，已成为生物医学研究以及临床诊断的重要工具[1 ⇓ ⇓ -4 ] .其中，高场小动物MRI是一个重要分支，它具有更高的磁场强度和梯度强度，能够实现更高的空间和时间分辨率，使MRI达到分子影像水平.常规1 H MRI主要提供生物体组织结构像信息[5 ] ，13 C、23 Na等杂核MRI能够提供更丰富的生理和代谢功能信息[6 ⇓ ⇓ ⇓ -10 ] .准确测量胶质瘤、认知障碍和中风等代谢异常疾病的损伤，可以提高相关病灶的检测及诊断能力，并据此开发新的治疗方法[11 ⇓ ⇓ -14 ] .因此，发展无创活体代谢MRI技术对代谢异常疾病的研究具有十分重要的意义. ...
1 H/31 P双核并行磁共振成像线圈的研究与设计
1
2020
... 磁共振成像（Magnetic Resonance Imaging，MRI）作为一种无辐射和非侵入影像技术，已成为生物医学研究以及临床诊断的重要工具[1 ⇓ ⇓ -4 ] .其中，高场小动物MRI是一个重要分支，它具有更高的磁场强度和梯度强度，能够实现更高的空间和时间分辨率，使MRI达到分子影像水平.常规1 H MRI主要提供生物体组织结构像信息[5 ] ，13 C、23 Na等杂核MRI能够提供更丰富的生理和代谢功能信息[6 ⇓ ⇓ ⇓ -10 ] .准确测量胶质瘤、认知障碍和中风等代谢异常疾病的损伤，可以提高相关病灶的检测及诊断能力，并据此开发新的治疗方法[11 ⇓ ⇓ -14 ] .因此，发展无创活体代谢MRI技术对代谢异常疾病的研究具有十分重要的意义. ...
Gradient coils in permanent magnet miniature magnetic resonance imagers and image quality
1
2012
... 磁共振成像（Magnetic Resonance Imaging，MRI）作为一种无辐射和非侵入影像技术，已成为生物医学研究以及临床诊断的重要工具[1 ⇓ ⇓ -4 ] .其中，高场小动物MRI是一个重要分支，它具有更高的磁场强度和梯度强度，能够实现更高的空间和时间分辨率，使MRI达到分子影像水平.常规1 H MRI主要提供生物体组织结构像信息[5 ] ，13 C、23 Na等杂核MRI能够提供更丰富的生理和代谢功能信息[6 ⇓ ⇓ ⇓ -10 ] .准确测量胶质瘤、认知障碍和中风等代谢异常疾病的损伤，可以提高相关病灶的检测及诊断能力，并据此开发新的治疗方法[11 ⇓ ⇓ -14 ] .因此，发展无创活体代谢MRI技术对代谢异常疾病的研究具有十分重要的意义. ...
永磁微型磁共振成像仪的梯度线圈与图像质量
1
2012
... 磁共振成像（Magnetic Resonance Imaging，MRI）作为一种无辐射和非侵入影像技术，已成为生物医学研究以及临床诊断的重要工具[1 ⇓ ⇓ -4 ] .其中，高场小动物MRI是一个重要分支，它具有更高的磁场强度和梯度强度，能够实现更高的空间和时间分辨率，使MRI达到分子影像水平.常规1 H MRI主要提供生物体组织结构像信息[5 ] ，13 C、23 Na等杂核MRI能够提供更丰富的生理和代谢功能信息[6 ⇓ ⇓ ⇓ -10 ] .准确测量胶质瘤、认知障碍和中风等代谢异常疾病的损伤，可以提高相关病灶的检测及诊断能力，并据此开发新的治疗方法[11 ⇓ ⇓ -14 ] .因此，发展无创活体代谢MRI技术对代谢异常疾病的研究具有十分重要的意义. ...
Impact of cannabis use on brain metabolism using 31 P and 1 H magnetic resonance spectroscopy
1
2023
... 磁共振成像（Magnetic Resonance Imaging，MRI）作为一种无辐射和非侵入影像技术，已成为生物医学研究以及临床诊断的重要工具[1 ⇓ ⇓ -4 ] .其中，高场小动物MRI是一个重要分支，它具有更高的磁场强度和梯度强度，能够实现更高的空间和时间分辨率，使MRI达到分子影像水平.常规1 H MRI主要提供生物体组织结构像信息[5 ] ，13 C、23 Na等杂核MRI能够提供更丰富的生理和代谢功能信息[6 ⇓ ⇓ ⇓ -10 ] .准确测量胶质瘤、认知障碍和中风等代谢异常疾病的损伤，可以提高相关病灶的检测及诊断能力，并据此开发新的治疗方法[11 ⇓ ⇓ -14 ] .因此，发展无创活体代谢MRI技术对代谢异常疾病的研究具有十分重要的意义. ...
Hyperpolarized carbon 13 MRI: clinical applications and future directions in oncology
1
2023
... 磁共振成像（Magnetic Resonance Imaging，MRI）作为一种无辐射和非侵入影像技术，已成为生物医学研究以及临床诊断的重要工具[1 ⇓ ⇓ -4 ] .其中，高场小动物MRI是一个重要分支，它具有更高的磁场强度和梯度强度，能够实现更高的空间和时间分辨率，使MRI达到分子影像水平.常规1 H MRI主要提供生物体组织结构像信息[5 ] ，13 C、23 Na等杂核MRI能够提供更丰富的生理和代谢功能信息[6 ⇓ ⇓ ⇓ -10 ] .准确测量胶质瘤、认知障碍和中风等代谢异常疾病的损伤，可以提高相关病灶的检测及诊断能力，并据此开发新的治疗方法[11 ⇓ ⇓ -14 ] .因此，发展无创活体代谢MRI技术对代谢异常疾病的研究具有十分重要的意义. ...
Overview and progress of X-nuclei magnetic resonance imaging in biomedical studies
1
2023
... 磁共振成像（Magnetic Resonance Imaging，MRI）作为一种无辐射和非侵入影像技术，已成为生物医学研究以及临床诊断的重要工具[1 ⇓ ⇓ -4 ] .其中，高场小动物MRI是一个重要分支，它具有更高的磁场强度和梯度强度，能够实现更高的空间和时间分辨率，使MRI达到分子影像水平.常规1 H MRI主要提供生物体组织结构像信息[5 ] ，13 C、23 Na等杂核MRI能够提供更丰富的生理和代谢功能信息[6 ⇓ ⇓ ⇓ -10 ] .准确测量胶质瘤、认知障碍和中风等代谢异常疾病的损伤，可以提高相关病灶的检测及诊断能力，并据此开发新的治疗方法[11 ⇓ ⇓ -14 ] .因此，发展无创活体代谢MRI技术对代谢异常疾病的研究具有十分重要的意义. ...
Quantitative sodium (23 Na) MRI in pediatric gliomas: initial experience
1
2022
... 磁共振成像（Magnetic Resonance Imaging，MRI）作为一种无辐射和非侵入影像技术，已成为生物医学研究以及临床诊断的重要工具[1 ⇓ ⇓ -4 ] .其中，高场小动物MRI是一个重要分支，它具有更高的磁场强度和梯度强度，能够实现更高的空间和时间分辨率，使MRI达到分子影像水平.常规1 H MRI主要提供生物体组织结构像信息[5 ] ，13 C、23 Na等杂核MRI能够提供更丰富的生理和代谢功能信息[6 ⇓ ⇓ ⇓ -10 ] .准确测量胶质瘤、认知障碍和中风等代谢异常疾病的损伤，可以提高相关病灶的检测及诊断能力，并据此开发新的治疗方法[11 ⇓ ⇓ -14 ] .因此，发展无创活体代谢MRI技术对代谢异常疾病的研究具有十分重要的意义. ...
Dynamic perfluorinated gas MRI shows improved lung ventilation in people with cystic fibrosis after elexacaftor/tezacaftor/ivacaftor: an observational study
1
2022
... 磁共振成像（Magnetic Resonance Imaging，MRI）作为一种无辐射和非侵入影像技术，已成为生物医学研究以及临床诊断的重要工具[1 ⇓ ⇓ -4 ] .其中，高场小动物MRI是一个重要分支，它具有更高的磁场强度和梯度强度，能够实现更高的空间和时间分辨率，使MRI达到分子影像水平.常规1 H MRI主要提供生物体组织结构像信息[5 ] ，13 C、23 Na等杂核MRI能够提供更丰富的生理和代谢功能信息[6 ⇓ ⇓ ⇓ -10 ] .准确测量胶质瘤、认知障碍和中风等代谢异常疾病的损伤，可以提高相关病灶的检测及诊断能力，并据此开发新的治疗方法[11 ⇓ ⇓ -14 ] .因此，发展无创活体代谢MRI技术对代谢异常疾病的研究具有十分重要的意义. ...
Defining the conditions for the development of the emerging class of Fe(III)-based MRI contrast agents
1
2021
... 磁共振成像（Magnetic Resonance Imaging，MRI）作为一种无辐射和非侵入影像技术，已成为生物医学研究以及临床诊断的重要工具[1 ⇓ ⇓ -4 ] .其中，高场小动物MRI是一个重要分支，它具有更高的磁场强度和梯度强度，能够实现更高的空间和时间分辨率，使MRI达到分子影像水平.常规1 H MRI主要提供生物体组织结构像信息[5 ] ，13 C、23 Na等杂核MRI能够提供更丰富的生理和代谢功能信息[6 ⇓ ⇓ ⇓ -10 ] .准确测量胶质瘤、认知障碍和中风等代谢异常疾病的损伤，可以提高相关病灶的检测及诊断能力，并据此开发新的治疗方法[11 ⇓ ⇓ -14 ] .因此，发展无创活体代谢MRI技术对代谢异常疾病的研究具有十分重要的意义. ...
The principle of pH imaging with MR and its research progress on the formation mechanism and development of tumor acidic microenvironment
1
2021
... 磁共振成像（Magnetic Resonance Imaging，MRI）作为一种无辐射和非侵入影像技术，已成为生物医学研究以及临床诊断的重要工具[1 ⇓ ⇓ -4 ] .其中，高场小动物MRI是一个重要分支，它具有更高的磁场强度和梯度强度，能够实现更高的空间和时间分辨率，使MRI达到分子影像水平.常规1 H MRI主要提供生物体组织结构像信息[5 ] ，13 C、23 Na等杂核MRI能够提供更丰富的生理和代谢功能信息[6 ⇓ ⇓ ⇓ -10 ] .准确测量胶质瘤、认知障碍和中风等代谢异常疾病的损伤，可以提高相关病灶的检测及诊断能力，并据此开发新的治疗方法[11 ⇓ ⇓ -14 ] .因此，发展无创活体代谢MRI技术对代谢异常疾病的研究具有十分重要的意义. ...
磁共振pH成像原理及其在肿瘤酸性微环境形成机制及其发展演变中的研究进展
1
2021
... 磁共振成像（Magnetic Resonance Imaging，MRI）作为一种无辐射和非侵入影像技术，已成为生物医学研究以及临床诊断的重要工具[1 ⇓ ⇓ -4 ] .其中，高场小动物MRI是一个重要分支，它具有更高的磁场强度和梯度强度，能够实现更高的空间和时间分辨率，使MRI达到分子影像水平.常规1 H MRI主要提供生物体组织结构像信息[5 ] ，13 C、23 Na等杂核MRI能够提供更丰富的生理和代谢功能信息[6 ⇓ ⇓ ⇓ -10 ] .准确测量胶质瘤、认知障碍和中风等代谢异常疾病的损伤，可以提高相关病灶的检测及诊断能力，并据此开发新的治疗方法[11 ⇓ ⇓ -14 ] .因此，发展无创活体代谢MRI技术对代谢异常疾病的研究具有十分重要的意义. ...
Construction and evaluation of a switch-tuned 13 C-1 H birdcage radiofrequency coil for imaging the metabolism of hyperpolarized 13 C-enriched compounds
1
2014
... 磁共振成像（Magnetic Resonance Imaging，MRI）作为一种无辐射和非侵入影像技术，已成为生物医学研究以及临床诊断的重要工具[1 ⇓ ⇓ -4 ] .其中，高场小动物MRI是一个重要分支，它具有更高的磁场强度和梯度强度，能够实现更高的空间和时间分辨率，使MRI达到分子影像水平.常规1 H MRI主要提供生物体组织结构像信息[5 ] ，13 C、23 Na等杂核MRI能够提供更丰富的生理和代谢功能信息[6 ⇓ ⇓ ⇓ -10 ] .准确测量胶质瘤、认知障碍和中风等代谢异常疾病的损伤，可以提高相关病灶的检测及诊断能力，并据此开发新的治疗方法[11 ⇓ ⇓ -14 ] .因此，发展无创活体代谢MRI技术对代谢异常疾病的研究具有十分重要的意义. ...
A carbon-13 in viva double surface-coil NMR probe with efficient
1
1986
... 磁共振成像（Magnetic Resonance Imaging，MRI）作为一种无辐射和非侵入影像技术，已成为生物医学研究以及临床诊断的重要工具[1 ⇓ ⇓ -4 ] .其中，高场小动物MRI是一个重要分支，它具有更高的磁场强度和梯度强度，能够实现更高的空间和时间分辨率，使MRI达到分子影像水平.常规1 H MRI主要提供生物体组织结构像信息[5 ] ，13 C、23 Na等杂核MRI能够提供更丰富的生理和代谢功能信息[6 ⇓ ⇓ ⇓ -10 ] .准确测量胶质瘤、认知障碍和中风等代谢异常疾病的损伤，可以提高相关病灶的检测及诊断能力，并据此开发新的治疗方法[11 ⇓ ⇓ -14 ] .因此，发展无创活体代谢MRI技术对代谢异常疾病的研究具有十分重要的意义. ...
Progress in hyperpolarization 13 C magnetic resonance imaging of glioma
1
2022
... 磁共振成像（Magnetic Resonance Imaging，MRI）作为一种无辐射和非侵入影像技术，已成为生物医学研究以及临床诊断的重要工具[1 ⇓ ⇓ -4 ] .其中，高场小动物MRI是一个重要分支，它具有更高的磁场强度和梯度强度，能够实现更高的空间和时间分辨率，使MRI达到分子影像水平.常规1 H MRI主要提供生物体组织结构像信息[5 ] ，13 C、23 Na等杂核MRI能够提供更丰富的生理和代谢功能信息[6 ⇓ ⇓ ⇓ -10 ] .准确测量胶质瘤、认知障碍和中风等代谢异常疾病的损伤，可以提高相关病灶的检测及诊断能力，并据此开发新的治疗方法[11 ⇓ ⇓ -14 ] .因此，发展无创活体代谢MRI技术对代谢异常疾病的研究具有十分重要的意义. ...
脑胶质瘤超极化13 C-MRI研究进展
1
2022
... 磁共振成像（Magnetic Resonance Imaging，MRI）作为一种无辐射和非侵入影像技术，已成为生物医学研究以及临床诊断的重要工具[1 ⇓ ⇓ -4 ] .其中，高场小动物MRI是一个重要分支，它具有更高的磁场强度和梯度强度，能够实现更高的空间和时间分辨率，使MRI达到分子影像水平.常规1 H MRI主要提供生物体组织结构像信息[5 ] ，13 C、23 Na等杂核MRI能够提供更丰富的生理和代谢功能信息[6 ⇓ ⇓ ⇓ -10 ] .准确测量胶质瘤、认知障碍和中风等代谢异常疾病的损伤，可以提高相关病灶的检测及诊断能力，并据此开发新的治疗方法[11 ⇓ ⇓ -14 ] .因此，发展无创活体代谢MRI技术对代谢异常疾病的研究具有十分重要的意义. ...
1 H-13 C independently tuned radiofrequency surface coil applied for in vivo hyperpolarized MRI
1
2016
... 13 C同位素较低的天然丰度（仅为1.1%）和较低的旋磁比（约为1 H旋磁比的1/4）等固有物理性质导致13 C的磁共振信号信噪比较低；对于23 Na等快速弛豫的杂核MRI，T 2 弛豫时间很短，信号采集窗口狭窄，难以快速且精确地获得符合诊断需求的磁共振代谢图像[15 ⇓ ⇓ ⇓ -19 ] .因此，对于小口径小动物成像系统，获取高信噪比和高分辨率的13 C等杂核磁共振代谢图像对磁共振系统的硬件设备要求较高，一方面需要高切换率和高线性度梯度线圈系统进行MRI空间编码，用于提高MRI图像分辨率以及定位精度；另一方面需要设计高灵敏度的磁共振射频线圈，用于提高磁共振信号采集的信噪比，实现快速获取13 C等杂核代谢信息的功能.然而，目前商用的杂核小动物成像线圈和梯度系统通常需要定制，导致部件生产和维修周期长，同时用于小动物MRI的整机设备几乎被国外厂商垄断，使得仪器价格昂贵，国内开展相关研究的单位依然很少，这些因素都严重制约了MRI代谢成像这一重要研究方向的发展.在这种情况下，自主研制高场谱仪小动物杂核MRI代谢成像系统及关键部件就显得尤为重要，相关设备的研制对提高研究效率，减少科研成本，降低小动物MRI研究门槛以及推动相关生物医学研究发展都具有重要意义. ...
Coil profile estimation strategies for parallel imaging with hyperpolarized 13 C MRI
1
2019
... 13 C同位素较低的天然丰度（仅为1.1%）和较低的旋磁比（约为1 H旋磁比的1/4）等固有物理性质导致13 C的磁共振信号信噪比较低；对于23 Na等快速弛豫的杂核MRI，T 2 弛豫时间很短，信号采集窗口狭窄，难以快速且精确地获得符合诊断需求的磁共振代谢图像[15 ⇓ ⇓ ⇓ -19 ] .因此，对于小口径小动物成像系统，获取高信噪比和高分辨率的13 C等杂核磁共振代谢图像对磁共振系统的硬件设备要求较高，一方面需要高切换率和高线性度梯度线圈系统进行MRI空间编码，用于提高MRI图像分辨率以及定位精度；另一方面需要设计高灵敏度的磁共振射频线圈，用于提高磁共振信号采集的信噪比，实现快速获取13 C等杂核代谢信息的功能.然而，目前商用的杂核小动物成像线圈和梯度系统通常需要定制，导致部件生产和维修周期长，同时用于小动物MRI的整机设备几乎被国外厂商垄断，使得仪器价格昂贵，国内开展相关研究的单位依然很少，这些因素都严重制约了MRI代谢成像这一重要研究方向的发展.在这种情况下，自主研制高场谱仪小动物杂核MRI代谢成像系统及关键部件就显得尤为重要，相关设备的研制对提高研究效率，减少科研成本，降低小动物MRI研究门槛以及推动相关生物医学研究发展都具有重要意义. ...
RF coil design for accurate parallel imaging on 13 C MRSI using 23 Na sensitivity profiles
1
2022
... 13 C同位素较低的天然丰度（仅为1.1%）和较低的旋磁比（约为1 H旋磁比的1/4）等固有物理性质导致13 C的磁共振信号信噪比较低；对于23 Na等快速弛豫的杂核MRI，T 2 弛豫时间很短，信号采集窗口狭窄，难以快速且精确地获得符合诊断需求的磁共振代谢图像[15 ⇓ ⇓ ⇓ -19 ] .因此，对于小口径小动物成像系统，获取高信噪比和高分辨率的13 C等杂核磁共振代谢图像对磁共振系统的硬件设备要求较高，一方面需要高切换率和高线性度梯度线圈系统进行MRI空间编码，用于提高MRI图像分辨率以及定位精度；另一方面需要设计高灵敏度的磁共振射频线圈，用于提高磁共振信号采集的信噪比，实现快速获取13 C等杂核代谢信息的功能.然而，目前商用的杂核小动物成像线圈和梯度系统通常需要定制，导致部件生产和维修周期长，同时用于小动物MRI的整机设备几乎被国外厂商垄断，使得仪器价格昂贵，国内开展相关研究的单位依然很少，这些因素都严重制约了MRI代谢成像这一重要研究方向的发展.在这种情况下，自主研制高场谱仪小动物杂核MRI代谢成像系统及关键部件就显得尤为重要，相关设备的研制对提高研究效率，减少科研成本，降低小动物MRI研究门槛以及推动相关生物医学研究发展都具有重要意义. ...
A cryogenic 14-channel 13 C receiver array for 3 T human head imaging
1
2023
... 13 C同位素较低的天然丰度（仅为1.1%）和较低的旋磁比（约为1 H旋磁比的1/4）等固有物理性质导致13 C的磁共振信号信噪比较低；对于23 Na等快速弛豫的杂核MRI，T 2 弛豫时间很短，信号采集窗口狭窄，难以快速且精确地获得符合诊断需求的磁共振代谢图像[15 ⇓ ⇓ ⇓ -19 ] .因此，对于小口径小动物成像系统，获取高信噪比和高分辨率的13 C等杂核磁共振代谢图像对磁共振系统的硬件设备要求较高，一方面需要高切换率和高线性度梯度线圈系统进行MRI空间编码，用于提高MRI图像分辨率以及定位精度；另一方面需要设计高灵敏度的磁共振射频线圈，用于提高磁共振信号采集的信噪比，实现快速获取13 C等杂核代谢信息的功能.然而，目前商用的杂核小动物成像线圈和梯度系统通常需要定制，导致部件生产和维修周期长，同时用于小动物MRI的整机设备几乎被国外厂商垄断，使得仪器价格昂贵，国内开展相关研究的单位依然很少，这些因素都严重制约了MRI代谢成像这一重要研究方向的发展.在这种情况下，自主研制高场谱仪小动物杂核MRI代谢成像系统及关键部件就显得尤为重要，相关设备的研制对提高研究效率，减少科研成本，降低小动物MRI研究门槛以及推动相关生物医学研究发展都具有重要意义. ...
Protein in-cell NMR spectroscopy at 1.2 GHz
1
2021
... 13 C同位素较低的天然丰度（仅为1.1%）和较低的旋磁比（约为1 H旋磁比的1/4）等固有物理性质导致13 C的磁共振信号信噪比较低；对于23 Na等快速弛豫的杂核MRI，T 2 弛豫时间很短，信号采集窗口狭窄，难以快速且精确地获得符合诊断需求的磁共振代谢图像[15 ⇓ ⇓ ⇓ -19 ] .因此，对于小口径小动物成像系统，获取高信噪比和高分辨率的13 C等杂核磁共振代谢图像对磁共振系统的硬件设备要求较高，一方面需要高切换率和高线性度梯度线圈系统进行MRI空间编码，用于提高MRI图像分辨率以及定位精度；另一方面需要设计高灵敏度的磁共振射频线圈，用于提高磁共振信号采集的信噪比，实现快速获取13 C等杂核代谢信息的功能.然而，目前商用的杂核小动物成像线圈和梯度系统通常需要定制，导致部件生产和维修周期长，同时用于小动物MRI的整机设备几乎被国外厂商垄断，使得仪器价格昂贵，国内开展相关研究的单位依然很少，这些因素都严重制约了MRI代谢成像这一重要研究方向的发展.在这种情况下，自主研制高场谱仪小动物杂核MRI代谢成像系统及关键部件就显得尤为重要，相关设备的研制对提高研究效率，减少科研成本，降低小动物MRI研究门槛以及推动相关生物医学研究发展都具有重要意义. ...
Smoothed finite element methods (S-FEM): an overview and recent developments
1
2018
... 针对以上问题，本文根据自主研制的5 T小动物MRI谱仪系统和小动物13 C代谢MRI检测需求，从梯度线圈和射频线圈出发，设计了基于有限差分流函数方法的小口径梯度线圈（外径51 mm，内径37 mm），以及适用于小口径下1 H/13 C双共振射频线圈（外径36 mm，内径30 mm）.本文采用有限元方法（finite element method，FEM）对设计的梯度线圈以及射频线圈进行了数值模拟[20 ] ，并在自主研制的5 T MRI系统平台对线圈性能进行了验证，成功获取到了13 C标记的尿素水溶液样品的13 C MRI图像和小鼠头部的1 H MRI解剖结构像，实验结果显示利用本文研制的梯度线圈和射频线圈在小口径磁体下进行1 H/13 C MRI实验具有可行性. ...
Methods: of stream functions and thin wires: an intuitive approach to gradient coil design
1
2021
... 梯度线圈的设计方法主要分为两大类：一种是基于离散电流技术的方法，另一种是基于连续电流的方法[21 ] .基于离散电流技术的方法实施起来比较简单，但优化过程比较耗时；基于连续电流的方法的精度相对较高[22 ] .本文采用基于连续电流方法的有限差分流函数方法对小口径梯度线圈进行设计. ...
2
2021
... 梯度线圈的设计方法主要分为两大类：一种是基于离散电流技术的方法，另一种是基于连续电流的方法[21 ] .基于离散电流技术的方法实施起来比较简单，但优化过程比较耗时；基于连续电流的方法的精度相对较高[22 ] .本文采用基于连续电流方法的有限差分流函数方法对小口径梯度线圈进行设计. ...
... 对实测的磁场分布结果进行线性拟合后处理可以得到梯度线圈的效率和线性度，利用数字万用表测量制作的梯度线圈的电感和电阻.对于梯度线圈的切换率SR,可由下式求得[22 ] ： ...
Theory of gradient coil design methods for magnetic resonance imaging
1
2010
... 对于纵向超导磁体其磁场方向为腔体轴向方向，在如图1(a) 柱面坐标系下，根据圆筒型梯度线圈的几何特征，线圈圆柱面上的电流密度可以表示为$J(r)={{J}_{z}}{{e}_{z}}+{{J}_{\theta }}{{e}_{\theta }}$ ${{J}_{z}}$ ${{J}_{\theta }}$ z 轴方向电流密度和周向电流密度，图1(a) 中圆柱面内部的目标磁场区域内的点在直角坐标系下的坐标值可以用${{r}_{f}}({{x}_{f}},{{y}_{f}},{{z}_{f}})$ [23 ] ，对于任何一个目标磁场区域内的点，将主磁场方向定义为z 轴方向，则主磁场方向分量可以表示为： ...
Gradient coil design with enhanced shielding constraint for a cryogen-free superconducting MRI system
1
2024
... 其中，${{\mu }_{0}}$ Q 和S 为定义的中间表达式，R 为线圈圆柱面的底面半径，θ 为圆柱面上的网格节点在柱坐标下的角度值，zs为网格节点的z 轴高度变量，l 为线圈圆柱面高度.圆柱面上的网格节点顺序可以按展开为矩形面上的网格如图1(b) 和图1(c) 所示，从而使用圆柱面上的有限差分网格建立电流密度与电流密度流函数之间的关系[24 ] .图1 为梯度线圈圆柱面有限差分网格划分示意图. ...
Stream function approach for determining optimal surface currents
1
2003
... 根据流函数的定义[25 ] ，可得网格节点电流密度流函数Ψ和网格节点电流密度J 的有限差分关系： ...
Tikhonov regularization of a second order dynamical system with Hessian driven damping
1
2021
... 通过构造约束矩阵和采用Tikhonov正则化方法即可求解方程组，由于(6)式为病态方程组，采用Tikhonov正则化方法可求得近似解[26 ] ，Tikhonov正则化方法的一般形式为： ...
1
2021
... 常见的射频线圈有鸟笼线圈、马鞍线圈、表面线圈和阵列线圈，其中鸟笼线圈的射频场均匀性较好，马鞍线圈次之，但二者的灵敏度相对较低，表面线圈在牺牲射频场均匀性的前提下具有较高的检测灵敏度，阵列线圈兼顾较好的射频场均匀性和较高的检测灵敏度，具有良好的射频性能，但阵列线圈实现起来相对较为复杂[27 ] .本文选择马鞍线圈和表面线圈作为射频线圈的设计方案. ...
Comparing saddle, slotted-tube and parallel-plate coils for magnetic resonance imaging
1
2014
... 马鞍线圈作为结构简单且射频场相对均匀的线圈设计方案[28 ] ，如图5(a) 所示，假设其圆弧半径为a ，线圈长度为l ，则当线圈长度与圆弧半径的比值l /a =3.322，线圈开角为60˚时，可在线圈中心获得均匀度最好的磁场[29 ] . ...
Optimum geometry of saddle shaped coils for generating a uniform magnetic field
1
1970
... 马鞍线圈作为结构简单且射频场相对均匀的线圈设计方案[28 ] ，如图5(a) 所示，假设其圆弧半径为a ，线圈长度为l ，则当线圈长度与圆弧半径的比值l /a =3.322，线圈开角为60˚时，可在线圈中心获得均匀度最好的磁场[29 ] . ...
Lowest mutual coupling between closely spaced loop antennas
1
1991
... 如图5(b) 所示，表面线圈作为最简单的线圈结构，其磁场分布根据毕奥萨伐尔定律，圆形表面线圈产生的磁场可以表示为[30 ] ： ...
Developing an AI-empowered head-only ultra-high-performance gradient MRI system for high spatiotemporal neuroimaging
1
2024
... T rise 为上升下降沿时间，本文系统设置的T rise 为82 μs，实际成像实验先用1 H核对梯度线圈最大梯度G max 进行标定，使成像尺寸与实际相符，成像实验将在第3节详细描述.通过以上测试方法测得梯度线圈相关性能参数如表1 所示，从表中可以看出实际的梯度线圈具有良好的线性度，x 、y 、z 三个方向分别为0.999 51、0.997 58、0.999 78，满足成像需求的梯度线性度要求大于等于95%，因此本文设计的梯度线圈满足实际成像需求.同时由于线圈口径较小，G max 也超过了0.8 T/m，根据该梯度强度计算出x 、y 、z 三个方向实际使用的切换率分别为10 000 T/m/s、9 756.1 T/m/s、12 195.1 T/m/s.最大梯度强度数值是商用人体MRI系统平台（G max <0.1 T/m）的10倍左右，同时目前文献中报道的商用小动物MRI和人体头部MRI系统的最大SR分别为4 200 T/m/s（口径300 mm）和600 T/m/s（口径390 mm）[31 ,32 ] ，相对于小动物和人体MRI系统，本文设计的小口径梯度线圈系统（口径37 mm）能够实现更高SR的13 C磁共振代谢成像研究. ...
1
2019
... T rise 为上升下降沿时间，本文系统设置的T rise 为82 μs，实际成像实验先用1 H核对梯度线圈最大梯度G max 进行标定，使成像尺寸与实际相符，成像实验将在第3节详细描述.通过以上测试方法测得梯度线圈相关性能参数如表1 所示，从表中可以看出实际的梯度线圈具有良好的线性度，x 、y 、z 三个方向分别为0.999 51、0.997 58、0.999 78，满足成像需求的梯度线性度要求大于等于95%，因此本文设计的梯度线圈满足实际成像需求.同时由于线圈口径较小，G max 也超过了0.8 T/m，根据该梯度强度计算出x 、y 、z 三个方向实际使用的切换率分别为10 000 T/m/s、9 756.1 T/m/s、12 195.1 T/m/s.最大梯度强度数值是商用人体MRI系统平台（G max <0.1 T/m）的10倍左右，同时目前文献中报道的商用小动物MRI和人体头部MRI系统的最大SR分别为4 200 T/m/s（口径300 mm）和600 T/m/s（口径390 mm）[31 ,32 ] ，相对于小动物和人体MRI系统，本文设计的小口径梯度线圈系统（口径37 mm）能够实现更高SR的13 C磁共振代谢成像研究. ...
