一种提高核磁共振快弛豫信号测量精度的方法

doi:10.11938/cjmr20233082

一种提高核磁共振快弛豫信号测量精度的方法

马莹颖, 张宫^,^*, 廖中枢

长江大学油气资源与勘探技术教育部重点实验室，湖北武汉 430100

A Method for Improving the Measurement Accuracy of Nuclear Magnetic Resonance Fast Relaxation Signal

MA Yingying, ZHANG Gong^,^*, LIAO Zhongshu

Key Laboratory of Exploration Technologies for Oil and Gas Resources of Education Ministry, Yangtze University, Wuhan 430100, China

通讯作者: *Tel: 15652663116, E-mail:zhanggong@yangtzeu.edu.cn.

收稿日期: 2023-09-12 网络出版日期: 2023-10-10

基金资助:

湖北省重点研发计划资助项目(2020BAB094)

Corresponding authors: *Tel: 15652663116, E-mail:zhanggong@yangtzeu.edu.cn.

Received: 2023-09-12 Online: 2023-10-10

摘要

核磁共振技术能够直接探测样品中水、烃等含氢流体信号并对其含量及所处环境进行定量表征，广泛应用在油气勘探领域．在对页岩油气、致密油气等含有大量超快弛豫组分样品进行测量时，由于CPMG脉冲序列观测到的前端信号数据量过少导致测量信号不稳定，快弛豫组分结果可靠性较低．提出了多次微变回波间隔测量（MCTEM）的方法，在测量阶段加密了对核磁共振前端信号数据的采集，反演阶段采用了多次测量回波数据的联合反演，可以得到更加精确的快弛豫T₂谱．通过数值模拟和岩心物理实验对MCTEM方法进行了验证，结果显示MCTEM方法能够改善由回波间隔T_E偏高引起的T₂谱快弛豫组分峰消失的问题，可以有效提高快弛豫信号的测量精度．

关键词： 核磁共振; 测量精度; 多次微变回波间隔测量方法; 快弛豫组分

Abstract

Nuclear magnetic resonance (NMR) technology can directly detect hydrogen signals in hydrogen-containing fluids, such as water and hydrocarbon. It can provide quantitative characterization of the fluid content and surrounding environment, thus finding extensive application in oil and gas exploration field. However, when measured samples containing ultra-fast relaxation components, such as shale oil and gas, the reliability of measurement results tends to be very low because only a small number of front-end signals in Carr-Purcell-Meiboom-Gill (CPMG) pulse sequence can be obtained for the fast relaxation components. To address this problem, a multiple micro echo interval measurement (MCTEM) method was proposed in this research. In the measurement stage, the proposed method acquired more NMR front-end signals. In the inversion stage, multiple echo data were adopted for the joint inversion. It contributed to forming an accurate fast relaxation T₂ spectrum. MCTEM method was validated through numerical simulations and rock physics experiments. It was concluded from the results that MCTEM method could improve the problem of peak disappearance for fast relaxation components in T₂ spectrum caused by long echo interval. MCTEM method could enhance the measurement accuracy of fast relaxation signals effectively.

Keywords： NMR; measurement accuracy; multiple micro echo interval measurement; fast relaxation components

PDF (1061KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

马莹颖, 张宫, 廖中枢. 一种提高核磁共振快弛豫信号测量精度的方法[J]. 波谱学杂志, 2024, 41(2): 162-172 doi:10.11938/cjmr20233082

MA Yingying, ZHANG Gong, LIAO Zhongshu. A Method for Improving the Measurement Accuracy of Nuclear Magnetic Resonance Fast Relaxation Signal[J]. Chinese Journal of Magnetic Resonance, 2024, 41(2): 162-172 doi:10.11938/cjmr20233082

引言

近年来，随着对页岩油气等非常规资源勘探程度的加深，具有无损、非侵入等优势的核磁共振技术在非常规储层勘探开发中发挥着不可替代的作用^[1⇓-3].然而在测量含有快弛豫组分的页岩时，核磁共振技术面临诸多挑战.研究表明，岩心中的粘土束缚水、固体沥青或顺磁性物质会使横向弛豫时间缩短，使核磁共振测量得到的孔隙度减小^[4,5].泥页岩储层中的微裂缝会导致核磁共振T₂分布转换为孔径时产生误差^[6]. 常规储层计算渗透率时使用的平均T₂（SDR）模型或自由流体（Coates）模型不适用于由微纳米级孔隙及裂缝组成的页岩储层^[3].

除页岩本身特性外，仪器参数也会影响核磁共振测量结果，主要包括测量参数和信噪比.前人学者^[7,8]通过研究仪器主要测量参数对核磁共振结果的影响，发现核磁共振T₂谱对回波间隔T_E的变化敏感.回波间隔偏大时，快弛豫组分信息丢失，页岩核磁共振孔隙度测量值下降^[8⇓⇓-11].缩短T_E可以更早检测到快弛豫组分的核磁共振信号，但受限于脉冲长度、采集带宽、仪器性能，核磁共振岩心分析仪所用T_E很难达到测量超快弛豫组分的效果.减小T_E还会增强振铃效应，噪声极易造成回波串中首个回波采集点的幅度发生变化，从而严重影响T₂谱反演结果中的快弛豫部分信号^[11,12].

为提高核磁共振测量快弛豫信号的精度，提出一种多次微变回波间隔测量（Multiple micro echo interval measurement，MCTEM）的方法，在采集回波数据时通过微变T_E来增加核磁共振前端信号数据量，反演时对多回波数据进行联合反演，通过对模型、溶液、岩心等进行不同测量方法下的一维T₂核磁共振实验，证明了MCTEM方法在提高核磁共振实验设备对快弛豫组分测量精度方面的有效性.

1 核磁共振T₂谱测量

1.1 回波采集

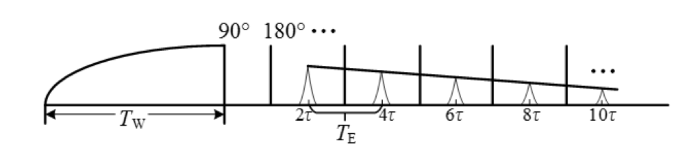
核磁共振岩心实验通常是在均匀磁场条件下利用CPMG脉冲序列测量横向弛豫时间T₂^[13].CPMG脉冲序列是由一个标准90˚脉冲和连续施加的一系列时间间隔相同（2τ）的180˚脉冲组成.90˚脉冲将磁化矢量扳转到横向平面上，质子群发生散相会引起自由感应衰减.在间隔时间τ后，施加180˚脉冲重新聚焦磁化矢量，产生的自旋回波被接收线圈记录.重复施加180˚脉冲，产生一系列自旋回波，回波间的时间为2τ，记为回波间隔T_E，如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 CPMG脉冲序列及自旋回波

Fig. 1 CPMG pulse sequence and spin echo

在均匀磁场、回波间隔不太大的情况下，扩散弛豫的影响可忽略不计.当等待时间T_W足够长时，测量的回波信号衰减规律满足下式^[14]：

(1)$b_{i}=\sum_{j=1}^{n} f_{j} \exp \left(-\frac{t_{i}}{T_{2 j}}\right) \quad i=1,2, \cdots, m$

式中， b_i表示t_i时刻测量的第i个回波的回波幅度； $T_{2j}$表示第j种弛豫分量对应的横向弛豫时间T₂；n为弛豫分量的个数；m为采集的每个回波串中包含的回波个数； $f_{j}$表示横向弛豫时间为$T_{2j}$时的信号量.

1.2 T₂谱反演

求解各弛豫分量对应f_j的过程称为反演.解方程(1)本质上是求解第一类Fredholm积分方程，这是一个非适定问题，常见的反演算法包括罚函数法、奇异值分解及其改进算法、非负最小二乘法等^[13].

以奇异值分解算法为例^[14]，(1)式可以写成矩阵形式：

(2)$A x=b$

式中，$\boldsymbol{b}=\left[b_{1}, b_{2}, \cdots, b_{m}\right]^{T} ; \quad \boldsymbol{x}=\left[f_{1}, f_{2}, \cdots, f_{n}\right]^{T} ; \quad \boldsymbol{A}=\left[\exp \left(-t_{i} / T_{2 j}\right)\right]_{m \times n}$.

(2)式两边同时左乘以逆矩阵$A^{-}$，可得：

(3)$\boldsymbol{x}=\boldsymbol{A}^{-} \boldsymbol{b}$

奇异值分解算法是基于矩阵的奇异值分解定理，假设A是$ m \times n $阶矩阵，当行数m大于等于列数n时，存在正交矩阵$\boldsymbol{U}_{m \times n}$，非负对角矩阵$\boldsymbol{W}_{m \times n}$以及正交矩阵$\boldsymbol{V}_{n \times n}$：

(4)$\boldsymbol{A}_{m \times n}=\boldsymbol{U}_{m \times m}\left[\operatorname{diag}\left(w_{j}\right)\right]_{m \times n} \boldsymbol{V}_{n \times n}^{T}$

式中，$w_{j} \geq 0(1 \leq j \leq n)$；U、V为正交矩阵.

求出系数矩阵A的广义逆矩阵并代入方程(3)，即可求得T₂分布的幅度值.

1.3 快弛豫组分受前端回波信号影响

在核磁共振实验过程中，若使用的T_E较大，岩心样品中沥青、干酪根等快弛豫组分（即弛豫时间较短的组分）的部分信号会在首个回波采集点前快速衰减，造成弛豫组分漏失（RCL）现象^[15].图2所示为实测饱水岩心在不同回波间隔下的T₂谱，结果表明T_E越大，快弛豫组分信息损失越多，所测得的核磁共振孔隙度值减小.

图2

新窗口打开| 下载原图ZIP| 生成PPT

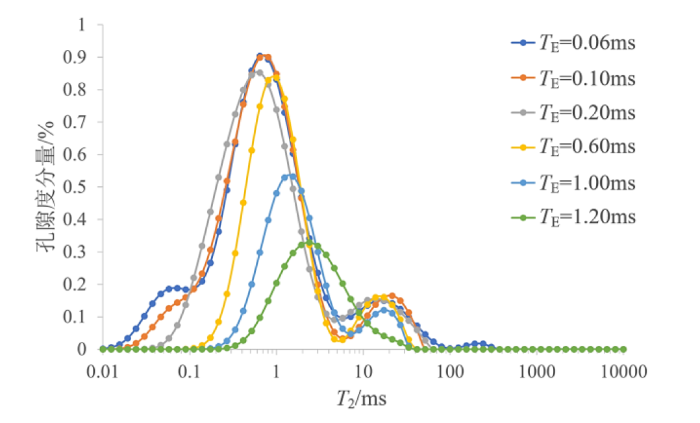
图2 饱水岩心在不同回波间隔下的T₂谱

Fig. 2 T₂ spectra obtained at different echo intervals for water-saturated sample

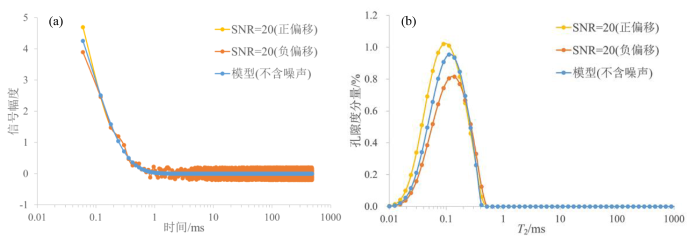
避免RCL现象的方法是减小T_E，但目前实验设备能达到的T_E下限为0.06 ms左右^[1]（对应可检测信号为T₂>0.15 ms的组分），快弛豫组分难以完全探测.而且在采集回波数据的过程中，首个回波点极易受噪声干扰，导致该点的信号幅度发生改变，首个回波的微小变化就会对前端信号产生严重扰动，从而影响快弛豫T₂谱幅度及核磁共振孔隙度计算.图3所示为模拟受噪声干扰的回波串及其T₂分布，结果显示，噪声会使回波串首点与实际位置产生偏移，这个偏移可能是正偏移，即回波串首点幅度高于实际幅度，也可能是负偏移，即回波串首点幅度低于实际幅度.同时也会干扰前几个回波采集点，导致其幅度上下波动，从而影响反演结果.随着信噪比降低，T₂谱幅度及峰值位置变化明显.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 快弛豫组分受噪声干扰的(a)回波串及其(b)T₂谱

Fig. 3 Echo trains (a) and T₂ spectrum (b) of fast relaxation component disturbed by noise

2 MCTEM方法

2.1 数据加密采集方法

为减小前端回波信号波动对快弛豫组分的影响，可以采用数据加密采集的方法补偿前端信号数据量过少的问题.在使用最小T_E（仪器允许范围内）采集一个完整的CPMG回波串的基础上，通过多次变化T_E测量具有不同弛豫组分的样品，并根据测量时间$t_{i}$与回波间隔T_E的关系（$t_{i}=i T_{\mathrm{E}}, i=1,2, \cdots, m$），将采集的多回波数据按照时间进行组合，达到提高前端信号质量的目的，如图4所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 加密采集回波数据示意图

Fig. 4 Diagram of increasing echo data acquisition density

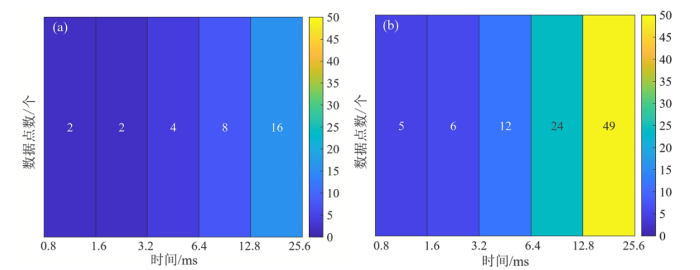
由图5可见，经过加密采集回波数据后，前端信号的数据点数增多.数据加密采集方法的目的是降低快弛豫信号对噪声的敏感性，从反演角度来说是使快弛豫T₂谱结果的可靠性更高，因此该方法对于页岩油气这类含有大量快弛豫组分信息的储层，具有较大的应用价值.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 原始回波数据点数(a)与加密回波数据点数(b)对比

Fig. 5 Comparison between raw echo data points (a) and increased echo data points (b)

2.2 基于加密采集的T₂谱反演

针对多回波数据的反演问题，借鉴了多回波串联合反演方法中拼接法的思路^[16]，将不同T_E下测量的多回波数据按照时间$t_{i}$的顺序排列，并对组合后的回波串进行联合反演．在给定足够长的等待时间T_W的前提下，假设测量不同T_E的回波串数据共s组，第1、2、s组回波串的回波幅度可分别表示为：

(5)$\left\{\begin{array}{c} b_{1 i_{\text {full }}}=\sum_{j=1}^{n} f_{j} \exp \left(-\frac{i_{\text {full }} T_{\mathrm{E} 1}}{T_{2 j}}\right)+\varepsilon_{1 i_{\text {tul }}} \quad\left(i_{\text {full }}=1,2, \cdots, m\right) \\ b_{2 i_{\text {part }}}=\sum_{j=1}^{n} f_{j} \exp \left(-\frac{i_{\text {part }} T_{\mathrm{E} 2}}{T_{2 j}}\right)+\varepsilon_{2 i_{\text {paat }}}\left(i_{\text {part }}=1,2, \cdots, k\right) \\ \vdots \\ b_{s i_{\text {pat }}}=\sum_{j=1}^{n} f_{j} \exp \left(-\frac{i_{\text {part }} T_{\mathrm{Es}}}{T_{2 j}}\right)+\varepsilon_{s i_{\text {part }}} \quad\left(i_{\text {part }}=1,2, \cdots, k\right) \end{array}\right.$

式中， $i_{full}$代表完整采集m个回波，$i_{part}$代表只采集前k个回波，$b_{si}$表示回波间隔为$T_{Es}$时第i个回波的幅度；n为横向弛豫时间$T_{2j}$的个数；$f_{j}$是关于横向弛豫时间为$T_{2j}$时的信号量； $\mathcal{E}_{s i}$表示回波间隔为$T_{Es}$时第i个回波的噪声.

上式可写成：

(6)$b_{r}=\sum_{j=1}^{n} f_{j} \exp \left(-\frac{t_{i}}{T_{2 j}}\right)+\varepsilon_{r} \quad(r=1,2, \cdots, m+(s-1) \times k)$

同样可将(6)式简化为：

(7)$\boldsymbol{A} \cdot \boldsymbol{F}=\boldsymbol{B}+\boldsymbol{E}$

(6)式的简化与(1)式简化为(2)式相同.矩阵A代表(6)式中的指数项，矩阵F代表方程中f_j，矩阵B代表方程中的b_r，矩阵E代表方程中的噪声项.(7)式中，$A_{r \times n}$为系数矩阵；$F_{n \times l}$为反演的T₂分布中弛豫时间是$T_{2j}$时对应的幅度；$B_{r \times l}$为测量的回波幅度；r为加密采集回波后的系数矩阵的行数.

通过T₂谱反演过程可知，对任意$t_{i}$时刻，只要存在对应的回波幅度$b_{i}$，就能求得各弛豫时间对应的信号幅度.与常规T₂谱反演相比，基于加密采集的T₂谱反演方法中系数矩阵的行数增加，列数保持不变，即T₂布点个数没有改变.对(7)式求解等价于实现多回波间隔数据联合反演.

3 方法验证

使用实验室自研的正反演模拟软件NMR Forward Inversion，基于对数坐标下的一维高斯分布函数分别构造了包含不同弛豫组分的双峰T₂谱^[17]，核磁共振总孔隙度为8%.图6为构建的模型，组分1的T₂中心值设置为0.8 ms，组分2的T₂中心值设置为10.0 ms，组分3的T₂中心值设置为26.0 ms.

图6

新窗口打开| 下载原图ZIP| 生成PPT

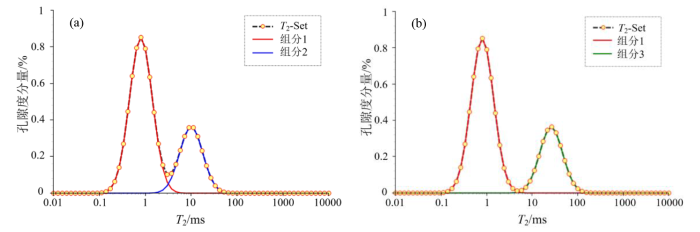
图6 数值模拟模型. (a)模型一；(b)模型二

Fig. 6 Numerical simulation models. (a) Model 1; (b) Model 2

模拟回波数据采集并增加高斯白噪声.采用T_W=4 000 ms进行多次微变回波间隔的回波采集，T_E分别设置为0.8、0.9、1.0、1.1、1.2、1.3、1.4、1.5 ms，回波个数N_ECH=2 000，将变T_E采集的回波数据进行多回波联合反演，与T_E=0.8 ms测量结果相比，T_E=0.1 ms测量结果作为参考标准.

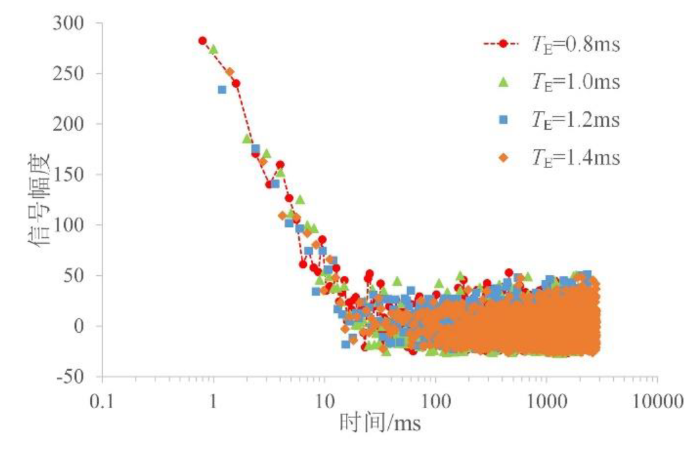
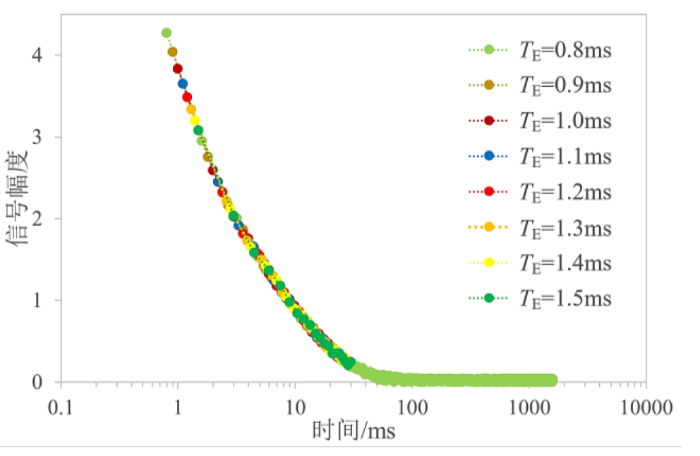
对于模型一，控制信噪比为100.图7所示为多次微变回波间隔采集的CPMG回波串，为节省数据存储空间，仅使用最小T_E采集完整的CPMG回波串，微变T_E并提取对应的前20个回波叠加到回波串中，再增加回波个数对反演结果无明显影响.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 多次微变回波间隔采集的CPMG回波串

Fig. 7 CPMG echo trains obtained by MCTEM

使用2.2节所述方法得到加密采集后的T₂谱，进一步，将T_E=0.1、0.8 ms采集的回波数据反演出T₂谱.图8所示为两个模型的数值模拟T₂分布.由图8(a)可见，T_E=0.8 ms测量结果由于T_E偏大，使不同流体组分的横向弛豫时间重叠，左、右峰区分度降低.MCTEM方法通过加密采集前端信号，T₂谱从单峰恢复为双峰，说明该方法在T_E较大的情况下可以采集部分快弛豫组分的信息.与T_E=0.1 ms测量结果相比，两种测量方法的右峰位置基本不变，MCTEM方法的左峰T₂中心值偏大，谱峰幅度降低.

图8

新窗口打开| 下载原图ZIP| 生成PPT

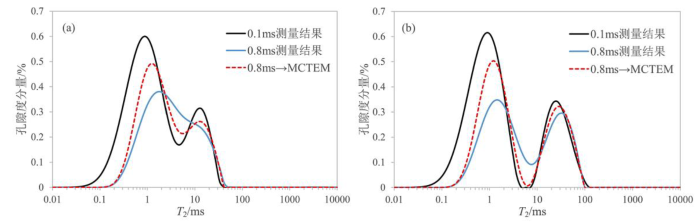
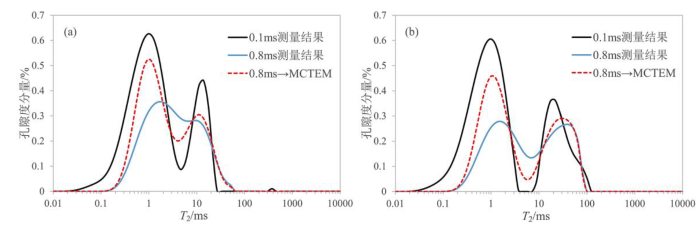
图8 信噪比为100时数值模拟T₂谱. (a)模型一；(b)模型二

Fig. 8 T₂ spectra obtained by numerical simulation at SNR=100. (a) Model 1; (b) Model 2

由图8(b)可见，不同测量方法的核磁共振谱峰区分度均较高，能够清晰分辨模型中包含两种流体组分，且右峰分布范围和幅度均无明显差异，说明增加回波间隔对较慢弛豫组分的影响小.对比T_E=0.1 ms测量结果，MCTEM方法的左峰中心右移，峰值降低.与T_E=0.8 ms测量结果相比，MCTEM方法测得的左峰中心位置和谱峰幅度与T_E=0.1 ms结果更接近.

采集参数不变，将信噪比降低为10，以验证提出的方法对低信噪比数据的适用性.图9所示为低信噪比条件下两个模型的数值模拟T₂分布.MCTEM方法与T_E=0.1 ms的左峰中心值相等，即获取组分1（左峰）弛豫信息的能力相同.对比图6中的预设T₂值，模型一中不同方法的右峰中心均向右移动，而模型二在T_E=0.1 ms回波间隔下的右峰中心则向左移动.表1为不同信噪比下两种模型的孔隙度数值模拟结果. 由表1可知，不同方法测量得到的孔隙度与理论标准均存在一定偏差，MCTEM方法比T_E=0.8 ms的误差要小，说明该方法能够减小噪声对反演结果的影响.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 信噪比为10时数值模拟T₂谱. (a)模型一；(b)模型二

Fig. 9 T₂ spectra obtained by numerical simulation at SNR=10. (a) Model 1; (b) Model 2

表1 不同信噪比下两种模型的数值模拟结果

Table 1 Numerical simulation results of two models at different SNR

模型名称		模型一				模型二
测量方法		理论标准	T_E=0.1 ms	T_E=0.8 ms	MCTEM	理论标准	T_E=0.1 ms	T_E=0.8 ms	MCTEM
高信噪比（100）	孔隙度/%	8.00	8.21	5.64	6.26	8.00	8.20	5.59	6.28
高信噪比（100）	绝对误差/%	0.00	0.21	2.36	1.74	0.00	0.20	2.41	1.72
低信噪比（10）	孔隙度/%	8.00	8.21	5.65	6.50	8.00	8.21	5.25	6.11
低信噪比（10）	绝对误差/%	0.00	0.21	2.35	1.50	0.00	0.21	2.75	1.89

新窗口打开| 下载CSV

4 实际应用

4.1 硫酸铜溶液实验

为与数值模拟构建的模型相匹配，进而验证MCTEM方法在提高快弛豫组分测量精度方面的效果，本文采用3组具有特定T₂的硫酸铜（CuSO₄）溶液，模拟两种具有不同流体组分的样品.通过配置2.00、0.15、0.08 mol/L等不同浓度的CuSO₄溶液，得到T₂分别为0.7、11.0、21.0 ms的三组溶液各0.5 mL，编号为A~C. 组合溶液A、B与溶液A、C得到1号和2号实验样品.

实验使用苏州纽迈公司生产的MesoMR23-060H-I核磁共振岩心分析仪（磁场强度为0.5 T，氢核共振频率为21 MHz），使用CPMG脉冲序列对样品进行T₂测量，测量温度统一设定为32 ℃，详细参数见表2.分别对上述两组样品依次进行MCTEM方法以及T_E=0.1 ms、T_E=0.8 ms的核磁共振实验并反演T₂谱.

表2 两组实验样品的核磁共振测量参数

Table 2 NMR measurement parameters for two samples

样品编号	体积/mL	模型T₂/ms	采集参数
样品编号	体积/mL	模型T₂/ms	等待时间/ms	扫描次数	回波间隔/ms	回波个数
1号	1.0	0.7、11.0	4000	1	0.1、0.8、0.9、1.0、1.1、1.2、1.3、1.4、1.5	2000
2号	1.0	0.7、21.0	4000	1	0.1、0.8、0.9、1.0、1.1、1.2、1.3、1.4、1.5	2000

新窗口打开| 下载CSV

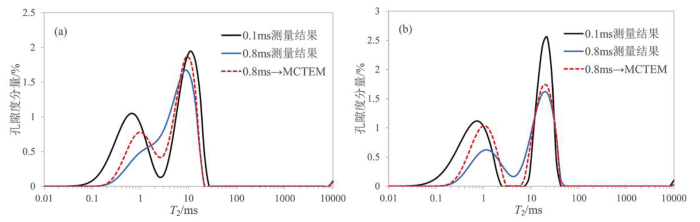
图10(a)所示为1号样品的核磁共振实验结果.由图可知，T_E=0.1 ms测量的核磁共振谱呈谱峰较为独立、左右峰区分明显的双峰分布，T_E=0.8 ms测量由于回波间隔较大，导致T₂谱形态由双峰变为近似单峰，两种流体组分弛豫峰的特征被掩盖.MCTEM方法可以对快弛豫组分峰进行恢复，证明该方法采集快弛豫组分信息的准确度较高.但与T_E=0.1 ms测量结果对比，MCTEM的核磁共振谱右峰中心值略微减小，左峰幅度降低且中心位置右移.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 信噪比高于200时核磁共振实验结果. (a) 1号样品；(b) 2号样品

Fig. 10 NMR experimental results obtained at high SNR(>200). (a) Sample 1; (b) Sample 2

图10(b)所示为2号样品的核磁共振实验结果.由图可知，不同测量方法的核磁共振T₂谱右峰位置不变，但T_E=0.1 ms测量的谱峰幅度更高.MCTEM方法获得的左峰中心值比模型T₂值（0.7 ms）大.比较T_E=0.8 ms测量和MCTEM方法的反演结果，两者的T₂谱均为双峰形态，体现了2号样品含有不同流体组分.左峰中心位置大致相同，但MCTEM方法的T₂谱形态及其幅度更接近T_E=0.1 ms测量结果.

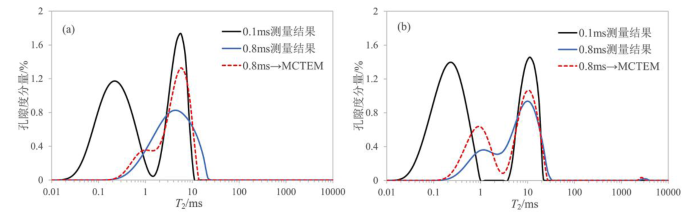
图11所示为两组样品在低信噪比条件下（SNR<30）的核磁共振实验结果.由图可知，低信噪比条件下，MCTEM方法测量的T₂谱仍可以反映样品具有两种流体组分.对比T_E=0.1 ms测量结果，由MCTEM方法获得的T₂谱右峰位置不变，左峰中心右移.与模型T₂值相比，两组样品在T_E=0.1 ms时的T₂谱均向左移，T₂缩短.理论上快弛豫组分峰的T₂值应为0.7 ms，实际中回波数据受信噪比等因素的影响，且反演时给定回波串首点的权重因子高，导致核磁共振谱左峰中心位于理论值的左边.MCTEM方法能够减弱高权重回波首点对噪声的敏感性，得到的谱峰位置准确度更高.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 信噪比低于30时核磁共振实验结果. (a) 1号样品；(b) 2号样品

Fig. 11 NMR experimental results obtained at low SNR(<30). (a) Sample 1; (b) Sample 2

4.2 真实岩心实验

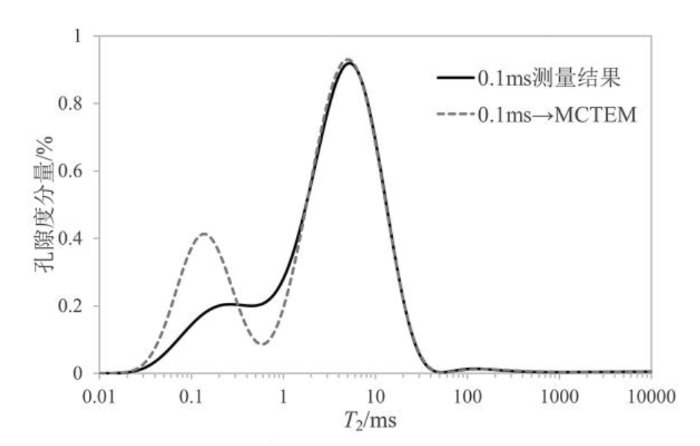
选取一块吉木萨尔芦草沟组典型页岩油储层岩心样品进行实验，将其制备成直径2.50 cm、高2.37 cm的柱塞样.对岩心原样使用CPMG脉冲序列采集T₂信息，回波间隔从0.1~0.19 ms以0.01 ms步长变化，其它采集参数同4.1节.图12所示为岩心核磁共振实验结果.由图可见，T_E=0.1 ms测量结果近似双峰形态，MCTEM方法得到的T₂谱呈谱峰较为独立、左右峰区分明显的双峰分布，不同测量结果中较慢弛豫组分的弛豫时间基本一致.T_E=0.1 ms测量的快弛豫组分峰不明显，原因是回波串首点幅度低于多次变化T_E测量的回波串首点幅度，从而导致T₂谱幅度降低.通过MCTEM采集多回波数据，并对多个回波的回波幅度进行平均，使快弛豫组分峰的幅度增加.该方法能区分岩心孔隙中含有两种流体组分，达到比T_E=0.1 ms更高的测量精度.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 岩心核磁共振实验结果

Fig. 12 NMR experimental results of rock sample

5 结论

本文通过数值模拟对MCTEM方法进行验证，并对硫酸铜溶液、岩心等样品进行不同方法下的一维T₂核磁共振实验，分析不同测量方法的T₂谱结果得到以下结论：

（1）MCTEM方法能够提高实验室核磁共振仪器对快弛豫组分的测量精度，一定程度上恢复由回波间隔偏高造成的快弛豫组分信息缺失，适用于页岩油气这类快弛豫组分较多的储层.

（2）对于不同样品，MCTEM方法对测量结果的影响并不相同.针对组分间T₂值差别较小的模型一或1号样品在常规测量方法中得到的左、右峰区分不明显的T₂谱结果，MCTEM方法可以恢复快弛豫峰特征，得到谱峰较为独立、左右峰区分明显的T₂谱，有利于进行后续的实验结果分析.

（3）低信噪比测量环境下，由于常规方法采集的前端信号数据点稀疏，受噪声影响的回波串首点幅度与实际位置发生偏移，导致T₂谱峰值中心改变.MCTEM方法降低了回波串首点对噪声的敏感程度，得到精度更高的快弛豫T₂谱.但MCTEM方法需测量不同T_E下的CPMG回波串，实验较为耗时，后续将会改进该方法.

利益冲突

无

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

WANG

Z Z

, LI

, WEI

Y X

, et al.

NMR technologies for evaluating oil & gas shale: a review

[J]. Chinese J Magn Reson, 2015, 32(4): 688-698.

[本文引用: 2]

王志战, 李新, 魏杨旭, 等.

页岩油气层核磁共振评价技术综述

[J]. 波谱学杂志, 2015, 32(4): 688-698.

DOI:10.11938/cjmr20150414 [本文引用: 2]

对于常规储层，核磁共振是一项十分有效的解释—评价技术，它既能评价岩石物性与孔隙结构，又能评价孔隙流体分布与饱和度，且具有快速、无损、经济等特点；而对于页岩储层，其核磁共振受纳米级孔隙、复杂矿物成分、特殊孔隙结构、较高有机质含量、超低渗透性及内部梯度和受限扩散等因素的影响，面临探测分辨率低、解释模型不适用等瓶颈．为了发挥该项技术在页岩油气勘探开发中的作用，将国内外的页岩油气层核磁共振分析、评价技术与相关的页岩油气层实验室微观分析成果相结合，进行了系统梳理，从探测分辨率的提高、孔隙结构与岩石物性评价模型的建立、孔隙流体分布与识别模型的建立等方面进行了综述，提出需加强纳米孔的核磁共振弛豫机理和提高 D-T2 二维谱分辨率两个基础研究，在此基础上，进一步完善岩石物理及孔隙流体两个评价模型．

[2]

SUN

Z L

, LI

Z M

, SHEN

B J

, et al.

NMR technology in reservoir evaluation for shale oil and gas

[J]. Petroleum Geology & Experiment, 2022, 44(5): 930-940.