基于开路谐振环的电子自旋共振系统设计与表征

doi:10.11938/cjmr20223018

基于开路谐振环的电子自旋共振系统设计与表征

骆培文¹, 汪伦², 吴喆¹, 张文旭^,²^,^*

1.电子科技大学物理学院，四川成都 611731

2.电子薄膜与集成器件国家重点实验室，电子科技大学，四川成都 611731

The Design and Characterization of Electron Spin Resonance Spectrometer Based on Double Split Ring Resonator

LUO Peiwen¹, WANG Lun², WU Zhe¹, ZHANG Wenxu^,²^,^*

1. School of Physics, University of Electronic Science and Technology of China, Chengdu 611731, China

2. State Key Laboratory of Electronic Thin Films and Integrated Devices, University of Electronic Science and Technology of China, Chengdu 611731, China

通讯作者: * Tel: 15561831603, E-mail:xwzhang@uestc.edu.cn.

收稿日期: 2022-08-29

基金资助:

四川省科技厅基金项目(2020YJ0266)

Corresponding authors: * Tel: 15561831603, E-mail:xwzhang@uestc.edu.cn.

Received: 2022-08-29

摘要

本文采用有限元电磁仿真设计了基于开路谐振环的微带线谐振器，并利用该谐振器搭建了电子自旋共振测试系统．该谐振器的3 dB带宽为58.7 MHz，且具有开放式的平面结构．对不同质量的二苯基三硝基苯肼（DPPH）样品测试结果显示本系统的室温自旋探测灵敏度可以达到9.66×10¹² spins/Gs Hz^1/2；对以微晶玻璃和硅片为基底的DPPH样品测试结果表明本系统能实现对大尺寸、高损耗样品的电子自旋共振信号的非破坏性测量．本系统为薄膜材料的缺陷研究以及相关的微波性能表征提供了便捷的手段．

关键词： 双开口环谐振器; 介电损耗; 薄膜; 电子自旋共振

Abstract

In this paper, a microstrip resonator based on double split rings is used to build an electron spin resonance (ESR) measurement system. The resonator is optimized by the finite element electromagnetic simulation and the 3 dB bandwidth is 58.7 MHz. Due to the open structure of the resonator, large-size samples with high dielectric loss can be measured nondestructively. The ESR signal of 2,2-diphenyl-1-picrylhydrazyl (DPPH) powder with different quality is measured at room temperature, and the result indicated that the spin detection limit of this system can reach 9.66 $\times$ 10¹² spins/Gs Hz^1/2. It is demonstrated that the system can be used to characterize films deposited on different substrates such as silicon, glasses or ceramics regardless of its high frequency losses through the measurement of DPPH sample spin-coated on silicon and zerodur. Our system provides a convenient approach to research the defect of thin films and to characterize their performances within microwave frequency.

Keywords： double split ring resonator; dielectric loss; thin film; electron spin resonance

PDF (835KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

骆培文, 汪伦, 吴喆, 张文旭. 基于开路谐振环的电子自旋共振系统设计与表征[J]. 波谱学杂志, 2023, 40(1): 92-99 doi:10.11938/cjmr20223018

LUO Peiwen. The Design and Characterization of Electron Spin Resonance Spectrometer Based on Double Split Ring Resonator[J]. Chinese Journal of Magnetic Resonance, 2023, 40(1): 92-99 doi:10.11938/cjmr20223018

引言

电子自旋共振（Electron Spin Resonance，ESR），又称电子顺磁共振（Electron Paramagnetic Resonance，EPR），是指当处于直流磁场中的未成对电子受到微波磁场作用，电子自旋的Larmor进动频率与激励的微波频率相等时，产生共振吸收的现象.ESR在生物、物理以及材料科学中有重要的应用^[1⇓⇓-4].在通常的ESR测试中，常采用X波段（8~12 GHz）金属谐振腔^[5]作为谐振单元，利用谐振腔在TE₀₁₁模式下产生的轴向微波磁场激励样品以获得ESR信号，其室温灵敏度（可探测到的最小自旋数）可以超过10¹¹ spins/Gs Hz^1/2（1 Gs = 10^-4 T）.然而受谐振腔腔体体积的限制，在ESR测试中，需要将样品尺寸限制在1 mm³以内以放入石英管中，这极大地限制了ESR在材料表征中的应用：比如不能同时对同一薄膜的自旋以及输运特性等其它特性进行表征；或者样品破坏后也可能无法根据ESR结果对同一样品进行进一步表征.在近年的研究中，人们提出了多种具有平面结构的谐振器用于ESR测试，比如微带线谐振器^[6⇓-8]以及其它具有特殊形状^[9]的谐振结构，其室温灵敏度通常约为10¹⁰ spins/Gs Hz^1/2，与谐振腔的灵敏度相当；并且由于开放式的结构特点，平面谐振器能够满足对大尺寸样品进行无损测试的需求.也有研究者采用耦合微带环结构作为测试系统的谐振单元，通过在谐振器的密集微波磁场区域引入磁性材料^[10]增强磁场强度，将ESR系统的灵敏度提升到10⁸ spins/Gs Hz^1/2，相比同类型的耦合环ESR系统，其灵敏度提升了1~2个数量级.平面谐振器的设计较谐振腔结构也更加灵活，如采用“十字叉”谐振器，实现了在传统谐振腔中难于实现的微波极化方向控制，为发展量子信息技术提供了手段^[11].微带线的结构也便于采用集成电路工艺，实现对样品的微波特性与载流子输运特性（如Hall效应）的同时测量，并获得自旋动力学过程的相关参数^[12].

为获得高灵敏度，谐振器带宽通常较窄，然而窄的带宽不能适应高损耗基片的测试需求，在薄膜样品的测量应用中有一定的限制.为实现薄膜样品的ESR测试，我们选择双开口环（Double Split Ring，DSR）谐振器作为测试系统的谐振单元.该谐振器在1981年由Hardy等^[13]提出，并在超材料^[14]中得到了广泛应用.最近，DSR谐振器的近场效应也在复合介电材料的介电常数二维成像^[15]、太赫兹波段生物传感器^[16]及材料电磁特性测试^[17]中得到应用.

本文设计了工作在C波段的双口环微带谐振器，并利用该谐振器搭建了ESR测试系统，实现了对大尺寸、高介质损耗薄膜样品的无损测量.本文首先介绍了测试系统的核心部件-开路环谐振器的设计过程，并通过有限元仿真对谐振器的关键尺寸进行了优化.然后介绍了基于该谐振器的ESR系统的构成及表征.最后，通过在不同材料基底上标准样品二苯基三硝基苯肼（2, 2-diphenyl-1-picrylhydrazyl，DPPH）的测试，对大尺寸的高介质损耗薄膜材料进行了表征.

1 谐振器设计和仿真

DSR谐振器主要由阻抗匹配线和开路谐振环组成（图1），由阻抗匹配线对开路谐振环进行耦合馈电. 在谐振环的阻抗匹配线对侧放置一铜箔，通过控制铜箔到谐振环的距离可以改变谐振器的端口阻抗实现端口匹配.环形谐振器的空载谐振频率${{F}_{\text{r}}}$可由(1)式估计^[7]：

(1)${{F}_{\text{r}}}=\frac{c}{4\text{ }\!\!\pi\!\!\text{ }(r+\Delta \,r)\sqrt{{{\varepsilon }_{\text{eff}}}}}$

图1

新窗口打开| 下载原图ZIP| 生成PPT

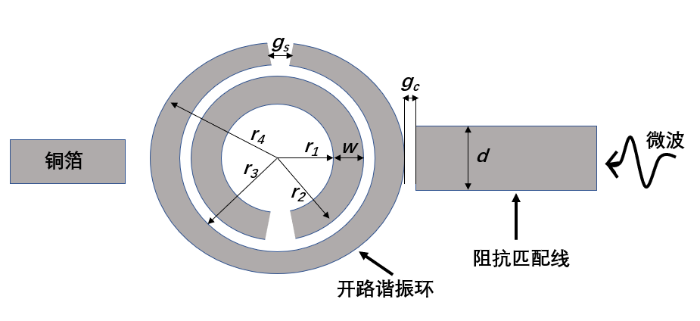
图1 双开口环（DSR）谐振器平面结构示意图.谐振环与阻抗匹配线间距为${{g}_{\text{c}}}$；谐振环宽度为w，开口间隙${{g}_{\text{s}}}=$0.5 mm，谐振环半径r₂= 3 mm、r₃= 3.2 mm、r₄= 4.2 mm；阻抗匹配线宽度d = 3.2 mm；谐振环左侧是一铜箔，通过调整铜箔位置可实现调谐

Fig. 1 Schematic of the DSR resonator. The distance between resonant ring and feeder line is${{g}_{\text{c}}}$, the width of the resonant ring is w, the gap of DSR is${{g}_{\text{s}}}=$0.5 mm, the radius values of the resonant ring are r₂= 3 mm, r₃= 3.2 mm, r₄= 4.2 mm, and the width of the feeder line is$d=$3.2 mm. Tuning is achieved by adjusting the position of the copper flake on the left side of the resonant ring

其中，c为真空中的光速，r为谐振环的半径，Δr为谐振环终端边缘电场引入的修正项，${{\varepsilon }_{\text{eff}}}$为有效介电常数.对于双环谐振器，其谐振频率主要由内环外径r₂和外环内径r₃所决定，当两者大小较为接近时（本文取内外环间隙大小为0.2 mm），内外环的谐振频率也比较接近，从而可以增加带宽、增强磁场.

通过(1)式可以估计目标频率下所需要的谐振器尺寸，但由于谐振器介电常数的不连续性及开放式的结构，难以解析获得谐振器的场分布，因此本文采用有限元分析求解器（High Frequency Structure Simulator，HFSS）对谐振器的电磁场分布进行了计算仿真.谐振器谐振频率预设定在7 GHz，本文取谐振器的半径参数为r₁ = 1.5 mm、r₂ = 3 mm、r₃ = 3.2 mm、r₄ = 4.2 mm，其中r₁ = 1.5 mm为待确定的仿真初值.为减少高频微波损耗，本文选择介电常数${{\varepsilon }_{\text{eff}}}=$3.48、损耗角正切tanδ = 0.000 9的微带线基板（RO 4350B），该基板的尺寸为40 mm×42 mm×1.6 mm.根据谐振器的端口输入阻抗为50 Ω，确定相应匹配线宽度d =3.2 mm.谐振环开口间隙的主要作用是增加耦合电容从而减小器件尺寸，本文取开口角度为20˚，此时对应的开口间隙${{g}_{\text{s}}}$约为0.5 mm.利用以上的尺寸设置，得到该谐振器的S₁₁参数、谐振频率F_r，以及品质因子${{Q}_{0}}$与关键参数（${{g}_{\text{c}}}$、w）间关系的仿真结果如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

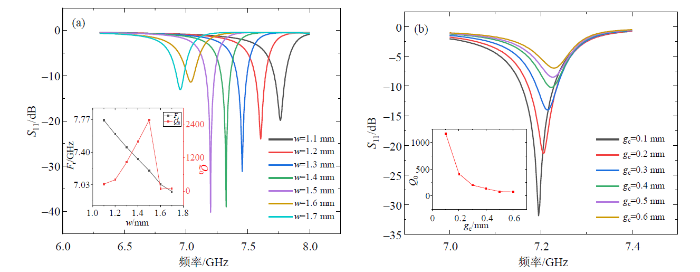
图2 (a)不同谐振环宽度w对应的S₁₁曲线仿真（${{g}_{\text{c}}}=$0.1 mm），图中插图为${{Q}_{0}}$值和谐振频率F_r随w的变化曲线.w =1.5 mm时，谐振器${{Q}_{0}}$值最大，此时F_r = 7.2 GHz；(b)不同${{g}_{\text{c}}}$值对应的S₁₁曲线仿真（w = 1.5 mm）.${{g}_{\text{c}}}=$0.1 mm时，谐振器耦合效果最好，图中插图为${{Q}_{0}}$值随${{g}_{\text{c}}}$的变化曲线

Fig. 2 (a) S₁₁ curve simulation corresponding to different w values (${{g}_{\text{c}}}=$0.1 mm), the illustration in the figure shows the influence of w on ${{Q}_{0}}$and F_r. The${{Q}_{0}}$of the resonator is the maximum and F_r is 7.2 GHz when w is 1.5 mm; (b) S₁₁ curve simulation corresponding to different ${{g}_{\text{c}}}$values (w = 1.5 mm), it would be the best coupling when${{g}_{\text{c}}}=$0.1 mm, the illustration in the figure shows the influence of${{g}_{\text{c}}}$on${{Q}_{0}}$

谐振器设计的关键优化指标是品质因子${{Q}_{0}}$，${{Q}_{0}}$值越高则表明该结构的介电损耗越小.谐振器品质因子${{Q}_{0}}$的计算公式为^[16]：

(2)${{Q}_{0}}=\frac{{{F}_{\text{r}}}}{\text{FWHM}}$

其中，FWHM为谐振器的3 dB带宽.品质因子${{Q}_{0}}$随谐振环宽度w的变化曲线如图2(a)中插图所示.从图中可以看出，当w = 1.5 mm时，${{Q}_{0}}$取最大值.

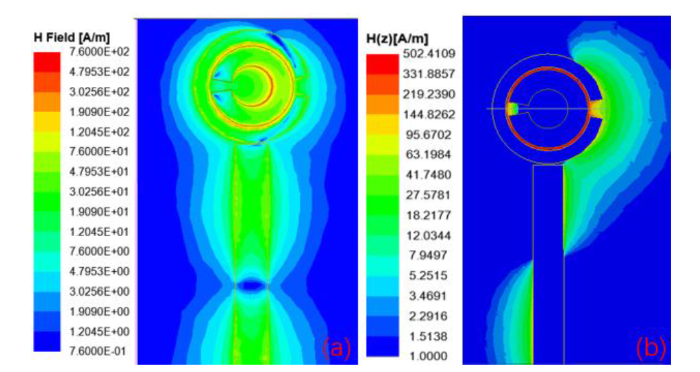
除谐振环半径和宽度w会影响谐振器的谐振频率F_r和品质因子${{Q}_{0}}$^[18]外，谐振环与馈电线的间隙${{g}_{\text{c}}}$也是影响谐振器谐振性能的关键参数.本文通过HFSS仿真得到了谐振器能量输入端口的S₁₁参数随${{g}_{\text{c}}}$的变化曲线.如图2(b)所示，在利用50 Ω阻抗匹配线馈电的情况下，${{g}_{\text{c}}}$越小则其谐振点处对应的S₁₁值越小，代表谐振器的吸收越大，谐振器的${{Q}_{0}}$值也越高，然而器件的带宽也随之减小.虽然如此，根据测试结果，当${{g}_{\text{c}}}$为0.1 mm时，微带谐振器的S₁₁在3 dB处的带宽仍然有58.7 MHz（后文图5），远大于商用ESR波谱仪谐振腔（Bruker TE₀₁₁）的3 dB带宽（1.3 MHz）.考虑到微波电路版加工精度的限制，在本谐振器中，我们选取${{g}_{\text{c}}}=$0.1 mm.根据图2(b)中黑色实线所示的S₁₁参数可知，当${{g}_{\text{c}}}=$0.1 mm、w = 1.5 mm时，该谐振器的空载谐振频率F_r = 7.2 GHz且微波吸收最强，满足设计预期，因此本文将1.5 mm和0.1 mm作为w和${{g}_{\text{c}}}$的值.

已有的研究表明谐振环的旋转角度会对谐振器的吸收谱产生一定的影响^[16]，而对ESR信号测试来说，开口位置的关键还在于其影响了谐振器的微波磁场分布.本文使两开口呈180˚取向，能够在谐振环的缝隙环形区域获得均匀沿环分布的微波磁场.在确定了谐振器的结构尺寸之后，根据HFSS的仿真结果，可以得到谐振器微波磁场分布（图3）.从图3(a)可以看到磁场主要集中在内环金属内外侧，特别是内环开口对侧.在输入端口微波功率为1 W时，谐振器表面最强磁场幅值接近760 A/m.从磁场的+z方向幅度图[图3(b)]可以看出，谐振时磁场z方向分量幅值可以达到500 A/m.从图中可以看到磁场主要分布在两环之间缝隙的区域，相比于条形微带线结构^[19]，沿缝隙分布的环状微波磁场极大地增加了磁场与薄膜材料的相互作用面积，从而增强了ESR信号.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 (a)谐振器在7.2 GHz时的磁场分布图；(b)磁场+z方向分量幅度图.+z方向的磁场均匀分布在谐振环的缝隙区域，且磁场强度达到500 A/m

Fig. 3 (a) Distribution of the magnetic field amplitude of the resonator at 7.2 GHz. (b) Distribution of the magnetic field in +z direction. The magnetic field in the +z direction is evenly distributed in the gap area of the resonant ring, and the magnetic field intensity reaches 500 A/m

2 ESR系统构成

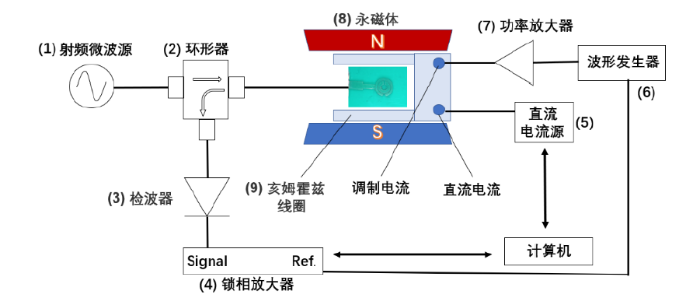
根据仿真结果，利用DSR谐振器搭建的ESR测试系统如图4所示.本系统采用永磁体和直流线圈磁场叠加的方式提供最大直流磁场H₀=3 500 Oe（1 Oe = 10^-4 T）的恒定磁场，其中直流线圈磁场通过亥姆霍兹（Helmholtz）线圈提供，变化范围为0~80 Oe.交流调制磁场通过同一线圈提供，线圈电压幅度为1 V、频率为999 Hz.由波形发生器提供频率参考信号，并通过锁相放大器SR830获得ESR信号电压.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 ESR测试系统原理图. (1)射频微波源（R&S SMB100A）；(2)环形器（DH701FD）；(3)检波器（Keysight 8471E）；(4)锁相放大器（Stanford Research SR830）；(5)直流电流源（GWINSTEK PSW）；(6)波形发生器（SIGLENT SDG1050）；(7)功率放大器（LC1901）；(8)自制永磁体；(9)自制亥姆霍兹线圈

Fig. 4 Schematic diagram of the ESR system. (1) Radiofrequency microwave source (R&S SMB100A); (2) Circulator (DH701FD); (3) Detector (Keysight 8471E); (4) Lock-in amplifier (Stanford Research SR830); (5) Direct current source (GWINSTEK PSW); (6) Waveform generator (SIGLENT SDG1050); (7) Power amplifier (LC1901); (8) Home-built permanent magnet; (9) Home-built Helmholtz coil

如前所述，本文设计的谐振器为在介质基板（RO 4350）上加工的微带线结构，其正反面实物照片如图5中插图所示.利用矢量网络分析仪（Agilent N5234A）测得的谐振器加载DPPH粉末样品及调谐前后的反射系数如图5所示，从图中可以看出由于样品的影响，谐振器的谐振频率有所改变，样品及基片使得有效介电常数增加，根据(1)式，谐振频率减小.系统的谐振频率改变后，其特性阻抗也随之变化，反射增加，但通过铜箔调谐后，其谐振点处S₁₁大小减小了3 dB，代表谐振时的微波反射是调谐前的一半，从而使得ESR信号的信噪比和系统的灵敏度得到提升.

图5

新窗口打开| 下载原图ZIP| 生成PPT

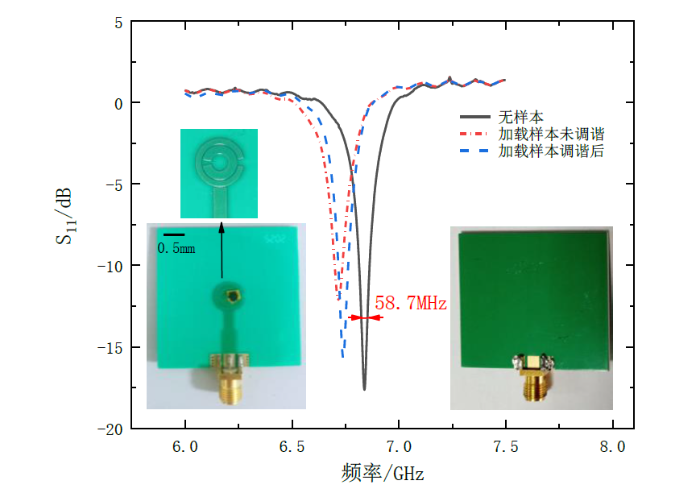
图5 利用矢量网络分析仪（Agilent N5234A）测得的谐振器空载及加载样品调谐前后的S₁₁参数曲线，图中插图为加载粉末样品的谐振器正反面的实物照片.经过铜箔调谐后，谐振点的微波反射是调谐前的一半

Fig. 5 S₁₁parameter diagram of the resonator without samples and with samples before and after tuning that is measured by vector network analyzer (VNA, Agilent N5234A); the illustration in the figure is the resonator loaded with powder sample. The microwave reflection at the resonance point is halved after tuning with copper flake

3 结果与讨论

系统灵敏度$N\min $（能探测的最少自旋数）可以通过下式计算^[7]：

(3)$N\min =\frac{1}{\text{SNR}}\frac{N\text{spin}}{\sqrt{\text{ENBW}}\cdot \Delta H}$

其中，SNR为系统的信噪比，定义为信号峰峰值与噪声均方根值之比；N_spin为样品总自旋数；ΔH为ESR信号的峰峰值带宽；ENBW为锁相放大器的等效噪声带宽，在100 ms的时间常数、24 dB/oct的衰减条件下，可得到相应的ENBW=0.78 Hz.

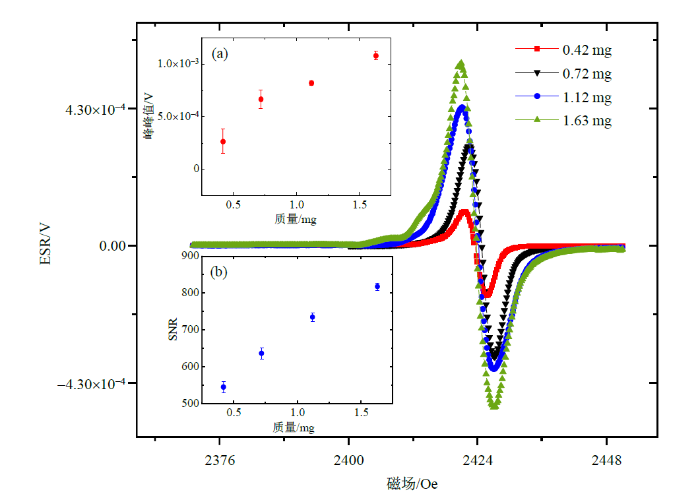
我们分别测量四个不同质量的DPPH粉末样品：m = 0.42 mg、0.72 mg、1.12 mg、1.63 mg.根据DPPH的密度约为1.2 g/cm³、自旋密度2×10²⁷ m^-3，得到其单位质量的自旋密度为1.67×10¹⁸ mg^-1.为了兼顾实验的稳定性和准确性，实验中直流磁场扫描步长设置为0.2 Oe，微波频率设置为6.82 GHz，功率为17 dbm，磁场调制频率999 Hz，常温下测得的ESR信号如图6所示.四个样品的ESR信号峰峰值ΔH及信噪比SNR如图6中的插图(a)和(b)所示.通过四个样品的测试结果，可以估计本系统在室温时的灵敏度约为4.39×10¹⁴ spins/Gs Hz^1/2.该数值略低于文献^[19]中的灵敏度3.3×10¹² spins/Gs Hz^1/2，主要原因是有效磁场区域仅分布于两环间约0.2 mm宽度的间隙范围内，在计算自旋数目时无法准确计入有效的自旋数.采用有效面积估计后，探测灵敏度约为9.66×10¹² spins/Gs Hz^1/2，与其它微带线谐振器的报道结果相当^[19].

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 室温下，四个不同质量（m = 0.42、0.72、1.12及1.63 mg）的DPPH粉末样品获得的ESR信号，图中插图为四个ESR信号的峰峰值(a)和信噪比(b).相关测试参数为：微波功率 = 17 dBm，微波频率f = 6.82 GHz，磁场调制频率为999 Hz，锁放时间常数为100 ms，衰减为24 dB/oct，ENBW = 0.78 Hz

Fig. 6 ESR signal of DPPH powder of different quality (m = 0.42, 0.72, 1.12 and 1.63 mg) at room temperature. The peak-to-peak values (a) and SNR (b) of the four ESR signals are illustrated in the figure. Experimental parameters: microwave power =17 dBm, microwave frequency f = 6.82 GHz, magnetic field modulation frequency = 999 Hz, lock-in time constant = 100 ms, roll-off = 24 dB/oct, ENBW = 0.78 Hz

如前文所述，样品基底的介电常数及介电损耗，将影响谐振器的响应特性，特别是谐振频率将发生改变.对于本文搭建的系统，即使谐振频率改变，也不影响对样品的ESR测试.本文分别使用微晶玻璃Zerodur和硅（Si）片作为基底材料，其中微晶玻璃${{\varepsilon }_{\text{eff}}}=$6.71、tanδ = 0.05；硅${{\varepsilon }_{\text{eff}}}=$11.50、tanδ = 0.10.从S₁₁参数曲线可以看出（图7），在相同的DPPH样品上覆盖以上两种基底材料时，仅仅是谐振频率发生了偏移，其谐振峰频率F_r分别变为6.57 GHz和6.35 GHz.分别在这两个频率点附近（f = 6.55 GHz和6.22 GHz）进行ESR测试，测试结果如图7中插图(a)和(b)所示.朗德g因子是表征原子磁矩和角动量关系的无量纲物理量，根据图7的测试结果，由公式$\hbar f=g\beta {{H}_{r}}$（$\hbar $为普朗克常数，$\beta $为玻尔磁子，${{H}_{r}}$为谐振时的直流磁场）可以得到两种基底上的DPPH标样的g值分别为1.972 3和1.973 1，相对误差约0.041%.从测试的结果可以看到，基于平面双环谐振器的ESR测试系统能够对多种基底的薄膜材料进行表征，不同介电常数的基底将导致不同的谐振频率.不同样品的测试结果的误差主要来源于由系统装样位置偏移导致的磁场误差.

图7

新窗口打开| 下载原图ZIP| 生成PPT

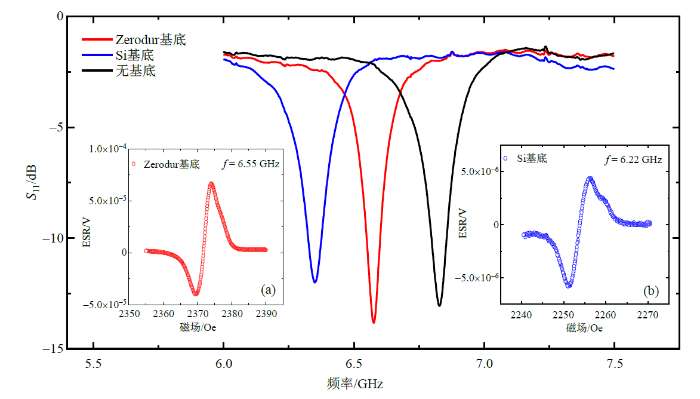
图7 两种不同基底材料及无基底时谐振器的S₁₁曲线，图中插图(a)为Zerodur作基底时DPPH样品的ESR信号，插图(b)为Si作基底时样品的ESR信号.当谐振器加载Zerodur和Si时，谐振器谐振频率分别偏移到6.57 GHz和6.35 GHz.两次测试得到的g值分别为1.972 3和1.973 1，相对误差为0.041%

Fig. 7 (a) S₁₁ curves of the resonator with two different substrate materials and without substrate, illustration (a) shows the measured ESR signal of DPPH covered with Zerodur, illustration (b) shows the measured ESR signal of DPPH covered with Si. The resonant frequency of the resonator changes to 6.57 GHz and 6.35 GHz while Zerodur and Si are loaded. The g values obtained from the two side tests are 1.972 3 and 1.973 1, respectively, with a relative error of 0.041%

4 结论

本文设计了基于双开口谐振环的微带线谐振器，并利用其实现了薄膜材料的ESR谱的非破坏性表征.通过对毫克级DPPH标样粉末的测试，获得该系统的室温灵敏度约为10¹³ spins/Gs Hz^1/2.对以硅片和微晶玻璃为基底旋涂的DPPH样品的测试结果表明，本系统不受基片大小及介电损耗的影响，能够获得大尺寸、高损耗薄膜样品的ESR信号.同时，本文采用永磁体配合小功率可变电源提供磁场，结合平面化的谐振结构，易于实现便携式的ESR测试平台.谐振器开放式的平面结构也为材料物性与微波场的耦合研究提供了便利，从而可实现多物理效应的耦合表征.

利益冲突

无

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

SHIN

C S

, DUNNAM

C R

, BORBAT

P P

, et al.

ESR microscopy for biological and biomedical applications

[J]. Nanosci Nanotechnol Lett, 2011, 3: 561-567.

DOI:10.1166/nnl.2011.1206 URL [本文引用: 1]

[2]

SCHWEIGER

, JESCHKE

. Principles of pulse electron paramagnetic resonance[M]. Oxford University Press on Demand, 2001.

[本文引用: 1]

[3]

YOSHIMURA

, YOKOYAMA

, FUJII

, et al.

In vivo EPR detection and imaging of endogenous nitric oxide in lipopolysaccharide-treated mice

[J]. Nat Biotech, 1996, 14(8): 992-994.

DOI:10.1038/nbt0896-992 URL [本文引用: 1]

[4]

SIGILLITO

A J

, MALISSA

, TYRYSHKIN

A M

, et al.

Fast, low-power manipulation of spin ensembles in superconducting microresonators

[J]. Appl Phys Lett, 2014, 104(22): 222407.

DOI:10.1063/1.4881613 URL [本文引用: 1]

[5]

LYNCH

W B

, EARLE

K A

, FREED

J H

1‐mm wave ESR spectrometer

[J]. Rev Sci Instrum, 1988, 59(8): 1345-1351.

DOI:10.1063/1.1139720 URL [本文引用: 1]

[6]

ROY

, SAHA

, SARKAR

, et al.

Development of planar microstrip resonators for electron spin resonance spectroscopy

[J]. Eur Phys J-Appl Phys, 2020, 90(3): 31001.

DOI:10.1051/epjap/2020200108 URL [本文引用: 1]

[7]

TORREZAN

A C

, MAYER

ALEGRE T P

, MEDEIROS-RIBEIRO

Microstrip resonators for electron paramagnetic resonance experiments

[J]. Rev Sci Instrum, 2009, 80(7): 075111.

DOI:10.1063/1.3186054 URL [本文引用: 3]

[8]

WALLACE

W J

, SILSBEE

R H

Microstrip resonators for electron‐spin resonance

[J]. Rev Sci Instrum, 1991, 62(7): 1754-1766.

DOI:10.1063/1.1142418 URL [本文引用: 1]

[9]

NARKOWICZ

, SUTER

, STONIES

Planar microresonators for EPR experiments

[J]. J Magn Reson, 2005, 175(2): 275-284.

PMID:15939642 [本文引用: 1]

EPR resonators on the basis of standing-wave cavities are optimised for large samples. For small samples it is possible to design different resonators that have much better power handling properties and higher sensitivity. Other parameters being equal, the sensitivity of the resonator can be increased by minimising its size and thus increasing the filling factor. Like in NMR, it is possible to use lumped elements; coils can confine the microwave field to volumes that are much smaller than the wavelength. We discuss the design and evaluation of EPR resonators on the basis of planar microcoils. Our test resonators, which operate at a frequency of 14 GHz, have excellent microwave efficiency factors, achieving 24 ns pi/2 EPR pulses with an input power of 17 mW. The sensitivity tests with DPPH samples resulted in the sensitivity value 2.3 x 10(9) spins.G(-1) Hz(-1/2) at 300 K.

[10]

HOLE

A P

, PULIJALA

A miniaturized on-chip electron paramagnetic resonance sensor

[J]. IEEE T Electron Dev, 2021, 68(12): 6407-6414.

DOI:10.1109/TED.2021.3117899 URL [本文引用: 1]

[11]

HENDERSON

J J

, RAMSEY

C M

, QUDDUSI

H M

, et al.

High-frequency microstrip cross resonators for circular polarization electron paramagnetic resonance spectroscopy

[J]. Rev Sci Instrum, 2008, 79(7): 074704.

DOI:10.1063/1.2957621 URL [本文引用: 1]

[12]

QUDDUSI

H M

, RAMSEY

C M

, GONZALEZ-PONS

J C

, et al.

On-chip integration of high-frequency electron paramagnetic resonance spectroscopy and Hall-effect magnetometry

[J]. Rev Sci Instrum, 2008, 79(7): 074703.

DOI:10.1063/1.2957616 URL [本文引用: 1]

[13]

HARDY

W N

, WHITEHEAD

L A

Split‐ring resonator for use in magnetic resonance from 200-2000 MHz

[J]. Rev Sci Instrum, 1981, 52(2): 213-216.

DOI:10.1063/1.1136574 URL [本文引用: 1]

[14]

WANG

J F

, QU

S B

, XU

, et al.

A controllable magnetic metamaterial: split-ring resonator with rotated inner ring

[J]. IEEE T Antenn Propag, 2008, 56(7): 2018-2022.

DOI:10.1109/TAP.2008.924728 URL [本文引用: 1]

[15]

ISAKOV

, STEVENS

C J

, CASTLES

, et al.

A split ring resonator dielectric probe for near-field dielectric imaging

[J]. Sci Rep, 2017, 7(1): 1-9.

DOI:10.1038/s41598-016-0028-x URL [本文引用: 1]

[16]

H Y

, LI

, JIANG

Y Y

, et al.

Double-opening metal ring based terahertz metamaterial absorber sensor

[J]. Acta Physica Sinica, 2022, 71(10): 108701.

DOI:10.7498/aps.71.20212303 URL [本文引用: 3]

葛宏义, 李丽, 蒋玉英, 等.

基于双开口金属环的太赫兹超材料吸波体传感器

[J]. 物理学报, 2022, 71(10): 108701.

DOI:10.7498/aps.71.20212303 URL [本文引用: 3]

[17]

BOBOWSKI

J S

Using split-ring resonators to measure the electromagnetic properties of materials: An experiment for senior physics undergraduates

[J]. Am J Phys, 2013, 81(12): 899-906.

DOI:10.1119/1.4823807 URL [本文引用: 1]

[18]

PENDRY

J B

, HOLDEN

A J

, ROBBINS

D J

, et al.

Magnetism from conductors and enhanced nonlinear phenomena

[J]. IEEE T Micro Theory, 1999, 47(11): 2075-2084.

DOI:10.1109/22.798002 URL [本文引用: 1]

[19]

JING

, LAN

Z H

, SHI

Z F

, et al.

Broadband electron paramagnetic resonance spectrometer from 1 to 15 GHz using metallic coplanar waveguide

[J]. Rev Sci Instrum, 2019, 90(12): 125109.

DOI:10.1063/1.5119333 URL [本文引用: 3]

ESR microscopy for biological and biomedical applications

2011

... 电子自旋共振（Electron Spin Resonance，ESR），又称电子顺磁共振（Electron Paramagnetic Resonance，EPR），是指当处于直流磁场中的未成对电子受到微波磁场作用，电子自旋的Larmor进动频率与激励的微波频率相等时，产生共振吸收的现象.ESR在生物、物理以及材料科学中有重要的应用^[1⇓⇓-4].在通常的ESR测试中，常采用X波段（8~12 GHz）金属谐振腔^[5]作为谐振单元，利用谐振腔在TE₀₁₁模式下产生的轴向微波磁场激励样品以获得ESR信号，其室温灵敏度（可探测到的最小自旋数）可以超过10¹¹ spins/Gs Hz^1/2（1 Gs = 10^-4 T）.然而受谐振腔腔体体积的限制，在ESR测试中，需要将样品尺寸限制在1 mm³以内以放入石英管中，这极大地限制了ESR在材料表征中的应用：比如不能同时对同一薄膜的自旋以及输运特性等其它特性进行表征；或者样品破坏后也可能无法根据ESR结果对同一样品进行进一步表征.在近年的研究中，人们提出了多种具有平面结构的谐振器用于ESR测试，比如微带线谐振器^[6⇓-8]以及其它具有特殊形状^[9]的谐振结构，其室温灵敏度通常约为10¹⁰ spins/Gs Hz^1/2，与谐振腔的灵敏度相当；并且由于开放式的结构特点，平面谐振器能够满足对大尺寸样品进行无损测试的需求.也有研究者采用耦合微带环结构作为测试系统的谐振单元，通过在谐振器的密集微波磁场区域引入磁性材料^[10]增强磁场强度，将ESR系统的灵敏度提升到10⁸ spins/Gs Hz^1/2，相比同类型的耦合环ESR系统，其灵敏度提升了1~2个数量级.平面谐振器的设计较谐振腔结构也更加灵活，如采用“十字叉”谐振器，实现了在传统谐振腔中难于实现的微波极化方向控制，为发展量子信息技术提供了手段^[11].微带线的结构也便于采用集成电路工艺，实现对样品的微波特性与载流子输运特性（如Hall效应）的同时测量，并获得自旋动力学过程的相关参数^[12]. ...

2001

In vivo EPR detection and imaging of endogenous nitric oxide in lipopolysaccharide-treated mice

1996

Fast, low-power manipulation of spin ensembles in superconducting microresonators

2014

1‐mm wave ESR spectrometer

1988

Development of planar microstrip resonators for electron spin resonance spectroscopy

2020

Microstrip resonators for electron paramagnetic resonance experiments

2009

... DSR谐振器主要由阻抗匹配线和开路谐振环组成（图1），由阻抗匹配线对开路谐振环进行耦合馈电. 在谐振环的阻抗匹配线对侧放置一铜箔，通过控制铜箔到谐振环的距离可以改变谐振器的端口阻抗实现端口匹配.环形谐振器的空载谐振频率

${{F}_{\text{r}}}$

可由(1)式估计^[7]： ...

... 系统灵敏度

$N\min $

（能探测的最少自旋数）可以通过下式计算^[7]： ...

Microstrip resonators for electron‐spin resonance

1991

Planar microresonators for EPR experiments

2005

A miniaturized on-chip electron paramagnetic resonance sensor

2021

High-frequency microstrip cross resonators for circular polarization electron paramagnetic resonance spectroscopy

2008

On-chip integration of high-frequency electron paramagnetic resonance spectroscopy and Hall-effect magnetometry

2008

Split‐ring resonator for use in magnetic resonance from 200-2000 MHz

1981

... 为获得高灵敏度，谐振器带宽通常较窄，然而窄的带宽不能适应高损耗基片的测试需求，在薄膜样品的测量应用中有一定的限制.为实现薄膜样品的ESR测试，我们选择双开口环（Double Split Ring，DSR）谐振器作为测试系统的谐振单元.该谐振器在1981年由Hardy等^[13]提出，并在超材料^[14]中得到了广泛应用.最近，DSR谐振器的近场效应也在复合介电材料的介电常数二维成像^[15]、太赫兹波段生物传感器^[16]及材料电磁特性测试^[17]中得到应用. ...

A controllable magnetic metamaterial: split-ring resonator with rotated inner ring

2008

A split ring resonator dielectric probe for near-field dielectric imaging

2017

基于双开口金属环的太赫兹超材料吸波体传感器

2022

... 谐振器设计的关键优化指标是品质因子

${{Q}_{0}}$

，

${{Q}_{0}}$

值越高则表明该结构的介电损耗越小.谐振器品质因子

${{Q}_{0}}$

的计算公式为^[16]： ...

... 已有的研究表明谐振环的旋转角度会对谐振器的吸收谱产生一定的影响^[16]，而对ESR信号测试来说，开口位置的关键还在于其影响了谐振器的微波磁场分布.本文使两开口呈180˚取向，能够在谐振环的缝隙环形区域获得均匀沿环分布的微波磁场.在确定了谐振器的结构尺寸之后，根据HFSS的仿真结果，可以得到谐振器微波磁场分布（图3）.从图3(a)可以看到磁场主要集中在内环金属内外侧，特别是内环开口对侧.在输入端口微波功率为1 W时，谐振器表面最强磁场幅值接近760 A/m.从磁场的+z方向幅度图[图3(b)]可以看出，谐振时磁场z方向分量幅值可以达到500 A/m.从图中可以看到磁场主要分布在两环之间缝隙的区域，相比于条形微带线结构^[19]，沿缝隙分布的环状微波磁场极大地增加了磁场与薄膜材料的相互作用面积，从而增强了ESR信号. ...

基于双开口金属环的太赫兹超材料吸波体传感器

2022

... 谐振器设计的关键优化指标是品质因子

${{Q}_{0}}$

，

${{Q}_{0}}$

值越高则表明该结构的介电损耗越小.谐振器品质因子

${{Q}_{0}}$

的计算公式为^[16]： ...

Using split-ring resonators to measure the electromagnetic properties of materials: An experiment for senior physics undergraduates

2013

Magnetism from conductors and enhanced nonlinear phenomena

1999

... 除谐振环半径和宽度w会影响谐振器的谐振频率F_r和品质因子

${{Q}_{0}}$

^[18]外，谐振环与馈电线的间隙

${{g}_{\text{c}}}$

也是影响谐振器谐振性能的关键参数.本文通过HFSS仿真得到了谐振器能量输入端口的S₁₁参数随

${{g}_{\text{c}}}$

的变化曲线.如图2(b)所示，在利用50 Ω阻抗匹配线馈电的情况下，

${{g}_{\text{c}}}$

越小则其谐振点处对应的S₁₁值越小，代表谐振器的吸收越大，谐振器的

${{Q}_{0}}$

值也越高，然而器件的带宽也随之减小.虽然如此，根据测试结果，当

${{g}_{\text{c}}}$

为0.1 mm时，微带谐振器的S₁₁在3 dB处的带宽仍然有58.7 MHz（后文图5），远大于商用ESR波谱仪谐振腔（Bruker TE₀₁₁）的3 dB带宽（1.3 MHz）.考虑到微波电路版加工精度的限制，在本谐振器中，我们选取

${{g}_{\text{c}}}=$

0.1 mm.根据图2(b)中黑色实线所示的S₁₁参数可知，当

${{g}_{\text{c}}}=$

0.1 mm、w = 1.5 mm时，该谐振器的空载谐振频率F_r = 7.2 GHz且微波吸收最强，满足设计预期，因此本文将1.5 mm和0.1 mm作为w和

${{g}_{\text{c}}}$

的值. ...

Broadband electron paramagnetic resonance spectrometer from 1 to 15 GHz using metallic coplanar waveguide

2019

... 我们分别测量四个不同质量的DPPH粉末样品：m = 0.42 mg、0.72 mg、1.12 mg、1.63 mg.根据DPPH的密度约为1.2 g/cm³、自旋密度2×10²⁷ m^-3，得到其单位质量的自旋密度为1.67×10¹⁸ mg^-1.为了兼顾实验的稳定性和准确性，实验中直流磁场扫描步长设置为0.2 Oe，微波频率设置为6.82 GHz，功率为17 dbm，磁场调制频率999 Hz，常温下测得的ESR信号如图6所示.四个样品的ESR信号峰峰值ΔH及信噪比SNR如图6中的插图(a)和(b)所示.通过四个样品的测试结果，可以估计本系统在室温时的灵敏度约为4.39×10¹⁴ spins/Gs Hz^1/2.该数值略低于文献^[19]中的灵敏度3.3×10¹² spins/Gs Hz^1/2，主要原因是有效磁场区域仅分布于两环间约0.2 mm宽度的间隙范围内，在计算自旋数目时无法准确计入有效的自旋数.采用有效面积估计后，探测灵敏度约为9.66×10¹² spins/Gs Hz^1/2，与其它微带线谐振器的报道结果相当^[19]. ...

... [19]. ...

〈

〉