引言
水分子的扩散系数会随局部环境的变化而变化,因此扩散张量可以作为组织结构的探针.DTI技术可用于研究健康被试和脑疾病患者之间脑白质的各向异性(Fractional Anisotropy,FA)差异,以及健康被试性别与年龄之间的差异[4],目前已被癫痫[5]、精神分裂症[6]、躁郁症[7]、脑中风[8]、老年痴呆[9]和创伤性脑损伤[10]等脑疾病研究采用.现阶段主要有两种方法用以比较被试组间FA的差异:1)感兴趣区域(Region of Interest,ROI)分析法,该方法在图像中手动或半自动选取ROI,然后比较被试ROI内平均FA的差异[11],但由于被试大脑各脑区的位置稍有不同,因此ROI分析无法比较主要扩散方向等特征;2)基于体素分析法(Voxel-Based Analysis,VBA),对生成的DTI平均数据(此处的平均是指获取数据之前对同一被试多次测量取平均值)进行分析,比较选定ROI内的数据,或者进行逐一体素分析[12, 13].然而,VBA依赖于数据集的联合配准[14, 15],具体是将每个被试的样本数据都配准到DTI模板上进行空间标准化,然后在组间进行定量统计分析.除用于VBA外,由于各个被试的大脑数据并不会完全对齐,空间标准化能够将所有被试的数据统一到同一个空间坐标中以便后续的处理分析,因此空间标准化也常作为DTI数据的预处理步骤之一[16].DTI数据的空间标准化通常需要借助对应的结构图像,可先将对应的T1加权或T2加权图像配准到MNI(Montreal Neurological Institute)[17]空间以得到变形场T,再将T作用于原图像以达到DTI空间标准化的目的.或者选择一个被试的DTI数据作为参考图像,然后将其他被试的DTI数据配准到参考图像.但单个被试的大脑图像特征无法代表整个被试群体,且相比于将多个被试大脑图像进行平均生成的模板,单个被试的大脑数据包含较大噪声,会降低空间标准化的准确性.因此,构建一个具有代表性的DTI人脑模板[18]对于准确比较群组大脑结构的完整性和连通性至关重要.
DTI脑模板的构建方法受被试的数量和年龄、主磁场的强度、扫描序列以及空间标准化的影响:1)如果用于构建脑模板的被试样本量较少,构建的脑模板不具备普遍性,则无法作为通用模板;2)如果主磁场强度较低,会导致图像的信噪比较低,进而影响整个模板的分辨率;3)用平面回波成像(Echo Planar Imaging,EPI)序列图像构建的脑模板会受到伪影的影响;4)使用仿射变换等线性变换进行配准,对于复杂且形状各异的解剖结构的形变形式仍为直线映射到直线,因此会在计算图片相似性时造成误差,使得具有复杂形状解剖的结构在配准后无法保持原有的形状;5)FA模板这类标量模板缺少张量的方向信息,不能保证主体被试之间的扩散特性是匹配的.不少研究者基于此对脑模板构建流程进行了优化.Jones等[19]将11名被试的DTI数据配准到对应的T2数据上以得到T2空间的DTI数据,随后将其中10名T2空间的DTI数据与T2模板进行配准,将配准得到的变形场应用于第11位被试的FA图从而得到FA模板.相比EPI序列,线扫描对运动及磁敏性伪影不敏感,且具有较高的空间分辨率.为了弥补EPI序列获取的图像用于DTI脑模板研究时的缺陷,Park等[20]选取了线扫描序列采集的图像,基于多通道非线性配准算法构建模板.此后,Zhang等[21]将一个被试的DTI数据配准到MNI空间,构建了DTI脑模板.Muller等[22]将被试的b0图像配准到ICBM-152(International Consortium of Brain Mapping-152)模板,随后通过自动注册工具箱(Automatic Registration Toolbox,ART)进行高维配准,最后将ICBM空间的被试张量数据进行平均得到模板张量.Mori等[23]通过将81个被试的DTI数据配准到ICBM空间完成初步空间标准化,随后从初步空间标准化后的DTI数据中提取张量,并通过线性平均得到脑模板的张量.Peng等[24]将被试的b0图像配准到ICBM-152模板,将距离ICBM-152模板最近的b0图像定义为初始模板,之后将剩余被试的DTI分别进行平均得到每个被试对应的平均DTI,平均DTI与初始模板进行配准得到对应的变形场,将每个被试的DTI通过变形场映射到模板空间并计算张量,最后对张量进行线性平均得到最终模板IIT.之后,Zhang等[25]对IIT模板进行了优化,使用高维配准替代了IIT构建中的低维配准,从而构建了更清晰的IIT2模板.为了得到更高质量的图像,Varentsova等[26]通过低角度分辨率的多镜头扩散数据生成高角度分辨率的扩散图像模板以提高模板清晰度.除了构建DTI张量模板,Jahanshad等[27]通过分析来自不同地点的人脑数据构建了FA标量模板.
尽管目前用于脑模板构建的算法已经比较成熟.但以往的算法都是基于配准算法或者图像本身质量的改进.这些算法针对图像清晰度进行了优化,最终也得到了比优化前更加清晰的模板图像.然而,在张量平均这一步骤中直接对张量进行线性平均会忽略张量中的向量信息;且线性平均会使灰质和白质交界处过于平滑,降低分辨率.
针对以上问题,本文在构建DTI脑模板的“将张量进行几何平均”这一步骤中引入四元数及高斯加权,从而构建了一种高斯DTI模板.为了对比该模板,本文还采用线性加权构建线性DTI脑模板.
1 实验部分
1.1 数据获取
数据来自55位国内健康志愿者,年龄范围为19~30岁.DTI数据使用12通道标准头部线圈、Siemens Trio Tim 3.0T MRI扫描仪和EPI序列采集获得,参数设置如下:回波时间(Echo Time,TE)为89 ms,重复时间(Repetition Time,TR)为8 000 ms,层数为62,层厚为2.2 mm,层间距为0 mm,层相位编码方向为前联合到后联合,扫描视野(Field of View,FOV)为282×282 mm2,采集矩阵为128×128,每层采集30个梯度方向(b=1 000 s/mm2).本文实验数据从北京师范大学(Beijing Normal University,BNU)基于连接的脑成像研究数据库下载,该数据的下载地址为http://dx.doi.org/10.15387/fcp_indi.corr.bnu1.
1.2 实验方法
常规脑模板构建算法的流程中,在计算得到多个被试的张量数据后通常将其进行多通道线性平均以得到模板的张量,这一步骤忽略了张量中的向量信息.同时,“线性平均”这一处理也易受差异较大的样本的影响.为此,本文构建了一种高斯DTI模板,引入了四元数及高斯加权平均以优化常规脑模板构建算法.
首先对55个被试的DTI数据进行预处理,使得数据伪影最小化;通过欧氏距离选出最接近整体的一个被试DTI数据作为初始模板;然后采用基于扩散张量成像工具包(Diffusion Tensor Imaging ToolKit,DTI-TK)的扩散张量图像形变配准方法将其他被试配准到初始模板上以完成初步空间标准化,其中张量重定向使用的是有限应变(Finite Strain,FS)校正;之后计算出初步空间标准化后被试DTI的张量;最后将每个体素的张量通过特征分解得到代表张量方向的特征向量和代表张量分量大小的特征值.分别将特征向量转化为四元数进行高斯加权平均得到平均后的特征向量,同时对特征值进行高斯加权平均得到平均后的特征值,以平均后的特征向量和平均后的特征值重建得到高斯张量模板;将高斯张量模板与线性平均后的b0图像重建为高斯DTI模板.
同时分别将特征向量转化为四元数进行线性平均后还原为特征向量,将该特征向量与线性平均后的特征值重建生成线性张量模板,将线性张量模板与线性平均后的b0图像重建为线性DTI模板.以此作为对照组来验证高斯加权的引入对脑模板构建的影响.随后,本文将55个被试的张量直接进行线性平均,构建了无四元数引入的线性张量模板,以此验证四元数的引入对脑模板构建的影响.
该实验所用到的软件包括MATLAB 2016a、FMRIB Software Library(FSL)、DTI-TK.涡流校正、运动校正及脑实质提取均在LINUX 2018中进行,其余实验在Windows 10中进行.该实验各步骤均通过8核i7-7700 CPU@3.60GHz处理器运行.
1.2.1 预处理
DTI图像采集过程中,梯度线圈产生的非线性变化的磁场梯度会诱发MRI扫描仪的导电结构产生涡流,从而生成额外的磁场,使得获取的实际磁场梯度不同于设定值,导致实际的b矩阵与设定之间存在差异[28].另外,图像读取过程中质子的磁化强度矢量的缓慢衰减会导致DTI图像的几何失真,如果未对失真图像进行补偿,那么基于该图像估计的扩散参数会出现明显的系统误差,从而影响后续研究的准确性.
基于EPI序列采集的DTI图像容易受到涡流伪影的影响,为减少涡流引起的图像畸变以及由被试运动导致的DTI图像伪影,本文首先通过FSL软件包的eddy_correct工具箱对DTI数据进行涡流校正和运动校正,选取b0图像为参考图像,对30个方向的EPI图像进行仿射线性变换.然后采用脑实质提取(Brain Extraction Tool,BET)算法对完成涡流及运动校正的图像进行去脑壳处理,同时获取对应的掩模图像.
1.2.2 空间标准化
分别计算每幅图像与其他图像之间的欧氏距离并计算均值,采用距离最小的图像(第42个样本,距离最小为0.631 5)作为初始模板.之后将其他DTI图像配准到初始模板上.DTI图像配准的目的是得到图像
对于标量图像,图像变换仅改变每个点x的位置,即
DTI-TK的独特之处在于将张量重定向纳入显式定向优化的解析目标函数中,通过仿射变换的雅克比矩阵极分解参数化后,结合FS策略进行重定向,使得每个张量达到最佳重定向来优化配准.
雅克比矩阵极分解将非奇异矩阵M分解为正交矩阵Q(纯旋转)和对称正定矩阵S(纯变形),使得M=QS.由于M表示某种物理变换的雅可比矩阵,因此具有一个正行列式,所以Q保证是一个旋转矩阵.该算法依赖于此分解的两个重要性质:(1)M与其分解之间的关系是双向映射的,因此可以根据M的极分解唯一地参数化M;(2)纯旋转Q是M的最佳正交逼近,因此,Q是解决FS重新定向策略的精确解.
FS策略的具体步骤如下:(1)将仿射变换M分解为M=QS,其中Q是一个正交矩阵,表示仿射变换M的旋转部分,S是一个上三角矩阵,表示仿射变换M的变形部分;(2)根据公式D'=QTDQ获得重定向后的张量D',只将变换的旋转部分Q作用于张量D,形变部分S对张量并没有影响.
在DTI-TK的方法框架内,相比于保留主方向(Preservation of Principle Direction,PPD)重定向,FS重定向有两个优点:(1)FS重定向中的旋转是以M为单位进行分析的,而PPD旋转是算法性的,没有闭合形式的表达式;(2)通过仿射参数化自动确定FS重定向,而PPD重定向需要特征分解,因此FS计算成本更低.
1.2.3 多被试张量平均
对初步空间标准化后的张量进行特征分解得到特征向量及特征值,将特征向量转换为四元数后,分别对四元数和特征值进行线性平均后生成线性张量模板,对四元数和特征值进行高斯平均后生成高斯张量模板.随后结合张量模板与b0均值图像生成对应的DTI模板.高斯平均步骤如下:
(1)随机生成1×55的一维高斯系数
其中
(2)计算每个DTI数据
(3)对计算得到的55个总距离降序排列,并求出排序后每个总距离对应的被试索引坐标;
(4)对高斯系数进行升序排列;
(5)将步骤(3)中的索引与步骤(4)中的高斯系数进行对应,并根据如下公式进行对数欧几里德高斯加权处理,获取每个体素位置的3个最终特征值.
其中,
1.3 脑模板参数评估
我们通过以下6种评估参数定量比较了高斯DTI模板和线性DTI模板对人脑细节的保留程度.将配准至初始模板的数据分别通过高斯DTI模板和线性DTI模板进行空间标准化,计算标准化前后数据之间的评估参数.空间标准化前后数据的匹配程度越低,表明配准到该模板后图像的形变越大,即该模板没有很好的保留原始数据的细节.
(1)两个张量
该指标评估了两个张量之间的距离,其值越大表明两个张量距离越远.
(2)两个偏张量(
其中,D表示扩散张量,I为单位矩阵.DVED指标评估了两个偏张量之间的距离,其值越大表明两个偏张量距离越远.
(3)估计张量中特征值(λ)与特征向量(ε)对之间的重叠部分:
其中
(4)两个张量图像主特征向量之间的一致性由COH指标评估,该值越大表明两个向量越一致:
其中,
其中,
(5)两个FA图之间的关联程度由
其中
(6)特征向量之间的夹角计算:
其中,
2 结果与讨论
2.1 实验结果可视化
图1
图1
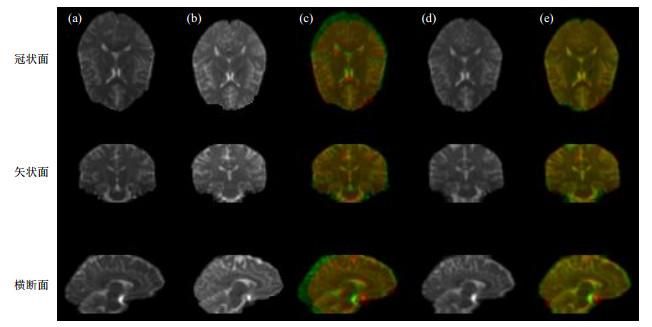
一例被试的扩散加权图像与初始模板配准前后的变化.(a)配准前,被试的扩散加权图像;(b)初始模板;(c)配准前,被试(绿色图层)与初始模板(红色图层)的叠加图;(d)配准后,被试的扩散加权图像;(e)配准后,被试(绿色图层)与初始模板(红色图层)的叠加图
Fig.1
Changes in a subject's diffusion-weighted images before and after registration to the initial template. (a) Diffusion-weighted image of the subject before registration; (b) The initial template; (c) Overlay of the subject (green layer) before registration and the initial template (red layer); (d) The diffusion-weighted images of the subject after registration; (e) Overlay of the subject (green layer) after registration and the initial template (red layer)
图 2所示为构建张量模板的平均特征向量及平均特征值.其中图 2(a)和图 2(c)中九个小图分别表示了高斯模板和线性模板中特征向量的9个分量;图 2(b)和图 2(d)中三个小图分别表示了特征值的3个通道.对比图 2(a)和图 2(c)可知特征向量中存在的较强向量噪声使得两个模板的特征向量没有出现较大差异.而图 2(b)的白质区域的强度相较图 2(d)稍高,表明相较于线性模板,高斯模板在分辨率上更有优势.图 3显示了高斯DTI模板和线性DTI模板的FA图之间的一致性.为了使图像背景统一为黑色,对图 3(a)做了255-xi的处理,因此图中黑色部分表明两个模板一致性高,白色部分表明两模板一致性低.由图 3(a)可知两个模板在海马等白质区域一致性较低,而在灰质区域一致性较高.上述结果表明高斯DTI模板和线性DTI模板在灰质和白质边界处有较大差异.
图2
图2
(a) 高斯模板的特征向量;(b)高斯模板的特征值;(c)线性模板的特征向量;(d)线性模板的特征值
Fig.2
(a) The eigenvectors of Gaussian template; (b) The eigenvalues of Gaussian template; (c) The eigenvectors of linear template; (d) The eigenvalues of linear template
图3
图3
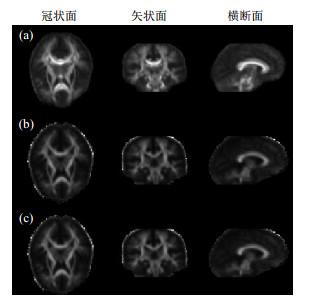
(a) 高斯DTI模板与线性DTI模板的FA图的一致性.(b)高斯DTI模板的FA图,用来对应(a)图中的位置;(c)线性DTI模板的FA图,用来对应(a)图中的位置
Fig.3
(a) Correlation consistency between FA map of Gaussian DTI template and that of linear DTI template. (b) FA map of Gaussian DTI template, used to correspond to the position in Fig. (a); (c) FA map of linear DTI template, used to correspond to the position in Fig. (a)
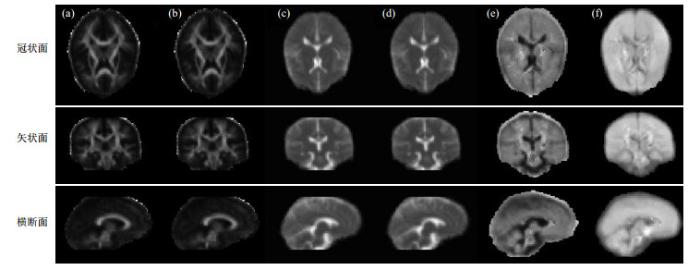
作为临床广泛使用的两个重要参数,FA反映测量不同方向的水迁移率的变异性,平均弥散度(Mean Diffusivity,MD)测量与方向无关的平均扩散率.由大脑DTI数据获得的FA和MD图通常用于定位其它临床磁共振图像中无法显示的白质病变.如图 4所示,我们根据初始空间标准化后的被试特征值及特征向量分别构建高斯DTI模板的FA图[图 4(a)]和线性DTI模板的FA图[图 4(b)]、高斯DTI模板的MD图[图 4(c)]和线性DTI模板的MD图[图 4(d)],以及高斯DTI模板对应的扩散加权图像[图 4(e)]和线性DTI模板对应的扩散加权图像[图 4(f)].由高斯DTI模板和线性DTI模板的FA图、MD图及对应的扩散加权图像三组图像对比,可以看出相对于高斯模板,线性模板在边界处过于平滑导致边缘模糊,降低了灰质和白质的分辨率.结合图 3可知高斯模板在灰质和白质边界处能保留更多结构细节.
图4
图4
(a) 和(c)高斯DTI模板的FA和MD图;(b)和(d)线性DTI模板的FA和MD图;(e)高斯DTI模板对应的扩散加权图像;(f)线性DTI模板对应的扩散加权图像
Fig.4
(a) and (c) FA and MD maps of Gaussian DTI template; (b) and (d) FA and MD maps of linear DTI template; (e) DWI corresponding to Gaussian DTI template; (f) DWI corresponding to linear DTI template
2.2 高斯模板和线性模板的评估参数比较
DTI模板体现了大脑中白质区域的微观结构信息,因此在进行图像评估前对FA图设定一个阈值,以便更好地观察两幅FA图在白质区域的差异.在这个阈值范围之内可以认为是大脑白质的区域.图 5所示的是选取阈值为0.2的掩膜.
图5
图5
(a) 高斯FA模板(原被试FA图做高斯平均得到)的掩膜;(b)线性FA模板(原被试FA图做线性平均得到)的掩膜
Fig.5
(a) Gaussian averaged FA template mask. (b) Linearly averaged FA template mask
表1 通过高斯FA模板和线性FA模板进行空间标准化前后的FA图之间的关联性(corrFA值)
Table 1
| 被试编号 | linear | Gauss |
| 1 | 0.568 | 0.733 |
| 2 | 0.643 | 0.664 |
| 3 | 0.620 | 0.667 |
| 4 | 0.627 | 0.674 |
| 5 | 0.605 | 0.684 |
| 6 | 0.610 | 0.630 |
| 7 | 0.674 | 0.627 |
| 8 | 0.606 | 0.708 |
| 9 | 0.608 | 0.710 |
| 10 | 0.639 | 0.669 |
| 11 | 0.629 | 0.690 |
| 12 | 0.607 | 0.639 |
| 13 | 0.618 | 0.634 |
| 14 | 0.652 | 0.659 |
| 15 | 0.608 | 0.620 |
| 16 | 0.641 | 0.689 |
| 17 | 0.674 | 0.675 |
| 18 | 0.604 | 0.618 |
| 19 | 0.637 | 0.668 |
| 20 | 0.591 | 0.605 |
| 21 | 0.659 | 0.733 |
| 22 | 0.624 | 0.629 |
| 23 | 0.631 | 0.632 |
| 24 | 0.630 | 0.687 |
| 25 | 0.645 | 0.647 |
| 26 | 0.677 | 0.712 |
| 27 | 0.597 | 0.659 |
| 28 | 0.669 | 0.692 |
| 29 | 0.653 | 0.662 |
| 30 | 0.610 | 0.683 |
| 31 | 0.638 | 0.685 |
| 32 | 0.627 | 0.675 |
| 33 | 0.613 | 0.661 |
| 34 | 0.607 | 0.671 |
| 35 | 0.627 | 0.652 |
| 36 | 0.616 | 0.634 |
| 37 | 0.667 | 0.669 |
| 38 | 0.604 | 0.688 |
| 39 | 0.607 | 0.616 |
| 40 | 0.633 | 0.636 |
| 41 | 0.679 | 0.685 |
| 42 | 0.626 | 0.690 |
| 43 | 0.688 | 0.690 |
| 44 | 0.608 | 0.637 |
| 45 | 0.653 | 0.657 |
| 46 | 0.628 | 0.651 |
| 47 | 0.693 | 0.698 |
| 48 | 0.698 | 0.760 |
| 49 | 0.683 | 0.698 |
| 50 | 0.664 | 0.719 |
| 51 | 0.619 | 0.650 |
| 52 | 0.669 | 0.689 |
| 53 | 0.607 | 0.608 |
| 54 | 0.627 | 0.653 |
| 55 | 0.682 | 0.696 |
| 平均值±标准差 | 0.635±0.030 | 0.668±0.033 |
为更全面地比较两种模板,将55名被试分别配准到高斯DTI模板和线性DTI模板上得到空间标准化后的DTI数据,并分别计算其与空间标准化前的DTI数据之间的各项评估参数,其中
表2 脑模板参数评估
Table 2
| 被试编号 | DTED/(×104) | COH | DVED/(×105) | OVL | corrFA/(×10−1) | |||||||||
| Gauss | linear | Gauss | linear | Gauss | linear | linear | Gauss | linear | ||||||
| 1 | 0.141±0.428 | 3.83±10.2 | 0.029±0.055 | 0.026±0.061 | 2.61±7.93 | 44.6±126 | 0.152±2.80 | 0.148±4.38 | 6.31 | 6.30 | ||||
| 2 | 0.128±0.396 | 3.81±10.1 | 0.084±0.024 | 0.028±0.053 | 2.65±8.01 | 44.6±126 | 0.156±2.65 | 0.151±8.91 | 7.14 | 7.13 | ||||
| 3 | 0.131±0.397 | 3.82±10.2 | 0.026±0.056 | 0.091±0.036 | 2.70±8.15 | 44.7±130 | 0.145±2.30 | 0.142±2.87 | 6.70 | 6.69 | ||||
| 4 | 0.128±0.391 | 3.82±10.2 | 0.045±0.058 | 0.028±0.031 | 2.65±7.98 | 44.7±126 | 0.150±4.36 | 0.118±43.3 | 6.98 | 6.97 | ||||
| 5 | 0.130±0.397 | 3.83±10.2 | 0.037±0.036 | 0.031±0.022 | 2.67±8.05 | 44.7±126 | 0.155±1.24 | 0.158±2.78 | 6.84 | 6.83 | ||||
| 6 | 0.128±0.393 | 3.83±10.2 | 0.054±0.023 | 0.041±0.041 | 2.84±8.62 | 44.8±127 | 0.140±1.34 | 0.139±2.67 | 6.61 | 6.60 | ||||
| 7 | 0.123±0.380 | 3.84±10.2 | 0.023±0.010 | 0.139±0.025 | 2.74±8.29 | 44.7±126 | 0.148±1.19 | 0.147±0.95 | 7.11 | 7.10 | ||||
| 8 | 0.131±0.400 | 3.83±10.2 | 0.050±0.063 | 0.080±0.036 | 2.70±8.17 | 44.7±126 | 0.141±6.34 | 0.155±15.1 | 6.74 | 6.73 | ||||
| 9 | 0.133±0.407 | 3.82±10.2 | 0.047±0.050 | 0.033±0.058 | 2.65±8.00 | 44.7±126 | 0.148±5.28 | 0.151±0.24 | 6.83 | 6.82 | ||||
| 10 | 0.123±0.380 | 3.82±10.1 | 0.142±0.008 | 0.010±0.026 | 2.77±8.34 | 44.8±127 | 0.148±1.18 | 0.147±0.72 | 7.09 | 7.08 | ||||
| 11 | 0.101±0.342 | 3.86±10.1 | 0.138±0.025 | 0.101±0.062 | 2.71±8.91 | 44.7±127 | 0.164±3.53 | 0.100±7.95 | 6.58 | 6.35 | ||||
| 12 | 0.129±0.337 | 3.88±10.1 | 0.096±0.036 | 0.051±0.051 | 2.83±7.03 | 44.5±127 | 0.143±4.53 | 0.126±8.53 | 6.29 | 5.65 | ||||
| 13 | 0.156±0.382 | 3.81±10.2 | 0.122±0.008 | 0.045±0.039 | 2.62±8.63 | 44.7±126 | 0.167±5.52 | 0.143±7.85 | 6.42 | 5.07 | ||||
| 14 | 0.140±0.392 | 3.90±10.1 | 0.060±0.028 | 0.052±0.065 | 2.79±8.12 | 44.5±127 | 0.154±3.09 | 0.123±5.32 | 5.84 | 5.48 | ||||
| 15 | 0.144±0.309 | 3.84±10.1 | 0.093±0.021 | 0.060±0.013 | 2.59±7.47 | 44.6±127 | 0.140±2.57 | 0.130±0.24 | 7.32 | 6.91 | ||||
| 16 | 0.109±0.307 | 3.87±10.2 | 0.064±0.025 | 0.039±0.034 | 2.82±8.25 | 44.6±127 | 0.180±5.44 | 0.160±1.38 | 8.88 | 6.20 | ||||
| 17 | 0.129±0.348 | 3.85±10.2 | 0.147±0.024 | 0.116±0.058 | 2.56±8.17 | 44.8±127 | 0.167±5.32 | 0.150±10.9 | 8.22 | 7.53 | ||||
| 18 | 0.127±0.336 | 3.71±10.1 | 0.105±0.043 | 0.124±0.069 | 2.84±7.26 | 44.8±127 | 0.158±5.42 | 0.155±8.95 | 7.25 | 6.31 | ||||
| 19 | 0.151±0.325 | 3.83±10.2 | 0.192±0.041 | 0.131±0.014 | 2.50±7.34 | 44.7±127 | 0.162±4.44 | 0.122±6.68 | 7.36 | 5.01 | ||||
| 20 | 0.109±0.388 | 3.74±10.2 | 0.102±0.042 | 0.093±0.065 | 2.42±8.71 | 44.7±127 | 0.144±6.24 | 0.142±2.03 | 8.16 | 5.01 | ||||
| 21 | 0.105±0.331 | 3.77±10.2 | 0.092±0.030 | 0.100±0.024 | 2.89±8.48 | 44.7±126 | 0.164±5.94 | 0.129±8.58 | 8.69 | 7.94 | ||||
| 22 | 0.146±0.377 | 3.89±10.2 | 0.119±0.009 | 0.040±0.060 | 2.80±8.77 | 44.6±127 | 0.140±4.00 | 0.112±8.26 | 6.93 | 6.56 | ||||
| 23 | 0.103±0.327 | 3.80±10.2 | 0.128±0.015 | 0.039±0.036 | 2.55±7.38 | 44.8±127 | 0.145±4.77 | 0.124±4.26 | 8.26 | 5.26 | ||||
| 24 | 0.156±0.334 | 3.71±10.1 | 0.119±0.058 | 0.090±0.043 | 2.59±7.85 | 44.7±126 | 0.143±7.00 | 0.112±9.71 | 8.61 | 6.49 | ||||
| 25 | 0.153±0.353 | 3.71±10.2 | 0.115±0.014 | 0.048±0.029 | 2.44±7.40 | 44.5±126 | 0.156±5.54 | 0.121±6.75 | 7.07 | 5.42 | ||||
| 26 | 0.131±0.308 | 3.87±10.1 | 0.120±0.068 | 0.019±0.031 | 2.73±8.47 | 44.8±126 | 0.129±1.49 | 0.112±0.01 | 7.42 | 6.84 | ||||
| 27 | 0.145±0.334 | 3.70±10.1 | 0.108±0.029 | 0.044±0.014 | 2.43±7.54 | 44.8±127 | 0.144±4.53 | 0.123±14.9 | 7.18 | 5.40 | ||||
| 28 | 0.139±0.317 | 3.72±10.1 | 0.071±0.020 | 0.057±0.020 | 2.83±7.56 | 44.5±126 | 0.141±4.94 | 0.124±2.40 | 7.06 | 5.92 | ||||
| 29 | 0.148±0.358 | 3.88±10.1 | 0.071±0.031 | 0.037±0.049 | 2.42±7.47 | 44.8±126 | 0.168±3.14 | 0.133±9.15 | 8.99 | 7.98 | ||||
| 30 | 0.143±0.373 | 3.70±10.0 | 0.078±0.052 | 0.023±0.068 | 2.67±8.10 | 44.9±127 | 0.157±1.20 | 0.147±3.91 | 7.71 | 6.79 | ||||
| 31 | 0.135±0.363 | 3.77±10.2 | 0.047±0.056 | 0.046±0.012 | 2.77±7.37 | 44.8±126 | 0.164±2.98 | 0.126±13.1 | 8.22 | 5.29 | ||||
| 32 | 0.155±0.348 | 3.79±10.1 | 0.065±0.031 | 0.012±0.019 | 2.41±7.28 | 44.8±126 | 0.129±3.88 | 0.131±12.0 | 7.93 | 5.66 | ||||
| 33 | 0.154±0.386 | 3.87±10.1 | 0.078±0.045 | 0.053±0.019 | 2.43±7.95 | 44.6±126 | 0.167±3.67 | 0.145±0.51 | 6.71 | 5.64 | ||||
| 34 | 0.140±0.350 | 3.76±10.1 | 0.078±0.037 | 0.025±0.048 | 2.81±8.49 | 44.8±126 | 0.133±2.14 | 0.110±4.14 | 7.72 | 7.36 | ||||
| 35 | 0.119±0.334 | 3.73±10.1 | 0.060±0.023 | 0.028±0.059 | 2.67±7.63 | 44.8±126 | 0.147±6.51 | 0.103±13.5 | 7.15 | 5.59 | ||||
| 36 | 0.134±0.346 | 3.79±10.2 | 0.116±0.057 | 0.042±0.043 | 2.82±8.31 | 44.6±127 | 0.156±2.83 | 0.155±7.21 | 7.95 | 6.31 | ||||
| 37 | 0.111±0.317 | 3.77±10.1 | 0.065±0.029 | 0.063±0.067 | 2.45±8.75 | 44.9±126 | 0.147±4.15 | 0.128±8.15 | 6.49 | 5.36 | ||||
| 38 | 0.119±0.330 | 3.76±10.2 | 0.112±0.045 | 0.053±0.034 | 2.45±7.38 | 44.5±127 | 0.157±2.48 | 0.157±12.9 | 8.24 | 7.68 | ||||
| 39 | 0.148±0.362 | 3.72±10.1 | 0.082±0.019 | 0.021±0.016 | 2.72±8.93 | 44.6±127 | 0.131±2.08 | 0.115±14.8 | 8.91 | 6.90 | ||||
| 40 | 0.117±0.341 | 3.82±10.1 | 0.116±0.007 | 0.036±0.054 | 2.89±8.79 | 44.5±126 | 0.138±2.21 | 0.136±3.82 | 7.82 | 5.62 | ||||
| 41 | 0.120±0.385 | 3.81±10.1 | 0.106±0.009 | 0.102±0.048 | 2.62±7.47 | 44.7±126 | 0.154±5.13 | 0.141±7.91 | 6.20 | 6.12 | ||||
| 42 | 0.107±0.315 | 3.73±10.1 | 0.057±0.056 | 0.039±0.027 | 2.44±8.07 | 44.5±126 | 0.147±1.55 | 0.128±3.60 | 6.36 | 6.22 | ||||
| 43 | 0.134±0.302 | 3.85±10.2 | 0.100±0.053 | 0.064±0.063 | 2.50±8.16 | 44.7±127 | 0.125±3.48 | 0.105±13.1 | 7.86 | 5.95 | ||||
| 44 | 0.149±0.323 | 3.70±10.1 | 0.136±0.034 | 0.093±0.031 | 2.41±7.63 | 44.6±127 | 0.150±3.10 | 0.129±9.21 | 7.52 | 6.17 | ||||
| 45 | 0.123±0.353 | 3.79±10.2 | 0.088±0.011 | 0.052±0.018 | 2.45±8.37 | 44.8±127 | 0.168±2.52 | 0.147±5.73 | 6.88 | 6.40 | ||||
| 46 | 0.142±0.389 | 3.86±10.1 | 0.128±0.045 | 0.034±0.061 | 2.67±8.76 | 44.7±126 | 0.144±3.27 | 0.127±11.2 | 8.25 | 7.54 | ||||
| 47 | 0.143±0.339 | 3.76±10.1 | 0.114±0.018 | 0.102±0.063 | 2.84±8.38 | 44.7±126 | 0.142±4.46 | 0.117±6.08 | 7.17 | 6.00 | ||||
| 48 | 0.153±0.335 | 3.74±10.1 | 0.091±0.045 | 0.085±0.061 | 2.70±7.17 | 44.9±127 | 0.158±6.75 | 0.111±9.43 | 8.02 | 5.59 | ||||
| 49 | 0.103±0.327 | 3.77±10.1 | 0.115±0.018 | 0.057±0.058 | 2.82±8.32 | 44.7±126 | 0.168±3.25 | 0.146±4.33 | 6.38 | 5.59 | ||||
| 50 | 0.151±0.385 | 3.80±10.2 | 0.081±0.054 | 0.034±0.038 | 2.89±7.81 | 44.8±127 | 0.180±6.90 | 0.170±11.6 | 8.62 | 8.54 | ||||
| 51 | 0.104±0.367 | 3.89±10.2 | 0.081±0.047 | 0.047±0.037 | 2.82±7.80 | 44.9±127 | 0.166±2.62 | 0.107±10.7 | 7.80 | 7.74 | ||||
| 52 | 0.146±0.363 | 3.84±10.2 | 0.024±0.011 | 0.017±0.023 | 2.54±8.21 | 44.6±127 | 0.167±2.14 | 0.124±9.07 | 6.27 | 5.14 | ||||
| 53 | 0.138±0.345 | 3.87±10.1 | 0.110±0.021 | 0.020±0.043 | 2.83±8.20 | 44.9±126 | 0.157±4.31 | 0.153±6.69 | 7.50 | 5.07 | ||||
| 54 | 0.121±0.344 | 3.73±10.1 | 0.087±0.053 | 0.073±0.067 | 2.42±7.17 | 44.7±127 | 0.166±3.10 | 0.162±11.6 | 8.26 | 5.00 | ||||
| 55 | 0.112±0.331 | 3.80±10.1 | 0.108±0.024 | 0.033±0.043 | 2.49±8.26 | 44.6±127 | 0.128±6.65 | 0.116±10.7 | 6.77 | 6.65 | ||||
| 平均值±标准差 | 0.132±0.016 | 3.80±0.058 | 0.089±0.035 | 0.055±0.032 | 2.65±0.156 | 44.7±0.116 | 0.152±0.013 | 0.133±0.017 | 7.37±0.802 | 6.32±0.880 | ||||
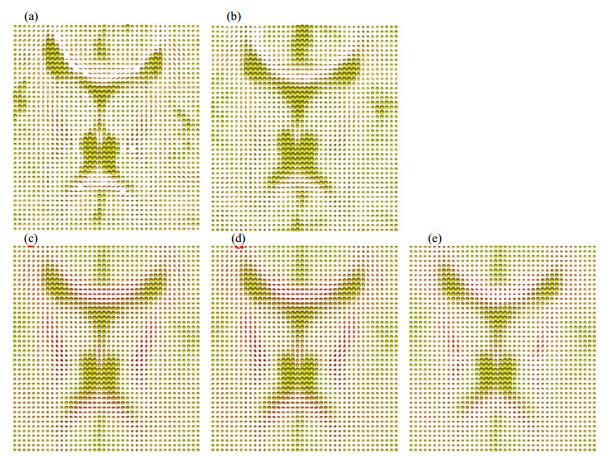
在一定程度上,DTI脑模板能够体现人脑单个体素的信息,对于比较神经元结构的完整性和群体间的脑连接性具有重要价值.图 6(a)为一例被试的原始张量;图 6(b)为该被试配准到初始模板后计算得到的张量;图 6(c)为将所有经过初始空间标准化后被试的张量直接进行线性平均得到的模板张量(无四元数引入的线性张量模板);图 6(d)为将经过初始空间标准化的被试的张量分解为特征向量及特征值后,将特征向量转化为四元数,对四元数做线性平均并反变换为特征向量,之后与线性平均后的特征值进行重建得到的模板张量(即线性张量模板);图 6(e)为本文构建的高斯模板的张量.图 6显示将被试配准到初始模板后,部分缺失的张量被填充,并且沿着白质走向的张量被平滑.图 6(c)和图 6(d)之间的张量变化不大,而与图 6(e)有一定差异,表明引入高斯加权对张量方向信息有一定影响,而四元数对方向信息的影响不明显.图 6(c)~6(e)与图 6(a)和6(b)的张量走向差异都较大,表明张量平均的方法对张量方向信息影响较大,具体影响参照表 3.
图6
图6
张量的可视化.(a)一例被试的原始张量;(b)该被试经初始模板配准后的张量;(c)所有被试张量经初始模板配准后,直接线性平均后的模板张量(无四元数引入的线性模板的张量);(d)线性模板的张量;(e)高斯模板的张量
Fig.6
Visualization of the tensor. (a) Original tensor of the subject; (b) Tensor of the subject after registration to the initial template; (c) Tensor of linear template without quaternion conversion; (d) Tensor of linear template; (e) Tensor of Gaussian template
表3 通过高斯DTI模板与线性DTI模板进行空间标准化前后张量的IA参数比较
Table 3
| 被试编号 | Gauss | linear | linear2 |
| 1 | 0.146±0.785 | 0.115±0.794 | 0.126±0.778 |
| 2 | 0.146±0.806 | 0.118±0.810 | 0.126±0.821 |
| 3 | 0.158±0.869 | 0.125±0.871 | 0.137±0.887 |
| 4 | 0.153±0.912 | 0.125±0.919 | 0.135±0.915 |
| 5 | 0.149±0.894 | 0.117±0.899 | 0.128±0.899 |
| 6 | 0.162±0.871 | 0.130±0.877 | 0.140±0.880 |
| 7 | 0.154±0.953 | 0.123±0.957 | 0.130±0.955 |
| 8 | 0.155±0.794 | 0.124±0.799 | 0.130±0.798 |
| 9 | 0.148±0.844 | 0.117±0.848 | 0.127±0.850 |
| 10 | 0.146±0.915 | 0.116±0.918 | 0.128±0.911 |
| 11 | 0.151±0.649 | 0.135±0.792 | 0.109±0.704 |
| 12 | 0.142±0.603 | 0.120±0.724 | 0.114±0.719 |
| 13 | 0.146±0.689 | 0.119±0.606 | 0.129±0.618 |
| 14 | 0.170±0.826 | 0.131±0.853 | 0.129±0.910 |
| 15 | 0.135±0.761 | 0.113±0.743 | 0.120±0.916 |
| 16 | 0.155±0.907 | 0.122±0.714 | 0.117±0.897 |
| 17 | 0.140±0.927 | 0.126±0.938 | 0.117±0.609 |
| 18 | 0.137±0.730 | 0.102±0.838 | 0.115±0.903 |
| 19 | 0.151±0.833 | 0.114±0.739 | 0.128±0.663 |
| 20 | 0.148±0.776 | 0.134±0.645 | 0.140±0.716 |
| 21 | 0.167±0.668 | 0.121±0.897 | 0.105±0.765 |
| 22 | 0.155±0.640 | 0.135±0.887 | 0.126±0.803 |
| 23 | 0.155±0.793 | 0.113±0.872 | 0.140±0.806 |
| 24 | 0.150±0.627 | 0.103±0.939 | 0.109±0.700 |
| 25 | 0.139±0.864 | 0.117±0.967 | 0.109±0.606 |
| 26 | 0.166±0.739 | 0.139±0.721 | 0.109±0.983 |
| 27 | 0.166±0.914 | 0.137±0.757 | 0.122±0.783 |
| 28 | 0.160±0.879 | 0.114±0.914 | 0.136±0.880 |
| 29 | 0.142±0.995 | 0.131±0.608 | 0.137±0.736 |
| 30 | 0.150±0.773 | 0.129±0.723 | 0.110±0.911 |
| 31 | 0.162±0.847 | 0.117±0.740 | 0.131±0.880 |
| 32 | 0.157±0.787 | 0.116±0.672 | 0.109±0.633 |
| 33 | 0.136±0.691 | 0.128±0.606 | 0.113±0.655 |
| 34 | 0.155±0.947 | 0.101±0.698 | 0.108±0.820 |
| 35 | 0.142±0.695 | 0.110±0.994 | 0.124±0.608 |
| 36 | 0.133±0.911 | 0.131±0.805 | 0.110±0.758 |
| 37 | 0.136±0.840 | 0.114±0.771 | 0.106±0.854 |
| 38 | 0.156±0.801 | 0.101±0.797 | 0.129±0.872 |
| 39 | 0.160±0.762 | 0.113±0.987 | 0.104±0.605 |
| 40 | 0.151±0.892 | 0.120±0.624 | 0.129±0.999 |
| 41 | 0.143±0.773 | 0.136±0.931 | 0.122±0.722 |
| 42 | 0.152±0.884 | 0.108±0.635 | 0.113±0.620 |
| 43 | 0.154±0.752 | 0.109±0.855 | 0.131±0.842 |
| 44 | 0.142±0.681 | 0.133±0.757 | 0.118±0.770 |
| 45 | 0.148±0.853 | 0.107±0.989 | 0.104±0.702 |
| 46 | 0.144±0.708 | 0.108±0.656 | 0.102±0.899 |
| 47 | 0.154±0.807 | 0.111±0.947 | 0.119±0.670 |
| 48 | 0.147±0.771 | 0.118±0.978 | 0.113±0.957 |
| 49 | 0.156±0.653 | 0.101±0.948 | 0.116±0.654 |
| 50 | 0.145±0.662 | 0.112±0.829 | 0.130±0.909 |
| 51 | 0.153±0.998 | 0.122±0.890 | 0.124±0.722 |
| 52 | 0.136±0.685 | 0.123±0.894 | 0.118±0.772 |
| 53 | 0.132±0.646 | 0.124±0.782 | 0.126±0.636 |
| 54 | 0.154±0.638 | 0.108±0.653 | 0.117±0.708 |
| 55 | 0.143±0.677 | 0.121±0.895 | 0.121±0.678 |
| 平均值±标准差 | 0.150±0.009 | 0.119±0.010 | 0.121±0.010 |
经高斯DTI模板或线性DTI模板空间标准化前后的张量方向变化如表 3所示,表 3中Gauss一列显示了经高斯DTI模板配准前后张量的方向变化信息,linear一列显示经线性DTI模板配准前后张量的方向变化信息,linear2一列显示了经无四元数引入的线性DTI模板配准前后张量的方向变化信息.Gauss与linear差异显著(p < 0.01),linear与linear2差异不显著(p > 0.05),Gauss与linear2差异显著(p < 0.01).相对于高斯DTI模板,两种线性DTI模板配准前后张量的方向变化更小,可能是因为高斯加权对方向信息进行了平滑.而线性DTI模板的方向变化比直接将张量线性平均得到的模板更小,表明“将张量分解为标量后分别进行平均”这一操作在对张量中方向信息的保留上有所改善.
2.3 讨论
DTI人脑模板保留了整个大脑白质微结构特性的信息,对于跨人群白质微结构的基于体素的准确比较以及白质图谱的开发至关重要.相比线性模板,本文构建的高斯模板保留了更多的结构细节.
本研究优化了解决现有DTI脑模板构建时的两个问题的方案:(a)没有使用标准的脑模板作为基础配准,避免了因人种不同引起大脑配准时的变形而导致的误差;(b)使用高斯平均替代线性平均,在整体信息保留方面有所优化,但方向信息有所丢失.
另外该方法还有一些需要改进的地方.本文选取的被试的DTI数据均来源于数据库,该数据是通过EPI序列采集的.虽然我们已经采用数据预处理的方式将EPI序列可能产生的伪影以及失真的影响降低到最小,但实际上对于DTI脑模板的分辨率仍旧影响较大.因此在后续的研究中会考虑使用更优化的伪影消除方法.
3 结论
本文以国内人群的大脑作为研究对象,将高斯加权及四元数应用于DTI数据中.构建了基于DTI图像的多维度脑模板,该方法先将被试DTI数据配准到初始模板,然后使用高斯平均将数据平均到群空间中以生成平均脑模板.以BNU数据集中19~30岁的具有相似扩散特性的55名健康被试为研究对象,对本文方法进行了验证,结果显示,相较于线性DTI模板,本文提出的高斯DTI模板在DTED、COH、DVED、OVL、
无
参考文献
Estimation of the effective self-diffusion tensor from the NMR spin echo
[J].DOI:10.1006/jmrb.1994.1037 [本文引用: 1]
Diffusion-weighted MR imaging of anisotropic water diffusion in cat central nervous system
[J].DOI:10.1148/radiology.176.2.2367658 [本文引用: 1]
Diffusion tensor imaging: concepts and applications
[J].
Visualizing and characterizing white matter fiber structure and architecture in the human pyramidal tract using diffusion tensor MRI
[J].DOI:10.1016/S0730-725X(99)00048-X [本文引用: 1]
Diffusion tensor imaging in patients with epilepsy and malformations of cortical development
[J].DOI:10.1093/brain/124.3.617 [本文引用: 1]
White matter abnormalities in first-episode schizophrenia or schizoaffective disorder: a diffusion tensor imaging study
[J].DOI:10.1176/appi.ajp.162.3.602 [本文引用: 1]
White matter abnormalities in bipolar disorder: a voxel-based diffusion tensor imaging study
[J].DOI:10.1111/j.1399-5618.2007.00552.x [本文引用: 1]
Evolution of water diffusion and anisotropy in hyperacute stroke: significant correlation between fractional anisotropy and T2
[J].
Investigating the medial temporal lobe in Alzheimer's disease and mild cognitive impairment, with Turboprop diffusion tensor imaging, MRI-volumetry, and T2-relaxometry
[J].
Diffusion tensor MR imaging in diffuse axonal injury
[J].
Neuropathological abnormalities of the corpus callosum in schizophrenia: a diffusion tensor imaging study
[J].DOI:10.1136/jnnp.68.2.242 [本文引用: 1]
Diffusion tensor imaging of cryptogenic and acquired partial epilepsies
[J].DOI:10.1093/brain/124.3.627 [本文引用: 1]
Morphometry on diffusion tensor data
[J].DOI:10.1016/S1053-8119(01)91471-5 [本文引用: 1]
Reference-free brain template construction with population symmetric registration
[J].DOI:10.1007/s11517-020-02226-5 [本文引用: 1]
扩散张量图像的插值方法综述
[J].
A review on interpolation methods for diffusion tensor images
[J].
基于磁共振图像和改进的UNet++模型区分阿尔茨海默症患者和健康人群
[J].
Classification of Alzheimer's disease patients based on magnetic resonance images and an improved UNet++ model
[J].
Spectrum-sine interpolation framework for DTI processing
[J].DOI:10.1007/s11517-021-02471-2 [本文引用: 1]
扩散张量成像的人脑模板构建
[J].
Construction of human brain templates with diffusion tensor imaging data: a review
[J].
Spatial normalization and averaging of diffusion tensor MRI data sets
[J].DOI:10.1006/nimg.2002.1148 [本文引用: 1]
Spatial normalization of diffusion tensor MRI using multiple channels
[J].DOI:10.1016/j.neuroimage.2003.08.008 [本文引用: 1]
Preservation of diffusion tensor properties during spatial normalization by use of tensor imaging and fibre tracking on a normal brain database
[J].DOI:10.1088/0031-9155/52/6/N01 [本文引用: 1]
Stereotaxic white matter atlas based on diffusion tensor imaging in an ICBM template
[J].DOI:10.1016/j.neuroimage.2007.12.035 [本文引用: 1]
Development of a human brain diffusion tensor template
[J].DOI:10.1016/j.neuroimage.2009.03.046 [本文引用: 1]
Enhanced ICBM diffusion tensor template of the human brain
[J].DOI:10.1016/j.neuroimage.2010.09.008 [本文引用: 2]
Development of a high angular resolution diffusion imaging human brain template
[J].DOI:10.1016/j.neuroimage.2014.01.009 [本文引用: 1]
Multi-site genetic analysis of diffusion images and voxelwise heritability analysis: A pilot project of the ENIGMA-DTI working group
[J].
Estimating topology preserving and smooth displacement fields
[J].DOI:10.1109/TMI.2004.827963 [本文引用: 1]