引言
直肠癌发病率约占全部结直肠癌的30%,其早期诊断对于患者治疗方案的制定极其重要.根据美国国家综合癌症网络(National Comprehensive Cancer Network,NCCN)直肠癌临床实践指南[6],早期(T1~T2N0)直肠癌患者可以直接进行手术切除肿瘤;局部进展期(T3~T4)及伴有区域淋巴结转移的T1、T2期(T1~T2N+)直肠癌患者则需要在手术前进行新辅助放化疗,降低分期后再进行手术,从而达到提高肿瘤的可切除性、改善患者生存质量、降低术后局部复发率的目的.因此,准确的早期诊断与临床决策可以为患者提供精准的个性化治疗方案,显著降低直肠癌死亡率.在直肠癌的临床诊断中,磁共振成像(Magnetic Resonance Imaging,MRI)具有不可替代的优势,可完成多角度、多参数和多序列的成像,软组织的分辨率高,可对直肠壁的结构、肠壁浸润深度进行显示.
传统的影像科医生主观评估磁共振图像方法缺乏量化的标准,且时间消耗大,随着直肠癌发病率的不断升高,医生的工作量也不断增加,因此利用影像组学(Radiomics)技术来辅助临床诊断显得尤为重要.影像组学由荷兰学者Lambin等[7]在2012年提出,是一种新型的通过分析影像数据获得影像信息的方法.它首先进行病灶分割,然后从影像资料中高通量获取影像信息,再对提取得到的信息进行特征提取与筛选,并建立模型,这样可以有效解决肿瘤内部由于异质性导致的难以定量评估的问题.凭借对海量影像数据信息进行更深层次的挖掘来帮助医生作出更准确的诊断,具有重要的临床意义.影像组学常见的建模方法可分为两类:一种是手工设计特征的传统机器学习方法,包括支持向量机(Support Vector Machine,SVM,也称为支持向量网络)、逻辑回归(Logistic Regression)、随机森林(Random Forest)等算法;另一种是自动提取影像特征的深度学习方法,如卷积神经网络(Convolutional Neural Networks,CNN),需要较大的训练集数据,否则容易过拟合.
目前,对于直肠癌T分期的研究普遍采用轴位高分辨率磁共振图像,但是对于有MRI禁忌症的患者,也可以使用电子计算机断层扫描(Computed Tomography,CT)增强扫描.徐从斌[8]选择了31例经手术验证为直肠癌患者的磁共振图像与CT图像数据,发现磁共振图像的确诊率优于CT图像.崔书发等[9]研究表明术前MRI评价直肠癌T分期的准确率高、一致性强、应用价值高;且身高体重指数(Body Mass Index,BMI)越小,术前MRI评价直肠癌T分期的准确率可能越高.Liang等[10]使用最小绝对值收敛和选择算子(Least Absolute Shrinkage and Selection Operator,LASSO)回归模型对494例直肠癌患者的CT增强图像应用影像组学方法分析,获得了良好的受试者操作特征曲线(Receiver Operating Characteristic curve,ROC),ROC曲线下面积(Area Under Curve,AUC)为0.792.Dou等[11]使用基于LASSO算法的逻辑回归对29例直肠癌患者的磁共振图像建模预测,十折交叉验证下的AUC均值为0.85.Kim等[12]使用卷积神经网络先进行了直肠癌肿瘤的自动分割,再使用一个新网络学习了肿瘤的位置信息,并进行肿瘤T2/T3期的分类.Xu等[13]使用了SVM算法对71例膀胱癌患者复发状况进行了影像组学分析,获得了88%的准确率和0.915的AUC.影像科医生通过磁共振图像主观评估T分期的准确率约为70%.基于影像组学的直肠癌T分期准确度虽然高于医生主观评估,但还有待提升.
本文的目的是通过影像组学方法对直肠癌患者的磁共振图像进行深度挖掘,精准预测直肠肿瘤的T分期.本文综合使用了随机森林(Random Forest)、SVM、逻辑回归(Logistic Regression)、梯度提升树(Gradient Boosting Decision Tree,GBDT)四种传统机器学习算法建模:通过对随机森林的子树数量,SVM的核函数以及函数的系数,逻辑回归的惩罚项及其系数,GBDT的迭代次数、学习率、随机程度等进行详细优化,实现了较高的直肠癌T分期准确率预测.上述分类算法皆属于传统机器学习方法,与深度学习的方法相比,在小样本的数据集上拟合效果更好,资源消耗低、计算效率高.
1 实验数据与方法
影像组学流程如图 1所示,包含了影像数据获取、病灶分割、影像组学特征提取、特征选择和数据建模五个阶段.
图1
1.1 影像数据获取
从2016年9月至2019年1月复旦大学附属肿瘤医院的影像归档和通信系统(Picture Archiving and Communication Systems,PACS)中将原始的DICOM格式影像数据下载到本地,每个患者的影像数据分别存在单独文件夹中.共纳入105例直肠癌患者,包含75例男性和30例女性,年龄为33~71岁,平均年龄为54.8岁.术后病理报告显示T1、T2期患者31例(未突破肌层组),T3、T4期患者74例(突破肌层组).本文研究内容所用数据都得到患者事先同意.所有患者MRI检查前4 h禁食,使用开塞露清洁肠道.MRI扫描使用Siemens MAGNETOM Skyra 3T MRI系统和腹部相控阵线圈,均采用斜横断面高分辨T2WI序列,扫描平面垂直于病灶所在肠管的长轴.扫描参数如下:图像矩阵大小为320×320,视野(Field of Vision,FOV)为18 cm×18 cm,重复时间(Repetition Time,TR)为4 000 ms,回波时间(Echo Time,TE)为108 ms,层厚为3 mm,层间距为2 mm,每例数据包含20~28层,反转角度为150˚,带宽为108 Hz/像素.
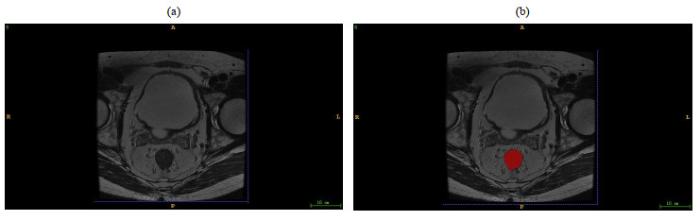
1.2 病灶分割
图2
图2
患者的(a) T2WI图像及(b)勾画后的ROI区域
Fig.2
(a) T2WI image (b) and the region of interest of one patient
1.3 影像组学特征提取
将上述数据用Python(V 3.6)打开,在jupyter notebook中使用pyradiomics工具包(V 2.1,美国俄勒冈州比佛顿Python软件基金会)[14]提取了四类影像组学特征:第一类特征为一阶统计量(First Order Statistics)计算出的肿瘤强度特征;第二类为肿瘤的形状特征,包括了肿瘤的体积、表面积、球形度、最大2D直径等;第三类为肿瘤的纹理特征,在肿瘤内的所有三维方向上计算,从而得出每个体素与周围体素相对的空间位置;第四类为原图像中小波分解计算得到的强度、纹理特征.
1.4 特征选择
由于提取的特征维数过高,直接进行机器学习容易过拟合,浪费计算资源,需要对其进行降维处理,选出与直肠癌T分期高度相关的特征.常用的降维算法有主成分分析法(Principal Component Analysis,PCA)、最小冗余最大相关性(Minimum Redundancy Maximum Correlation,mRMR)、LASSO回归、递归特征消除(Recursive Feature Elimination,RFE).
其中,LASSO属于嵌入法(Embedded),先使用机器学习算法进行训练,得到各个特征的权值系数,并按照系数大小进行特征选择.使用L1范数作为线性模型的惩罚项,模型会得到稀疏解,将部分特征的系数降维为0,系数不为0的特征则是特征选择后的结果.LASSO算法对高维数据的筛选有较好的效果,因此在影像组学中被广泛使用.
1.5 数据建模
常用的分类模型算法有随机森林、SVM、逻辑回归、GBDT等.
1.5.1 随机森林算法
随机森林属于有监督学习算法,是以决策树为基学习器的袋装法集成学习算法[15].首先通过对训练数据集的随机选择来构建一棵树,同时随机选择特征,最后对所有决策树的结果进行平均或者投票表决获得结果.随机森林易于实现,计算消耗较小,在解决分类问题与回归问题上都有惊人的表现,因此被称为是“最能体现集成学习技术水平的方法”.
随机森林的构建包含以下步骤[16]:第一步,从含有n个原始训练集中有放回采样(bootstrap)取出n个样本,生成一个训练集,由这种方法生成的自助集大约只包含原始数据的63%(因为每一个样本被抽到自助集的概率为
1.5.2 SVM算法
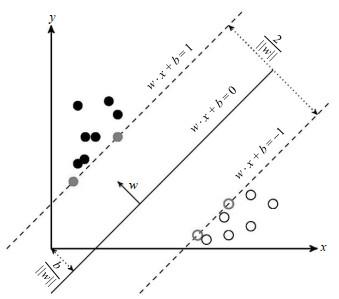
SVM是机器学习中最受关注的算法,源于统计学习理论[17],无论是对于线性还是非线性的分类问题,都有很好的效果,在各类实际问题中也表现优异,广泛应用于手写数字识别、人脸识别.在文本和超文本分类时,SVM可以大量减少标准归纳和转换设置中对标记训练实例的需求.SVM的基本思想是找出能够正确划分训练数据集[18]并且与之间隔最大的分离超平面.如图 3所示,黑点表示属于类别1的数据;灰点表示属于类别1且在支持向量上的数据;黑色圆圈表示属于类别2的数据;灰色圆圈表示属于类别2且在支持向量上的数据;虚线表示支持平面;实线(
图3
SVM算法推导过程如下[19]:假设存在数据集
(1)选择惩罚参数
得最优解:
(2)计算
选择
(3)求分离超平面:
分类决策函数:
对于非线性分类问题,可以通过非线性变换将之转换为某个空间上的线性分类问题,并在此空间中学习线性SVM.在线性SVM的对偶问题中,目标函数与分类决策函数只涉及实例与实例的内积,所以不需要指定非线性变换,而是用核函数替换当中的内积.核函数是指通过一个非线性转换后的两个实例间的内积.具体的说,
在线性SVM学习的对偶问题中,用
1.5.3 逻辑回归算法
图4
其中
1.5.4 GBDT算法
GBDT又名MART(Multiple Additive Regression Tree),是一种boosting型的集成学习算法[23],它的基学习器是按顺序一一构建的.通过结合弱学习器的能力不断对难学习的样本进行预测,逐渐构建一个强学习器.GBDT具有同SVM一样较强的泛化(generalization)能力,近年来被广泛使用在搜索排序等领域.与随机森林不同的是,不论是回归还是分类,GBDT都使用CART(Classification and Regression Trees)回归树作为基学习器.这是因为GBDT每轮训练都建立在上一轮训练模型梯度为负的基础上.这就要求在每轮迭代中,标签值减去弱分类器的输出是有意义的.而类别相减是无意义的,因此使用CART进行预测,通过Sigmoid函数将回归值转化为概率值,将其与真实概率值之差作为拟合项.GBDT二分类算法实现过程如下[24]:
(1)初始化第一个弱学习器
其中
(2)建立M棵分类回归树
a)对
b)对于
c)对于叶子节点区域,计算最佳拟合值:
d)更新强学习器
(3)得到最终强学习器表达式:
因此分类模型为:
1.6 评价方法
将数据随机分为4:1的训练集与测试集比例(训练集84例,测试集21例)进行学习,计算十折交叉验证后的直肠癌T分期预测模型的准确率(Accuracy)、灵敏度(Sensitivity)、特异度(Specificity)、ROC曲线的AUC.
其中TP表示为真阳性,表示被判定为突破肌层、实际也是突破肌层的个数;TN表示为真阴性,表示被判定为未突破肌层、实际也是未突破肌层的个数;FP表示为假阳性,表示被判定为突破肌层、实际是未突破肌层的个数;FN表示为假阴性,表示被判定为未突破肌层、实际是突破肌层的个数.
ROC曲线是常用的分类模型的评价方法.其基本思想是通过对模型预测结果的排序,按顺序将样本作为阳性再次预测,计算出灵敏度与特异度,以灵敏度为纵坐标、1-特异度为横坐标绘制ROC曲线.AUC越接近1,则模型越准确.
2 结果与讨论
2.1 基于LASSO的特征选择结果
共提取了100个影像组学特征,使用LASSO算法进行特征选择,应用正则化路径的方法在1×10−12~0.1之间搜索最优化λ的值为0.05(λ表示L1范数的惩罚力度),此时系数不为0的特征如表 1所示.
表1 特征选择结果
Table 1
| 特征名称 | 系数 | 特征详情 |
| 灰度相关矩阵高灰度依赖程度(original_gldm_LargeDependenceHighGrayLevelEmphasis) | 0.0318 | 灰度相关矩阵高灰度依赖程度 |
| 伸长率(original_shape_Elongation) | 0.0043 | ROI形状中两个最大的主成分之间的关系 |
| 平面度(original_shape_Flatness) | −0.0448 | ROI形状中最大和最小主成分之间的关系 |
| 最大2D直径(列)(original_shape_Maximum2DDiameterColumn) | 0.0616 | 冠状平面中肿瘤表面网格顶点之间最大的欧几里得距离 |
| 最大2D直径(切片)(original_shape_Maximum2DDiameterSlice) | 0.0431 | 轴向平面中肿瘤表面网格顶点之间最大的欧几里得距离 |
| 短轴长(original_shape_MinorAxisLength) | 0.1205 | 包围ROI的椭球的第二轴长 |
| 表面积与体积之比(original_shape_SurfaceVolumeRatio) | −0.0384 | 较低的值表示更紧凑的球形形状 |
2.2 各模型预测结果
2.2.1 基于随机森林的直肠癌T分期预测模型
本文使用Python中的第三方机器学习包sklearn[25]进行建模.使用sklearn中的RandomForestClassifier类来构建随机森林分类模型,并且基于泛化误差对模型调参,提高模型的精度.
随机森林主要的参数有n_estimators(子树的数量)、max_depth(树的最大生长深度)、min_samples_leaf(叶子的最小样本数量)、min_samples_split(分支节点的最小样本数量)、max_features(最大选择特征数).其中n_estimators对模型的影响最大,因此优先对其进行调整.
图5
图5
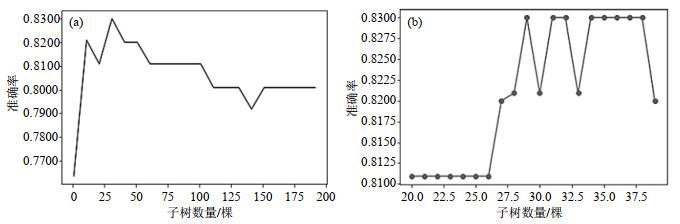
n_estimators在(a) 0~200和(b) 20~40间的学习曲线
Fig.5
Learning curves with n_estimators of (a) 0~200 and (b) 20~40
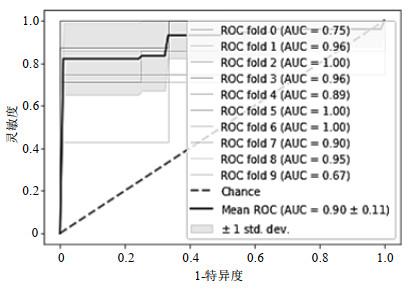
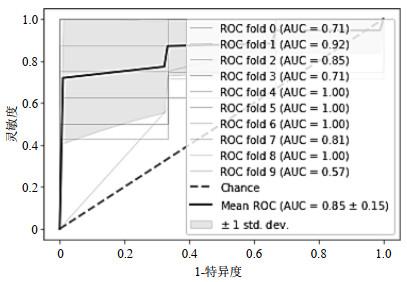
从学习曲线中可以看出在n_estimators取29时就达到了最高准确率0.830 0,相较于n_estimators=31时降低了模型复杂度,减少了计算消耗.因此将n_estimators设置为29,建模获得十折交叉验证后的平均AUC、准确率、灵敏度、特异度分别为0.901 5、0.830 0、0.910 7、0.869 0,获得的ROC曲线如图 6所示,测试集准确率达到了0.857 1.
图6
图6
基于随机森林的预测模型的ROC曲线
Fig.6
Receiver operating characteristic curve of the prediction model based on random forest
2.2.2 基于SVM的直肠癌T分期预测模型
使用sklearn工具包中的SVM类来搭建模型.kernel(核函数)是SVM算法中的一个重要参数:选用不同的核函数,可以寻找不同数据分布下的超平面.常用的核函数有线性核函数“linear”、多项式核函数“poly”、双曲正切核函数“sigmoid”、高斯径向基核函数“rbf”.在调参过程中,分别使用上述4个核函数进行建模,得到“linear”、“poly”、“sigmoid”、“rbf”四个核函数模型的准确率分别为0.828 2、0.867 3、0.876 4、0.810 9,因此本文选用“sigmoid”作为SVM模型的核函数.
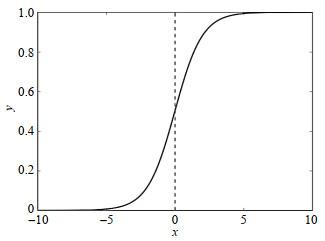
“sigmoid”是非线性函数,它的表达式为
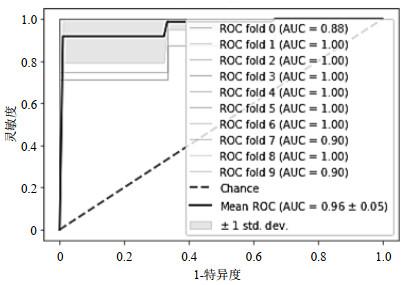
图7
图7
基于SVM的预测模型的ROC曲线
Fig.7
Receiver operation characteristic curve of the prediction model based on SVM
2.2.3 基于逻辑回归的直肠癌T分期模型预测
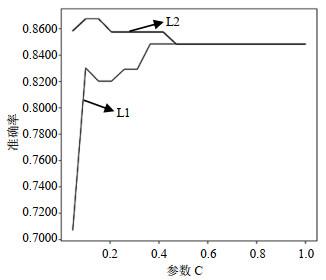
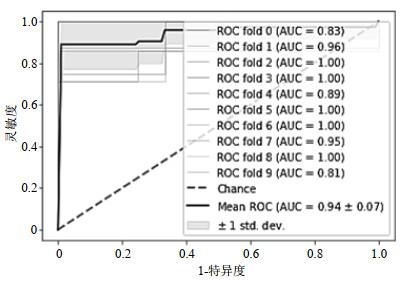
使用sklearn工具包中的LogisticRegression类来搭建模型,LogisticRegression算法中为了防止模型过拟合,需要在模型中加入penalty(惩罚项),提高模型的泛化能力.LogisticRegression的重要参数有penalty(惩罚项)以及正则化系数的倒数C,在建模过程中,需要进行调参优化.将参数C的范围设置为0.05~1,间隔大小为0.05,分别使用L1和L2正则化绘制学习曲线,如图 8所示,选用L2正则化的模型准确度高于选用L1正则化的模型,在C=0.1时,L2正则化模型准确率为0.847 6,达到了最高.因此选用参数penalty=“L2”、C=0.1构建模型,得到ROC曲线(图 9).模型的十折交叉验证后的平均AUC、准确率、灵敏度、特异度为0.943 9、0.847 6、0.905 7、0.889 4,测试集准确率达到了0.857 1.
图8
图9
图9
基于逻辑回归的预测模型ROC曲线
Fig.9
Receiver operation characteristic curve based on logistic regression
2.2.4 基于GBDT的直肠癌T分期模型预测
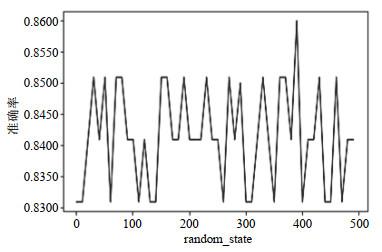
使用sklearn工具包中的GradientBoostingClassifier类来构建模型,GBDT是用损失函数的负梯度来拟合本轮损失的近似值,进而拟合成一个CART回归树,对模型影响较大的参数有n_estimators(弱学习器的最大迭代次数)、learning_rate(学习率)、random_state(随机状态等).在建模过程中,本文首先对弱学习器的最大迭代次数以及学习率进行调参.将n_estimators设置在10~100之间,间隔为5,learning_rate取0.01、0.1、0.15、0.2,进行网格搜索得到模型最高准确率为0.840 9,此时n_estimators=25,learning_rate=0.15;然后调整random_state,固定n_estimators=25、learning_rate=0.15,在10~500的范围内以10为步长分别建模,并绘制GBDT学习曲线(图 10).
图10
在random_state=400时,模型准确率达到最高,为0.860 0.因此设置GradientBoostingClassifier类的参数n_estimators=25、learning_rate=0.15、random_state=400构建模型,绘制ROC曲线(图 11).模型的十折交叉验证后的平均AUC、准确率、灵敏度、特异度为0.856 8、0.860 0、0.925 0、0.896 0,测试集准确率达到了0.809 5.
图11
图11
基于GBDT的预测模型的ROC曲线
Fig.11
Receiver operation characteristic curve of the prediction model based on GBDT
2.2.5 各模型判别效果比较
本研究基于影像组学的方法,对直肠癌患者的术前T分期进行了预测.通过在T2WI影像上对肿瘤进行勾画并提取特征,使用LASSO算法选择了7个与T分期最相关的影像组学特征,其中包含6个形状特征和1个纹理特征.使用了逻辑回归、SVM、GBDT、随机森林四种算法对其建模,其中SVM是效果最优的算法,其AUC、准确率、灵敏度、特异度均高于其他四种算法,AUC更是达到了0.968 5(表 2),高于王进等[26]使用SVM算法预测T分期的AUC(0.768),以及Dou等[11]使用基于LASSO的逻辑回归算法的预测AUC均值0.85,其原因在于本文使用了多种模型进行比较,并对每个模型进行了细致的调参处理,使模型的准确率达到了较高的水平.该模型在测试集上的准确率为0.904 7,在临床诊断中,可以为医生提供可靠的参考.同时,经LASSO算法选择后的特征在四个模型中均有良好表现:AUC值均达到0.85以上,准确率也都高于0.83,正如Lambin等[27]提到的,好的影像组学特征在不同分类器上都应该有较好的效果.
表2 4个模型预测各项指标值
Table 2
| 模型 | AUC | 准确率 | 灵敏度 | 特异度 | 测试集准确率 |
| 随机森林 | 0.9015 | 0.8300 | 0.9107 | 0.8690 | 0.8571 |
| 支持向量机 | 0.9685 | 0.8864 | 0.9625 | 0.8992 | 0.9047 |
| 逻辑回归 | 0.9439 | 0.8476 | 0.9057 | 0.8894 | 0.8571 |
| GBDT | 0.8568 | 0.8600 | 0.9250 | 0.8960 | 0.8095 |
3 结论与展望
本文基于影像组学对直肠癌术前T分期预测进行了研究,首先在放射科医生勾画好的ROI区域上使用pyradiomics工具包提取特征,使用LASSO算法选择了与T分期高度相关的7个影像组学特征,使用随机森林、SVM、逻辑回归、GBDT四种算法分别对特征进行建模,其中SVM算法表现最优,AUC、准确率、灵敏度、特异度为0.968 5、0.886 4、0.962 5、0.899 2,测试集准确率0.904 7,大幅提高了直肠癌T分期的准确率;同时,本文对各个模型都进行了细致的调参处理,以达到提高分类准确率的目的.在未来的工作中,可以从模型融合和多模态数据角度出发,开发更优的预测模型.
参考文献
Global, regional, and national cancer incidence, mortality, years of life lost, years lived with disability, and disability-adjusted life-years for 29 cancer groups, 1990 to 2016:a systematic analysis for the global burden of disease study
[J].
The rising incidence of younger patients with colorectal cancer: questions about screening, biology, and treatment
[J].
The impact of the rising colorectal cancer incidence in young adults on the optimal age to start screening: Microsimulation analysis I to inform the American Cancer Society colorectal cancer screening guideline
[J].
2015年中国恶性肿瘤流行情况分析
[J].DOI:10.3760/cma.j.issn.0253-3766.2019.01.005 [本文引用: 1]
NCCN clinical practice guidelines in oncology: rectal cancer
[J].DOI:10.6004/jnccn.2009.0057 [本文引用: 1]
Radiomics: Extracting more information from medical images using advanced feature analysis
[J].DOI:10.1016/j.ejca.2011.11.036 [本文引用: 2]
MRI与CT在直肠癌诊断及术前分期中价值探究
[J].DOI:10.3969/j.issn.2096-3807.2018.24.092 [本文引用: 1]
The accuracy of MRI in preoperative T staging diagnosis of rectal cancer
[J].DOI:10.3877/cma.j.issn.2095-3224.2014.05.09 [本文引用: 1]
术前应用MRI评估直肠癌T分期的价值
[J].DOI:10.3877/cma.j.issn.2095-3224.2014.05.09 [本文引用: 1]
The development and validation of a CT-based radiomics signature for the preoperative discrimination of stage Ⅰ-Ⅱ and stage Ⅲ-Ⅳ colorectal cancer
[J].DOI:10.18632/oncotarget.8919 [本文引用: 1]
T stage prediction of colorectal tumor based on multiparametric functional images
[J].DOI:10.21037/tcr.2019.11.41 [本文引用: 2]
Rectal cancer: Toward fully automatic discrimination of T2 and T3 rectal cancers using deep convolutional neural network
[J].DOI:10.1002/ima.22311 [本文引用: 1]
A predictive nomogram for individualized recurrence stratification of bladder cancer using multiparametric MRI and clinical risk factors
[J].DOI:10.1002/jmri.26749 [本文引用: 1]
User-guided 3D active contour segmentation of anatomical structures: Significantly improved efficiency and reliability
[J].DOI:10.1016/j.neuroimage.2006.01.015 [本文引用: 1]
Random forest
[J].DOI:10.1023/A:1010933404324 [本文引用: 1]
Classification and regression by randomforest
[J].
Computational radiomics system to decode the radiographic phenotype
[J].DOI:10.1158/0008-5472.CAN-17-0339 [本文引用: 1]
Identifying interacting SNPs using Monte Carlo logic regression
[J].
Support vector machine
[J].
Least squares support vector machine classifiers: an empirical evaluation
[J].
Greedy function approximation: A gradient boosting machine
[J].DOI:10.1214/aos/1013203450 [本文引用: 1]
Stochastic gradient boosting
[J].
Scikit-learn: machine learning in python
[J].
The value of high resolution T2WI-based radiomics in the preoperative staging of rectal cancer
[J].
基于高分辨T2WI的影像组学对直肠癌术前分期的应用价值
[J].
Radiomics: the bridge between medical imaging and personalized medicine
[J].DOI:10.1038/nrclinonc.2017.141 [本文引用: 1]