
摘要: Nechtschein等人报道并分析了反式聚乙炔中质子自旋晶格弛豫时间对拉摩频率ω和温度T的依赖关系。观察到了质子自旋晶格弛豫速率T1-1和ω-1/2的正比关系。但是在高频段,T1-1∝ω-1/2关系发生偏离,且温度越低,发生偏离的频率也越低。
本文用另一种方法对这些实验结果作了分析。首先,论证了孤子一维扩散模型的合理性。排除了质子弛豫速率∝ω-1/2的另一种解释,即仅仅是核自旋向着静止的顺磁中心扩散。孤子能处在运动状态或静止状态。当温度降低时,发生两个效应,即越来越少的孤子处于运动状态,且运动孤子的扩散系数减小。只有扩散的孤子对所观察到的质子弛豫有贡献,而固定孤子的贡献可以忽略。其次,描述了运动孤子的一维随机行走模型,计算了它的相关函数和谱密度函数。质子自旋晶格弛豫速率是: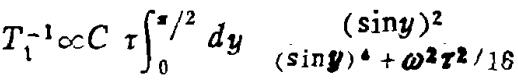
其中C是运动孤子的浓度,τ是运动孤子沿链跳跃时,渡越相邻位置的跳跃时间,ω是质子的拉摩频率。
这个公式揭示了质子弛豫速率的频率和温度依赖关系的主要特征。它和Nechtschein的测量结果拟合得很好。从拟合中可以得到各个温度下运动孤子的跳跃时间和相对浓度。