1 引言
作为一种新兴的控制技术, 迭代学习控制起源于机器人应用[7], 考虑的是寻求控制力矩, 通过循环反复利用前一轮得到的信息来改进本轮的信息, 使得机器人于有限时间区间段内按照设定的轨迹运动. 因这类控制方法在具有固定控制目标的循环重复系统上的适用性, 以及对未知模型系统的控制方面有着独到的优势, 吸引了众多学者将其应用到偏微分系统的控制问题中[8-11]. 文献[8]基于
近年来, 多智能体系统的协调控制是控制领域中的一个热点研究课题, 其主要涉及到无领航者系统的一致性控制、含一个领航者系统的跟踪控制, 以及含多个领航者系统的包容控制等. 一致性控制考虑的是如何使每个智能体的状态(或输出)能够随着时间的增长而趋于同一个值[12-13]; 跟踪控制考虑的是如何使每个跟随者的状态(或输出)能够随时间的增长而趋于同一个领航者的状态(或输出)[14-18]; 包容控制考虑的则是如何使每个跟随者的状态(或输出)能够随时间增长而趋于由多个领航者的状态(或输出)构建的凸包内[19-23]. 上述基于Lyapunov稳定性意义的研究成果涉及的均为常微分多智能体系统. 最近, 有关偏微分多智能体系统的协调控制问题引起了人们的关注[24-25]. 文献[24]提出并研究了一类二阶抛物型或双曲型偏微分多智能体系统的一致性控制问题, 采用Lyapunov泛函方法, 构建得到反馈控制协议, 证明了系统的一致性误差随时间趋于无穷时于
最近, 文献[29]首次将迭代学习算法应用到多智能体系统的包容控制问题中, 并针对一类异构的非线性常微分多智能体系统, 构建得到基于包容性的分布式迭代学习控制律, 证明了当迭代次数趋于无穷时, 系统的包容误差能够在有限时间区间内收敛于零. 这激发了本文的研究工作.
符号约定: 对于函数
其中
2 预备知识与问题描述
用有向图
设含有多个领航者的多智能体系统是由
记信息交换矩阵
假设2.1[19] 对于每个跟随者, 至少存在一条由某个领航者出发且连结它的通路.
当假设2.1成立时, 有下列引理.
引理2.1[19] 矩阵
设由
含有迭代和控制变量的
其中,
不含迭代和控制变量的
其中,
假设2.2[26] 对所有的
(或
(或
基于迭代学习的包容控制的目标是: 构建
其中的常数
记
则系统(2.1)可以写成如下的紧凑形式
记
定义一个新变量
3 主要结果
对于系统(2.3), 构建如下形式的
其中
根据包容误差
这里
应用Cauchy-Schwarz积分不等式, 有
将上式代入(3.3)式, 可得
取
另一方面, 结合系统(2.3)和(3.1)式, 可知
3.1 抛物型多智能体系统的包容控制$ (\gamma = 1) $
定理3.1 假设2.1、2.2成立, 且(3.2)式成立, 则在迭代学习律(3.1)的作用下, 随着迭代次数
证 (3.5)式两端左乘
而
分部积分并结合假设2.2中的边值定位条件, 可知
将(3.7)–(3.9)式代入到(3.6)式, 可推得
应用Gronwall引理, 并结合假设2.2中的初值定位条件, 有
由此
进一步有
将(3.10)–(3.11)式代入到(3.4)式, 可得
这里
由(3.2)式可知,
从而
由此可知, 当迭代次数
3.2 双曲型多智能体系统的包容控制($ \gamma = 2 $
定理3.2 假设2.1、2.2成立, 且(3.2)式成立, 则在迭代学习律(3.1)的作用下, 随着迭代次数
证 (3.5)式两端左乘
而
分部积分并结合假设2.2中的边值定位条件, 可知
将(3.13)–(3.15)式代入(3.12)式, 可推得
应用Gronwall引理, 并结合假设2.2中的初值定位条件, 有
由此
另一方面, 应用基本不等式, 有
应用Gronwall引理, 并结合假设2.2中的初值定位条件, 可推得
取
将(3.16)式代入(3.17)式得
进一步有
将(3.18)–(3.19)式代入(3.4)式, 可得
这里
由(3.2)式可知,
从而
由此可知, 当迭代次数
注3.1 当
4 仿真算例
对系统(2.1)、(2.2), 取
2个领航者的动态模型为
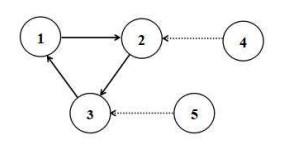
设多智能体系统的通讯拓扑如图 1所示, 显然, 假设2.1成立.
图 1
相应的Laplacian矩阵为
因此
从而, 包容误差表示为
取
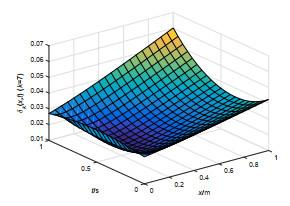
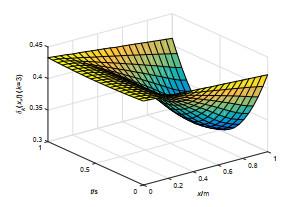
图 2
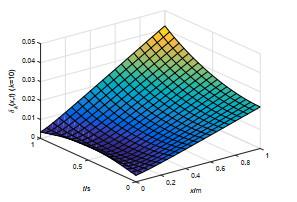
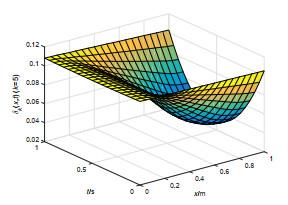
图 3
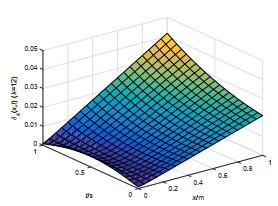
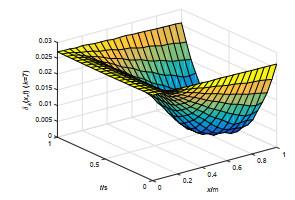
图 4
图 5
图 5
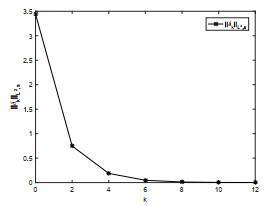
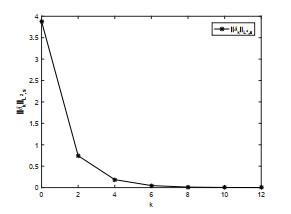
抛物型包容误差
图 6
图 7
图 8
图 9
图 9
双曲型包容误差
5 结论
参考文献
Feature learning via partial differential equation with applications to face recognition
DOI:10.1016/j.patcog.2017.03.034 [本文引用: 1]
A nonlinear approximation method for solving high dimensional partial differential equations: Application in finance
DOI:10.1016/j.matcom.2016.07.013 [本文引用: 1]
Application of hyperbolic partial differential equations in global optimal scheduling of UAV
DOI:10.1016/j.aej.2020.02.013 [本文引用: 1]
柔性机器人的动力学建模及控制
Dynamic modeling and control of flexible robotic manipulators
Bettering operation of robots by learning
DOI:10.1002/rob.4620010203 [本文引用: 1]
Closed-loop P-type iterative learning control of uncertain linear distributed parameter systems
DOI:10.1109/JAS.2014.7004684 [本文引用: 2]
非正则分布参数系统的迭代学习控制
Iterative learning control for irregular distributed parameter systems
A PD-type iterative learning control algorithm for one-dimension linear wave equation
DOI:10.1007/s12555-019-0094-5 [本文引用: 2]
Iterative learning control for one-dimensional fourth order distributed parameter systems
DOI:10.1007/s11432-015-1031-6 [本文引用: 3]
Leaderless consensus control of uncertain multi-agent systems with sensor and actuator attacks
DOI:10.1016/j.ins.2019.07.075 [本文引用: 1]
Event-triggered consensus control of disturbed multi-agent systems using output feedback
DOI:10.1016/j.isatra.2019.02.004 [本文引用: 1]
${H_∞}$ Consensus for linear heterogenerous multi-agent systems with state and output feedback
Distributed adaptive event-triggered protocol for tracking control of leader-following multi-agent systems
DOI:10.1016/j.jfranklin.2018.07.019
Distributed estimation and control for nonlinear multi-agent systems in the presence of input delay or external disturbances
DOI:10.1016/j.isatra.2019.08.059
Observer-based adaptive consensus control for nonlinear multi-agent systems with time-delay
Event-triggered leader-following consensus of non-linear multi-agent systems with switched dynamics
DOI:10.1049/iet-cta.2018.5126 [本文引用: 1]
Output containment control for swarm systems with general linear dynamics: A dynamic output feedback approach
DOI:10.1016/j.sysconle.2014.06.007 [本文引用: 4]
Containment control of linear multi-agent systems with directed graphs and multiple leaders of time-varying bounded inputs
Event-triggered distributed containment control of heterogeneous linear multi-agent systems by an output regulation approach
DOI:10.1080/00207721.2017.1309595
Event-triggered containment control of second-order nonlinear multi-agent systems
DOI:10.1016/j.jfranklin.2018.05.060
Finite-time containment control for nonlinear multi-agent systems with external disturbances
DOI:10.1016/j.ins.2019.05.049 [本文引用: 1]
Consensus control for multi-agent systems with distributed parameter models
Containment control for partial differerntial multi-agent systems
Consensus control for multi-agent systems with distributed parameter models via iterative learning algorithm
Consensus control via iterative learning for distributed parameter models multi-agent systems with time-delay
四阶偏微分多智能体系统的迭代学习控制
DOI:10.3969/j.issn.1003-3998.2020.04.018 [本文引用: 3]
Iterative learning control for fourth order partial differential multi-agent systems
DOI:10.3969/j.issn.1003-3998.2020.04.018 [本文引用: 3]
Iterative learning control for nonlinear heterogeneous multi-agent systems with multiple leaders
DOI:10.1177/0142331220941636 [本文引用: 2]
D-type anticipatory iterative learning control for a class of inhomogeneous heat equations
DOI:10.1016/j.automatica.2013.05.005 [本文引用: 1]