害虫爆发往往造成严重的生态破坏和经济损失,因此在过去的二十年里如何有效地控制害虫和其他节肢动物已经成为一个越来越复杂的问题.因为化学杀虫剂可以迅速杀死大量的害虫防止经济损失,所以被人类大量使用来降低害虫的数目.但长时间的滥用农药会引起一系列的问题如使害虫产生抗药性,非目标生物(如害虫天敌)被大量捕杀,在农作物和生态系统中会有化学残留^[1-2].由于这些原因,补充或替代的生物防治方法被建议投入使用^[3-8].特别地,释放害虫病原体是通过在生态系统引入害虫病原体,包括细菌、真菌、病毒、线虫和原生动物,旨在减少易感害虫数量的一种生物防治方法.这些害虫病原体会使节肢动物感染疾病,尤其昆虫和螨^[9-17].它们的作用是在害虫种群中产生一种流行病从而使易感害虫的数量减少,最终达到保护农作物的目的.

目前,害虫病原体在害虫防治中的应用及其数学建模已经吸引了许多学者的关注^[18-26]. Meng等^[18]考虑了在农业生态系统中如果害虫数量(易感)达到经济阈值ET,则通过脉冲捕获(易感个体)和脉冲释放(感染个体)进行害虫控制的综合害虫治理问题. Ding等^[19]建立了具有时间延迟和阶段结构的$SI$传染病模型,并且分析了两个阈值对病虫释放量变化的敏感性. Tang等^[21]建立了具有传染病的害虫-天敌相互作用的害虫综合治理模型,分析了喷洒杀虫剂和释放天敌,病虫的不同使用频率对阈值的影响.然而,一方面他们考虑的大多是无限时间的脉冲控制模型.而在我们的实际生活中,有时不需要使易感害虫灭绝,这是因为田间适当数量的害虫对于保护天敌,以及维持农作物的经济补偿是有益的.另一方面他们很少研究综合害虫治理问题中脉冲干预的最佳时刻和强度.

综合害虫管理策略(IPM)的核心对于确定控制策略是有效的: (1)减少害虫数量使其低于经济阈值; (2)确保对环境的破坏最小; (3)确保这些策略在经济上可行^[3].在本文中我们提出了通过最优选择脉冲干预的时刻和强度从而使终端观测时刻易感害虫的数量,以及喷洒杀虫剂和释放病虫的总成本达到最小的多个脉冲控制策略.现如今,脉冲系统的最优控制理论,分析和数值技术已经得到很好的发展^{[14, 27-33]}.例如,文献[27]通过分析目标函数的可微性,计算了目标函数关于控制变量的梯度.基于时间尺度变换的方法被广泛地用来优化脉冲时刻^[29-31],并且Loxton等严格说明了这种方法的优点^[32].在本文中,我们借助时间缩放和时间平移的方法计算了目标函数关于控制变量的梯度从而获得了最小的目标函数.

本文的其余部分如下.第二节描述了通过最优选择控制参数从而使目标函数达到最小的一类最优脉冲控制问题.第三节建立了一个具有喷洒杀虫剂和释放有病害虫的脉冲控制的害虫治理$SI$模型,并且提出了使易感害虫彻底灭绝的策略.在第四节,通过梯度计算,三个基于不同脉冲干预频率和强度的有限时间的最优控制策略被提出.第五节基于数值模拟提出了最有效的害虫管理控制策略.最后,第六节给出了讨论.

考虑脉冲方程

(2.1) $ \begin{equation}\label{g1}\left\{ \begin{array}{ll} \left.\begin{array}{ll} \frac{{\rm d}\tilde{S}(t)}{{\rm d}t}=P(t, \tilde{S}(t), \tilde{I}(t)), \\ \frac{{\rm d}\tilde{I}(t)}{{\rm d}t}=R(t, \tilde{S}(t), \tilde{I}(t)), \end{array}\right\}t\neq \tilde{t}_j, ~~t\neq t_i, \\ \left.\begin{array}{ll} \tilde{S}(\tilde{t}_j^+)=\varrho_j^1(\tilde{S}(\tilde{t}_j), \tilde{I}(\tilde{t}_j), \alpha_j), \\ \tilde{I}(\tilde{t}_j^+)=\varrho_j^2(\tilde{S}(\tilde{t}_j), \tilde{I}(\tilde{t}_j), \alpha_j), \end{array}\right\} t=\tilde{t}_j, ~~j=1, \cdots , m-1, \\ \left.\begin{array}{ll} \tilde{S}(t_i^+)=o_i^1(\tilde{S}(t_i), \tilde{I}(t_i), \beta_i), \\ \tilde{I}(t_i^+)=o_i^2(\tilde{S}(t_i), \tilde{I}(t_i), \beta_i), \end{array}\right\}t=t_i, ~~i=1, \cdots , n-1, \end{array}\right. \end{equation} $

初始条件为

(2.2)$\begin{equation}\label{g2} \tilde{S}(0)=\tilde{S}^{0}, ~~~~\tilde{I}(0)=\tilde{I}^{0}, \end{equation} $

其中$\varrho_j^h$和$o_i^h, ~h=1, 2, $表示在时刻$\tilde{t}_j$和$t_i$进行脉冲干预后种群$\tilde{S}$和$\tilde{I}$的数量; $\alpha_j$和$\beta_i$表示系统参数; $m>1, ~n>1$表示脉冲干预次数.

不失一般性,假设跳跃时刻和系统参数的边界约束如下:

(H1) $ 0\leqslant \tilde{t}_1\leqslant\cdots \leqslant \tilde{t}_m=t_f$且$ 0\leqslant t_1\leqslant\cdots \leqslant t_n=t_f. $

(H2) $ \alpha^1_j\leqslant \alpha_j\leqslant \alpha^2_j, ~j=1, \cdots, m-1, $且$\beta^1_i\leqslant \beta_i\leqslant \beta^2_i, ~i=1, \cdots, n-1, $其中$\alpha^h_j, ~\beta^h_i, ~h=1, 2, $是给定的常数,满足$0<\alpha^1_j<\alpha^2_j, ~ 0<\beta^1_i<\beta^2_i.$

为方便讨论,令${\mathit{\boldsymbol{\zeta }}} =\left(\tilde{t}_1, \cdots, \tilde{t}_{m-1}, t_1 \cdots, t_{n-1}\right)^T$, ${\mathit{\boldsymbol{\beta }}}=\left(\alpha_1, \cdots, \alpha_{m-1}, \beta_1, \cdots, \beta_{n-1}\right)^T.$用$\Upsilon$和$\Psi$表示严格满足(H1)和(H2)的${\mathit{\boldsymbol{\zeta }}}\in {\mathbb{R}}^{m+n-2}$和${\mathit{\boldsymbol{\beta }}}\in {\mathbb{R}}^{m+n-2}$的集合.进一步,定义

${\mathit{\boldsymbol{\hbar }}}=\left(\tilde{S}(t), \tilde{I}(t)\right)^{\tiny T}, ~~~~{\mathit{\boldsymbol{\wp }}}_0=\left(\frac{{\rm d}\tilde{S}(t)}{{\rm d}t}, \frac{{\rm d}\tilde{I}(t)}{{\rm d}t}\right)^{\tiny T}, $

$ ~ {\mathit{\boldsymbol{\wp }}}_j= \left(\tilde{S}\left(\tilde{t}_j^+\right), \tilde{I}\left(\tilde{t}_j^+\right)\right)^{\tiny T}, ~ {\mathit{\boldsymbol{\wp }}}_i= \left(\tilde{S}\left(t_i^+\right), \tilde{I}\left(t_i^+\right)\right)^{\tiny T}.$

(H3)给定的函数${\mathit{\boldsymbol{\wp }}}_0$, ${\mathit{\boldsymbol{\wp }}}_j$和${\mathit{\boldsymbol{\wp }}}_i$,关于它们所有的参数是连续可微的.

(H4)存在实数$\ell$使

$\left\|{\mathit{\boldsymbol{\wp }}}_0({\mathit{\boldsymbol{\hbar }}})\right\|\leqslant \ell\left(1+\left\|{\mathit{\boldsymbol{\hbar }}}\right\|\right), $

其中$\|\cdot\|$表示欧几里得范数.

假设(H3)和(H4)保证了对任意的$({\mathit{\boldsymbol{\zeta }}}, {\mathit{\boldsymbol{\beta }}})\in \left(\Upsilon, \Psi\right)$,脉冲系统(2.1)在初始条件(2.2)下的解${\mathit{\boldsymbol{\hbar }}}(\cdot|{\mathit{\boldsymbol{\zeta }}}, {\mathit{\boldsymbol{\beta }}})$是唯一的.

定义目标函数

(2.3)$ \begin{equation}\label{cost1}J({\mathit{\boldsymbol{\zeta }}}, {\mathit{\boldsymbol{\beta }}})=\Phi(\tilde{S}(t_f), \tilde{I}(t_f), {\mathit{\boldsymbol{\zeta }}}, {\mathit{\boldsymbol{\beta }}}), \end{equation} $

其中函数$\Phi: {\mathbb{R}}\times {\mathbb{R}}\times {\mathbb{R}}^{m+n-2}\times {\mathbb{R}}^{m+n-2}\rightarrow {\mathbb{R}} $连续可微.接下来,我们描述标准的最优控制问题.

问题(P)  通过最优选择控制参数$({\mathit{\boldsymbol{\zeta }}}, {\mathit{\boldsymbol{\beta }}})\in \left(\Upsilon, \Psi\right)$使满足(2.1)和(2.2)式的目标函数(2.3)达到最小.

在本节中,我们描述了一类脉冲时间点和系统参数均不确定的优化控制问题.假设(H1)-(H4)保证了我们提出的优化问题优化解的存在性.接下来,我们将基于一个具有流行病的害虫管理模型的优化控制问题,用时间尺度变化和时间平移技巧,给出优化算法.

本文的研究基于如下具有易感害虫$S$和染病害虫$I$的IPM模型

(3.1)$\begin{equation}\label{sec1-1} \left\{\begin{array}{ll} \frac{{\rm d}S}{{\rm d}t}=rS(t)\left(1-\frac{S(t)+\theta I(t)}{K}\right)-\frac{\beta S(t)I(t)}{1+aS(t)}, \\ \frac{{\rm d}I}{{\rm d}t}=\frac{\lambda\beta S(t)I(t)}{1+aS(t)}-wI(t). \\ \end{array}\right.\end{equation}$

该模型依赖如下生物假设:

(A1)易感害虫遵循内禀增长率为$r$,环境容纳量为$K$的logistic增长.

(A2)虽然染病害虫没有生育能力,但和$S$一样对资源和环境具有竞争力.

(A3) ${\beta S(t)}/{(1+aS(t))}$表示饱和传染率,其中$a$表示半饱和系数, $\beta$表示接触率.

(A4)参数$\lambda$表示从易感害虫到病虫的转换率.

(A5)参数$w$表示染病害虫$I$的自然死亡率.

在实际生活中,为了在一个特定的时间内消除害虫或者有效地控制农作物害虫的数量,必须施加人为干预.一般来说,人类进行害虫管理的行为非连续.为此,研究以下带有脉冲喷洒农药和释放有病害虫的$SI$数学模型.

在脉冲时间点$t=i\tau, ~i=1, 2, \cdots $,施加脉冲干预后,模型(3.1)被修改如下

(3.2) $ \begin{equation}\label{sec1-2} \left\{\begin{array}{ll} \left.\begin{array}{ll} \frac{{\rm d}S}{{\rm d}t}=rS(t)\left(1-\frac{S(t)+\theta I(t)}{K}\right)-\frac{\beta S(t)I(t)}{1+aS(t)}, \\ \frac{{\rm d}I}{{\rm d}t}=\frac{\lambda\beta S(t)I(t)}{1+a S(t)}-w I(t), \end{array}\right\}t\neq i\tau, \\ \left.\begin{array}{ll} S(t^{+})=(1-\mu)S(t), \\ I(t^{+})=(1-\sigma\mu)I(t)+\delta, \end{array}\right\}t= i\tau, ~i=1, 2, \cdots , ~~i\in Z_+. \\ \end{array}\right.\end{equation} $

(A6)参数$0\leqslant\mu<1 $和$\sigma\mu$($0\leqslant\sigma\leqslant 1$)分别表示由于喷洒杀虫剂使易感害虫和染病害虫减少的比例.

(A7) $\delta$表示有病害虫的释放量, $\tau$表示脉冲周期.

因为治理土壤和森林中的害虫是一个长期的行为,所以我们将努力抑制和消除易感害虫,这意味着易感个体永远不存在于害虫种群.因此,通过文献[1,定理4.2],以下结果说明了为消除易感害虫所施加的脉冲干预的强度.

定理3.1  如果

(3.3)$ \begin{equation}\label{sec1-3} r\tau-\frac{\delta \left(r\theta+\beta K\right)\left(1-\exp(-w\tau)\right)}{wK[1-(1-\sigma\mu)\exp(-w\tau)]}<\ln\frac{1}{1-\mu}, \end{equation}$

则模型(3.2)的易感害虫灭绝周期解$(0, I^*(t))$是全局渐近稳定的,其中

$I^*(t)=\frac{\delta\exp(-w(t-i\tau))}{1-(1-\sigma\mu)\exp(-w\tau)}, ~t\in(i\tau, (i+1)\tau], ~i\in Z_+.$

推论3.1  易感害虫灭绝周期解$(0, I^*(t))$是全局渐近稳定的,假设下列条件之一成立

(3.4)$\begin{equation}\label{sec1-4} \delta>\frac{wK[r\tau+\ln(1-\mu)][1-(1-\sigma\mu)\exp(-w\tau)]}{(r\theta+\beta K)(1-\exp(-w\tau))}\doteq\hat{\delta}, \end{equation}$

(3.5)$\begin{equation}\label{sec1-5}\mu>1-\exp\left\{-r\tau+\frac{\delta \left(r\theta+\beta K\right)\left(1-\exp(-w\tau)\right)}{wK[1-(1-\sigma\mu)\exp(-w\tau)]}\right\}\doteq \hat{\mu}, \end{equation}$

(3.6)$ \begin{equation}\label{sec1-6}\tau<\hat{\tau}, \end{equation}$

其中, $\hat{\tau}$是

$f(\tau)=r\tau-\frac{\delta \left(r\theta+\beta K\right)\left(1-\exp(-w\tau)\right)}{wK[1-(1-\sigma\mu)\exp(-w\tau)]}+\ln(1-\mu)$

的零根.

由推论3.1得,如果脉冲周期$\tau$小于阈值$\hat{\tau}$,或者病虫的释放量$\delta$大于阈值$\hat{\delta}$,或者由于喷洒杀虫剂导致的易感害虫的死亡率$\mu$大于阈值$\hat{\mu}$,那么易感害虫会灭绝.事实上,这样的策略在生态上并不可取.一方面是它会造成害虫的再次爆发.另一方面,释放的病虫会使害虫种群的数量增加并且消耗农作物.又因为许多农作物的生长周期有限,而且适当数量的害虫对于保护天敌,以及维持农作物的经济补偿是有益的,所以可以通过优化病虫的释放量和农药的喷洒量使害虫的数目被控制在经济危害水平之下.因此为了控制易感害虫使其在一定的时间内不会造成经济损失,我们需要寻找最优的脉冲控制策略.

在下面,我们将考虑三种害虫防治策略:非固定时刻的变量综合控制,非固定时刻的交替综合控制,以及固定时刻的不变综合控制.最终,基于梯度技术,利用时间尺度变换和时间平移变换的方法可以把这些问题转化为等价的最优参数选择问题.

因为在实际生活中,农民常常根据农作物的生长周期和害虫的生长发育调整控制策略^[34],所以在本小节中,我们将模型(3.2)构建为最一般的形式

(4.1)$\begin{equation}\label{sec3-30}\left\{ \begin{array}{ll} \left.\begin{array}{ll} \frac{{\rm d}S}{{\rm d}t}=rS(t)\left(1-\frac{S(t)+\theta I(t)}{K}\right)-\frac{\beta S(t)I(t)}{1+aS(t)}, \\ \frac{{\rm d}I}{{\rm d}t}=\frac{\lambda\beta S(t)I(t)}{1+aS(t)}-wI(t), \end{array}\right\} t\neq t_i, \\ \left.\begin{array}{ll} S(t_i^{+})=(1-\mu_i)S(t_i), \\ I(t_i^{+})=(1-\sigma\mu_i)I(t_i)+\delta_i, \end{array}\right\}t=t_i, ~i=1, \cdots , N-1, \\ \end{array}\right.\end{equation}$

初始条件

(4.2)$\begin{equation}\label{sec3-2}S(0)=S^{0}, ~~~~~I(0)=I^{0}.\end{equation}$

假设下列条件满足

(4.3)$ \begin{equation}\label{sec3-3} \mu_i^1\leqslant\mu_i\leqslant \mu_i^2, ~~~~\delta_i^1\leqslant\delta_i\leqslant \delta_i^2, \end{equation}$

(4.4) $ \begin{equation}\label{sec3-4} 0=t_0\leqslant t_1\leqslant \cdots \leqslant t_{N}=t_f, \end{equation} $

其中$t_f$表示终端观测时刻, $\mu_i^1, ~\mu_i^2, ~\delta_i^1$和$\delta_i^2$是给定的非负常数.

为了简便,令

${\mathit{\boldsymbol{\mu }}}=(\mu_1, \cdots , \mu_{N-1})^{T}, {\mathit{\boldsymbol{\delta }}}=(\delta_1, \cdots , \delta_{N-1})^{T}, {\mathit{\boldsymbol{\zeta }}}=(t_1, \cdots, t_{N-1})^{T}.$

现在我们正式地描述最优害虫控制问题:给定满足初始条件(4.2)的动力系统(4.1),寻找最优控制参数${\mathit{\boldsymbol{\zeta }}}, ~{\mathit{\boldsymbol{\mu }}}, ~{\mathit{\boldsymbol{\delta }}} $使目标函数

(4.5)$ \begin{equation}\label{sec3-31}J({\mathit{\boldsymbol{\zeta }}}, {\mathit{\boldsymbol{\mu }}}, {\mathit{\boldsymbol{\delta }}})=S(t_f)+\sum\limits_{i=1}^{N-1}(P_1\mu_i+P_2\delta_i) \end{equation} $

达到最小,其中$P_1>0, ~P_2>0$分别表示喷洒农药和释放病虫的成本.称此为问题(PA).

因为状态$S$和$I$依赖跳跃时刻,所以不能利用现有的技术直接求解问题(PA).然而,基于梯度技术,利用时间尺度变换和时间平移变换的方法该问题被转化为一个等价的最优参数选择问题,困难就能迎刃而解.

首先,时间尺度变换将变化的脉冲时间点$0=t_0, t_1, \cdots, t_{N-1}, t_{N}=t_f$映射在一个新的时间尺度$s=0, 1, \cdots, N$上.

定义所需变换的微分方程如下

(4.6)$ \begin{equation}\label{sec3-6} \frac{{\rm d}t(s)}{{\rm d}s}=v(s), \end{equation}$

初始条件为

(4.7)$\begin{equation}\label{sec3-7}t(0)=0, \end{equation} $

其中$v(s)$表示时间缩放控制函数,它是一个分段常数函数,在$s=1, 2, \cdots, N-1$上有可能的不连续点,即

(4.8)$\begin{equation}\label{sec3-8}v(s)=\sum\limits_{i=1}^{N}\tau_i\chi_{(i-1, i)}(s), \end{equation} $

其中$\tau_i=t_{i}-t_{i-1}, ~i=1, \cdots, N, $满足

(4.9)$\begin{equation}\label{sec3-9}\sum\limits_{i=1}^{N}\tau_i= t_f, \end{equation}$

且$\chi_{D}(s)$为指示函数,被定义为

(4.10)$\begin{equation}\label{sec3-10} \chi_{D}(s) =\left\{\begin{array}{ll} 1, & \mbox{若} s\in D, \\ 0, & \mbox{其他}. \end{array}\right.\end{equation}$

通过时间缩放变换,问题(PA)的系统动力学改变为

(4.11)$\begin{equation}\label{sec3-11}\left\{\begin{array}{ll} \left.\begin{array}{ll} \frac{{\rm d}S}{{\rm d}s}=v(s)\left\{rS(s)\left(1-\frac{S(s)+\theta I(s)}{K}\right)-\frac{\beta S(s)I(s)}{1+aS(s)}\right\}, \\ \frac{{\rm d}I}{{\rm d}s}=v(s)\left\{\frac{\lambda\beta S(s)I(s)}{1+aS(s)}-wI(s)\right\}, \end{array}\right\}s\in(0, N], \\ \left.\begin{array}{ll} S(i^{+})=(1-\mu_i)S(i), \\ I(i^{+})=(1-\sigma\mu_i)I(i)+\delta_i, \end{array}\right\}i=1, \cdots , N-1, \\ \end{array}\right.\end{equation}$

具有初始条件(4.2).

因此,问题(PA)转变为:通过最优选择${\mathit{\boldsymbol{\zeta }}}, ~{\mathit{\boldsymbol{\mu }}}, ~{\mathit{\boldsymbol{\delta }}}$,使转换后的目标函数

(4.12)$ \begin{equation}\label{sec3-12}J({\mathit{\boldsymbol{\zeta }}}, {\mathit{\boldsymbol{\mu }}}, {\mathit{\boldsymbol{\delta }}})=S(N)+\sum\limits_{i=1}^{N-1}(P_1\mu_i+P_2\delta_i), \end{equation}$

实现最小,该目标函数满足具有初始条件(4.7), (4.2)的动力学方程(4.6)和(4.11).称此为问题(PB).

然而,由于中间跳跃条件的存在问题(PB)仍然难以解决,故时间平移变换被进一步引入.

对$i=1, \cdots, N$,定义

$S_i(s)=S(s+i-1), ~~I_i(s)=I(s+i-1), ~~\pi_i(s)=t(s+i-1).$

通过时间平移变换后,系统(4.11)和(4.6)转变为

(4.13)$\begin{equation}\label{sec3-32}\left\{ \begin{array}{llll} \left. \begin{array}{ll} \frac{{\rm d}S_i}{{\rm d}s}=f^{i}_{1}(s)=\tau_i\left\{ rS_i(s)\left(1-\frac{S_i(s)+\theta I_i(s)}{K}\right)-\frac{\beta S_i(s)I_i(s)}{1+aS_i(s)}\right\}, \\ \frac{{\rm d}I_i}{{\rm d}s}=f^{i}_{2}(s)=\tau_i\left\{\frac{\lambda\beta S_i(s)I_i(s)}{1+aS_i(s)}-wI_i(s)\right\}, \end{array}\right\}s\in(0, 1], \\\left. \begin{array}{ll} S_i(0)=(1-\mu_{i-1})S_{i-1}(1), \\ I_i(0)=(1-\sigma\mu_{i-1})I_{i-1}(1)+\delta_{i-1}, \end{array}\right\}i=2, \cdots , N, \\ ~~ \frac{{\rm d}\pi_i}{{\rm d}s}=\tau_i, ~i=1, \cdots , N, \\ \end{array}\right.\end{equation}$

具有初始条件

(4.14)$\begin{equation}\label{4-14}S_1(0)=S^{0}, ~~~~I_1(0)=I^0, ~~~~\pi_1(0)=0.\end{equation}$

为方便叙述,令${\mathit{\boldsymbol{\tau }}}=(\tau_1, \cdots, \tau_{N}).$

新的等价问题可以被明确地描述为:在满足具有初始条件(4.14)的动力系统(4.13)下,寻找最优的${\mathit{\boldsymbol{\tau }}}, ~{\mathit{\boldsymbol{\mu }}}, ~{\mathit{\boldsymbol{\delta }}}$使目标函数

(4.15)$\begin{equation}\label{sec3-33}J({\mathit{\boldsymbol{\tau }}}, {\mathit{\boldsymbol{\mu }}}, {\mathit{\boldsymbol{\delta }}})=S_{N}(1)+\sum\limits^{N-1}_{i=1}(P_1\mu_{i}+P_2\delta_{i})\end{equation} $

达到最小.称此问题为问题(PC).

根据文献[26,定理4.1],首先定义相应的哈密顿函数$H_i, ~i=1, \cdots, N, $如下

(4.16)$ \begin{equation}\label{sec3-16} H_i(s, S_i(s), I_i(s), {\mathit{\boldsymbol{\lambda }}}^i(s), {\mathit{\boldsymbol{\tau }}}, {\mathit{\boldsymbol{\mu }}}, {\mathit{\boldsymbol{\delta }}}) =\left(\begin{array}{cc} \lambda^{i}_{1}(s), & \lambda^{i}_{2}(s) \end{array}\right)\left(\begin{array}{cc} f^{i}_{1}(s), & f^{i}_{2}(s) \end{array} \right)^{T}, \end{equation}$

其中${\mathit{\boldsymbol{\lambda }}}^{i}(s)$表示相应的协态,由下列辅助脉冲系统决定

(4.17)$\begin{equation}\label{sec3-34}\left\{\begin{array}{llll}\left.\begin{array}{llll} \dot{\lambda}^{i}_{1}(s)=-\tau_i\left\{\lambda^{i}_{1}(s)\left(r-\frac{\left(2S_i+\theta I_i\right)r}{K}-\frac{\beta I_i}{\left(1+aS_i\right)^2}\right)+\lambda^{i}_{2}(s) \frac{\lambda\beta I_i}{\left(1+aS_i\right)^2}\right\}, \\\dot{\lambda}^{i}_{2}(s)=-\tau_i\left\{\lambda^{i}_{1}(s)\left(-\frac{r\theta S_i}{K}-\frac{\beta S_i}{1+aS_i}\right)+\lambda^{i}_{2}(s)\left(\frac{\lambda\beta S_i}{1+aS_i}-w\right)\right\}, \end{array}\right. \\\left.\begin{array}{llll} \lambda^{i}_{1}(1)=\left(1-\mu_i\right)\lambda^{i+1}_{1}(0), \\ \lambda^{i}_{2}(1)=(1-\sigma\mu_i)\lambda^{i+1}_{2}(0), \end{array}\right\}i=1\cdots , N-1, \\ \end{array}\right.\end{equation}$

具有横截条件

(4.18)$\begin{equation}\label{sec3-35}\begin{array}{cc} \lambda^{N}_{1}(1)=1, ~~~~\lambda^{N}_{2}(1)=0.\\ \end{array}\end{equation}$

令${\mathit{\boldsymbol{\theta }}}_i(1)=\big(\begin{array}{cc} S_i(1), \ & I_i(1) \end{array}\big)^{T} $且${\mathit{\boldsymbol{\theta }}}_{i+1}(0)={\mathit{\boldsymbol{\phi }}}_{i}({\mathit{\boldsymbol{\theta }}}_{i}(1), \mu_i, \delta_i), ~i=1, \cdots, N-1.$由(4.13)式得

(4.19) $ \begin{equation}\label{sec3-20} {\mathit{\boldsymbol{\phi }}}_{i}({\mathit{\boldsymbol{\theta }}}_{i}(1), \mu_i, \delta_i) =\left( \begin{array}{cc} (1-\mu_i)S_{i}(1), & (1-\sigma\mu_i)I_{i}(1)+\delta_i \\ \end{array} \right)^{T}.\end{equation} $

经过计算得到目标函数(4.15)关于脉冲时间间隔$\tau_j, ~j=1, \cdots, N, $易感害虫的减少比例$\mu_k, $以及病虫释放量$\delta_k, ~k=1, \cdots, N-1, $的梯度分别为

(4.20)$\begin{eqnarray}\label{sec3-36} \frac{\partial J({\mathit{\boldsymbol{\tau }}}, {\mathit{\boldsymbol{\mu }}}, {\mathit{\boldsymbol{\delta }}})}{\partial \tau_j} &=& \int^{1}_{0}\sum^{N}_{i=1}\frac{\partial H_i(s, S_i(s), I_i(s), {\mathit{\boldsymbol{\lambda }}}^i(s), {\mathit{\boldsymbol{\tau }}}, {\mathit{\boldsymbol{\mu }}}, {\mathit{\boldsymbol{\delta }}})}{\partial \tau_j}{\rm d}s \\ &=& \int^{1}_{0}\left\{\lambda^{j}_{1}(s)\left(rS_j(s)\left(1-\frac{S_j(s)+\theta I_j(s)}{K}\right)-\frac{\beta S_j(s)I_j(s)}{1+aS_j(s)}\right)\right. \\ && \left.+\lambda^{j}_{2}(s)\left(\frac{\lambda\beta S_j(s)I_j(s)}{1+aS_j(s)}-wI_j(s)\right) \right\}{\rm d}s, \end{eqnarray} $

(4.21)$\begin{equation}\label{sec3-37} \frac{\partial J({\mathit{\boldsymbol{\tau }}}, {\mathit{\boldsymbol{\mu }}}, {\mathit{\boldsymbol{\delta }}})}{\partial \mu_k} =P_1+\left({\mathit{\boldsymbol{\lambda }}}^{k+1}(0)\right)^{T}\frac{\partial{\mathit{\boldsymbol{\phi }}}_{k}({\mathit{\boldsymbol{\theta }}}_{k}(1), \mu_k, \delta_k)}{\partial \mu_k} =P_1-S_k(1)\lambda^{k+1}_{1}(0)-\sigma I_k(1)\lambda^{k+1}_{2}(0), \end{equation}$

(4.22) $ \begin{equation}\label{sec3-38} \frac{\partial J({\mathit{\boldsymbol{\tau }}}, {\mathit{\boldsymbol{\mu }}}, {\mathit{\boldsymbol{\delta }}})}{\partial \delta_k} =P_2+\left({\mathit{\boldsymbol{\lambda }}}^{k+1}(0)\right)^{T}\frac{\partial{\mathit{\boldsymbol{\phi }}}_{k}({\mathit{\boldsymbol{\theta }}}_{k}(1), \mu_k, \delta_k)}{\partial \delta_k} =P_2+\lambda^{k+1}_{2}(0). \end{equation} $

在本小节中,我们首先描述了一个在不确定时刻脉冲释放量变化的最优害虫控制问题,然后得到了目标函数关于脉冲时间间隔,由于喷洒杀虫剂导致的易感害虫的减少比例以及病虫释放量的梯度,这些梯度公式对于求解优化问题(4.5)是必要的.在本策略中,生物防治和化学防治在同一时刻被实施,接下来将探索另一种交替的控制.

喷洒杀虫剂是一种常见且有价值的化学控制策略之一,它可以迅速降低害虫的数目,有的时候它是防止经济损失的唯一可行的方法.但其弊端在于造成非目标生物被大量捕杀、对产品和环境产生污染以及可能使害虫产生抗药性,以致害虫变得更加难以治理,甚至可能导致害虫再次爆发,所以从绿色农业和环境保护的角度来说,在病虫害防治过程中应该限制农药的使用量.这里,经过交替地喷洒农药和释放病虫后,模型(4.1)被修改为

(4.23) $ \begin{equation}\label{sec3-1} \left\{\begin{array}{ll}\left.\begin{array}{lll} \frac{{\rm d}S}{{\rm d}t}=rS(t)\left(1-\frac{S(t)+\theta I(t)}{K}\right)-\frac{\beta S(t)I(t)}{1+aS(t)}, \\ \frac{{\rm d}I}{{\rm d}t}=\frac{\lambda\beta S(t)I(t)}{1+aS(t)}-wI(t), \\ \end{array}\right\}t\neq t_i, ~i=1, \cdots , 2n, \\ \left.\begin{array}{ll} S(t^{+})=(1-\mu_i)S(t), \\ I(t^{+})=(1-\sigma\mu_i)I(t), \end{array}\right\}t=t_i, ~i=1, 3, \cdots , 2n-1, \\\left.\begin{array}{ll} S(t^{+})=S(t), \\ I(t^{+})=I(t)+\delta_i, \end{array}\right\}t=t_i, ~i=2, 4, \cdots , 2n, \end{array}\right.\end{equation} $

具有初始条件(4.2).为了方便,令

${\mathit{\boldsymbol{\mu }}}=(\mu_{1}, \mu_{3}, \cdots , \mu_{2n-1})^{T}, ~~{\mathit{\boldsymbol{\delta }}}=(\delta_2, \delta_4, \cdots , \delta_{2n})^{T}, ~~{\mathit{\boldsymbol{\zeta }}}=(t_1, \cdots, t_{2n})^{T}, $

则相应的目标函数变为

(4.24)$\begin{equation}\label{sec3-5} J({\mathit{\boldsymbol{\zeta }}}, {\mathit{\boldsymbol{\mu }}}, {\mathit{\boldsymbol{\delta }}})=S(t_f)+\sum^{n}_{k=1}(P_1\mu_{2k-1}+P_2\delta_{2k}).\end{equation} $

目标函数(4.5)和(4.24)之间的区别是在函数(4.24)中喷洒农药和释放病虫是交替进行的,而在函数(4.5)中两种控制措施被同时实施.

为了简便,令$ {\mathit{\boldsymbol{\tau }}}=(\tau_1, \cdots, \tau_{2n+1})$.经过时间尺度变换和时间平移变换后,模型(4.23)变为

(4.25)$\begin{equation}\label{sec4-26}\left\{ \begin{array}{llll} \left. \begin{array}{ll} \frac{{\rm d}S_i}{{\rm d}s}=f^{i}_{1}(s)=\tau_i\left\{rS_i(s)\left(1-\frac{S_i(s)+\theta I_i(s)}{K}\right)-\frac{\beta S_i(s)I_i(s)}{1+aS_i(s)}\right\}, \\ \frac{{\rm d}I_i}{{\rm d}s}=f^{i}_{2}(s)=\tau_i\left\{\frac{\lambda\beta S_i(s)I_i(s)}{1+aS_i(s)}-wI_i(s)\right\}, \end{array}\right\}s\in(0, 1], \\\left.\begin{array}{ll} S_i(0)=S_{i-1}(1), \\ I_i(0)=I_{i-1}(1)+\delta_{i-1}, \end{array}\right\}i=3, 5, \cdots , 2n+1, \\\left.\begin{array}{llll} S_i(0)=(1-\mu_{i-1})S_{i-1}(1), \\ I_i(0)=(1-\sigma\mu_{i-1})I_{i-1}(1), \end{array}\right\}i=2, 4, \cdots , 2n, \\ ~~\frac{{\rm d}\pi_i}{{\rm d}s}=\tau_i, ~~i=1, \cdots , 2n+1, \\ \end{array}\right.\end{equation}$

具有初始条件(4.14).目标函数最终变为

(4.26)$\begin{equation} J({\mathit{\boldsymbol{\tau }}}, {\mathit{\boldsymbol{\mu }}}, {\mathit{\boldsymbol{\delta }}})=S_{2n+1}(1)+\sum^{n}_{k=1}(P_1\mu_{2k-1}+P_2\delta_{2k}).\end{equation} $

相应的哈密顿函数$H_i, ~i=1, \cdots, 2n+1, $由

(4.27)$\begin{equation}\label{4-28} \left\{ \begin{array}{llll} \left. \begin{array}{llll} \dot{\lambda}^{i}_{1}(s)=-\tau_i\left\{\lambda^{i}_{1}(s)\left(r-\frac{\left(2S_i+\theta I_i\right)r}{K}-\frac{\beta I_i}{\left(1+aS_i\right)^2}\right)+\lambda^{i}_{2}(s)\frac{\lambda\beta I_i}{\left(1+aS_i\right)^2}\right\}, \\ \dot{\lambda}^{i}_{2}(s)=-\tau_i\left\{\lambda^{i}_{1}(s)\left(-\frac{r\theta S_i}{K}-\frac{\beta S_i}{1+aS_i}\right)+\lambda^{i}_{2}(s)\left(\frac{\lambda\beta S_i}{1+aS_i}-w\right)\right\}, \end{array}\right. \\\left.\begin{array}{llll} \lambda^{i}_{1}(1)=\left(1-\mu_ i\right)\lambda^{i+1}_{1}(0), \\ \lambda^{i}_{2}(1)=(1-\sigma\mu_ i)\lambda^{i+1}_{2}(0), \end{array}\right\}i=1, 3, \cdots , 2n-1, \\\left.\begin{array}{llll} \lambda^{i}_{1}(1)=\lambda^{i+1}_{1}(0), \\ \lambda^{i}_{2}(1)=\lambda^{i+1}_{2}(0), \end{array}\right\}i=2, 4, \cdots , 2n \end{array}\right.\end{equation}$

决定,具有横截条件

(4.28)$\begin{equation}\label{4-29}\begin{array}{cc} \lambda^{2n+1}_{1}(1)=1, ~~~~\lambda^{2n+1}_{2}(1)=0.\\ \end{array}\end{equation}$

相应地,目标函数(4.26)关于脉冲时间间隔$\tau_j, ~j=1, \cdots, 2n+1, $的梯度为

(4.29) $ \begin{eqnarray}\label{4-30} \frac{\partial J({\mathit{\boldsymbol{\tau }}}, {\mathit{\boldsymbol{\mu }}}, {\mathit{\boldsymbol{\delta }}})}{\partial\tau_j} &=&\int^{1}_{0}\sum^{2n+1}_{i=1}\frac{\partial H_i(s, S_i(s), I_i(s), {\mathit{\boldsymbol{\lambda }}}^i(s), {\mathit{\boldsymbol{\tau }}}, {\mathit{\boldsymbol{\mu }}}, {\mathit{\boldsymbol{\delta }}})}{\partial \tau_j}{\rm d}s \\ &=&\int^{1}_{0}\left\{\lambda^{j}_{1}(s)\left(rS_j(s)\left(1-\frac{S_j(s)+\theta I_j(s)}{K}\right)-\frac{\beta S_j(s)I_j(s)}{1+aS_j(s)}\right)\right. \\ &&\left.+\lambda^{j}_{2}(s)\left(\frac{\lambda\beta S_j(s)I_j(s)}{1+aS_j(s)}-wI_j(s)\right) \right\}{\rm d}s, \end{eqnarray} $

关于易感害虫的死亡率$\mu_k, ~k=1, 3, \cdots, 2n-1, $和病虫释放量$\delta_l, ~l=2, 4, \cdots, 2n, $的梯度为

(4.30)$\begin{equation}\label{4-31} \frac{\partial J({\mathit{\boldsymbol{\tau }}}, {\mathit{\boldsymbol{\mu }}}, {\mathit{\boldsymbol{\delta }}})}{\partial\mu_{k}} =P_1+\left({\mathit{\boldsymbol{\lambda }}}^{k+1}(0)\right)^{T}\frac{\partial{\mathit{\boldsymbol{\phi }}}_{k}({\mathit{\boldsymbol{\theta }}}_{k}(1), \mu_{k})}{\partial \mu_{k}} =P_1-S_k(1)\lambda^{k+1}_{1}(0)- \sigma I_k(1)\lambda^{k+1}_{2}(0), \end{equation} $

(4.31)$\begin{equation}\label{4-32} \frac{\partial J({\mathit{\boldsymbol{\tau }}}, {\mathit{\boldsymbol{\mu }}}, {\mathit{\boldsymbol{\delta }}})}{\partial\delta_{l}} =P_2+\left({\mathit{\boldsymbol{\lambda }}}^{l+1}(0)\right)^{T}\frac{\partial{\mathit{\boldsymbol{\phi }}}_{l}({\mathit{\boldsymbol{\theta }}}_{l}(1), \delta_{l})}{\partial \delta_{l}} =P_2+\lambda^{l+1}_{2}(0). \end{equation}$

本小节提出了一个喷洒农药和释放病虫交替进行的最优害虫控制问题.接下来,我们将研究害虫治理问题中最简单的控制准则.

假设在固定时刻$t=i\tau, ~i=1, \cdots, N-1, $杀虫剂喷洒量和病虫释放量是不变的,我们建立并研究如下模型

(4.32)$\begin{equation}\label{sec3-23}\left\{ \begin{array}{ll} \left.\begin{array}{ll} \frac{{\rm d}S}{{\rm d}t}=rS(t)\left(1-\frac{S(t)+\theta I(t)}{K}\right)-\frac{\beta S(t)I(t)}{1+aS(t)}, \\ \frac{{\rm d}I}{{\rm d}t}=\frac{\lambda\beta S(t)I(t)}{1+aS(t)}-wI(t), \end{array}\right\}t\neq i\tau, \\ \left.\begin{array}{ll} S(t^{+})=(1-\mu)S(t), \\ I(t^{+})=(1-\sigma\mu)I(t)+\delta, \end{array}\right\}t=i\tau, ~i=1, \cdots , N-1, \\ \end{array}\right.\end{equation} $

具有初始条件(4.2),定义相应的目标函数为

(4.33)$\begin{equation}\label{sec3-24}J({\mathit{\boldsymbol{\mu }}}, {\mathit{\boldsymbol{\delta }}})=S(t_f)+(N-1)(P_1\mu+P_2\delta).\end{equation} $

目标函数(4.24)和(4.33)之间的主要区别为在$J({\mathit{\boldsymbol{\zeta }}}, {\mathit{\boldsymbol{\mu }}}, {\mathit{\boldsymbol{\delta }}})$中需要优化人为干预的时刻,而且喷洒农药和释放病虫是交替进行的,但在$J({\mathit{\boldsymbol{\mu }}}, {\mathit{\boldsymbol{\delta }}})$中人为干预的时刻是确定的,而且两种控制措施在同一时刻被实施.经过时间缩放和时间平移变换,系统(4.32)变为

(4.34)$\begin{equation}\label{sec3-25}\left\{ \begin{array}{llll} \left. \begin{array}{ll} \frac{{\rm d}S_i}{{\rm d}s}=f^{i}_{1}(s)=\tau\left\{rS_i(s)\left(1-\frac{S_i(s)+\theta I_i(s)}{K}\right)-\frac{\beta S_i(s)I_i(s)}{1+aS_i(s)}\right\}, \\ \frac{{\rm d}I_i}{{\rm d}s}=f^{i}_{2}(s)=\tau\left\{\frac{\lambda\beta S_i(s)I_i(s)}{1+aS_i(s)}-wI_i(s)\right\}, \end{array}\right\}s\in(0, 1], \\\left. \begin{array}{ll} S_i(0)=(1-\mu)S_{i-1}(1), \\ I_i(0)=(1-\sigma\mu)I_{i-1}(1)+\delta, \end{array}\right\}i=2, \cdots , N, \\ ~~ \frac{{\rm d}\pi_i}{{\rm d}s}=\tau, ~i=1, \cdots , N, \\ \end{array}\right.\end{equation} $

具有初始条件(4.14),相应的目标函数(4.33)变为

(4.35)$\begin{equation}\label{sec3-26}J({\mathit{\boldsymbol{\mu }}}, {\mathit{\boldsymbol{\delta }}})=S_{N}(1)+(N-1)(P_1\mu+P_2\delta), \end{equation} $

并且哈密顿函数由

(4.36)$\begin{equation}\label{sec3-27}\left\{ \begin{array}{llll} \left. \begin{array}{llll} \dot{\lambda}^{i}_{1}(s) =-\frac{\partial H_i}{\partial S_i}=-\tau\left\{\lambda^{i}_{1}(s)\left(r-\frac{\left(2S_i+\theta I_i\right)r}{K}-\frac{\beta I_i}{\left(1+aS_i\right)^2}\right)+\lambda^{i}_{2}(s)\frac{\lambda\beta I_i}{\left(1+aS_i\right)^2}\right\}, \\ \dot{\lambda}^{i}_{2}(s) =-\frac{\partial H_i}{\partial I_i}=-\tau\left\{\lambda^{i}_{1}(s)\left(-\frac{r\theta S_i}{K}-\frac{\beta S_i}{1+aS_i}\right)+\lambda^{i}_{2}(s)\left(\frac{\lambda\beta S_i}{1+aS_i}-w\right)\right\}, \end{array}\right. \\\left.\begin{array}{llll} \lambda^{i}_{1}(1)=\left(1-\mu\right)\lambda^{i+1}_{1}(0), \\ \lambda^{i}_{2}(1)=(1-\sigma\mu)\lambda^{i+1}_{2}(0), \end{array}\right\}i=1\cdots , N-1 \end{array}\right.\end{equation}$

决定,具有横截条件(4.18).

经过计算得到目标函数(4.35)关于易感害虫的死亡率$\mu$和病虫释放量$\delta$的梯度分别为

(4.37)$\begin{eqnarray}\label{sec3-28} \frac{\partial J(\mu, \delta)}{\partial \mu} &=&P_1(N-1)+\sum\limits_{i=1}^{N-1}\left({\mathit{\boldsymbol{\lambda }}}^{i+1}(0)\right)^{T} \frac{\partial{\mathit{\boldsymbol{\phi }}}_{i}({\mathit{\boldsymbol{\theta }}}_{i}(1), \mu, \delta)}{\partial \mu} \\ &=&P_1(N-1)-\sum\limits_{i=1}^{N-1}\left\{S_i(1)\lambda^{i+1}_{1}(0)+\sigma I_i(1)\lambda^{i+1}_{2}(0)\right\}, \end{eqnarray}$

(4.38)$\begin{eqnarray} \label{sec3-29} \frac{\partial J(\mu, \delta)}{\partial \delta} &=&P_2(N-1)+\sum\limits_{i=1}^{N-1}\left({\mathit{\boldsymbol{\lambda }}}^{i+1}(0)\right)^{T}\frac{\partial{\mathit{\boldsymbol{\phi }}}_{i}({\mathit{\boldsymbol{\theta }}}_{i}(1), \mu, \delta)}{\partial \delta} \\ &=&P_2(N-1)+\sum\limits_{i=1}^{N-1}\lambda^{i+1}_{2}(0).\end{eqnarray}$

对于上述最简单的最优害虫控制问题,在每次确定的脉冲时刻目标函数关于由于喷洒农药导致的易感害虫的死亡率以及有病害虫释放量的梯度被计算出来,这对寻找最优害虫控制策略是至关重要的.目前为止,基于不同脉冲释放频率和数量的三种最优害虫控制问题被描述出来.接下来,我们将模拟这三种情况从而找到最有效的策略.

我们所感兴趣的是确定合适的控制参数,即脉冲时间间隔$\tau_i, $由于喷洒杀虫剂导致的易感害虫的减少比例$\mu_i$,以及病虫的释放量$\delta_i$,从而获得最优的目标函数.因此,在这一节中我们将研究第四节所描述的三种控制策略是如何成功地影响害虫控制,故将对系统(4.32), (4.23)和(4.1)分别进行数值模拟实验,进而建议一种最有效的策略用于未来的害虫控制.

取定参数

(5.1)$ \begin{equation}\label{parameter} \begin{array}{ll} &r =10, ~ \theta=0.2, ~ K=1000, ~ \beta =0.8, ~ a=0.001, \\ &w=0.2, ~ \lambda=0.02, ~ \sigma=0.001, ~P_1=1.8, ~P_2=2, ~ t_f=50, \end{array} \hspace{40pt} \end{equation}$

种群初始密度$~S(0)=20, ~I(0)=12, $且天作为时间单位.

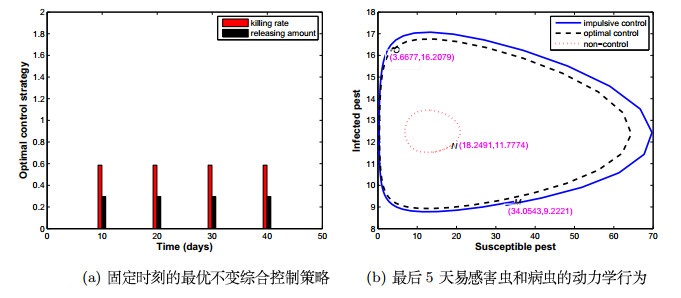
模拟1  固定时刻的不变综合控制的优化策略

假设脉冲周期$\tau=10, $即在脉冲时间点$~t_1=10, ~t_2=20, ~t_3=30, ~t_4=40$对易感害虫和染病害虫种群进行人为干预.我们将最优选择由于喷洒农药导致的易感害虫的死亡率$\mu$和染病害虫的释放量$\delta$使目标函数即终端观测时刻易感害虫的数量以及控制措施的花费成本实现最小.

假设由于喷洒杀虫剂导致的易感害虫的死亡率$\mu$和病虫释放量$\delta$的约束如下

(5.2)$\begin{equation}\label{re} 0.1\leqslant\mu\leqslant0.6, ~~~~0.2\leqslant\delta\leqslant3.\end{equation} $

通过利用matlab软件从初始值$\mu_0=0.2$, $\delta_0=1$进行数值模拟获得最优控制策略$\mu^*=0.5866$, $\delta^*=0.2969$,同时目标函数达到最优值$J^*=10.2645, $终端观测时刻易感害虫的数量$S^*(t_f)=3.6677.$图 1(a)表明,在当前情况下释放较少的病虫有利于实现最优控制的目标. 图 1(b)分别描绘了在最优脉冲控制,初始脉冲控制和无脉冲控制准则下易感害虫和有病害虫在最后5天内的数量演变规律.其中黑色虚线表示在最优脉冲控制$~\delta^*=0.2969$和$\mu^*=0.5866$下种群的轨迹,蓝色实线表示在初始脉冲控制$\delta_0=1$和$\mu_0=0.2$下种群的轨迹.$ O (3.6677, 16.2079), M (34.0543, 9.2221)$和$N (18.2491, 11.7774) $则分别表示在最优脉冲控制,初始脉冲控制,以及无脉冲控制准则下易感害虫和有病害虫在终端观测时刻的数量坐标.

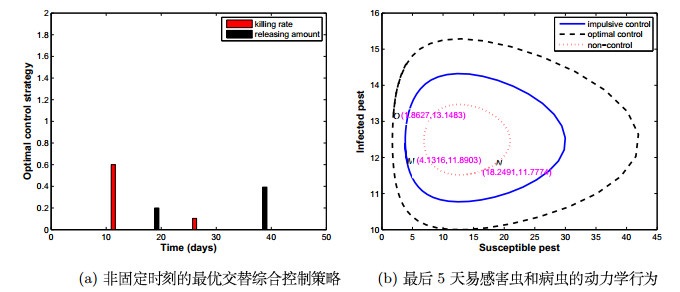
模拟2  非固定时刻的交替综合控制的优化策略

假设脉冲时间间隔,由于喷洒杀虫剂导致的易感害虫的死亡率及染病害虫释放量的初始值为

(5.3)$\begin{equation}\label{alter tau para} \tau_{10}=\tau_{20}=\tau_{30}=\tau_{40}=\tau_{50}=10, \end{equation} $

(5.4)$\begin{equation}\label{alter mu para} \mu_{10}=\mu_{30}=0.2, ~~\delta_{20}=\delta_{40}=1, \end{equation} $

并且时间间隔满足约束$1\leqslant\tau_i\leqslant 20, ~i=1, 2, \cdots, 5.$通过数值模拟,我们得到了最优的脉冲时间间隔,易感害虫的死亡率以及病虫释放量

(5.5)$\begin{equation}\label{opt tau para} \tau^{*}_1=11.2839, ~\tau^{*}_2=7.9073, ~\tau^{*}_3=6.8790, ~\tau^{*}_4=12.7458, ~\tau^{*}_5=11.1840, \end{equation} $

(5.6)$\begin{equation}\label{opt amou para} \mu^{*}_1=0.6, ~\mu^{*}_3=0.1039, ~\delta^{*}_2=0.2, ~\delta^{*}_4=0.3932. \end{equation} $

以及终端观测时刻易感害虫的数量$S^*(t_f)=1.8627$,且目标函数的最优值$~J^*=4.3162.$由(5.5)式可得

(5.7)$\begin{equation}\label{opt time} t^{*}_1=11.2839, ~t^{*}_2=19.1912, ~t^{*}_3=26.0702, ~t^{*}_4=38.816. \end{equation}$

图 2(a)描述了由(5.6)和(5.7)式决定的最优脉冲控制策略,该图说明在脉冲时间点$t^{*}_1=11.2839, ~t^{*}_3=26.0702$喷洒农药杀虫剂,在$t^{*}_2=19.1912, ~t^{*}_4=38.816$释放病虫的控制效果更好.在最优脉冲控制,初始脉冲控制和无脉冲控制准则下易感害虫和病虫在最后5天内的数量演变情况见图 2(b).其中点$ O (1.8627, 13.1483), M (4.1316, 11.8903) $和$N (18.2491, 11.7774)$分别表示在最优脉冲控制,初始脉冲控制,以及无脉冲控制准则下易感害虫和染病害虫在终端观测时刻的数量坐标,显然最优脉冲控制的效果更好.进一步研究

(5.8)$ \begin{equation}\label{alter} \delta_{10}=\delta_{30}=1, ~~\mu_{20}=\mu_{40}=0.2, \end{equation}$

情况下的脉冲控制策略,即只在第一个和第三个脉冲时间点释放病虫,只在第二个和第四个脉冲时间点喷洒农药,通过数值模拟获得最优值

(5.9)$\begin{equation}\label{jijun tau} \tau^{*}_1=15.1979, ~\tau^{*}_2=15.2035, ~\tau^{*}_3=7.6550, ~\tau^{*}_4=7.1583, ~\tau^{*}_5=4.7853, \end{equation}$

(5.10) $ \begin{equation}\label{jijun amou}\delta^*_{1}=0.2, ~\delta^*_{3}=1.2905, ~\mu^*_{2}=0.5463, ~\mu^*_{4}=0.1, ~S^*(t_f)=0.9569, ~J^*=5.1012. \end{equation} $

该结果表明喷洒农药和释放病虫的顺序也会影响目标函数的取值.显然,只在第一个和第三个脉冲时间点释放病虫,第二个和第四个脉冲时间点喷洒农药的策略不太令人满意,因为它对目标函数的影响较小.

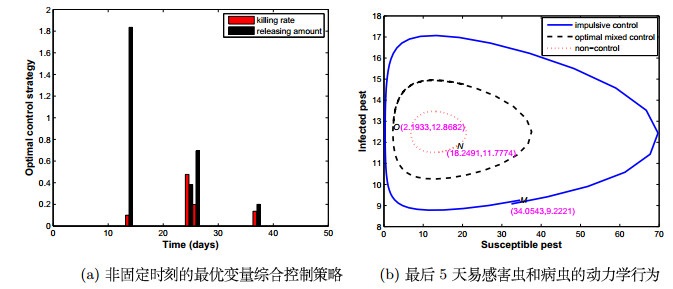
模拟3  非固定时刻的变量综合控制的优化策略

假设脉冲时间间隔的初始值由(5.3)式给定,由于喷洒农药使易感害虫减少的比例和病虫释放量的初始值为

(5.11)$\begin{equation}\label{varia mu para} \mu_{i0}=0.2, ~~~~\delta_{i0}=1, ~~i=1, \cdots , 4. \end{equation}$

同样地利用Matlab软件进行数值模拟获得脉冲间隔,农药致死率和病虫释放量的最优值

(5.12)$ \begin{equation}\label{vari opt tau}\tau^{*}_1=13.9982, ~\tau^{*}_2=10.9573, ~\tau^{*}_3=1, ~\tau^{*}_4=11.1756, ~\tau^{*}_5=12.8688, \end{equation} $

(5.13)$\begin{equation}\label{vari opt amou mu} \mu_1^*=0.1, ~\mu_2^*=0.4771, ~\mu_3^*=0.1990, ~\mu_4^*=0.1365, \end{equation}$

(5.14)$ \begin{equation}\label{vari opt amou del} \delta_1^*=1.8346, ~\delta_2^*=0.3812, ~\delta_3^*=0.6944, ~\delta_4^*=0.2, \end{equation} $

以及相应的目标函数$J^*=9.3975$,易感害虫的数量$S^*(t_f)=2.1933.$图 3(a)所示的最优脉冲控制策略表明从优化的角度来说,我们在脉冲时间点$t^{*}_1=13.9982, ~t^{*}_2=24.9555, ~t^{*}_3=25.9555, ~t^{*}_4=37.1311$喷洒农药和释放病虫进行害虫治理的效果会更好. 图 3(b)描绘了最后5天内易感害虫和染病害虫的时间序列图,其中$O (2.1933, 12.8682), M (34.0543, 9.2221) $和$N (18.2491, 11.7774)$分别表示最优脉冲控制,初始脉冲控制和无脉冲控制准则下终端观测时刻的种群水平.

为了对不同害虫控制策略的效果进行对比,现将三种控制策略的最优结果如表 1.

表 1说明非固定时刻的变量综合控制的优化效果优于固定时刻的不变综合控制,并且非固定时刻的交替综合控制优于非固定时刻的变量综合控制.显然,模拟2和模拟3相比,目标函数值和易感害虫的数量减少很多.事实上,喷洒农药不仅会杀死易感害虫还会大量捕杀非目标昆虫,因此非固定时刻的交替综合控制会带来更少的伤害.该结果表明,非固定时刻的交替综合控制策略在害虫治理工作中扮演着重要的角色,这为未来的害虫监管提供了理论指导.

根据粮食及农业组织(粮农组织)的报道,害虫与人类之间的"战争"已持续上千年,因此如何有效地控制害虫成为日益重要的问题.为了减少对非目标生物的伤害,提高环境质量,以及降低害虫的抗药性,过多的利用单一的控制策略是不可取的,应用尽可能互相配合的方式来控制害虫种群数量,防止农作物受其侵害.

考虑到农药的副作用,释放有病害虫作为一种有价值的非化学工具在害虫治理的过程中变得越来越重要.受到文献[11]和[35]的研究工作的启发,本文研究了一类害虫管理$SI$传染病模型.虽然该模型具有多种动力学行为但易感害虫不能灭绝.为此,在该模型中引入多次脉冲干预措施,得到了易感害虫灭绝周期解全局渐近稳定的充分条件.然而,从生态和经济方面来说,让易感害虫灭绝的策略是不可取的,这是因为田间适当数量的害虫对于保护天敌,以及维持农作物的经济补偿是有益的.因此,用最小的成本最小化害虫在终端时刻的数量,基于不同的控制策略,三种最优害虫控制问题被详细研究.通过时间缩放和时间平移变换的方法,计算了目标函数关于脉冲时间间隔,农药致死率和病虫释放量的梯度,这对获得最优害虫控制策略是至关重要的.最后,数值模拟的结果显示,与其他两种策略相比,非固定时刻的交替综合控制策略是最有效的.

现在将这些优化结果与易感害虫灭绝周期解全局渐近稳定的充分条件进行比较.把(5.1)式的参数和模拟1的最优参数带入不等式(3.3)中, (3.3)式不成立,该结果说明了这些参数不能保证易感害虫灭绝周期解的吸引性.为此,选取$\mu=0.9, ~\delta=25, $带入(3.3)式,得到$-0.2359<2.3026.$然后再利用(5.1)式的参数,得到目标函数206.48.该结果说明尽管易感害虫灭绝,但是由于控制措施成本较高,所以这并不是一个最佳的解决方案.

尽管本文中我们在害虫治理工作的研究方面做了一些努力,但在未来应该去探讨更广泛的课题: (1)在害虫治理中把终端时刻作为控制变量是有意义的; (2)优化脉冲干预的次数值得探索; (3)有关农作物和害虫生长规律的实际数据对于实现有效的害虫管理是必要的.