1 引言
迭代是自然科学和人类生活中的常见现象,在函数方程和动力系统中广泛存在[6, 8, 9]. 对映射迭代的研究通常为迭代根问题和迭代函数方程提供新思路和新方法. 然而映射迭代的计算是异常困难的,即使对于一些特殊函数,比如多项式和幂级数[14]、折线函数[7, 19] 和逐段单调函数[17, 18].以上这些特殊函数都是单值函数. 另一方面,集值函数作为一类重要映射,在控制理论[5]、人工智能[10]、统计学[2]及经济学[15]等学科中广泛应用.关于集值函数理论,参见文献[1, 3].
目前,在单个集值点的集值函数迭代方面已有结果. 这类函数的迭代根问题最早出现在文献[4]中,该文献给出了迭代根不存在的充分条件. 后来,文献[11]进一步获得新的迭代根不存在条件,并给出严格单调且上半连续(记为USC)集值函数的二次迭代根存在条件.最近,针对一类高阶集值迭代方程,文献[12]给出无穷多单增的USC集值解的一般构造方法.除了构造法,文献[13, 16] 还利用不动点定理获得集值解的存在性.
本文研究USC集值函数的迭代规律,首先引入如下基本定义.设$I:=[a,b]\subset {\Bbb R},$ 集值函数$f:I\rightarrow 2^I$,定义$f(A):=\bigcup\limits_{x\in A} f(x)$,其中$A\subset I$为一个子区间.对任意给定的正整数$n$,集值函数$f:I\to 2^I$的$n$次迭代是$f$的$n$次复合
$$f^n(x):=\bigcup_{y\in f^{n-1}(x)} G(y),
$$其中$f^0(x):=\{x\},x\in I$. 若$\#f(t_0)\geq 2,$ 则称$t_0\in (a,b)$是$f$的集值点.记${\cal S}(I,I)$为所有除了集值点外都连续的集值函数$f: I\to 2^I$的集合. 记$N(f)$为$f$的集值点个数.本文研究一类单集值点的USC集值函数$f\in{\cal S}(I,I)$的迭代,具体形式如下\begin{equation}f(t)=\left\{\begin{array}{ll}f_1 (t),& a\leq t < t_0,\\{[c,d],}& t=t_0,\\f_2 (t),~~& t_0 < t \leq b,\end{array}\right.\label{f(t)}\end{equation}其中$[c,d]\subset I$,函数$f_1$,$f_2$ 在定义区间上连续、严格单调且满足
$$\lim\limits_{t\rightarrow {t_0}^{-}}f(t) =c,\ \lim\limits_{t\rightarrow {t_0}^{+}}f(t) =d.
$$我们证明$f$在$n$次迭代后的集值点个数$N(f^n)$由$f(a),\ f(b),\ f(c),\ f(d)$及$f$的不动点唯一确定,并分别给出$N(f^n)(n\rightarrow\infty)$恒定、有界及无穷的充分条件. 这种方法不仅适用于有限个集值点的USC函数,也适用于定义在实数域上的USC集值函数,我们将在第三部分举例说明.
2 主要结果
该部分具体讨论USC集值函数(1.1)的迭代. 我们依据集值函数在子区间上的严格单调性,将该类函数分成四种情况并分别给出$N(f^n)(n\rightarrow\infty)$恒定、有界及无穷的充分条件. 详细结论在表格1-4中列出.
2.1 $f_1,\ f_2$ 严格递增
表1
Table 1
表1(Table 1)
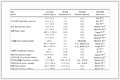
表1 $f_1,\ f_2$ 严格递增, 其中$A$, $B$ 为正整数
|
表1 $f_1,\ f_2$ 严格递增, 其中$A$, $B$ 为正整数
|
定理2.1 令$f\in{\cal S}(I,I)$具有形式(1.1),其中$f_1,f_2$严格递增.
(i) 若$d\geq t_0 \geq c,$ 则对任意的整数$n\geq 1$,
$N(f^n)=1$;
(ii) 若$t_0 >f(b)$ (或$ f(a)>t_0),$则对任意的整数$n\geq 1,
$$N(f^n)=1$;
(iii) 若$f(a)=t_0$ (或 $f(b)=t_0 ),$则对任意的整数$n\geq 2,
$$N(f^n)=2.$
证 情况(i),由假设$d\geq t_0 \geq c$和$f_1$,$f_2$严格递增,我们知$f(a) < c < t_0 < d < f(b).$于是$f([a,t_0))\subset[a,t_0),f((t_0,b])\subset(t_0,b].$因此,对任意的正整数$n\geq1,$
|
$\begin{eqnarray}f^n (t)=\left\{\begin{array}{ll}{f_1}^n (t),& a\leq t < t_0,\\{[{f}^{n-1}(c),{f}^{n-1}(d)],}~~& t=t_0,\\{f_2}^n (t),& t_0 < t \leq b\end{array}\right.\label{thm1i1}\end{eqnarray}$
|
(2.1)
|
成立,即$N(f^n)=1,n=1,2,\cdots $.
情况(ii),由条件$t_0 >f(b)$ (或$f(a)>t_0)$及$f_1,f_2$的严格单调性,我们得到$f(I)\subset [a,t_0)$ (或 $f(I)\subset (t_0 ,b]).$于是,对任意的整数$n\geq 1,$ 有
|
$\begin{eqnarray}f^n (t)=\left\{\begin{array}{ll}{f_1}^n (t),& a\leq t < t_0,\\{[{f}^{n-1}(c),{f}^{n-1} (d)],}~~& t=t_0,\\{f_1}^{n-1}\circ f_2 (t),& t_0 < t \leq b\end{array}\right.\label{thm1ii1}\end{eqnarray}$
|
(2.2)
|
(或
|
$\begin{eqnarray}f^n (t)=\left\{\begin{array}{ll} {f_2}^{n-1}\circ f_1 (t),& a\leq t < t_0,\\ {[{f}^{n-1} (c),{f}^{n-1}(d)],}~~& t=t_0,\\ {f_2}^n (t),& t_0 < t \leq b\end{array}\right.~)\label{thm1ii2}\end{eqnarray}$
|
(2.3)
|
成立,即$N(f^n)=1,n=1,2,\cdots $.
情况(iii),条件$f(a)=t_0$ (或$f(b)=t_0 )$说明端点$a$ (或 $b)$ 是$f^2$的集值点. 于是$f^2 (I)\subset (t_0 ,b]$ (或$f^2 (I)\subset [a,t_0)).$对任意的整数$n\geq 2,$ 有
|
$\begin{eqnarray}f^n (t)=\left\{\begin{array}{ll}{ [f^{n-2}(c),f^{n-2}(d)],}~~& t=a,\\ {f_2}^{n-1} \circ f_1 (t),&a< t < t_0,\\{ [f^{n-1}(c),f^{n-1}(d)],}& t=t_0,\\ {f_2}^n (t),& t_0 < t \leq b\end{array}\right.\label{thm1iii1}\end{eqnarray}$
|
(2.4)
|
(或
|
$\begin{eqnarray}f^n (t)=\left\{\begin{array}{ll}{f_1}^n (t),& a\leq t < t_0,\\{[f^{n-1}(c),f^{n-1}(d)],}~~& t=t_0,\\{f_1}^{n-1} \circ f_2 (t),& t_0 < t < b,\\{[f^{n-2}(c),f^{n-2}(d)],}& t=b\end{array}\right.~),\label{thm1iii2}\end{eqnarray}$
|
(2.5)
|
即$N(f^n)=2,n=2,3,\cdots $.
定理2.2 令$f\in{\cal S}(I,I)$具有形式(1.1),其中$f_1,f_2$严格递增.
(i) 若$f$在区间$(t_0,b]$上无不动点且$f(b)>t_0 >d,$则$N(f^n)(n\rightarrow\infty)$有界;
(ii) 若$f$在区间$[a,t_0)$上无不动点且$c>t_0 >f(a),$则$N(f^n)(n\rightarrow\infty)$有界.
证 情况(i),鉴于$f$在$(t_0,b]$上无不动点且$f(b)>t_0 >d$,我们得到$f(t)<t,\ t\in(t_0 ,b].$ 因为$f$在$(t_0 ,b]$上的严格单调性,必存在正整数$m$使得$$\begin{eqnarray*}f^m (b)< t_0 \leq f^{m-1} (b)<\cdots <f(b).\end{eqnarray*}$$所以$f^m (t)\subseteq[a,t_0),t\in [a,b]$ 且迭代$f^n\ (n\geq m+1)$一直保持在严格单调子区间$[a,t_0)$上进行.从而,$f^n (n\geq m+1)$的集值点个数保持不变,即$N(f^n)=N(f^m),$ 有界性得到证明.
类似地,可以证明情况(ii).
定理2.3 令$f\in{\cal S}(I,I)$具有形式(1.1),其中$f_1,f_2$ 严格递增.
(i) 若$f$在$(t_0,b]$存在不动点且$t_0 >d,$则$\lim\limits_{n\rightarrow\infty}N(f^n)=\infty$;
(ii) 若$f$在$[a,t_0)$存在不动点且$c>t_0,$则$\lim\limits_{n\rightarrow\infty}N(f^n)=\infty.$
证 情况(i),不失一般性,假设$t_1$是$f$在$(t_0,b]$上的最小不动点. 注意到${\rm max}f(t_0)=d<t_0,f(t_1)=t_1>t_0$,必存在点$\tilde{t}_1 \in(t_0,t_1)$使得$f(\tilde{t}_1)=t_0.$由此我们能归纳地找到$n-1$个点$t_0 <\tilde{t}_1 <\tilde{t}_2 <\cdots <\tilde{t}_{n-1}<t_1$满足$f(\tilde{t}_i)=\tilde{t}_{i-1},i=2,3,\cdots ,n-1,$ 即
|
$\begin{equation}t_0 =f(\tilde{t}_1)=f^2 (\tilde{t}_2)=\cdots =f^{n-1} (\tilde{t}_{n-1}).\label{thm3i}\end{equation}$
|
(2.6)
|
这说明$t_0 ,\tilde{t}_1 ,\ \tilde{t}_2 ,\ \cdots ,\ \tilde{t}_{n-1}$都是$f^n$的集值点,从而$\lim\limits_{n\rightarrow\infty}N(f^n)=\infty$.
情况(ii)的证明类似于(i).
2.2 $f_1,\ f_2$ 严格递减
定理2.4 令$f\in{\cal S}(I,I)$具有形式(1.1),其中$f_1,f_2$严格递减.
(i) 若$f(a)<t_0,\ d\leq t_0$ (或$t_0<f(b),\ t_0 \leq c),$则对任意的整数$n\geq1,$ $N(f^n)=1$;
(ii) 若 $f(a)<t_0 <\min\{f(b),d\},$则对任意的整数$n\geq1,$ $N(f^n)=1$;
(iii) 若$d\leq t_0 =f(a),a<f(b)$ (或$f(b)=t_0 \leq c),$则对任意的整数$n\geq2,$ $N(f^n)=2$;
(iv) 若$f(a)=t_0 <f(b)$ (或$f(a)<t_0=f(b)),$则对任意的整数$n\geq2,$ $N(f^n)=2$;
(v) 若$\max\{f(a),f(b)\}<t_0 \leq f(d)$ (或$f(c)\leq t_0<\min\{f(a),f(b)\}),$则对任意的整数$n\geq2,$ $N(f^n)=2$;
(vi) 若$f(a)=f(b)=t_0$ (或$f(a)=t_0 \leq f(d),\ a<f(b)<t_0$ 或$f(c)\leq t_0 =f(b),\ t_0<f(a)),$则对任意的整数$n\geq2,$ $N(f^n)=3$;
(vii) 若$d\leq t_0=f(a),\ f(b)=a$,则对任意的整数$n\geq3,$ $N(f^n)=3$;
(viii) 若$f(a)=t_0 \leq f(d),\ f(b)=a,$则对任意的整数$n\geq3,$ $N(f^n)=4.$
证 情况(i),条件$f(a)<t_0,\ d\leq t_0$ (或 $t_0<f(b),\ t_0 \leq c)$表明$f(I)\subset [a,t_0]$ (或 $f(I)\subset [t_0,b]),$从而迭代公式(2.2) (或 (2.3)) 成立.于是,对任意的整数$n\geq 1,$ 有$N(f^n)=1.$情况(ii),由$f_1 ,f_2$的假设条件和严格单调性,我们容易得到$c<f(a)<t_0 <f(b)<d.$仿照定理2.1情况(i)的讨论,利用公式(2.1)证明情况(ii).
情况(iii),由假设$d\leq t_0 =f(a),a < f(b)$ (或 $f(b)=t_0 \leq c)$ 我们知道$a$ (或 $b)$是$f^2$的集值点且$f^2 (I)\subset [a,t_0]$ (或 $f^2 (I)\subset [t_0,b])$. 因此,对任意的整数$n\geq 2,$ 有
|
$\begin{eqnarray}f^n (t)=\left\{\begin{array}{ll} {f}^{n-2}([c,d]),&t=a,\\ {f_1}^n (t),&a < t < t_0,\\{f}^{n-1}([c,d]),& t=t_0,\\{f_1}^{n-1}\circ f_2 (t),~~& t_0 < t \leq b\end{array}\right.\label{thm4iii1}\end{eqnarray}$
|
(2.7)
|
(或
|
$\begin{eqnarray}f^n (t)=\left\{\begin{array}{ll}{f_2}^{n-1}\circ f_1 (t),~~& a\leq t < t_0,\\{f}^{n-1} ([c,d]),& t=t_0,\\{f_2}^n (t),& t_0 < t < b,\\f^{n-2}([c,d]),&t= b\end{array}\right.~).\label{thm4iii2}\end{eqnarray}$
|
(2.8)
|
从而$N(f^n)=2,n=2,3,\cdots $.
表2
Table 2
表2(Table 2)

表2 $f_1,\ f_2$ 严格递减, 其中 $C$, $D$, $E$ 是正整数
|
表2 $f_1,\ f_2$ 严格递减, 其中 $C$, $D$, $E$ 是正整数
|
(iv)的证明类似于(iii).
情况(v),注意到$f(b)<t_0<d$ (或 $c<t_0<f(a)$),必存在$\tilde{t}_0 \in(t_0 ,b)$ (或 $\bar{t}_0 \in(a,t_0))$使得$f(\tilde{t}_0)=t_0$ (或 $f(\bar{t}_0)=t_0)$成立.因此$\tilde{t}_0 $ (或 $\bar{t}_0 )$ 是 $f^2$ 的一个集值点且满足包含关系
$$f([a,t_0))\subset[a,t_0),\ f((t_0,\tilde{t}_0))\subset(t_0,d),\ f((\tilde{t}_0,b])\subset[a,t_0)
$$(或
$$f([a,\bar{t}_0))\subset(t_0,b],\ f((\bar{t}_0,t_0))\subset(c,t_0),\ f((t_0,b])\subset(t_0,b]).
$$另外,条件$f(d)\geq t_0$ 导出 $t_0<d\leq \tilde{t}_0$. 于是$f((t_0,\tilde{t}_0))\subset(t_0,d)\subset (t_0,\tilde{t}_0)$,这说明 $f$ 是 $(t_0,\tilde{t}_0)$上的自映射. 从而,对任意的整数$n\geq 2$
|
$\begin{eqnarray}f^n (t)=\left\{\begin{array}{ll}{f_1}^n (t),& a\leq t < t_0,\\{f}^{n-1}([c,d]),& t=t_0,\\{f_2}^n (t),& t_0 < t <\tilde{t}_0 ,\\{f}^{n-2}([c,d]),& t=\tilde{t}_0 ,\\{f_1}^{n-1} \circ f_2 (t),~~& \tilde{t}_0 <t\leq b\end{array}\right.\label{thm4v1}\end{eqnarray}$
|
(2.9)
|
(或
|
$\begin{eqnarray}f^n (t)=\left\{\begin{array}{ll}{f_2}^{n-1} \circ f_1 (t),~~ & a\leq t < \bar{t}_0,\\{f}^{n-2}([c,d]),& t=\bar{t}_0,\\{f_1}^{n} (t),& \bar{t}_0 <t<t_0,\\{f}^{n-1}([c,d]),& t=t_0,\\{f_2}^n (t),& t_0 < t \leq b\end{array}\right.~).\label{thm4v212}\end{eqnarray}$
|
(2.10)
|
即 $N(f^n)=2,n=2,3,\cdots $.
情况(vi),因$f(a)=f(b)=t_0,$ 所以$a$与 $b$都是$f^2$的集值点且$f((a,t_0))\subset(a,t_0),$ $ f((t_0,b))\subset(t_0,b).$于是,对任意的整数$n\geq2,
$$$f^n (t)=\left\{\begin{array}{ll}{f}^{n-2}([c,d]),~~ & t=a,\\ {f_1}^n (t),& a < t < t_0,\\ {f}^{n-1}([c,d]),& t=t_0,\\ {f_2}^n (t),& t_0 < t < b ,\\ {f}^{n-2}([c,d]),& t=b ,\end{array}\right.
$$即$N(f^n)=3,n=2,3,\cdots $.
现在考虑(vi)中的另外两个条件. 首先由条件$a<f(b)<t_0 <d$ (或 $c<t_0 <f(a)$)可知存在点$\hat{t}_0$ (或 $\check{t}_0)$满足$f(\hat{t}_0)=t_0$ (或 $f(\check{t}_0)=t_0).$又因为$f(a)=t_0$ (或 $f(b)=t_0),$ 我们知道 $a$ (或 $b)$ 也是$f^2$的一个集值点. 从而,$f^2$ 有三个集值点$a,\ t_0,\ \hat{t}_0$ (或 $\check{t}_0,\ t_0,\ b).$ 我们注意到,条件$f(d)\geq t_0$说明下面的包含关系成立
$$f((a,t_0))\subset(a,t_0),\ f((t_0,\hat{t}_0))\subset(t_0,\hat{t}_0),\ f((\hat{t}_0,b))\subset(a,t_0),
$$(或者由 $f(c)\leq t_0$得到
$$f((a,\check{t}_0))\subset(t_0,b),\ f((\check{t}_0,t_0))\subset(\check{t}_0,t_0),\ f((t_0,b))\subset(t_0,b)).
$$从而,对任意的整数$n\geq2,
$$$f^n (t)=\left\{\begin{array}{ll} {f}^{n-2}([c,d]),& t=a,\\ {f_1}^n (t),&a< t < t_0,\\ {f}^{n-1}([c,d]),& t=t_0,\\ {f_2}^n (t),& t_0 < t <\hat{t}_0 ,\\ {f}^{n-2}([c,d]),& t=\hat{t}_0 ,\\ {f_1}^{n-1}\circ f_2 (t),~~ &\hat{t}_0 <t\leq b \end{array}\right.
$$(或
$$f^n (t)=\left\{\begin{array}{ll}{f_2}^{n-1}\circ f_1 (t),~~ & a\leq t<\check{t}_0,\\{f}^{n-2}([c,d]),& t=\check{t}_0 ,\\ {f_1}^n (t),& \check{t}_0 <t<t_0 ,\\ {f}^{n-1}([c,d]),& t=t_0,\\ {f_2}^n (t),&t_0 <t<b,\\ {f}^{n-2}([c,d]),& t=b \end{array}\right.~),
$$即$N(f^n)=3,n=2,3,\cdots $.
情况(vii),条件$f(a)=t_0\geq d,f(b)=a$ 表明$a$ 及 $b$都是 $f^3$的集值点且成立包含关系$f((a,t_0))\subset[a,t_0),f((t_0,b))\subset[a,t_0)$. 因此,对任意的整数$n\geq3$有
$$f^n (t)=\left\{\begin{array}{ll} {f}^{n-2}([c,d]),~~ &t=a,\\ {f_1}^n (t),& a< t < t_0,\\ {f}^{n-1}([c,d]),& t=t_0,\\ {f_1}^n (t),& t_0 < t <b ,\\ {f}^{n-2}([c,d]),& t=b ,\end{array}\right.
$$即$N(f^n)=3,n=3,4,\cdots $.
最后,结合(v)和(vii)可以得到情况(viii)的证明.
定理2.5 令$f\in{\cal S}(I,I)$具有形式(1.1),其中$f_1,f_2$严格递减.
(i) 若 $f(a)\neq b$ (或$f(b)\neq a)$ 且 $f(a)>t_0 \geq \max\{f(c),d\},$则$N(f^n)(n\rightarrow\infty)$有界;
(ii) 若 $f(a)\neq b$ (或$f(b)\neq a)$ 且 $\min\{f(d),c\}\geq t_0 >f(b),$则$N(f^n)(n\rightarrow\infty)$有界;
(iii) 若 $b>f(a)>t_0 >f(b)$ (或$f(a)>t_0 >f(b)>a)$ 且 $f(d)\geq t_0 \geq f(c),$则$N(f^n)(n\rightarrow\infty)$有界.
证 情况(i),不失一般性,我们假设$f(a)\neq b$ ($f(b)\neq a$可以类似进行讨论).因$f(a)>t_0 >c$,必存在唯一的点$a_1 \in(a,t_0)$满足$f(a_1)=t_0.$ 显然$a_1$是$f^2$的集值点. 如果存在另一点$b_1\in(t_0,b)$使得$f(b_1)=a_1,$ 则 $f^3$有三个集值点$a_1,t_0,b_1$ (否则,其讨论类似于定理2.4中的情况(v),有$N(f^n)=2,n=2,3,\cdots ).$ 类似地,如果存在$a_2\in(a,a_1)$使得$f(a_2)=b_1,$ 则$f^4$存在四个集值点$a_2,a_1,t_0,b_1$(否则,$N(f^n)=3,n=3,4,\cdots ).$ 重复这个过程,必存在一个有限的正整数$j,$ 有
$$a_j <\cdots <a_2<a_1 <t_0 <b_1 <b_2 <\cdots <b_j .
$$使得$f(b_i)=a_i,\ f(a_{i})=b_{i-1}\ (i=1,2,\cdots ,j)$. 同时注意到$f(a)\neq b$可以导出$f(a_{j+1})\neq b_j,$由此证明了$N(f^n) (n\rightarrow\infty)$的有界性.
情况(ii)-(iii)的证明与(i)类似.
定理2.6 令$f\in{\cal S}(I,I)$具有形式(1.1),其中$f_1,f_2$严格递减.
(i) 若 $f(c)>t_0>c,$则$\lim\limits_{n\rightarrow\infty}N(f^n)=\infty$;
(ii) 若 $d>t_0 >f(d),$则$\lim\limits_{n\rightarrow\infty}N(f^n)=\infty$;
(iii) 若 $f(a)=b,\ f(b)=a,$则$\lim\limits_{n\rightarrow\infty}N(f^n)=\infty.$
证 情况(i),条件$f(c)>t_0>c$及$f_1$严格单减表明$f(a)>t_0$,则必存在$c_1\in(a,t_0)$使得$f(c_1)=t_0.$ 因而必存在另外一点$c_2\in(c_1,t_0)$满足$f(c_2)=c_1.$ 如此下去,我们归纳地得到一个无穷数列
$$\{c_n\}:\ c_1 <c_3 <\cdots <c_{2m+1}<\cdots <c_{2m}<\cdots <c_4 <c_2,
$$满足
$$f(c_{i+1})=c_i ,~~ i=1,2,\cdots .
$$ 显然,当迭代次数$n\rightarrow\infty$时,数列中的点都是$f^n$的集值点,即$\lim\limits_{n\rightarrow\infty}N(f^n)=\infty.$
情况(ii)的证明类似于(i).
对情况(iii),我们分为下面三种讨论:
$$({\rm iii-i})\ d\leq t_0;\ \ ({\rm iii-ii})\ c\geq t_0;\ \ ({\rm iii-iii})\ c<t_0<d.
$$首先考虑$({\rm iii-i}).$ 由假设$f(a)=b>t_0$ 和 $f({t_0}^-)<d\leq t_0,$ 必得到唯一的$d_1\in(a,t_0)$满足$f(d_1)=t_0.$ 由于$f([d_1,t_0))\cup f((t_0,b])$ 覆盖区间 $(a,t_0),$必存在 $d_2\in (d_1,t_0)$ (或 $(t_0,b)$)使得 $f(d_2)=d_1.$ 若$d_2\in (d_1,t_0),$ 则
$$f(d_1)=t_0>d_2,~~ f(d_2)=d_1<d_2,
$$ 说明存在 $d_3\in(d_1,d_2)$满足$f(d_3)=d_2.$ 若 $d_2\in (t_0,b),$ 注意到$f([a,d_1))$覆盖区间$(t_0,b]$,说明存在$d_3\in(a,d_1)$满足$f(d_3)=d_2.$ 如此下去,我们归纳地得到一个无穷数列$\{d_m\}$满足$f(d_1)=t_0$和$f(d_{m+1})=d_m ,m=1,2,\cdots $ 于是极限$\lim\limits_{n\rightarrow\infty}N(f^n)=\infty$得证.情况(iii-ii)-(iii-iii)的证明与(iii-i)类似.
2.3 $f_1$ 严格递增,$f_2$ 严格递减
定理2.7 令$f\in{\cal S}(I,I)$具有形式(1.1),其中$f_1$严格递增,$f_2$严格递减.
(i) 若 $d\leq t_0$ (或$t_0 <\min\{f(a),f(b)\}),$则对任意的整数$n\geq1$有$N(f^n)=1$;
(ii) 若 $c\leq t_0 <f(b),$则对任意的整数$n\geq1$有$N(f^n)=1$;
(iii) 若 $\min\{f(a),f(b)\}=t_0 <\max\{f(a),f(b)\}$ (或$c\leq t_0 =f(b)),$则对任意的整数$n\geq2$有$N(f^n)=2$;
(iv) 若 $c\leq t_0 \leq f(d),\ f(b)<t_0$ (或$f(b)<t_0 <f(a),\ t_0 \leq f(d)),$则对任意的整数$n\geq2$有$N(f^n)=2$;
(v) 若 $f(a)=f(b)=t_0$ (或$f(b)<t_0 =f(a),\ t_0\leq f(d)),$则对任意的整数$n\geq2$有$N(f^n)=3.$
证 由给定的条件,迭代公式(2.2) (或(2.3)) 对情况 (i),迭代公式 (2.1)对情况(ii)仍然保持成立,这说明$N(f^n)=1,n=1,2,\cdots $.
表3
Table 3
表3(Table 3)

表3 $f_1$ 严格递增, $f_2$ 严格递减, 其中 $F$, $G$ 是正整数
|
表3 $f_1$ 严格递增, $f_2$ 严格递减, 其中 $F$, $G$ 是正整数
|
情况(iii),条件$\max\{f(a),f(b)\}>t_0 =\min\{f(a),f(b)\}$ (或 $ c\leq t_0 =f(b))$ 表明迭代公式(2.4) 或 (2.5)(或
$$f^n (t)=\left\{\begin{array}{ll}{f_1}^{n}(t),& a\leq t < t_0,\\f^{n-1}([c,d]),~~& t=t_0,\\{f_2}^n (t),& t_0 < t < b,\\f^{n-2}([c,d]),&t=b\end{array}\right.~)
$$成立,其中$n\geq 2$. 因此$N(f^n)=2,n=2,3,\cdots $.
情况(iv),条件$f(d)\geq t_0 \geq c,\ t_0 >f(b)$ (或 $f(b)<t_0 <f(a),\ t_0 \leq f(d))$说明对任意的$n\geq2$迭代公式 (2.9)(或
$$f^n (t)=\left\{\begin{array}{ll}{f_2}^{n-1} \circ f_1 (t),& a\leq t < t_0,\\{f}^{n-1}([c,d]),& t=t_0,\\{f_2}^{n} (t),& t_0 <t<\breve{t}_0,\\{f}^{n-2}([c,d]),& t=\breve{t}_0,\\{f_2}^{n-2} \circ f_1 \circ f_2 (t),~~ & \breve{t}_0 < t \leq b\end{array}\right.\ \ \ \breve{t}_0 \in(t_0,b) )
$$成立,其中$f(\breve{t}_0)=t_0$. 情况(iv)得证.
类似于定理2.4中(vi)的讨论,能够得到情况(v)的证明.
定理2.8 令$f\in{\cal S}(I,I)$具有形式(1.1),其中$f_1$严格递增,$f_2$严格递减.若$f(a)<t_0 <c,\ t_0\leq f(d)$ 且$f$ 在$[a,t_0)$无不动点,则$N(f^n)(n\rightarrow\infty)$有界.
证 若$f(b)\geq t_0$,条件$f(a)<t_0<c$说明存在唯一的点$r_1 \in(a,t_0)$满足$f(r_1)=t_0.$ 由于$f(t)>t,t\in[a,t_0),$ 我们能够归纳地得到有限个点$a<r_k <r_{k-1}<\cdots <r_2 <r_1 <t_0$满足$f(r_{i+1})=r_i ,i=1,2,\cdots k-1$和$f(a)> r_k.$ 因此,对任意的整数$n\geq k+1$,点$t_0,r_1,r_2,\cdots ,r_k$都是$f^n$的集值点(若$f(b)=t_0,b$ 也是集值点),这证明了$N(f^n)(n\rightarrow\infty)$的有界性.
若 $f(b)< t_0$,对子区间$[a,t_0)$上这些有界集值点的讨论同上.另一子区间$[t_0 ,b]$的讨论类似于定理2.5中情况(ii).
定理2.9 令$f\in{\cal S}(I,I)$具有形式(1.1),其中$f_1$严格递增,$f_2$严格递减.
(i) 若 $f(d)<t_0<d,$ 则 $\lim\limits_{n\rightarrow\infty}N(f^n)=\infty$;
(ii) 若 $f$在$[a,t_0)$存在不动点且$t_0 <c,$则$\lim\limits_{n\rightarrow\infty}N(f^n)=\infty.$
证 =情况(i)的证明与定理 2.6中的(ii)类似,情况(ii)的证明与定理2.3中的(ii)类似. 得证.
2.4 $f_1$ 严格递减,$f_2$ 严格递增
表4
Table 4
表4(Table 4)

表4 $f_1$ 严格递减, $f_2$ 严格递增,其中 $H,$ $I$ 是正整数
|
表4 $f_1$ 严格递减, $f_2$ 严格递增,其中 $H,$ $I$ 是正整数
|
定理2.10 令$f\in{\cal S}(I,I)$具有形式(1.1),其中$f_1$严格递减,$f_2$严格递增.
(i) 若 $t_0 >\max\{f(a),f(b)\}$ (或$c\geq t_0),$则对任意的整数$n\geq1$有$N(f^n)=1$;
(ii) 若 $d\geq t_0 >f(a),$则对任意的整数$n\geq1$有$N(f^n)=1$;
(iii) 若$f(a)>t_0 \geq f(c),d\geq t_0$ (或$f(a)>t_0 >f(b),\ t_0 \geq f(c)),$则对任意的整数$n\geq2$有$N(f^n)=2$;
(iv) 若$\max\{f(a),f(b)\}=t_0 >\min\{f(a),f(b)\}$ (或$d\geq t_0=f(a)),$则对任意的整数$n\geq2$有$N(f^n)=2$;
(v) 若$f(a)=f(b)=t_0$ (或$f(a)>t_0 =f(b),\ t_0 \geq f(c)),$则对任意的整数$n\geq2$有$N(f^n)=3.$
证 情况(i),我们注意到条件 $t_0 >\max\{f(a),f(b)\}$ (或 $c\geq t_0)$可以直接导出 (2.2)式 (或(2.3)式),情况(ii)中的条件$d\geq t_0 >f(a)$可以直接导出(2.1)式,所以$N(f^n)=1,n=1,2,\cdots $.
情况(iii),条件 $f(a)>t_0\geq f(c),d\geq t_0$ (或 $f(a)>t_0 >f(b),\ t_0 \geq f(c))$ 表明 (2.10)式(或
$$f^n (t)=\left\{\begin{array}{ll}{f_1}^{n-2} \circ f_2 \circ f_1 (t),~~& a\leq t <\grave{t}_0,\\{f}^{n-2}([c,d]),& t=\grave{t}_0,\\{f_1}^{n} (t),& \grave{t}_0< t<t_0,\\{f}^{n-2}([c,d]),& t=t_0,\\{f_1}^{n-1} \circ f_2 (t),& t_0 < t \leq b,\end{array}\right.\ \ \grave{t}_0 \in(a,t_0)~)
$$对任意的整数$n\geq2$成立,其中$f(\grave{t}_0)=t_0$. 情况(iii)得证.
情况(iv)-(v) 的证明与定理2.4的(iii)-(vi)类似.
定理2.11 令$f\in{\cal S}(I,I)$具有形式(1.1),其中$f_1$严格递减,$f_2$严格递增.若 $f(c)\leq t_0<f(b)$且$f$在$(t_0,b]$无不动点,则$N(f^n)(n\rightarrow\infty)$无界.
证 其证明类似于定理2.8.
定理2.12 令$f\in{\cal S}(I,I)$具有形式(1.1),其中$f_1$严格递减,$f_2$严格递增.
(i) 若 $f(c)>t_0>c,$ 则$\lim\limits_{n\rightarrow\infty}N(f^n)=\infty$;
(ii) 若$f$在$(t_0,b]$存在不动点且$t_0>d,$则$\lim\limits_{n\rightarrow\infty}N(f^n)=\infty.$
证 情况(i)的证明类似于定理2.6的(i),情况(ii)的证明类似于定理2.3的(i).
3 注记与例子
对于形如(1.1)的USC集值函数,定理2.1-2.12完整地回答了$N(f^n)(n\rightarrow\infty)$的趋向问题. 事实上,我们的方法适用于含有限多个集值点的USC函数迭代问题,同样也适用于定义在整个实数域上的这类集值函数.我们利用下面的例子阐明.
例3.1 考虑上半连续的集值函数${{\phi }_{1}}:[0, 1]\to {{2}^{[0, 1]}}$,定义如下
$$\phi_1 (t)=\left\{\begin{array}{ll} f_1(t),& t\in[0,\frac{1}{5}),\\[3mm] {[\frac{3}{10},\frac{4}{5}],}~~& t=\frac{1}{5},\\[3mm] f_2(t),& t\in(\frac{1}{5},\frac{9}{10}),\\[3mm]{ [\frac{2}{5},\frac{7}{10}],}& t=\frac{9}{10},\\[3mm] f_3(t),& t\in(\frac{9}{10},1],\end{array}\right.
$$ 其中
$${{f}_{1}}(t):=-\frac{3}{2}t+\frac{3}{5},\ \ \ {{f}_{2}}(t):=-\frac{4}{7}t+\frac{32}{35},\ \ {{f}_{3}}(t)):=t-\frac{1}{5}.
$$显然,$\phi_1$含两个集值点$t_1 =\frac{1}{5}$ 和 $ t_2 =\frac{9}{10}.$注意到$\phi_1 ([0, 1])\subset(\frac{1}{5},\frac{9}{10}),$运用定理2.4中(i)和定理2.10的讨论方法,我们得到
|
$\begin{eqnarray}{\phi_1}^n (t)=\left\{\begin{array}{ll} {f_2}^{n-1}\circ f_1 (t),& 0\leq t < \frac{1}{5},\\[3mm] {\phi_1}^{n-1}([\frac{3}{10},\frac{4}{5}]),~~& t=\frac{1}{5},\\[3mm] {f_2}^n (t),& \frac{1}{5} < t < \frac{9}{10},\\[3mm] {\phi_1}^{n-1}([\frac{2}{5},\frac{7}{10}]),& t=\frac{9}{10},\\[3mm] {f_2}^{n-1}\circ f_3 (t),& \frac{9}{10} < t \leq 1,\end{array}\right.\label{examle11}\end{eqnarray}$
|
(3.1)
|
其中$n\geq1.$因此,$N({\phi_1}^n)\equiv N(\phi_1)=2,n=1,2,\cdots $.
例3.2 考虑上半连续的集值函数${{\phi }_{2}}:[0,1]\to {{2}^{[0,1]}},$ 定义如下
$$\phi_2 (t)=\left\{\begin{array}{ll} g_1(t),& t\in[0,\frac{1}{10}), \\[3mm] {[\frac{3}{10},\frac{2}{5}],}~~& t=\frac{1}{10}, \\[3mm] g_2(t),& t\in(\frac{1}{10},\frac{1}{4}), \\[3mm] { [\frac{3}{5},\frac{4}{5}],}& t=\frac{1}{4}, \\[3mm] g_3(t),& t\in(\frac{1}{4},1],\end{array}\right.
$$ 其中
$${{g}_{1}}(t):=\frac{5}{2}t+\frac{1}{20},\ \ \ {{g}_{2}}(t):=\frac{4}{3}t+\frac{4}{15},\ \ {{g}_{3}}(t):=\frac{2}{15}t+\frac{23}{30}.
$$显然, $\phi_2$ 有两个集值点$t_1=\frac{1}{10},\ t_2=\frac{1}{4}.$ 因为$\phi_2$在子区间$[0,\frac{1}{10})\cup(\frac{1}{10},\frac{1}{4})$上无不动点且$\frac{3}{10}>\frac{1}{10}>\frac{1}{20},\ \frac{3}{5}>\frac{1}{4}>\frac{2}{5},$运用定理2.2中(ii)的讨论方法, 我们得到$N({\phi_2}^n)(n\rightarrow\infty)$的有界性.
例3.3 考虑上半连续的集值函数$\phi_3 :(-\infty,\infty)\rightarrow 2^{(-\infty,\infty)},$ 定义如下
$$\phi_3 (t)=\left\{\begin{array}{ll} h_1(t),~~& t\in(-\infty,1), \\{[2,4],}& t=1, \\ h_2(t),& t\in(1,3), \\{[0,1],}& t=3, \\ h_3(t), & t\in(3,\infty),\end{array}\right.
$$ 其中
$${{h}_{1}}(t):=2-{{(t-1)}^{2}},\ \ \ {{h}_{2}}(t):=-2t+6,\ \ {{h}_{3}}(t):=t-2.
$$明显地, $\phi_3$有两个集值点$t_1=1,\ t_2=3.$ 运用定理2.9中(ii)的方法,得到一个无穷数列$\{\xi_n\}$满足
$$h_1 (\xi_1)=1,\ h_1 (\xi_{n+1})=\xi_n , n\geq1.
$$因此, $N({\phi_3}^n)$关于$n$严格递增且$\lim\limits_{n\!\rightarrow\!\infty} N({\phi_3}^n)\!=\!\infty.$
 2016, Vol. 36
2016, Vol. 36  Issue (2): 231-243
Issue (2): 231-243