引言
弥散张量成像(diffusion tensor imagine,DTI)是目前唯一能对脑内纤维进行活体成像的技术,主要通过水分子在人脑内不同方向的弥散速率差异来获取大脑白质纤维束的走向信息[1,2].其中的难题在于如何根据获得的水分子运动信息对神经纤维进行准确的追踪.对此,学者们提出了许多脑白质纤维追踪算法.这些算法根据追踪方式不同可分为确定型[3,4]以及概率型两大类[5,6],确定型主要包括流线型纤维追踪算法(Streamline Tracking,STT)、纤维联络连续追踪算法(Fiber Assignment by Continuous Tracking,FACT)[7]、张量偏转算法(Tensor Deflection,TEND)[8]、多纤维联络连续跟踪(Multiple Fiber Assignment by Continuous Tracking,mFACT)[9]、基于流场分布的纤维追踪算法(Fiber Re-Tracking Based on Flow Field Distribution,FR-Tract)[10]、受限解剖学纤维追踪(Anatomically-Constrained Tractography,ACT)等[11],概率型主要包括纤维方向分布追踪算法(2nd-order Integration over Fibre Orientation Distributions,iFOD2)、粒子滤波追踪算法(Particle Filtering Tractography,PFT)、无迹卡尔曼滤波追踪算法(Unscented Kalman Filter,UKF)等[12,13].
STT算法与FACT算法是最常见的确定型追踪算法.但在使用FACT算法进行纤维束追踪时,不会在体素内进行插值,最后追踪出来的纤维束不符合实际情况,且追踪的准确度不高[9,16],因此在进行纤维追踪时通常是使用STT算法.STT算法通常根据单个体素点的纤维方向分布函数(Orientation Distribution Function,ODF)来对纤维的走向进行估计,未考虑相邻水分子间弥散作用的相互影响,因而鲁棒性较差,追踪结果中也会出现较多的错误纤维.使用适当的方法对重建ODF峰值进行方向修正能解决这一问题[17].近年来,Garyfallidis等人[18]提出了一种改良的确定型纤维追踪算法EuDX,该算法假设体素维度在所有三维中都相等,并对不具有各向同性体素大小的数据进行预处理,在低角度交叉纤维的追踪上有着较好的效果,但追踪时间较长.同时,在进行纤维追踪前还需对种子点区域进行确定,现在常用的种子点选择方法是由Ben等[19]提出的,认为种子点可以从所有白质体素中选择,也可以在灰质与白质的交界处进行选择.因此,在进行全脑追踪时,可以将白质区域的所有体素作为追踪起始点,以保证最后追踪到的纤维束能尽可能覆盖整个白质区域.在后续的研究中[20],有研究者提出使用白质所有体素点进行全脑纤维追踪时区域种子点的数量过大,这样虽然能尽可能多地追踪纤维束从而形成最佳纤维,但同时也导致了假阳性纤维过多以及追踪时间过长等问题.而将灰质与白质交界处体素作为追踪起始点虽然可以减少假阳性纤维的产生,但可能会导致追踪提前终止使得最后追踪到的纤维束无法覆盖所有白质区域.针对这一问题,可对白质区域的所有体素点进行聚类,提取出其中各向异性弥散程度大的点进行追踪,从而在保证纤维束覆盖白质区域的同时减少假阳性纤维的生成.
针对上述方向修正和种子点选取的问题,本文对传统STT算法进行改进,提出一种结合最大期望聚类与最大余弦相似的EM-MSTT(Expectation-Maximization Modified Streamlines Tracking)算法.为验证EM-MSTT算法在纤维追踪上的效果,将使用Fibercup模拟纤维数据、Stanford大学公开的真实脑部数据集以及ISMRM挑战赛2015年公开的模拟脑部数据,并结合恒定立体角(Constant Solid Angle,CSA)模型进行定性以及定量评估.
1 实验部分
1.1 数据和评估方法
1.1.1 实验数据
在本实验中,主要使用三个数据集对算法的有效性和稳定性进行验证.
(1)ISMRM2015年公开模拟脑部数据集
(2)Stanford HARDI数据集
Stanford HARDI数据集是真实脑部数据,由GE Discovery MR750设备扫描得到,扫描参数为:扫描体素量为81×106×76,体素大小为2 mm×2 mm×2 mm,具有150个梯度方向,弥散敏感因子b=2 000 s/mm2. 同时还包含10个b=0的图像.因Stanford HARDI数据集为真实脑部数据,无对应金标准,在本实验中将使用Stanford HARDI数据集进行定性评估[26],验证算法在真实脑部数据上的纤维追踪效果.
(3)Fibercup数据集
Fibercup数据集是2009年MICCA挑战赛上的公开模拟数据集,体素量为64×64×3,体素大小为3 mm ×3 mm×3 mm,具有30个梯度方向,弥散敏感因子b=650 s/mm2.Fibercup数据集由三层相同的纤维结构组成,数据量小,能够快速得到纤维追踪的结果.在实验中主要用于验证本文提出的影响系数的有效性.
因为Stanford HARDI数据集为真实脑部数据集,在进行整体算法的定性评估时能更好的验证追踪算法在实际情况和复杂纤维结构情况下的追踪效果,因此在后续整体算法的定性评估中将只对Stanford HARDI数据集的追踪结果进行展示.
1.1.2 评估方法
在大脑纤维追踪效果的评估中,部分指标较难进行量化评价,如纤维束形态、纤维冗杂程度等.而定性可以弥补这些无法进行量化描述指标的评价,将定性评估和定量评估相结合能得到更为准确的测定结果.为验证本文提出EM-MSTT算法具有较好的追踪效果,将分别使用传统STT算法、EM-MSTT算法以及EuDX算法对ISMRM2015年公开数据集以及Stanford HARDI真实脑部数据集进行纤维追踪,并对追踪结果进行定量以及定性的评估.ISMRM2015挑战赛数据中,在解剖下有25个真实纤维簇,每个具有两个端点区域,共有1 275个可能的端点区域组合.将25个正确追踪纤维簇从组合中取出,保留1 250个错误纤维簇.在定量评估中,针对25个正确纤维簇和1 250个错误纤维簇,将对错误追踪纤维簇数量(Invalid Bundles,IB)、正确追踪纤维簇数量(Valid Bundles,VB)、错误追踪纤维束比率(Invalid Connection,IC)、正确追踪纤维束比率(Valid Connection,VC)、纤维平均重叠率(Mean_Overlap,OL)和纤维平均过度估计率(Mean_Overreach,OR)6个参数进行评估.各参数定义如表1所示.
表1 各评估参数的定义
Table 1
| 评估参数 | 参数定义 |
|---|---|
| IB | 至少有一条追踪纤维束的错误纤维簇数量 |
| VB | 至少有一条追踪纤维束的正确纤维簇数量 |
| IC | IB中的流线数量与追踪到的总的流线数量的比值 |
| VC | VB中的流线数量与追踪到的总的流线数量的比值 |
| OL | VB中的流线在真实纤维束中的体素数量与真实纤维束内体素总数的比值 |
| OR | VB中的流线在真实纤维束之外的体素数量与真实纤维束内体素总数的比值 |
在本次评估实验中,将利用ISMRM2015数据集进行针对全脑的定性评估以及针对全脑和25个不同的特定纤维束的定量评估.同时将利用Stanford HARDI数据集进行针对胼胝体的定性评估.
除此之外,为了评估算法效率,还将从平均纤维束长度以及追踪时间两个方面对ISMRM2015公开数据集进行纤维追踪的定量评估.所用设备为Intel(R) Core(TM) i7-9750H CPU @2.60 GHz,2.59 GHz,最后取3次实验的平均值作为评估结果.
1.2 纤维追踪方法
1.2.1 方向修正算法
在使用传统STT算法对纤维束进行追踪时,通常未考虑水分子间弥散作用的相互影响[10],追踪出的纤维束存在一定的方向偏差,且存在较多的假阳性纤维束.并且在进行纤维束追踪时,若当前体素点为纤维束复杂结构区域,即存在交叉、分叉等情况时,则有可能出现追踪方向错误的情况,这是因为传统算法在进行纤维追踪时,通常是根据ODF峰值将具有相似方向的体素点放入同一矩阵中,然后再使用流线对其进行连接.同时,传统STT算法在进行整条纤维束的追踪时是分别在体素点ODF峰值的正反方向进行追踪然后进行拼接完成的,这导致在复杂纤维结构区域极易出现错误的追踪.针对这一问题,本文提出了一种方向修正算法对纤维束追踪方向进行修正,使追踪纤维走向更符合实际,同时一定程度上可减少假阳性纤维的生成.
本文算法在体素点正反方向纤维束进行拼接时对偏转方向θ进行判定,设在体素点a处正方向追踪纤维束体素点矩阵为
其中concatenate表示将括号中两矩阵进行连接,
除此之外,还将考虑水分子间弥散作用的相互影响对体素点ODF次峰值进行修正,因ODF重建是在以当前体素点为原点的球面坐标系中进行,因此可假设修正方向、主方向(最大弥散方向)、次方向(次峰值方向)处于同一平面内,可建立以下平面方程:
在ODF球面坐标系中,因方向向量的起点均为当前体素点,因此当前体素点包含在所求平面中,可假设当前体素点坐标为
同时设
其中β为水分子间弥散的影响系数,经过多次实验迭代取最优值,在本实验中
在实验时为减少追踪过程中短纤维的生成,提高追踪准确率,将对追踪纤维进行筛选,将5 mm以上长度的纤维作为追踪结果.
1.2.2 种子点筛选算法
为解STT算法在进行全脑追踪时种子点过多导致假阳性纤维增多的问题,本文在STT算法的基础上,加入EM(Expectation Maximization)聚类对种子点进行聚类提取.EM聚类算法将初始种子点的弥散强度系数作为特征并对其进行聚类,将初始种子点大致分为椭球形弥散、盘形弥散和球形弥散3类[9],其中椭球形弥散的种子点表现为强各向异性弥散.之后将椭球形弥散类簇中的种子点作为新种子点进行追踪,由于纤维束内的水分子基本都为椭球形弥散,使用聚类后的种子点进行追踪能使结果更符合实际情况下的纤维分布,并且能较大程度的减少假阳性纤维的产生.
EM聚类算法,是一种估计隐变量的聚类方法,主要是分E-M两步交替进行的.
E步骤:
在E步骤中主要是根据数据点的特征参数计算其属于某一类的概率,并将该概率作为所属类别的权重.而当某一数据点在两类别具有相同权重时,该数据点属于两个类簇.因此EM算法没有规定一个数据点只能属于一个类别,这也是EM算法的软聚类特性.
在本次实验中,通过扫描数据计算得到各体素点的3个特征值
因每个体素点存在3个特征参数,将使用相似度度量方法将所有体素点聚类为3类——椭球形弥散体素点、盘形弥散体素点、球形弥散体素点.欧氏距离和余弦相似度是最常见的相似度度量方法.若将弥散强度看作是三维空间坐标系中一个点的坐标值(x, y, z),欧氏距离是衡量两点之间的绝对距离,主要是体现个体之间数值的绝对差异.而余弦相似度对绝对数值不太敏感,主要是对两数据之间的相似程度进行判定,属于一种定性的度量[27].在使用弥散强度系数对体素点进行聚类时,主要判断体素点与聚类中心的相似程度而不是数值上的绝对差异,因此在实验中将选取余弦相似度作为度量方式进行聚类,将所有体素点分为椭球形弥散体素点、盘形弥散体素点、球形弥散体素点3类,之后再进行纤维追踪.在使用余弦相似度对相似程度进行度量时,需保证各数据处于相同的刻度级别下,因此在进行聚类前还需对数据进行标准化处理,避免因刻度级别不同而带来的偏差.将弥散强度看作是三维空间坐标系中一个点的坐标值(x, y, z)来进行余弦相似度判断,针对体素点
权重
M步骤:
M步骤主要利用上一步中聚类完成后各数据点的特征数据更新聚类中心[13].在对纤维进行追踪时主要对象是呈椭球形弥散的体素点,因此将
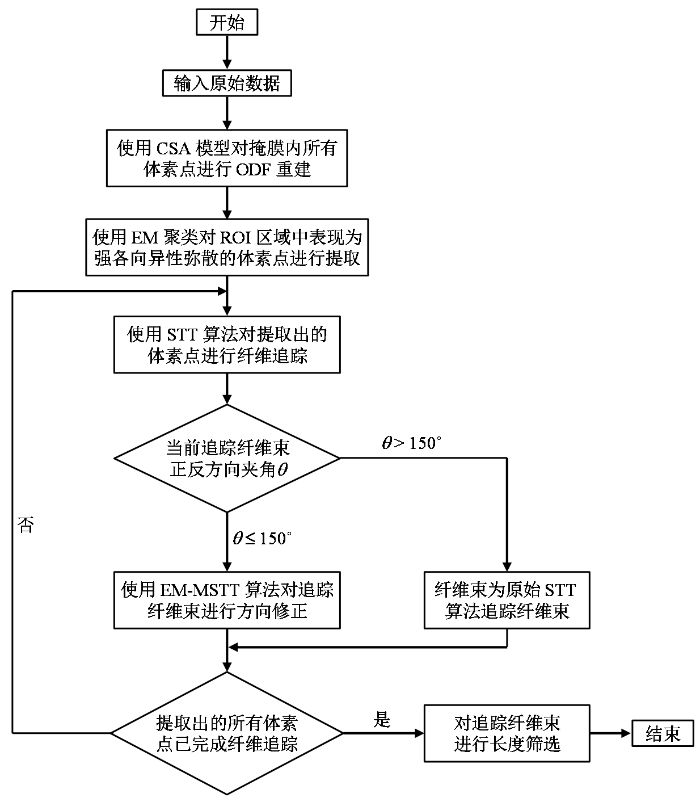
算法EM-MSTT具体流程如图1所示.
图1
2 结果与讨论
2.1 实验结果
2.1.1 ISMRM数据集实验结果
在对ISMRM中的数据进行聚类操作时,将各体素点的弥散强度作为三维空间坐标.在ISMRM数据集中,ROI区域内总共有59 000个体素点,考虑到数据分布以及聚类收敛的问题,体素点特征保留到小数点后两位,若出现特征重复的情况可作权重值处理,但由于数据分布在边界的极值点较多,在考虑数据权重时可能会对聚类结果造成较大误差.因拟合会花费较多时间,为在减少因极值点与权重原因造成误差的同时节省实验时间,将把传统STT算法与有极值无权重、有极值有权重、无极值有权重、无极值无权重4种条件下的EM-STT算法(只进行聚类优化不进行方向修正的STT算法)进行比较,并选取其中追踪效果最好的情况下对应的条件作为后续EM-MSTT算法的聚类条件,经过实验发现,无权重条件下的追踪结果均优于有权重条件下的结果,在无权重条件下,不考虑极值时正确的纤维追踪比率高于考虑极值情况下的追踪比率,并且追踪到的错误纤维束相较于考虑极值时还有所减少.因此在本次实验中将选择无权重不考虑极值作为聚类条件对种子点进行聚类,之后再对EM-MSTT算法(同时进行种子点聚类和方向修正)、MSTT算法(只进行方向修正)、EM-STT算法(只进行种子点聚类)、传统STT算法以及EuDX算法的追踪结果进行对比,以验证本文提出方法的有效性.除此之外,还将针对25个不同纤维簇比较EM-MSTT算法、传统STT算法和EuDX算法追踪的重叠率和过度估计率.不同算法的评估参数如表2所示,EM-MSTT算法、传统STT算法和EuDX算法在不同纤维素上的重叠率和过度估计率,以及纤维追踪效率分别如 表3、表4和表5所示.3种算法对ISMRM数据集的定性评估结果如图2所示.
表2 不同算法追踪评估参数结果对比
Table 2
| 算法(均以CSA为重建模型) | IB/簇 | VB/簇 | IC/% | VC/% | OL/% | OR/% |
|---|---|---|---|---|---|---|
| 传统STT算法 | 92 | 22 | 25.45 | 22.94 | 55.08 | 15.68 |
| EuDX算法 | 181 | 22 | 40.01 | 29.83 | 45.20 | 46.46 |
| MSTT算法 | 73 | 22 | 34.75 | 30.45 | 57.11 | 10.70 |
| EM-STT算法 | 64 | 22 | 38.14 | 43.95 | 61.97 | 6.11 |
| EM-MSTT算法 | 50 | 22 | 40.00 | 45.39 | 60.57 | 4.62 |
注:金标准中VB数量为25簇.
表3 EM-MSTT算法、EuDX算法和STT算法在不同纤维簇上的纤维平均重叠率
Table 3
| 纤维簇 | OLEM-MSTT/% | OLEuDX/% | OLSTT/% |
|---|---|---|---|
| CA | 0 | 0 | 0 |
| CC | 73.839 | 48.743 | 66.066 |
| Cingulum_left | 68.209 | 64.403 | 65.309 |
| Cingulum_right | 68.915 | 54.019 | 60.711 |
| CP | 0 | 0 | 0 |
| CST_left | 55.384 | 15.192 | 86.885 |
| CST_right | 93.041 | 23.954 | 93.159 |
| Fornix | 58.672 | 60.891 | 55.098 |
| FPT_left | 79.141 | 40.277 | 70.873 |
| FPT_right | 78.657 | 69.175 | 63.173 |
| ICP_left | 61.53 | 87.299 | 51.831 |
| ICP_right | 69.382 | 85.118 | 59.593 |
| ILF_left | 70.873 | 92.549 | 64.728 |
| ILF_right | 72.071 | 43.874 | 65.118 |
| MCP | 64.808 | 46.177 | 56.735 |
| OR_left | 66.196 | 49.246 | 62.255 |
| OR_right | 69.757 | 45.066 | 64.938 |
| POPT_left | 75.582 | 51.243 | 67.654 |
| POPT_right | 84.312 | 68.454 | 81.571 |
| SCP_left | 44.862 | 37.176 | 43.26 |
| SCP_right | 59.348 | 45.813 | 57.184 |
| SLF_left | 55.613 | 37.52 | 50.871 |
| SLF_right | 72.212 | 43.055 | 64.282 |
| UF_left | 73.601 | 44.564 | 65.289 |
| UF_right | 74.841 | 46.213 | 68.793 |
注:25个纤维簇主要包含以下纤维结构:CA(前连合)、CC(胼胝体)、Cingulum(扣带回)、CP(后连合)、CST(皮质脊髓束)、Fornix(穹隆)、FPT(额叶)、ICP(小脑下脚)、ILF(下纵束)、MCP(小脑下脚)、OR(视辐射)、POPT(顶枕脑桥束)、SCP(小脑上脚)、SLF(上纵束)、UF(钩束),其中left和right表示纤维簇所在半脑.
表4 EM-MSTT算法、EuDX算法和STT算法在不同纤维簇上的过度估计率
Table 4
| 纤维簇 | OREM-MSTT/% | OREuDX/% | ORSTT/% |
|---|---|---|---|
| CA | 0 | 0 | 0 |
| CC | 16.26 | 91.455 | 33.531 |
| Cingulum_left | 13.853 | 68.95 | 24.478 |
| Cingulum_right | 10.428 | 59.699 | 26.387 |
| CP | 0 | 0 | 0 |
| CST_left | 0.597 | 6.057 | 0.329 |
| CST_right | 0.467 | 7.065 | 0.53 |
| Fornix | 17.991 | 91.711 | 29.334 |
| FPT_left | 3.45 | 32.986 | 6.945 |
| FPT_right | 9.876 | 56.532 | 16.741 |
| ICP_left | 29.943 | 140.771 | 60.037 |
| ICP_right | 20.682 | 129.07 | 44.528 |
| ILF_left | 24.861 | 110.708 | 39.684 |
| ILF_right | 17.411 | 98.978 | 33.422 |
| MCP | 13.203 | 78.426 | 26.03 |
| OR_left | 14.995 | 64.918 | 23.818 |
| OR_right | 13.014 | 79.618 | 24.491 |
| POPT_left | 10.306 | 54.182 | 18.969 |
| POPT_right | 2.481 | 14.867 | 3.065 |
| SCP_left | 49.547 | 122.086 | 63.624 |
| SCP_right | 25.669 | 78.782 | 37.109 |
| SLF_left | 37.496 | 139.848 | 57.985 |
| SLF_right | 14.786 | 109.349 | 32.889 |
| UF_left | 18.773 | 113.686 | 37.099 |
| UF_right | 18.524 | 98.526 | 30.538 |
表5 EM-MSTT算法、EuDX算法和STT算法的效率对比
Table 5
| 算法 | 平均纤维长度/mm | 耗时/s |
|---|---|---|
| EM-MSTT | 74.29 | 46.4 |
| EuDX | 75.96 | 78.66 |
| STT | 45.14 | 3446.65 |
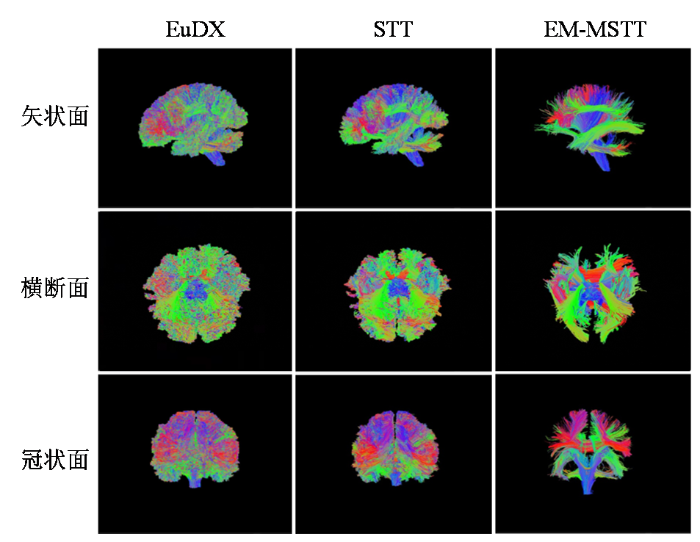
图2
图2
EuDX算法、STT算法和EM-MSTT算法对ISMRM数据集的定性评估结果
Fig. 2
Results of qualitative evaluation of ISMRM dataset by EuDX algorithm, STT algorithm and EM-MSTT algorithm
2.1.2 Stanford HARDI数据集实验结果
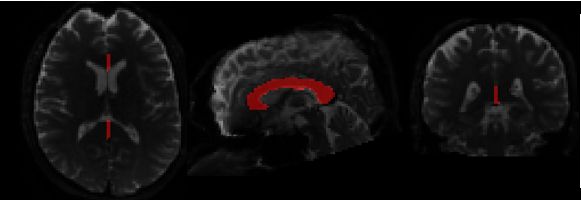
图3
图3
胼胝体ROI区域(红色)选择情况
Fig. 3
Selection of ROI regions (red) in the corpus callosum
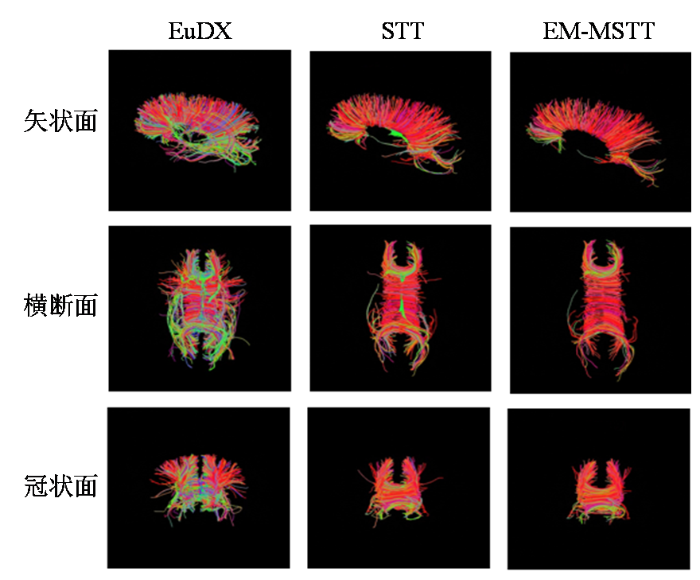
图4
图4
EuDX算法、STT算法和EM-MSTT算法对胼胝体的追踪结果
Fig. 4
Tracking results of EuDX algorithm, STT algorithm and EM-MSTT algorithm for corpus callosum
2.2 讨论
2.2.1 ISMRM数据集结果讨论
从表2可看出,MSTT和EM-STT算法的正确追踪纤维束比率即VC均高于传统STT算法和目前常用的EuDX算法,将MSTT和EM-STT两种算法结合后的EM-MSTT算法的VC远高于传统STT算法与EuDX算法.在进行全脑纤维束追踪时金标准为25簇,各算法都成功追踪到了其中的22簇,但EM-MSTT算法错误追踪纤维束即IB只有50簇,相较于传统STT算法少了42簇,相较于EuDX算法少了131簇,在较大程度上减少了假阳性纤维的产生.同时在正确追踪纤维束比率VC上,EM-MSTT算法比传统STT算法高了22.45%,相较于EuDX算法也提升了15.56%,能更好的对纤维束进行追踪.传统STT纤维追踪算法在进行纤维追踪起始点选择时只考虑了体素点是否在掩膜内而忽略了体素点本身的弥散性质,对各向同性弥散的体素点也进行了追踪,从而导致结果中存在大量的假阳性纤维,同时也忽略了水分子间弥散作用的相互影响,导致追踪结果与实际情况之间存在一定差距.EM-MSTT算法作为一种种子点聚类与方向修正的纤维追踪算法,通过加入合适的相似度度量方法以及方向修正方法,能较好的对各向异性弥散的体素点进行聚类提取,同时也考虑到水分子间弥散作用的相互影响对重建ODF的峰值方向进行修正,从而在纤维追踪中得到更加准确、有效的结果.
在表5的算法效率对比中可以看出,EuDX算法相较于传统STT算法平均纤维长度大幅度提升,且大幅缩短了耗时,EM-MSTT算法则在维持追踪纤维长度与EuDX算法相当的情况下,进一步缩短了纤维追踪所需的时间,这是因为EM-MSTT算法对种子点进行了聚类筛选,减少了无效种子点的数量,从而减少了追踪所需要的时间.因此本文提出的EM-MSTT算法在平均纤维长度和追踪时间上都优于传统STT算法,同时在追踪时间上优于EuDX算法.
从图2中3种算法的追踪结果来看,EuDX算法追踪结果较为杂乱,大脑纤维结构不清晰,且存在较多的假阳性纤维.与EuDX算法相比,传统STT算法能较好的表达大脑纤维结构信息,但依然存在较多的假阳性纤维.相较于EuDX算法与传统STT算法,本文提出的EM-MSTT算法能更加清晰的表达出纤维的连接情况,能更好的展示大脑结构信息,且存在较少的假阳性纤维,在纤维形态结构的研究上能提供较大的帮助.
2.2.2 Stanford HARDI数据集结果讨论
从图4胼胝体追踪结果可以看出,EuDX算法追踪纤维束较为杂乱,同时存在较多的假阳性纤维,传统STT算法追踪到的假阳性纤维束大幅度减少,但在部分复杂纤维结构区域出现了纤维紊乱的情况,而EM-MSTT算法追踪的纤维束更加整洁平滑,且假阳性纤维束较少,追踪出的纤维束也更符合实际分布情况.根据Stanford HARDI数据集追踪结果的定性分析,能看出本文提出算法在真实脑部数据上也有较好的追踪效果.
3 结论
传统确定型纤维追踪算法在进行种子点输入时通常是对ROI区域内的所有体素点进行遍历,然后根据体素点ODF峰值进行纤维追踪,这样会出现种子点过多以及追踪易受到噪声影响的问题,从而导致假阳性纤维的生成.针对这一问题,本文在传统确定型纤维追踪算法的基础上,提出了一种EM-MSTT算法,该算法通过最大余弦相似和最大期望聚类对种子点进行分类,并使用移动最小二乘法对纤维路径进行拟合,从而提高纤维追踪的准确率.之后分别使用ISMRM模拟脑部数据和Stanford大学真实脑部数据对传统STT算法、EM-MSTT算法以及EuDX算法进行了定量和定性的评估,验证了EM-MSTT算法的准确性和有效性.定量评估表明,EM-MSTT算法相较于传统确定型纤维追踪算法能大幅减少假阳性纤维的生成,同时能更准确的对纤维束进行追踪.定性评估表明,通过EM-MSTT算法追踪的纤维束整洁平滑,且更符合实际情况下纤维的分布.但EM-MSTT追踪算法仍存在以下不足:(1)仅对种子点输入以及交叉纤维的追踪进行了优化,在单纤维的追踪上并未作太大改动,因此可能存在方向上的累计误差;(2)在大范围纤维追踪上效果较好,在细微结构的纤维追踪上可能会出现细节丢失的情况.在之后的研究中可进一步对算法的纤维方向选择部分进行改进,提高单纤维体素点方向选择的准确度,同时对聚类部分进行优化,寻找一种适用于细微结构区域纤维追踪的聚类方法.
利益冲突
无
参考文献
A comparison of three fiber tract delineation methods and their impact on white matter analysis
[J].
DOI:S1053-8119(18)30451-8
PMID:29787865
[本文引用: 1]

Diffusion magnetic resonance imaging (dMRI) is an important method for studying white matter connectivity in the brain in vivo in both healthy and clinical populations. Improvements in dMRI tractography algorithms, which reconstruct macroscopic three-dimensional white matter fiber pathways, have allowed for methodological advances in the study of white matter; however, insufficient attention has been paid to comparing post-tractography methods that extract white matter fiber tracts of interest from whole-brain tractography. Here we conduct a comparison of three representative and conceptually distinct approaches to fiber tract delineation: 1) a manual multiple region of interest-based approach, 2) an atlas-based approach, and 3) a groupwise fiber clustering approach, by employing methods that exemplify these approaches to delineate the arcuate fasciculus, the middle longitudinal fasciculus, and the uncinate fasciculus in 10 healthy male subjects. We enable qualitative comparisons across methods, conduct quantitative evaluations of tract volume, tract length, mean fractional anisotropy, and true positive and true negative rates, and report measures of intra-method and inter-method agreement. We discuss methodological similarities and differences between the three approaches and the major advantages and drawbacks of each, and review research and clinical contexts for which each method may be most apposite. Emphasis is given to the means by which different white matter fiber tract delineation approaches may systematically produce variable results, despite utilizing the same input tractography and reliance on similar anatomical knowledge.Copyright © 2018. Published by Elsevier Inc.
SANDI: a compartment-based model for non-invasive apparent soma and neurite imaging by diffusion MRI
[J].
Diffusion MRI in the brain-theory and concepts
[J].
Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging
[J].
DOI:10.1002/1531-8249(199902)45:2<265::aid-ana21>3.0.co;2-3
PMID:9989633
[本文引用: 1]

The relationship between brain structure and complex behavior is governed by large-scale neurocognitive networks. The availability of a noninvasive technique that can visualize the neuronal projections connecting the functional centers should therefore provide new keys to the understanding of brain function. By using high-resolution three-dimensional diffusion magnetic resonance imaging and a newly designed tracking approach, we show that neuronal pathways in the rat brain can be probed in situ. The results are validated through comparison with known anatomical locations of such fibers.
A Bayesian approach for stochastic white matter tractography
[J].
DOI:10.1109/tmi.2006.877093
PMID:16894991
[本文引用: 1]

White matter fiber bundles in the human brain can be located by tracing the local water diffusion in diffusion weighted magnetic resonance imaging (MRI) images. In this paper, a novel Bayesian modeling approach for white matter tractography is presented. The uncertainty associated with estimated white matter fiber paths is investigated, and a method for calculating the probability of a connection between two areas in the brain is introduced. The main merits of the presented methodology are its simple implementation and its ability to handle noise in a theoretically justified way. Theory for estimating global connectivity is also presented, as well as a theorem that facilitates the estimation of the parameters in a constrained tensor model of the local water diffusion profile.
Probabilistic white matter fiber tracking using particle filtering and von Mises-Fisher sampling
[J].
DOI:10.1016/j.media.2008.05.001
PMID:18602332
[本文引用: 1]

Standard particle filtering technique have previously been applied to the problem of fiber tracking by Brun et al. [Brun, A., Bjornemo, M., Kikinis, R., Westin, C.F., 2002. White matter tractography using sequential importance sampling. In: Proceedings of the ISMRM Annual Meeting, p. 1131] and Bjornemo et al. [Bjornemo, M., Brun, A., Kikinis, R., Westin, C.F., 2002. Regularized stochastic white matter tractography using diffusion tensor MRI, In: Proc. MICCAI, pp. 435-442]. However, these previous attempts have not utilised the full power of the technique, and as a result the fiber paths were tracked in a goal directed way. In this paper, we provide an advanced technique by presenting a fast and novel probabilistic method for white matter fiber tracking in diffusion weighted MRI (DWI), which takes advantage of the weighting and resampling mechanism of particle filtering. We formulate fiber tracking using a non-linear state space model which captures both smoothness regularity of the fibers and the uncertainties in the local fiber orientations due to noise and partial volume effects. Global fiber tracking is then posed as a problem of particle filtering. To model the posterior distribution, we classify voxels of the white matter as either prolate or oblate tensors. We then construct the orientation distributions for prolate and oblate tensors separately. Finally, the importance density function for particle filtering is modeled using the von Mises-Fisher distribution on a unit sphere. Fast and efficient sampling is achieved using Ulrich-Wood's simulation algorithm. Given a seed point, the method is able to rapidly locate the globally optimal fiber and also provides a probability map for potential connections. The proposed method is validated and compared to alternative methods both on synthetic data and real-world brain MRI datasets.
Tensorlines: advection diffusion based propagation through diffusion tensor fields
[C]//
White matter tractography using diffusion tensor deflection
[J].Diffusion tensor MRI provides unique directional diffusion information that can be used to estimate the patterns of white matter connectivity in the human brain. In this study, the behavior of an algorithm for white matter tractography is examined. The algorithm, called TEND, uses the entire diffusion tensor to deflect the estimated fiber trajectory. Simulations and imaging experiments on in vivo human brains were performed to investigate the behavior of the tractography algorithm. The simulations show that the deflection term is less sensitive than the major eigenvector to image noise. In the human brain imaging experiments, estimated tracts were generated in corpus callosum, corticospinal tract, internal capsule, corona radiata, superior longitudinal fasciculus, inferior longitudinal fasciculus, fronto-occipital fasciculus, and uncinate fasciculus. This approach is promising for mapping the organizational patterns of white matter in the human brain as well as mapping the relationship between major fiber trajectories and the location and extent of brain lesions.Copyright 2003 Wiley-Liss, Inc.
A multiple streamline approach to high angular resolution diffusion tractography
[J].
Fiber re-tracking based on flow field distribution
[J].
基于流场分布的纤维续跟踪
[J].
Anatomically constrained tractography:improved diffusion MRI streamlines tractography through effective use of anatomical information
[J].
Filtered multitensor tractography
[J].
DOI:10.1109/TMI.2010.2048121
PMID:20805043
[本文引用: 1]

We describe a technique that uses tractography to drive the local fiber model estimation. Existing techniques use independent estimation at each voxel so there is no running knowledge of confidence in the estimated model fit. We formulate fiber tracking as recursive estimation: at each step of tracing the fiber, the current estimate is guided by those previous. To do this we perform tractography within a filter framework and use a discrete mixture of Gaussian tensors to model the signal. Starting from a seed point, each fiber is traced to its termination using an unscented Kalman filter to simultaneously fit the local model to the signal and propagate in the most consistent direction. Despite the presence of noise and uncertainty, this provides a causal estimate of the local structure at each point along the fiber. Using two- and three-fiber models we demonstrate in synthetic experiments that this approach significantly improves the angular resolution at crossings and branchings. In vivo experiments confirm the ability to trace through regions known to contain such crossing and branching while providing inherent path regularization.
Threshold-based brain white matter fiber probability tracking algorithm
[J].
Review of neural fiber tracking with diffusion magnetic resonance imaging
[J].
扩散磁共振图像的神经纤维追踪算法研究综述
[J].扩散磁共振成像是目前唯一非侵入性研究脑神经纤维束微结构的技术,神经纤维追踪技术是显示神经纤维的关键步骤.本文综述了两大类的神经纤维追踪算法的研究进展,即:局部型追踪方法和全局型追踪方法,阐明各个追踪算法的优点以及存在的局限性,然后在此基础上介绍了在神经纤维追踪过程中能做出优化的具体方面,包括局部纤维方向建模、张量插值、种子点的选取、传播方向以及终止准则等,最后对神经纤维追踪算法的未来发展趋势进行展望.
Brain fiber tracking method based on k-means and moving least squares
[J].
结合K-Means与移动最小二乘法的脑部纤维追踪方法
[J].
Automatic removal of false connections in diffusion mri tractography using topology-informed pruning (TIP)
[J].
Fiber-tractography via diffusion tensor MRI (DT-MRI)
[J].
Diffusion MRI fiber tractography of the brain
[J].
DOI:10.1002/nbm.3785
[本文引用: 1]

The ability of fiber tractography to delineate non-invasively the white matter fiber pathways of the brain raises possibilities for clinical applications and offers enormous potential for neuroscience. In the last decade, fiber tracking has become the method of choice to investigate quantitative MRI parameters in specific bundles of white matter. For neurosurgeons, it is quickly becoming an invaluable tool for the planning of surgery, allowing for visualization and localization of important white matter pathways before and even during surgery. Fiber tracking has also claimed a central role in the field of "connectomics," a technique that builds and studies comprehensive maps of the complex network of connections within the brain, and to which significant resources have been allocated worldwide. Despite its unique abilities and exciting applications, fiber tracking is not without controversy, in particular when it comes to its interpretation. As neuroscientists are eager to study the brain's connectivity, the quantification of tractography-derived "connection strengths" between distant brain regions is becoming increasingly popular. However, this practice is often frowned upon by fiber-tracking experts. In light of this controversy, this paper provides an overview of the key concepts of tractography, the technical considerations at play, and the different types of tractography algorithm, as well as the common misconceptions and mistakes that surround them. We also highlight the ongoing challenges related to fiber tracking. While recent methodological developments have vastly increased the biological accuracy of fiber tractograms, one should be aware that, even with state-of-the-art techniques, many issues that severely bias the resulting structural "connectomes" remain unresolved.
Displaying the autonomic processing network in humans-a global tractography approach
[J].
Sparse deconvolution of higher order tensor for fiber orientation distribution estimation
[J].
DOI:10.1016/j.artmed.2015.09.004
PMID:26428956
[本文引用: 1]

Higher order tensor (HOT) imaging approaches based on the spherical deconvolution framework have attracted much interest for their effectiveness in estimating fiber orientation distribution (FOD). However, sparse regularization techniques are still needed to obtain stable FOD in solving the deconvolution problem, particularly in very high orders. Our goal is to adequately characterize the actual sparsity lying in the FOD domain to develop accurate estimation approach for fiber orientation in HOT framework.We propose a sparse HOT regularization model by enforcing the sparse constraint directly on the representation of FOD instead of imposing it on coefficients of basis function. Then, we incorporate both the stabilizing effect of the l2 penalty and the sparsity encouraging effect of the l1 penalty in the sparse model to adequately characterize the actual sparsity lying in the FOD domain. Furthermore, a weighted regularization scheme is developed to iteratively solve the deconvolution problem. The deconvolution technique is compared against existing methods using l2 or l1 regularizer and tested on synthetic data and real human brain.Experiments were conducted on synthetic data and real human brain data. The synthetic experimental results indicate that crossing fibers are more easily detected and the angular resolution limit is improved by our method by approximately 20°-30° compared to existing HOT method. The detection accuracy is considerably improved compared with that of spherical deconvolution approaches using the l2 regularizer and the reweighted l1 scheme.Results of testing the deconvolution technique demonstrate that it allows HOTs to obtain increasingly clean and sharp FOD, which in turn significantly increases the angular resolution of current HOT methods. With sparsity on FOD domain, this method efficiently improves the ability of HOT in resolving crossing fibers.Copyright © 2015 Elsevier B.V. All rights reserved.
Strengths and weaknesses of state of the art fiber tractography pipelines-A comprehensive in vivo and phantom evaluation study using Tractometer
[J].
COMMIT: Convex optimization modeling for microstructure informed tractography
[J].
Author Correction: The challenge of mapping the human connectome based on diffusion tractography
[J].
A fiber tracking algorithm based on non-local constrained spherical deconvolution
[J].
基于非局部约束球面反卷积模型的纤维追踪算法
[J].
Correction: evaluating the accuracy of diffusion MRI models in white matter
[J].
Brain fibre tracking improved by diffusion tensor similarity using non-euclidean distances
[C]//