引言
扩散磁共振成像(Diffusion Magnetic Resonance Imaging,dMRI)是在磁共振基础上发展起来的一项技术,可以通过检测活体组织内水分子的扩散运动状态来反映生物组织的微观结构变化.扩散张量成像(Diffusion Tensor Imaging,DTI)是最早被提出用来估计纤维方向分布的dMRI技术,该技术通过采集不同扩散敏感梯度方向的扩散加权图像进行张量成像,用于描述水分子的自由扩散运动[1].在脑组织中,水分子的自由扩散运动由于细胞器、细胞膜和大分子等结构的限制,使其在三维空间内的各个方向上的扩散速度不同,这种现象被称为各向异性扩散[2].DTI通过检测水分子在大脑中的扩散情况来获取各向异性等信息,能够反映组织结构的微观特征.同时,DTI可根据张量测值的主扩散方向计算得到白质纤维束的路径,是目前非侵入性获得活体白质微观组织结构的唯一手段,具有重要的临床价值[3].
为了提高图像的SNR,临床上通常采取对同一对象进行重复采集并求均值图像的方法,但这种方法较为耗时,可能会增加患者的不适,并导致运动伪影的出现.因此,有效的后处理去噪算法对于DTI去噪至关重要.近年来,DTI去噪领域的研究取得了一些新进展,包括利用深度学习技术训练去噪模型、利用磁共振多模态数据中的冗余信息、联合自监督统计思想和生成模型联合去噪等.以往的综述论文往往从图像域和空间域两大方面对DTI去噪算法进行讨论[6],或者着重于特定算法在DTI去噪中的应用[7].考虑到上述研究进展,本文将DTI去噪方法分为传统图像处理方法与深度学习方法两类,并对每一类方法进行更为详细的分类,同时介绍每类方法中经典算法的优缺点.另外,本文还探讨了生成模型在DTI去噪领域的最新应用,这一方向未来或许会成为该领域新的研究重点.
本文第1节介绍DTI成像原理及噪声分析;第2节从传统图像处理和深度学习两个角度综述经典的DTI去噪方法与最新的研究进展,并讨论这两类方法的优点及其局限性;第3节介绍评估标准及常用公开数据集;第4节讨论文中提及的DTI去噪方法;第5节对本文进行总结并对未来研究方向进行展望.
1 扩散张量成像与噪声分析
1.1 扩散张量成像
扩散加权成像(Diffusion Weighted Imaging,DWI)通过对普通磁共振成像(Magnetic Resonance Imaging,MRI)施加不同方向的扩散敏感梯度脉冲,来检测机体组织中水分子的扩散状态.通过Stejskal-Tanner公式对不同方向上的DWI图像进行计算,可以得到DTI图像.
DTI图像中的每一个体素都是由扩散张量D组成的,D是一个3×3的对称正定矩阵,能够描述人体组织内水分子的扩散运动,表示如下:
(1)式中
其中i表示方向数,
1.2 噪声分析
磁共振的接收线圈在接收磁共振信号的同时,也接收到了因各种因素而产生的噪声.接收信号中所包含的噪声通常表现为零均值的加性高斯噪声,含噪模型表示如下:
其中y为接收信号,s为不含噪的真实信号,n为零均值的加性高斯噪声.
由(2)式可知,DTI图像中的噪声主要来源于DWI图像,每个体素的信号都是由实部和虚部组成的复数信号
其中
其中
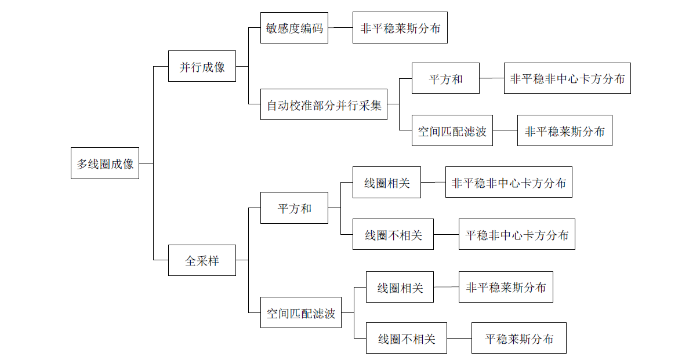
随着多线圈成像技术的发展,成像速度和质量都得到了提高,此时幅值图像中的噪声分布取决于K空间信号采样方式、幅值信号的重建方式及线圈的组合方式[8].对于下采样K空间的并行成像,敏感度编码(Sensitivity Encoding,SENSE)和自动校准部分并行采集(Generalized Autocalibrating Partially Parallel Acquisitions,GRAPPA)是流行的重建方式;对于全采样K空间,平方和(Sum Of Squares,SOS)和空间匹配滤波(Spatial Matched Filter,SMF)是常用的重建方式.此外,噪声分布也受到线圈间相关性的影响,图1总结了多线圈成像中各种类型的噪声.多线圈成像技术获取的幅值图像具有空间平稳或非平稳的莱斯或非中心卡方噪声,其中服从非中心卡方分布的幅值图像可以表示为:
其中c为采集通道数.
图1
需要注意的是,现有多数DTI去噪方法仅针对莱斯噪声,因此在没有特别说明的情况下,本文中提到的噪声均指莱斯噪声.
2 扩散张量图像去噪方法
在过去几十年中,研究者提出了大量有效的DTI去噪算法,旨在从噪声图像中恢复出无噪图像,并保留图像的解剖细节及边缘信息.根据处理的数据对象,他们提出了两种去噪方案:一种是在确定DTI数据之前对DWI数据进行去噪;另一种则是直接处理DTI数据.前者能够产生更好的视觉效果,但其没有考虑DWI多通道之间的信息,这可能导致计算的张量信息存在偏差.后者的处理方式较为直观,但相较于前者却并不合理,因为一旦DTI数据被确定,就无法校正由DWI背景噪声所引起的扩散参数估计偏差.考虑到深度学习的广泛应用,本文将DTI去噪方法分为传统图像处理方法与深度学习方法两类.需要注意的是,尽管本文对这些方法进行了分类,但它们并不完全独立,部分方法之间可能存在关联.
2.1 传统图像处理去噪算法
传统滤波算法包括双边滤波、高斯滤波、中值滤波等,这些方法可以有效去除高斯噪声,但是会导致图像边缘模糊、细节丢失,且不能有效去除复杂的莱斯噪声.为有效去除DTI数据中的复杂噪声且保留图像精细的特征和边缘,研究者已经提出了大量的传统图像处理去噪算法,这些算法大致可以归纳为以下几类:(1)基于非局部均值(Non-Local Means,NLM)的去噪算法.(2)基于主成分分析(Principal Component Analysis,PCA)的去噪算法.(3)基于低秩矩阵近似(Low Rank Matrix Approximation,LRMA)的去噪算法等.
2.1.1 基于非局部均值去噪算法
图像中每个像素点并不是独立于周围像素的,其附近区域通常存在着许多在灰度值和结构上相似的像素点,这种特性称为图像的非局部自相似性(Nonlocal Self-Similarity,NSS).NLM去噪算法的核心思想是利用图像的NSS,通过设定的相似窗在搜索窗中搜寻尽可能多且相似的其他像素,将这些像素加权平均得到最终去噪图像,具体计算如下:
其中v为含噪图像,u为去噪图像.
虽然上述算法取得了良好的去噪效果,但通常存在过度平滑等缺陷.此外大多数算法都只在扩散数据的空间域(x空间)进行块组匹配,忽略了数据的扩散向量域(q空间)中包含的信息,这导致在处理复杂结构(如高度弯曲的白质)时,可能会引入新的平滑伪影.针对上述局限,Chen等人[14]提出了一种基于NLM的x-q空间联合去噪算法.该算法首先采用Koay反演技术[15]将莱斯分布的DWI数据转换为类高斯分布数据,然后在x-q空间中的每个采样点上定义一个球形块组,并从中提取旋转不变特征进行块组匹配,最后采用NLM算法进行去噪.针对x-q空间联合去噪,他们还提出了另外一种算法[16],联合图框架变换和NLM算法对DWI数据进行去噪.然而这类方法在提高去噪性能的同时,也增加了处理时间.
与传统滤波方法相比,NLM去噪算法具有简单、性能好、易于改进等优点,但是也普遍存在以下不足:(1)该类算法通常利用单幅图像的NSS,因此利用到的信息冗余度是有限的.(2)在单幅图像中搜索相似块组的质量会受到SNR、分辨率等因素的影响,在加权平均的过程中可能会导致图像模糊或细节丢失,进而影响去噪性能.(3)算法的处理时间严重依赖于搜索窗尺寸和滑动步长.
2.1.2 基于主成分分析去噪算法
PCA是数据分析中常用的降维方法,其利用正交变换,将由线性相关变量表示的观测数据转换为由少数几个线性无关变量(即主成分)表示的数据,以达到降低数据维度且保留原数据主要信息的目的.典型的dMRI扫描通常会产生一个由多幅DWI图像组成的多维数据集,这些图像是采用不同扩散方向和b值对相同解剖结构重复采集获得的,因此具有高度的局部结构自相似性.从PCA的角度来看,这种相似性允许将局部DWI数据内容分解为归属少数信号的主成分,而噪声则分布在所有成分中.由于噪声的非稀疏性,通过减少这种与信号不相关的成分,即可实现去噪.
PCA去噪算法是目前DTI去噪领域的主流算法,这类算法通常包括三个步骤:首先对噪声数据进行奇异值分解(Singular Value Decomposition,SVD),得到主成分基和相关奇异值;然后对奇异值进行处理,通过阈值化的方法减少噪声的影响,常用的阈值操作有硬阈值和软阈值等;最后将原始主成分基与经过处理的奇异值相结合,重建为去噪后的数据.PCA去噪算法的性能高度依赖于奇异值的处理,大多数算法通过估计信号主成分数量并去除仅有噪声的成分来实现去噪[17,18].然而这些算法缺乏客观的阈值标准来区分携带信号的成分和仅有噪声的成分,阈值的选取存在主观性.Veraart等人[19,20]提出了一种基于随机矩阵理论的PCA去噪算法(Marchenko-Pastur Principal Component Analysis,MPPCA),该算法提供了一种客观的阈值截断方案.MPPCA假设dMRI数据中的噪声水平恒定且与信号不相关,因此仅有噪声成分的协方差矩阵特征值服从Marchenko-Pastur分布,通过将满足该分布的特征值置零,从而实现去噪.尽管Marchenko-Pastur分布在理论上仅适用于高斯噪声,但实验结果表明MPPCA能够有效去除dMRI图像中的非高斯噪声,并保留图像中的精细结构.该算法目前已作为MRtrix3[21]软件包的一部分在dMRI各项研究中广泛使用,Cordero-Grande等人[22]还将其推广到复值dMRI数据.
Marchenko-Pastur定律通常假设数据矩阵是无限大的,并且信号成分的数量远小于矩阵的维数,这就导致MPPCA去噪性能严重依赖数据冗余量.为解决这个问题,研究者提出了不同的解决方案[23].Llordén等人[24]将核主成分分析(Kernel Principal Component Analysis,KPCA)去噪技术应用于dMRI数据,该算法通过高斯核将dMRI信号映射到高维核希尔伯特空间,可以同时利用数据中的线性和非线性冗余,实现比MPPCA更好的去噪效果.Olesen等人[25]提出了一种张量MPPCA算法,与MPPCA将数据维度组合在矩阵中不同的是,该算法使用多维数据固有张量结构的每个维度来表征噪声,并递归地估计信号分量,从而更好地利用多维数据中的冗余.
基于PCA的dMRI去噪算法通常受限于与数据维度相关的信号冗余量,而dMRI数据维度通常取决于成像因素,如空间分辨率、b值数量和扩散方向数量等.一些改进的算法虽然可以解决因冗余不足带来的性能受限问题,但同时也增加了算法的复杂性和计算量.
2.1.3 基于低秩矩阵近似去噪算法
由于DWI数据的局部和非局部相似性,可以通过块匹配技术在图像中寻找相似块组,并将这些相似块组堆叠成一个低秩的矩阵,从而将去噪问题视为一个LRMA问题.LRMA问题可以通过低秩矩阵分解(Low Rank Matrix Factorization,LRMF)和核范数最小化(Nuclear Norm Minimization,NNM)来解决.
LRMF方法的核心是SVD,通过限制奇异值的数量或大小来约束矩阵结构的稀疏性,从而给出图像块组矩阵的低秩近似.目前研究者已提出多种奇异值处理方法,其中最优奇异值收缩(Optimal Singular Value Shrinkage,OSVS)是最常用的一种技术.该技术通过对奇异值进行收缩,将小于阈值的奇异值置为零,而保留大于阈值的奇异值,以达到去除噪声的目的.Ma等人[26]提出了一种联合方差稳定变换(Variance Stabilizing Transformation,VST)[27]和OSVS的幅值dMRI去噪框架(简称为VST-OSVS),该框架首先利用VST技术将莱斯分布的dMRI数据转换为类高斯分布数据,然后采用基于块组的OSVS进行去噪,最后通过莱斯偏置校正和逆VST技术得到去噪图像.高阶奇异值分解(Higher-Order Singular Value Decomposition,HOSVD)是SVD在高维数据中的推广,在对多维数据进行分解时,该方法能够充分利用数据每一维度的稀疏性,从而更好地保留数据的拓扑结构.基于块匹配的HOSVD去噪算法能够很好地去除低SNR图像中的噪声,但是会在图像均匀区域引入条形伪影.此外HOSVD去噪算法只适用于加性高斯噪声,不能直接对DWI图像进行处理.为解决这些问题,Zhang等人[28]提出了一种联合VST的全局HOSVD指导下的基于块匹配HOSVD去噪算法(Global Local Higher-Order Singular Value Decomposition,GL-HOSVD),该算法首先对DWI数据进行全局HOSVD预去噪,然后利用预去噪后的图像指导后续基于块匹配的HOSVD去噪.GL-HOSVD在一定程度上减少了噪声退化对HOSVD基的影响,能够有效提高图像质量,然而该算法并没有从原理上解决伪影问题,在块匹配过程中会不可避免地引入伪影.因此Xu等人[29]提出了一种联合HOSVD稀疏约束和莱斯噪声校正的去噪算法,该算法直接对每个局部DWI图像块进行HOSVD去噪,不借助VST技术,也无需构造相似块组,从根本上解决了伪影问题.
LRMF方法的主要局限性在于必须提供秩作为输入,而过低或过高的秩都可能影响去噪效果.因此有研究者采用NNM解决LRMA问题,NNM作为一种凸优化方法,通过对低秩矩阵的奇异值进行软阈值处理来求得最优解.然而NNM对所有奇异值的收缩程度是相同的,忽略了较大奇异值通常代表重要信号成分这一先验知识,因此会导致图像过于平滑.加权核范数最小化(Weighted Nuclear Norm Minimization,WNNM)通过对不同奇异值分配权值,可以获得更加准确的秩估计.通常情况下,奇异值是按照降序排序,而权重是递增的.因此较大的奇异值代表信号的主要成分,包含的图像信息较多,收缩程度较少;反之较小的奇异值对应于噪声的主要成分,包含的图像信息较少,收缩程度较多.WNNM去噪问题通常包括三个步骤:首先对含噪图像块组矩阵进行SVD;接着对奇异值进行收缩,得到一个低秩近似的无噪图像块组矩阵;最后将所有无噪图像块组矩阵进行聚合,得到最终去噪图像.Yi等人[30]首次将WNNM算法应用于DWI数据去噪,在有效去除噪声的同时,保留了图像中较多的纹理细节.Zhao等人[31]则在沿不同扩散方向获取的DWI数据中搜索非局部相似三维块组,并构造低秩矩阵,接着利用WNNM算法进行去噪处理,有效利用了多扩散方向DWI数据中的冗余信息.尽管基于WNNM的去噪算法能够较好地保留DWI图像中的纹理细节,但是其通常受到块组尺寸和滑动步长的限制.块组尺寸较大时,可能意味着更多的结构相似性和更少的NSS,这样会导致局部图像的复杂性增加、细节减少;而滑动步长较大时,可能导致图像块组边缘模糊.反之减小块组尺寸和滑动步长将增加算法处理时间.
除了上述方法,传统DTI去噪算法还包括基于全变分最小化去噪算法[32,33]、基于贝叶斯去噪算法[34,35]、基于稀疏表示和字典学习去噪算法[36,37]等其他去噪算法[38⇓-40].这些算法主要思想是从噪声图像中寻找规律并进行对应的去噪处理,在DTI去噪领域均展现出了良好的去噪性能.然而基于传统图像处理的去噪算法仍存在以下不足:(1)容易引入伪影,可能导致解剖细节特征的丢失.(2)容易受到图像SNR的影响,难以提取全部可用的特征信息,且可能对空间变化的噪声没有鲁棒性.(3)需要复杂的参数设置,计算量大,处理时间较长.(4)通常需要对信号进行某种假设,如Marchenko-Pastur定律假设信号服从高斯分布,LRMA算法假设信号矩阵是低秩的,这些假设在实际情况中可能无法满足,从而限制了这些方法的应用.
2.2 深度学习去噪算法
近年来,以神经网络为基础的深度学习技术已在基于医学成像的疾病诊断、监测和预后等方面展现出了强大的功能,包括图像重建、超分辨率和分割等[41].相较传统的非学习去噪算法,神经网络具有更强的特征提取能力和非线性拟合能力,能够自动学习如何充分利用数据中的冗余,并有效地从噪声图像中还原无噪图像.此外,神经网络还可以通过大量的数据和参数调整来提高去噪性能.
基于深度学习的去噪模型已经被证明在单幅MRI图像去噪方面具有出色的效果[42],然而由于dMRI数据通常包含具有不同图像对比度的图像,且这些图像具有不同的噪声特征,因此这些模型并不能直接用于dMRI去噪.为克服传统去噪算法计算量大、参数选择复杂及难以提取全部有用的特征信息等缺陷,有研究者利用深度学习技术来探索dMRI数据中的冗余,提出了许多新颖的去噪算法[43],这些算法大致可以分为监督学习、无监督学习和自监督学习三类.根据模型的输出结果,这些去噪算法存在两种策略,一种是直接学习从噪声图像到无噪图像的映射;另一种则是先学习从噪声图像到噪声残差图像的映射,然后通过全局残差得到无噪图像.前者能够得到更加稳定的去噪表现,而后者能够更好地保留图像中的结构细节.
2.2.1 基于监督学习的去噪算法
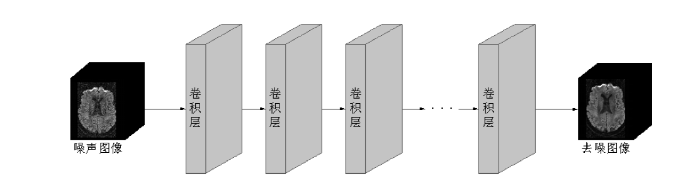
监督学习是深度学习中最常见的方法,这类方法需要有含噪的输入数据和对应无噪的目标数据作为训练样本.通过训练深度神经网络,使其能够从含噪DTI数据中学习噪声的特点,从而输出无噪图像或残差图像.近几年,研究者尝试利用不同神经网络去除DTI数据中的噪声,其中卷积神经网络(Convolutional Neural Networks,CNN)是最常用的网络框架之一.CNN可以自动从大量数据中学习不同的特征表达,能更好地适应不同噪声类型和图像结构,图2展示了三维DTI数据去噪的CNN模型.为加速训练过程,提高网络的去噪性能,通常还需要使用修正线性激活函数(Rectified Linear Unit,ReLU)和批量归一化(Batch Normalization,BN)等技术.Cheng等人[44]使用一维CNN对时域DWI数据进行去噪,由于SOS重建数据会产生比SENSE重建数据更高的噪声,因此该模型采用SENSE重建数据作为目标数据.Jurek等人[45]基于超分辨率CNN(简称为SRCNN)[46]对复值DWI数据进行去噪,在一定程度上减少了莱斯偏置的影响.由于无法获取无噪目标图像,该模型采用迁移学习方法,并利用BrainWeb[47]模拟迁移学习的训练数据.
图2
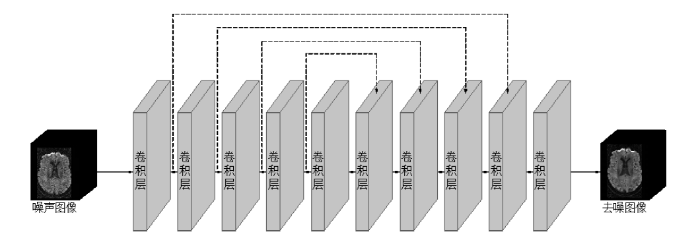
U-Net是一种基于CNN的全卷积网络框架,主要用于图像分割和图像去噪.该框架具有独特的U字形网络结构,由编码器和解码器组成,并通过跳跃连接的方式实现特征融合,图3展示了三维DTI数据去噪的U-Net模型.与经典CNN相比,U-Net在有效去除噪声的同时,能够很好地保留图像的细节信息.Muckley等人[48]提出了一种基于U-Net的模型,旨在去除复值DWI数据中的吉布斯伪影和噪声.为抑制模型的过拟合,该模型采用ImageNet[49]数据库中合成的非MRI图像,来模拟MRI采集以训练网络.受U-Net网络结构的启发,部分模型采用了跳跃连接的结构设计.如Wang等人[50]提出了一种多b值DWI数据联合去噪CNN模型(简称为JD-CNN),该模型能够同时在多个通道进行去噪.类似于U-Net结构,JD-CNN采用共享连接路径隐式地从多b值DWI数据中提取高级共享特征,从而充分利用图像之间的结构相关性.
图3
在DTI计算中,由于扩散张量模型对噪声的高敏感性,实际中需要采集较多的DWI图像来重建高质量的DTI参数图像,这无疑增加了扫描时间和成本.尽管目前已经开发出多种技术来加速重建DTI图像,如压缩感知[51]等,但在实际应用中这些技术需要耗费较多的计算资源.一些研究者从加速DTI重建的角度出发,尝试用尽可能少的DWI图像重建高质量的DTI图像及参数图像[52],这类方法也采用了监督学习的方式.Zhang等人[53]设计了一种去噪CNN模型(简称为DnCNN),并利用残差学习和BN来加速训练过程和提高去噪性能.DnCNN能够有效去除未知噪声水平的高斯噪声,具有较强的通用性,该模型目前已经广泛用于DTI的重建和去噪研究中[54⇓-56].此外Tian等人[57]提出了一种基于残差学习的快速DTI重建模型(简称为DeepDTI),他们首先使用特定的6个扩散编码方向,来获取DWI数据并作为模型的输入,然后计算输入图像和输出真值图像之间的残差来训练模型.结果表明该模型能够获得高质量DWI数据,然而只能通过传统的张量拟合方法,来生成高质量DTI及其参数图.与DeepDTI不同,SuperDTI[58]通过学习DWI图像和对应DTI参数图之间的非线性映射,直接预测高质量DTI参数图,从而避免了传统的张量拟合方法.但是该模型只能预测单个类型的DTI参数图,忽略了参数图与扩散张量场之间的关系.为解决这个问题,Karimi等人[59]提出了一种基于注意力模型的网络,能够从低SNR的DWI图像中获得高质量扩散张量场,并计算得到高质量DTI参数图.然而,该网络并没有利用得到的扩散张量场获取高质量DWI数据.
2.2.2 基于无监督学习的去噪算法
尽管大多数监督学习去噪算法表现优异,但往往需要使用高SNR数据训练模型,而无噪真值图像实际上难以获取,因此降低了这些方法在临床应用中的可行性.一些研究者采用无监督学习来训练神经网络模型,尝试解决这一问题.这类模型不需要人工标记的标签信息,而是从无标记数据中学习数据的结构和特征.Lin等人[60]对深度图像先验(Deep Image Prior,DIP)模型[61]进行了修改,旨在实现对多b值DWI数据的同时去噪.他们使用同一患者采集的高质量先验图像作为网络输入,将所有噪声图像作为网络输出,并通过计算预测图像的SNR来选择最佳去噪结果.然而DIP的去噪性能取决于CNN的迭代次数,由于每幅DWI图像的先验不同,因此必须针对不同DWI图像设置不同最佳参数,才能有效去噪.
除DIP模型外,一些基于CNN的主流无监督学习去噪模型已在自然图像领域展示出了良好的性能,如Noise2Noise[62]、Noise2Self[63]等.Noise2Noise首次提出了噪声的统计独立性思想,通过对独立的噪声图像对进行训练,可以学习到噪声的统计特性和图像的结构信息,从而实现去噪.Noise2Self通过提出J不变性理论,将噪声统计独立性引入自监督学习去噪框架,为自监督学习去噪奠定了理论基础.其他相似的方法,如Noise2Void[64]、Self2Self[65]、Neighbor2Neighbor[66]等也相继被提出,这些方法大多使用具有不同噪声观测值的图像对来训练模型.近年来,有研究者将上述方法的思想应用到DWI去噪中,如Jurek等人[67]提出了一种用于复值dMRI数据的去噪模型,他们首先训练一个相移器来校正相位,然后使用相位校正后的零均值噪声图像训练一个N2N无监督去噪网络.该模型展现出了比幅度图像平均法更好的去噪结果,但是去噪后的图像仍存在部分背景噪声.将N2N无监督去噪网络用于DTI去噪仍是未来的研究重点之一.Fadnavis等人[68]利用J不变性理论提出了一种新的DWI去噪算法(简称为Patch2Self),该算法根据扩散方向将原始四维DWI数据分成多个三维DWI数据,并假设每个三维DWI数据中给定体素的信号,可以与其他三维DWI数据中该体素的p邻域体素信号进行线性回归.由于每个三维DWI数据中的噪声是随机且独立的,因此回归信号可以代表无噪信号,从而实现去噪.Patch2Self充分利用了DWI图像的自相似性,特别适用于较少扩散方向的DWI数据,该算法目前已作为DIPY[69]开源库的一部分在dMRI各项研究中广泛使用.需要注意的是,Patch2Self虽然采用J不变性理论,但并没有利用深度学习中的网络框架,因此严格来讲,该算法并不属于深度学习范畴.
2.2.3 基于自监督学习的去噪算法
上述无监督学习去噪算法能够在单幅DWI图像上取得良好的去噪结果,但未考虑多扩散方向之间的关系.针对这个不足,一些研究者利用自监督学习对DTI图像进行去噪.自监督学习可以视为无监督学习的一种特例,它利用无监督数据自身的结构和特性来进行监督学习和训练,而不依赖人工标记的标签信息.因此自监督学习更加注重数据的内在关系,可以提高模型的鲁棒性和泛化能力.
基于自监督学习的DTI去噪算法从未标记数据中学习潜在的特征表示,并使用这些特征表示来去除噪声.在上文介绍的DeepDTI模型基础上,Tian等人[70]又提出了一种新的DTI自监督去噪模型(简称为SDnDTI).与其他方法不同,该模型不需要额外的高SNR数据作为训练目标.具体来说,SDnDTI的工作原理是首先使用三维CNN对噪声数据的每幅图像进行去噪,并将所有噪声图像的均值作为训练目标,然后对去噪图像进行平均,以获得更高SNR的去噪图像,这一过程称为“先去噪后平均”.Yuan等人[71]提出了一种基于残差学习的心脏DTI自监督去噪模型(简称为SSECNN),该模型包括匹配器和去噪器两个模块.考虑到同b值不同扩散方向获取的DWI图像具有结构相似性,且这些图像中的噪声是独立同分布的,SSECNN采用结构相似度匹配算法从图像中搜索含噪图像对,形成自监督去噪器的训练集.为了克服过度平滑,该模型还引入一种新的边缘加权损失算法,迭代自适应地调整损失权重,从而更好地保留图像的结构细节.
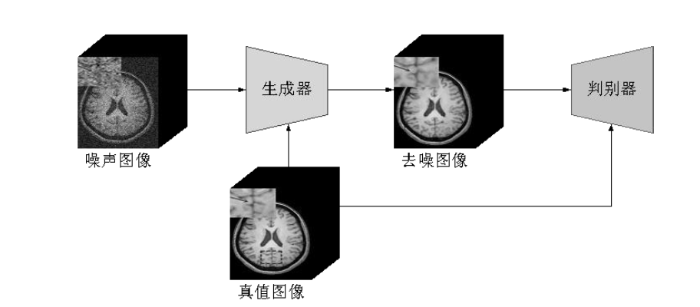
然而自监督学习通常需要大量未标记的噪声数据进行训练,这对于规模有限的数据而言可能是一个挑战.生成模型是机器学习中一类重要的模型,它可以学习数据的分布,生成新的数据样本,因此更适合于小规模数据集.近几年,基于深度学习的生成模型在去噪领域得到了广泛应用,其中最受欢迎的是生成式对抗网络(Generative Adversarial Networks,GAN)和去噪扩散概率模型(简称扩散模型).GAN由生成器和判别器组成,生成器根据输入的噪声图像生成去噪图像,而判别器则根据输入的真值图像来判断去噪图像的真实性.这个过程类似于一场“博弈”,两者不断提升自己的能力,最终达到均衡状态.GAN的出现为无监督去噪提供了新的思路,并在MRI去噪中得到了广泛应用[72],图4展示了该模型.Ran等人[73]提出了一种基于残差编码器-解码器的Wasserstein生成式对抗网络,用于去除三维MRI数据中的噪声并保留图像的解剖细节.Tian等人[74]基于条件生成式对抗网络提出了一种新的MRI去噪模型,该模型采用自编码器结构作为生成器,而判别器使用了马尔可夫判别器.目前GAN在DTI领域的应用仅限于数据生成[75]、重建[76]、超分辨率[77]和失真校正[78]等方面,在去噪方面的研究仍处于起步阶段,还有待深入和扩展.然而,GAN在MRI去噪中表现出的优良性能或许能够为此提供新的思路,该领域仍需要进一步深入研究,并可能成为未来的研究热点.
图4
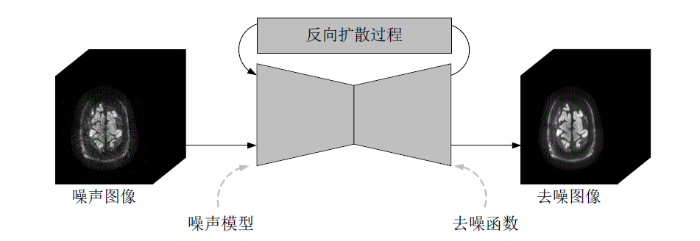
扩散模型[79]是一类强大的概率生成模型,它采用参数化的马尔可夫链,通过变分推理训练,在有限时间内产生与数据匹配的样本.该模型由前向扩散过程和反向扩散过程组成,前向扩散过程向输入数据中添加噪声,并逐渐提高噪声水平,直到数据转化为纯高斯噪声;反向扩散过程旨在从转化后的噪声分布中恢复原始的数据结构,以有效去除前向扩散过程引起的退化.扩散模型目前已广泛用于医学图像的各个领域,包括超分辨率、分割和去噪等[80].Xiang等人[81]提出了一种新的dMRI去噪算法(简称为DDM2),该算法将基于自监督统计的去噪策略引入到扩散模型中,并通过条件生成过程对dMRI数据进行去噪.如图5所示,DDM2包括三个阶段:首先通过自监督方式训练一个去噪函数来学习原始噪声分布;接着从学习到的噪声分布中拟合高斯噪声模型,使噪声输入与扩散马尔可夫链的中间状态相匹配;最后训练一个扩散模型,以无监督方式生成干净图像.与Patch2Self逐体素处理方式不同,DDM2采用逐切片处理方式,不需要大量的输入数据,因此更适合较少扩散方向和规模有限的dMRI数据.相比于GAN,扩散模型具有更加稳定的训练过程,但同时也需要更长的训练时间.作为一种新兴的生成模型,基于扩散模型的dMRI去噪研究仍在不断地发展和探索中.
图5
与传统的非学习去噪算法相比,基于深度学习的DTI去噪技术发展较晚,但表现出了相当甚至更好的去噪性能,且具有更高的计算效率.然而仍然存在许多挑战:(1)首先是数据集问题.大多数模型需要大量的训练数据以避免模型的过拟合,但由于解剖区域、序列参数和硬件配置等的不同,实际上很难获得高质量且多样化的DTI训练集.另外大多数模型的训练或优化需要额外的高SNR数据作为训练目标,这些高质量数据通常是从较长时间的重复扫描中采集到的,而获取这些数据可能具有挑战性.(2)其次是模型的鲁棒性问题.将预先训练好的模型直接应用于使用不同硬件配置和采集参数获取的新数据时,由于这些数据具有不同的图像对比度、空间分辨率和SNR等,模型的去噪性能可能会受到影响.(3)最后是去噪效率问题.增加网络的宽度和深度是提高去噪性能最常用的方式,但同时也会导致更高的算力和更大的内存消耗.因此在保证去噪性能的同时,如何有效地提高去噪速度仍是未来的研究重点.
3 评估标准与常用公开数据集
3.1 评估标准
在去噪过程中,大部分算法会由于噪声滤除不彻底或过度去噪而导致图像信息丢失.因此必须对去噪图像的质量进行判断,以评估算法的去噪性能.评估标准可从主观和客观两个角度来阐述,前者根据观测者的视觉感受来评估图像质量,而后者是根据定量的指标来测量图像质量.虽然主观评估能够较好地反映图像的直观视觉质量,但是该方法容易受到观测者经验及测试环境等因素的影响.为弥补主观评估的不足,需要更加定量的指标对噪声方差的减少和图像精度的提高做出客观评价.目前常用的指标包括:
(1)均方根误差(Root Mean Square Error,RMSE):评估去噪图像和真值图像之间的偏差,该值越小说明去噪图像的质量越高,其计算公式为:
其中m、n表示图像的长和宽,X、Y分别为真值图像和去噪图像,MSE为去噪图像和真值图像的均方误差(Mean Square Error,MSE).
(2)峰值信噪比(Peak Signal to Noise Ratio,PSNR):常用于度量去噪图像的质量,单位为dB,该值越大说明去噪图像残留的噪声越少,去噪效果越好,其计算公式为:
(3)结构相似度(Structure Similarity Index Measure,SSIM):计算去噪图像与原始图像的结构细节相似程度,该值通常在0与1之间,越接近1说明相似程度越高,其计算公式为:
其中
3.2 公开数据集
常用于DTI图像去噪的公开数据集包括:从图像中提取信息数据集(Information Extraction from Images,IXI)、人类脑连接组计划(Human Connectome Project,HCP)、开放存取影像研究(Open Access Series of Imaging Studies,OASIS)、阿尔茨海默症神经影像学计划(Alzheimer’s Disease Neuroimaging Initiative,ADNI)、结构成像验证和评估标准化多次采集(Multiple Acquisitions for Standardization of Structural Imaging Validation and Evaluation,MASSIVE)和快速磁共振数据集(fast Magnetic Resonance Imaging,fastMRI).其中,IXI、HCP、OASIS、ADNI、MASSIVE数据集的成像区域均为脑,而fastMRI数据集的成像区域虽然也包含脑,但仅前列腺区域的成像数据中包含DWI模态.详细的信息在表1中展现.
表1 常用公开数据集
Table 1
| 数据集 | 成像区域 | 描述 | 网站 |
|---|---|---|---|
| IXI | 脑 | 600张健康受试者的MRI图像,包括T1图像、T2图像、DWI图像等. | https://brain-development.org/ixidataset/ |
| HCP | 脑 | 1200名健康受试者的多模态脑MRI图像,包括DWI图像、DTI图像等. | https://humanconnectome.org/ |
| OASIS | 脑 | 正常衰老和阿尔茨海默症的MRI图像,包括T1加权图像、T2加权图像、DTI图像等. | http://www.oasis-brains.org/ |
| ADNI | 脑 | 用于阿尔茨海默病的早期检测和跟踪的影像数据,包括DTI图像、功能MRI图像、结构MRI图像等. | https://adni.loni.usc.edu/ |
| MASSIVE | 脑 | 8000个三维DWI数据,包括b值为0图像、DWI扫描的噪声图像,及10个三维T1图像、T2加权图像等. | https://www.massive-data.org/ |
| fastMRI | 前列腺 | 312次检查的T2加权图像、DWI图像. | https://fastmri.med.nyu.edu/ |
4 实验与讨论
表2 基于传统图像处理的DTI去噪算法比较
Table 2
| 方法 | 第一作者 | 优点 | 缺点 |
|---|---|---|---|
| NLM | Kafali[11] | 利用多次采集的共享结构,对凸集投影算法在各次采集中聚合的复值输出进行处理;能够有效校正相位误差并保留DWI图像细节. | 去噪性能受到块组尺寸的限制. |
| Liu[13] | 使用张量流形来度量扩散张量的相似度,并直接正则化DTI图像;在不模糊图像边界的同时,保留了张量的几何特征,并提高了FA图和纤维束追踪的精度. | 处理时间较长;无法去除原始DWI数据产生的背景噪声. | |
| Chen[14] | 在x-q空间对DWI数据去噪;在不模糊图像边缘的同时,准确去除了复杂结构(如高度弯曲的白质结构)中的噪声. | 处理时间较长. | |
| Chen[16] | 基于图框架变换,充分利用DWI数据的冗余,保留图像的边缘. | 需要较大的计算机内存. | |
| PCA | Manjón[17] | 利用多扩散方向dMRI数据中的冗余,对局部块组奇异值进行阈值化,避免相似块组的搜索过程,减少了处理时间. | PCA阈值的选取存在主观性. |
| Chen[18] | 在两个独立的通道中,分别沿扩散维度,对具有扩散匹配特性相位校正后的DWI数据的实分量和虚分量进行去噪. | 处理时间较长. | |
| Veraart[19,20] | 基于Marchenko-Pastur定律对空间变化的莱斯噪声进行估计,并提出客观的PCA阈值选取方法;利用多扩散方向dMRI数据的冗余. | 去噪性能严重依赖数据冗余量;存在噪声假设. | |
| Llordén[24] | 在不需要满足Marchenko-Pastur定律假设的同时,充分利用了数据的线性和非线性冗余. | 去噪性能依赖核函数. | |
| Olesen[25] | 修改Marchenko-Pastur分布,拓宽MPPCA的适用性;利用多维数据固有张量结构的每个维度来表征噪声,并递归估计信号成分,更好地利用多维数据中的冗余. | 去噪性能受到块组尺寸的限制;存在噪声假设, 即每个块组中的噪声是独立同分布的. | |
| LRMA | Ma[26] | 联合VST和OSVS,对幅值dMRI数据去噪;在有效去除噪声和提高SNR的同时,提高了DTI图及交叉纤维估计的精度. | 基于VST的噪声估计会高估噪声标准差. |
| Zhang[28] | 通过全局HOSVD预去噪,在一定程度上减少了基于块匹配HOSVD阶段噪声退化对HOSVD基的影响. | 去噪性能依赖VST算法;当图像SNR较低时,会引入伪影. | |
| Xu[29] | 联合基于HOSVD稀疏约束和莱斯噪声校正模型,直接对每个局部图像块进行去噪,无需VST技术,从原理上解决了伪影问题. | 去噪性能依赖参数设置. | |
| Zhao[31] | 有效利用不同扩散方向DWI数据的冗余,尤其适用于较少扩散方向或较低b值的DWI数据. | 去噪性能受到块组尺寸的限制. | |
| 全变分最 小化 | Knoll[33] | 通过对扩散张量元素施加全变分约束,直接在目标定量域中进行压缩感知;在加快采集速度的同时,显著减少了参数图中的噪声. | 仅在有限的数据上进行评估. |
| 贝叶斯 | Krajsek[34] | 基于贝叶斯框架对DTI图像进行重建和正则化;在保证张量正定性的同时,考虑了DTI的黎曼几何性质和莱斯噪声的统计特征. | 处理时间较长. |
| Liu[35] | 采用黎曼相似性度量和高斯混合模型学习块组的先验分布;利用贝叶斯推理自适应去噪的同时,保留了DTI图像的非线性结构. | 块匹配过程耗时,且高度依赖图像的先验知识. | |
| 稀疏字典 | Kong[36] | 利用三维DTI数据相邻切片间的冗余来训练自适应稀疏字典. | 处理时间较长. |
| St-Jean[37] | 采用角度邻近匹配以提高稀疏性;通过字典学习进行局部去噪. | 处理时间较长. |
表3 基于深度学习的DTI去噪模型比较
Table 3
| 方法 | 第一作者 | 模型 | 优点 | 缺点 |
|---|---|---|---|---|
| 监督 | Cheng[44] | 1D CNN | 采用SOS-SENSE数据对训练;采用时域去噪,在有效减少训练数据量的同时,更能保留每个体素时间序列的一致性. | 两种重建方式获得的数据的噪声类型不同,影响去噪性能. |
| Jurek[45] | SRCNN | 采用迁移学习方式训练模型;对复值DWI数据去噪,在一定程度上减少了莱斯偏置的影响. | 容易造成边缘模糊. | |
| Muckley[48] | U-Net | 对复值DWI数据去噪,显著去除了DTI参数图中的伪影;采用ImageNet数据集训练模型,能够抑制模型的过拟合. | 仅对单幅DWI图像去噪,忽略了图像间的相关性. | |
| Wang[50] | U-Net | 使用共享连接路径隐式地从多b值DWI数据中提取特征,充分利用图像间的结构相关性. | 容易造成过度去噪. | |
| Tian[57] | 3D CNN | 充分利用了DWI数据的局部和非局部空间信息及扩散编码方向和图像对比度中的冗余;将MRI图像作为训练集的输入,以防止去噪图像模糊. | 传统张量拟合方法对噪声较为敏感,去噪效果受到限制. | |
| Li[58] | U-Net | 直接预测高质量DTI参数图,避免了传统张量拟合方法. | 仅预测单个类型DTI参数图. | |
| 无监督 | Lin[60] | CNN | 基于DIP模型对多b值DWI图像同时去噪. | 采用的数据集类型较为单一. |
| Jurek[67] | SRCNN | 通过N2N范式训练去噪网络,性能优于幅度图像平均法. | 去噪图像存在部分背景噪声. | |
| Fadnavis[68] | / | 利用多扩散方向DWI数据的冗余,特别适用于较少扩散方向数据;逐体素方式去噪. | 去噪性能依赖噪声假设. | |
| 自监督 | Tian[70] | U-Net | 采用“先去噪后平均”的方法,保证输入图像具有更高的SNR;在有效去除噪声的同时,保留了图像的结构信息. | 去噪性能依赖扩散方向数量. |
| Yuan[71] | CNN | 采用SSIM匹配算法搜索含噪图像对;引入一种新的边缘加权损失函数,更好地保留纹理细节. | SSIM指标易受原始图像中噪声的影响. | |
| Xiang[81] | / | 联合自监督统计去噪理论和扩散模型;逐切片方式去噪. | 处理时间较长. |
4.1 实验设计
对去噪方法进行公平的比较是一项相当繁琐的工作,因为这些方法使用了多样化的数据,且针对不同质量的数据需要分别设置最优的参数值.此外,研究者还采用了不同的评估指标来进行验证.为了进行客观的定量分析,本文使用Fiberfox[82]软件通过ISMRM 2015 Tractography Challenge创建的类脑模型[83]生成模拟脑DWI数据.数据大小为90×108×90,各向同性分辨率为2 mm,含有1个b值为0、30个b值为1 000 s/mm2及30个b值为2 000 s/mm2的图像.通过在每9个b值不为0的DWI图像后插入一个b值为0的图像,从而产生一个包括7个b值为0、30个b值为1 000 s/mm2及30个b值为2 000 s/mm2共67个DWI图像的无噪图像集.为了评估在不同噪声水平下的去噪性能,本文将相互独立且具有相同方差的零均值高斯噪声,分别添加到无噪图像的实部和虚部,并通过(4)式合成给定噪声水平的幅值DWI图像.其中噪声水平的定义是底层高斯噪声的最大标准差与无噪图像(b值为0)的最大信号强度的比值,范围为2%至10%,并以2%为增量.
对于模拟的脑DWI数据,本文选择并比较了目前最先进的四种开源去噪算法,分别是文献[19,20]提出的MPPCA算法、文献[26]提出的VST-OSVS算法、文献[28]提出的GL-HOSVD算法与文献[31]提出的联合多扩散方向DWI数据的WNNM算法(简称为WNNM-DWI).在算法的实现过程中,每种算法所涉及的自由参数,分别设置为对应论文中给出的默认值.对于每个噪声水平,本文通过将四种算法实现的去噪图像与无噪图像进行比较,并计算不同b值下的PSNR值和RMSE值来评估去噪图像的质量.为了进一步了解去噪对扩散张量参数图的影响,本文还提供了FA图的RMSE值(简称为FA-RMSE)与彩色编码FA图的RMSE值(简称为Color-coded FA-RMSE),以计算与将扩散张量模型拟合到无噪图像中获得的FA图、彩色编码FA图(简称为Color-coded FA)之间的偏差.其中张量是根据线性最小二乘法估算的,且在计算时剔除了信号最低的体素.需要注意的是,上述所有定量指标都是在去除背景的解剖区域中计算的.
4.2 结果分析
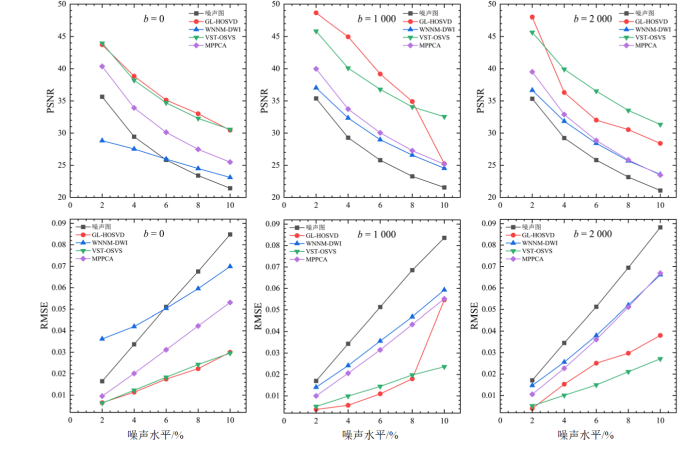
图6展示了在不同噪声水平和b值下,MPPCA、VST-OSVS、GL-HOSVD与WNNM-DWI四种算法在具有莱斯噪声的模拟脑DWI数据上的去噪效果定量比较.由图6的客观评估可以看出,GL-HOSVD算法凭借其利用四维块组中所有维度之间的关系的能力,对低噪声水平和低b值下的DWI图像具有最好的去噪性能;VST-OSVS算法通过联合噪声估计、VST、OSVS和基于块组的策略,可以大大增强高噪声水平和高b值下的DWI图像的质量.与VST-OSVS算法相比,由于噪声退化对HOSVD基的影响,GL-HOSVD算法在高噪声水平和高b值下的去噪效果并不显著.具体而言,对于b值为0的图像,GL-HOSVD算法在PSNR和RMSE两个定量指标方面都优于其他算法.与该算法相比,VST-OSVS算法展现出最接近的结果,而MPPCA算法与WNNM-DWI算法则具有明显的差异.其中,在噪声水平小于6%时,WNNM-DWI算法在所有两个指标方面都差于噪声图像,可能的原因是算法默认的参数值并不适合该模拟DWI数据,导致去噪图像过度平滑.对于b值为1 000 s/mm2的图像,当噪声水平小于8%时,GL-HOSVD算法在所有两个定量指标方面显著优于其他算法;当噪声水平大于8%时,VST-OSVS算法展现出最好的去噪性能,而GL-HOSVD算法则具有与MPPCA算法接近的结果.对于b值为2 000 s/mm2的图像,VST-OSVS算法在所有两个定量指标方面显著优于其他算法,且其PSNR值和RMSE值的改善随着噪声水平的增加而增加,在最高噪声水平10%时观察到了最大的改善.而在2%噪声水平时,GL-HOSVD算法比VST-OSVS算法展现出轻微的优势.
图6
图6
利用模拟DWI数据对四种算法在不同噪声水平和b值下的PSNR和RMSE定量比较.b值单位为s/mm2
Fig. 6
Quantitative comparison of PSNR and RMSE of the four algorithms using the simulated DWI data with different noise levels and b-values. The b-values are in s/mm2
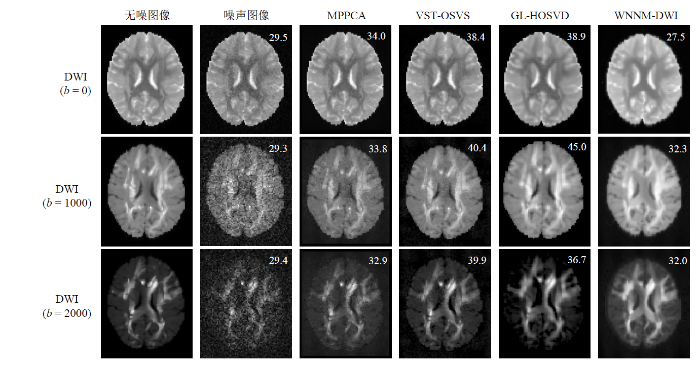
图7展示了在4%噪声水平和不同b值下,MPPCA、VST-OSVS、GL-HOSVD与WNNM-DWI四种算法实现的去噪图像和无噪图像、噪声图像的视觉比较,以及它们对应的PSNR值.对于b值为0和b值为1 000 s/mm2的图像,GL-HOSVD算法取得了最好的去噪效果,在视觉上最接近无噪图像.具体而言,与b值为0噪声图像的PSNR值(29.5 dB)和b值为1 000 s/mm2噪声图像的PSNR值(29.3 dB)相比,GL-HOSVD算法去噪图像的PSNR值分别提高到了38.9 dB和45.0 dB,VST-OSVS算法展现出与GL-HOSVD算法最接近的结果,去噪图像的PSNR值分别为38.4 dB和40.4 dB,而MPPCA算法和WNNM-DWI算法则具有明显的差异.VST-OSVS算法在略微改善b值为0和b值为1 000 s/mm2图像的同时,可以大大改善b值为2 000 s/mm2的图像.而与VST-OSVS算法相比,其他三种算法则具有显著的差异.具体而言,VST-OSVS算法将b值为2 000 s/mm2噪声图像的PSNR值(29.4 dB)提高到了39.9 dB,GL-HOSVD算法、MPPCA算法、WNNM-DWI算法实现的去噪图像的PSNR值分别为36.7 dB、32.9 dB和32.0 dB.
图7
图7
利用模拟DWI数据对四种算法在4%噪声水平和不同b值下的去噪图像和无噪图像、噪声图像的视觉比较.数字是对应的以dB为单位的PSNR,b值单位为s/mm2
Fig. 7
Visual comparison of the denoised images, noise-free images, and noise images of the four algorithms using the simulated DWI data with 4% noise level and different b-values. The numbers reported are PSNR values in dB, and the b-values are in s/mm2
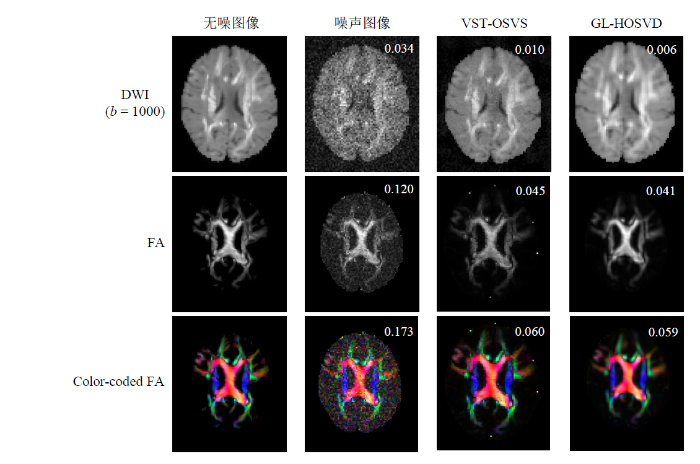
为了更好地对比GL-HOSVD和VST-OSVS两种算法,图8展示了在4%噪声水平和b值为1 000 s/mm2下,两种算法的去噪图像、拟合的FA图、彩色编码FA图与无噪图像、噪声图像的视觉比较,以及它们对应的RMSE值.由图8的客观评估可以看出,两种算法都能显著去除图像中的噪声,但GL-HOSVD算法比VST-OSVS算法更好地保留了图像的细节,在视觉上更接近无噪图像,这与图7中的定量PSNR分析结论一致.与VST-OSVS算法相比,由GL-HOSVD算法去噪图像获得的FA图和彩色编码FA图更接近无噪图像,且对应的FA-RMSE值和Color-coded FA-RMSE值也证明了这一点.这表明GL-HOSVD算法不仅能有效去除图像中的噪声,还很好地保留了扩散张量的各向异性.
图8
图8
利用模拟DWI数据对GL-HOSVD与VST-OSVS算法在4%噪声水平和b值为1 000 s/mm2下的去噪图像、拟合的FA图、彩色编码FA图与无噪图像、噪声图像的视觉比较.数字为对应的RMSE,b值单位为s/mm2
Fig. 8
Visual comparison of the denoised images, fitted FA maps, color-coded FA maps, noise-free images, and noise images of the GL-HOSVD and VST-OSVS algorithms using the simulated DWI data with 4% noise level and b-value of 1 000 s/mm2. The numbers reported are RMSE values, and the b-values are in s/mm2
5 总结与展望
本文首先介绍了DTI的成像原理及噪声分析.接着针对扩散张量图像去噪问题,调研了近年来被广泛研究与使用的去噪算法,并从传统图像处理及深度学习两个方面,着重讨论了扩散张量图像去噪的研究进展.然后提供了去噪评估标准及常用的公开数据集.最后针对文中提及的部分去噪方法进行了实验讨论与分析.
高质量、高SNR的扩散张量图像对大脑微结构成像和中枢神经系统疾病诊断与治疗具有十分重要的意义,因此扩散张量图像去噪问题一直是DTI研究中的重要领域.考虑到现有DTI去噪算法研究的不足,未来该领域的研究应重点关注以下几个方面:
(1)传统DTI去噪算法大都采用线性模型进行建模,然而由于扩散张量图像中的噪声往往具有复杂的空间结构和相关性,这类算法难以有效地去除噪声,且容易产生伪影.一些算法首先利用噪声转换技术(如Koay反演、VST等)预处理DTI数据,然后采用针对高斯噪声设计的去噪方法进行处理,但这类方法高度依赖噪声转换技术.因此在充分保留扩散张量图像细节信息的同时,需要针对不同类型噪声特征选择合适的噪声模型,才能更好地去除噪声.
(2)深度学习DTI去噪模型可以利用大量的训练数据自主选择特征,并借助其自身非线性特性广泛应用于去噪问题.虽然这类算法可以提高不同噪声类型数据的质量,且具有高度自适应性和泛化性能,但它需要大量的训练数据和复杂的网络结构.因此在选择合适的网络框架的同时,可以结合传统图像处理算法来提高DTI去噪性能和效率.
(3)大部分去噪算法专注于DTI数据的幅度域,忽略了固有的空间域信息.有研究表明,在幅度域简单地提高图像SNR并不能有效去除噪声基底,对复数域数据进行去噪可能更加有效.此外大多数DTI去噪算法都只在矩阵层次上处理数据,这种方式在数据矩阵化的过程中可能会破坏扩散张量图像的拓扑结构.张量作为矩阵的高阶推广,可以更好地保留图像结构,且能够充分利用高维数据不同维度间的相关性.因此,针对高阶张量下的DTI去噪算法的研究是一个有挑战性但具有潜力的方向.
利益冲突
无
参考文献
DTI brain template construction based on gaussian averaging
[J].
基于高斯平均的DTI脑模板构建方法
[J].
DOI:10.11938/cjmr20212957
[本文引用: 1]

在获取被试的张量数据后通常对其进行多通道线性平均以得到张量模板.但线性平均不仅会忽略张量中的向量信息,还会使灰质和白质的交界处过于平滑,降低模板的分辨率.为了解决以上问题,本文引入了四元数及高斯加权平均来构建高斯扩散张量成像(Diffusion Tensor Imaging,DTI)脑模板.本文首先对55个健康被试的DTI数据进行预处理,使得数据伪影最小化;再通过扩散张量成像工具包(Diffusion Tensor Imaging ToolKit,DTI-TK)将预处理后的数据进行初步空间标准化;然后将张量通过特征分解得到特征向量和特征值;最后,将由特征向量转化的四元数标量和特征值分别进行高斯加权平均得到平均后的特征向量和特征值,并对其进行重建得到张量模板.实验结果表明相比于线性DTI模板,高斯DTI模板在DTED、COH、DVED、OVL、corr<sub>FA</sub>评估指标上表现更优,而IA指标较差,说明本文提出的高斯DTI模板在整体信息保留方面有所优化,但方向信息有所丢失.
An intrinsic anisotropic feature of DTI images derived by geometric properties on the riemannian manifold
[J].
A fiber tracking algorithm based on non-local constrained spherical deconvolution
[J].
基于非局部约束球面反卷积模型的纤维追踪算法
[J].
DOI:10.11938/cjmr20192798
[本文引用: 1]

基于扩散磁共振成像的纤维追踪技术为非侵入性观测脑白质结构提供了有力的手段,约束球面反卷积作为一种多纤维追踪模型,能够对体素内纤维的方向信息进行建模,进而实现脑纤维的重构.针对约束球面反卷积模型的不适定性以及细节信息丢失问题,本文在约束球面反卷积的基础上,结合邻域信息和分数阶正则化,提出了一种基于非局部约束球面反卷积模型的确定型纤维追踪算法,分数阶的非局部特性使得纤维方向分布模型估计的误差更小,而邻域信息的引入保证了空间一致性,可以减少噪声的影响.分别利用模拟数据、人脑实际数据对本文算法及基于约束球面反卷积的确定型纤维追踪算法作对比实验,结果表明,利用本文算法追踪的纤维不仅整体视觉效果上较整洁,而且对交叉纤维的重建结果更完整准确.
New challenges and future perspectives in brain imaging methods
[J].
Brain fiber structure estimation based on principal component analysis and RINLM filter
[J].
A survey on state-of-the-art denoising techniques for brain magnetic resonance images
[J].
What’s new and what’s next in diffusion MRI preprocessing
[J].
MRI denoising using non-local means
[J].
DOI:10.1016/j.media.2008.02.004
PMID:18381247
[本文引用: 1]

Magnetic Resonance (MR) images are affected by random noise which limits the accuracy of any quantitative measurements from the data. In the present work, a recently proposed filter for random noise removal is analyzed and adapted to reduce this noise in MR magnitude images. This parametric filter, named Non-Local Means (NLM), is highly dependent on the setting of its parameters. The aim of this paper is to find the optimal parameter selection for MR magnitude image denoising. For this purpose, experiments have been conducted to find the optimum parameters for different noise levels. Besides, the filter has been adapted to fit with specific characteristics of the noise in MR image magnitude images (i.e. Rician noise). From the results over synthetic and real images we can conclude that this filter can be successfully used for automatic MR denoising.
New methods for MRI denoising based on sparseness and self-similarity
[J].
DOI:10.1016/j.media.2011.04.003
PMID:21570894
[本文引用: 1]

This paper proposes two new methods for the three-dimensional denoising of magnetic resonance images that exploit the sparseness and self-similarity properties of the images. The proposed methods are based on a three-dimensional moving-window discrete cosine transform hard thresholding and a three-dimensional rotationally invariant version of the well-known nonlocal means filter. The proposed approaches were compared with related state-of-the-art methods and produced very competitive results. Both methods run in less than a minute, making them usable in most clinical and research settings.Copyright © 2011 Elsevier B.V. All rights reserved.
Phase-correcting non-local means filtering for diffusion-weighted imaging of the spinal cord
[J].DOI:10.1002/mrm.27105 PMID:29427379 [本文引用: 2]
Non-local mean denoising in diffusion tensor space
[J].The aim of the present study was to present a novel non-local mean (NLM) method to denoise diffusion tensor imaging (DTI) data in the tensor space. Compared with the original NLM method, which uses intensity similarity to weigh the voxel, the proposed method weighs the voxel using tensor similarity measures in the diffusion tensor space. Euclidean distance with rotational invariance, and Riemannian distance and Log-Euclidean distance with affine invariance were implemented to compare the geometric and orientation features of the diffusion tensor comprehensively. The accuracy and efficacy of the proposed novel NLM method using these three similarity measures in DTI space, along with unbiased novel NLM in diffusion-weighted image space, were compared quantitatively and qualitatively in the present study.
Diffusion tensor image denoising via geometric invariant nonlocal means on the tensor manifold
[J].
Noise reduction in diffusion MRI using non-local self-similar information in joint x-q space
[J].
DOI:S1361-8415(18)30391-8
PMID:30703580
[本文引用: 2]

Diffusion MRI affords valuable insights into white matter microstructures, but suffers from low signal-to-noise ratio (SNR), especially at high diffusion weighting (i.e., b-value). To avoid time-intensive repeated acquisition, post-processing algorithms are often used to reduce noise. Among existing methods, non-local means (NLM) has been shown to be particularly effective. However, most NLM algorithms for diffusion MRI focus on patch matching in the spatial domain (i.e., x-space) and disregard the fact that the data live in a combined 6D space covering both spatial domain and diffusion wavevector domain (i.e., q-space). This drawback leads to inaccurate patch matching in curved white matter structures and hence the inability to effectively use recurrent information for noise reduction. The goal of this paper is to overcome this limitation by extending NLM to the joint x-q space. Specifically, we define for each point in the x-q space a spherical patch from which we extract rotation-invariant features for patch matching. The ability to perform patch matching across q-samples allows patches from differentially orientated structures to be used for effective noise removal. Extensive experiments on synthetic, repeated-acquisition, and HCP data demonstrate that our method outperforms state-of-the-art methods, both qualitatively and quantitatively.Copyright © 2019 Elsevier B.V. All rights reserved.
A signal tra nsformational framework for breaking the noise floor and its applications in MRI
[J].
Denoising of diffusion MRI data via graph framelet matching in xq space
[J].
Diffusion weighted image denoising using overcomplete local PCA
[J].
A diffusion-matched principal component analysis (DM-PCA) based two-channel denoising procedure for high-resolution diffusion-weighted MRI
[J].
Diffusion MRI noise mapping using random matrix theory
[J].
DOI:10.1002/mrm.26059
PMID:26599599
[本文引用: 3]

To estimate the spatially varying noise map using a redundant series of magnitude MR images.We exploit redundancy in non-Gaussian distributed multidirectional diffusion MRI data by identifying its noise-only principal components, based on the theory of noisy covariance matrices. The bulk of principal component analysis eigenvalues, arising due to noise, is described by the universal Marchenko-Pastur distribution, parameterized by the noise level. This allows us to estimate noise level in a local neighborhood based on the singular value decomposition of a matrix combining neighborhood voxels and diffusion directions.We present a model-independent local noise mapping method capable of estimating the noise level down to about 1% error. In contrast to current state-of-the-art techniques, the resultant noise maps do not show artifactual anatomical features that often reflect physiological noise, the presence of sharp edges, or a lack of adequate a priori knowledge of the expected form of MR signal.Simulations and experiments show that typical diffusion MRI data exhibit sufficient redundancy that enables accurate, precise, and robust estimation of the local noise level by interpreting the principal component analysis eigenspectrum in terms of the Marchenko-Pastur distribution. Magn Reson Med 76:1582-1593, 2016. © 2015 International Society for Magnetic Resonance in Medicine.© 2015 International Society for Magnetic Resonance in Medicine.
Denoising of diffusion MRI using random matrix theory
[J].
DOI:S1053-8119(16)30394-9
PMID:27523449
[本文引用: 3]

We introduce and evaluate a post-processing technique for fast denoising of diffusion-weighted MR images. By exploiting the intrinsic redundancy in diffusion MRI using universal properties of the eigenspectrum of random covariance matrices, we remove noise-only principal components, thereby enabling signal-to-noise ratio enhancements. This yields parameter maps of improved quality for visual, quantitative, and statistical interpretation. By studying statistics of residuals, we demonstrate that the technique suppresses local signal fluctuations that solely originate from thermal noise rather than from other sources such as anatomical detail. Furthermore, we achieve improved precision in the estimation of diffusion parameters and fiber orientations in the human brain without compromising the accuracy and spatial resolution.Copyright © 2016 Elsevier Inc. All rights reserved.
MRtrix3: a fast, flexible and open software framework for medical image processing and visualisation
[J].
Complex diffusion-weighted image estimation via matrix recovery under general noise models
[J].
Noise reduction with distribution corrected (NORDIC) PCA in dMRI with complex-valued parameter-free locally low-rank processing
[J].
SNR-enhanced diffusion MRI with structure-preserving low-rank denoising in reproducing kernel hilbert spaces
[J].
Tensor denoising of multidimensional MRI data
[J].
Denoise magnitude diffusion magnetic resonance images via variance-stabilizing transformation and optimal singular-value manipulation
[J].
Noise estimation and removal in MR imaging: the variance-stabilization approach
[C]//
Denoise diffusion-weighted images using higher-order singular value decomposition
[J].
DOI:S1053-8119(17)30309-9
PMID:28416450
[本文引用: 3]

Noise usually affects the reliability of quantitative analysis in diffusion-weighted (DW) magnetic resonance imaging (MRI), especially at high b-values and/or high spatial resolution. Higher-order singular value decomposition (HOSVD) has recently emerged as a simple, effective, and adaptive transform to exploit sparseness within multidimensional data. In particular, the patch-based HOSVD denoising has demonstrated superb performance when applied to T1-, T2-, and proton density-weighted MRI data. In this study, we aim to investigate the feasibility of denoising DW data using the HOSVD transform. With the low signal-to-noise ratio in typical DW data, the patch-based HOSVD denoising suffers from stripe artifacts in homogeneous regions because of the HOSVD bases learned from the noisy patches. To address this problem, we propose a novel denoising method. It first introduces a global HOSVD-based denoising as a prefiltering stage to guide the subsequent patch-based HOSVD denoising stage. The HOSVD bases from the patch groups in prefiltered images are then used to transform the noisy patch groups in original DW data. Experiments were performed using simulated and in vivo DW data. Results show that the proposed method significantly reduces stripe artifacts compared with conventional patch-based HOSVD denoising methods, and outperforms two state-of-the-art denoising methods in terms of denoising quality and diffusion parameters estimation.Copyright © 2017. Published by Elsevier Inc.
A diffusion-weighted image denoising algorithm using HOSVD combined with rician noise corrected model
[J].
基于高阶奇异值分解和Rician噪声校正模型的扩散加权图像去噪算法
[J].
DOI:10.12122/j.issn.1673-4254.2021.09.16
[本文引用: 2]

目的 研究一种新颖的基于高阶奇异值分解(HOSVD)的扩散加权图像去噪算法,用以提高扩散加权(DW)图像的信噪比以及后续量化参数的准确性。方法 我们提出一种基于HOSVD稀疏约束和Rician噪声校正模型的去噪方法,将Rician噪声信号期望融合到传统的HOSVD去噪框架中,从而能够直接对带有Rician噪声的DW图像进行去噪。此外,考虑到对相似块组成的高维数组进行HOSVD去噪处理,容易引入条形伪影,因此本文直接对每个局部DW图像块进行HOSVD去噪,从而解决了条形伪影问题。为了验证所提方法的有效性,我们将本方法与低秩+边缘约束(LR+Edge)、基于全局指导下的局部高阶奇异值分解(GL-HOSVD)、基于块匹配的三维滤波(BM3D)和非局部均值(NLM)4种去噪算法进行了实验对比。结果 实验结果表明,所提方法能够有效降低DW图像噪声,同时较好的保留图像细节以及边缘结构信息。无论是从DW图像的峰值信噪比(PSNR)和结构相似性(SSIM)以及各向异性分数均方根误差定量指标,还是从去噪图像和各向异性分数图的视觉效果来看,本算法都要明显优于LR+Edge,BM3D和NLM。此外,GL-HOSVD虽然可以得到较好的去噪结果,但是在高噪声水平下,会引入条形伪影,而本文方法不但可以得到较好的去噪结果,并且不存在伪影问题。结论 本文提出了一种新颖的HOSVD去噪方法,可以直接处理带有Rician噪声的DW图像,并且解决了同类算法中伪影问题,去噪效果明显,能够为临床提供更准确的量化参数结果,更好服务于临床影像诊断。
Application of weighted nuclear norm denoising algorithm in diffusion-weighted image
[J].
加权核范数降噪算法在扩散加权图像中的应用
[J].
Joint denoising of diffusion-weighted images via structured low-rank patch matrix approximation
[J].
DOI:10.1002/mrm.29407
PMID:36178232
[本文引用: 3]

To develop a joint denoising method that effectively exploits natural information redundancy in MR DWIs via low-rank patch matrix approximation.A denoising method is introduced to jointly reduce noise in DWI dataset by exploiting nonlocal self-similarity as well as local anatomical/structural similarity within multiple 2D DWIs acquired with the same anatomical geometry but different diffusion directions. Specifically, for each small 3D reference patch sliding within 2D DWI, nonlocal but similar patches are searched by matching image contents within entire DWI dataset and then structured into a patch matrix. The resulting patch matrices are denoised by enforcing low-rankness via weighted nuclear norm minimization and finally are back-distributed to DWI space. The proposed procedure was evaluated with simulated and in vivo brain diffusion tensor imaging (DTI) datasets and then compared to existing Marchenko-Pastur principal component analysis denoising method.The proposed method achieved significant noise reduction while preserving structural details in all DWIs for both simulated and in vivo datasets. Quantitative evaluation of error maps demonstrated it consistently outperformed Marchenko-Pastur principal component analysis method. Further, the denoised DWIs led to substantially improved DTI parametric maps, exhibiting significantly less noise and revealing more microstructural details.The proposed method denoises DWI dataset by utilizing both nonlocal self-similarity and local structural similarity within DWI dataset. This weighted nuclear norm minimization-based low-rank patch matrix denoising approach is effective and highly applicable to various diffusion MRI applications, including DTI as a postprocessing procedure.© 2022 International Society for Magnetic Resonance in Medicine.
Denoising diffusion MRI via graph total variance in spatioangular domain
[J].
A model-based reconstruction for undersampled radial spin-echo DTI with variational penalties on the diffusion tensor
[J].
DOI:10.1002/nbm.3258
PMID:25594167
[本文引用: 2]

Radial spin-echo diffusion imaging allows motion-robust imaging of tissues with very low T2 values like articular cartilage with high spatial resolution and signal-to-noise ratio (SNR). However, in vivo measurements are challenging, due to the significantly slower data acquisition speed of spin-echo sequences and the less efficient k-space coverage of radial sampling, which raises the demand for accelerated protocols by means of undersampling. This work introduces a new reconstruction approach for undersampled diffusion-tensor imaging (DTI). A model-based reconstruction implicitly exploits redundancies in the diffusion-weighted images by reducing the number of unknowns in the optimization problem and compressed sensing is performed directly in the target quantitative domain by imposing a total variation (TV) constraint on the elements of the diffusion tensor. Experiments were performed for an anisotropic phantom and the knee and brain of healthy volunteers (three and two volunteers, respectively). Evaluation of the new approach was conducted by comparing the results with reconstructions performed with gridding, combined parallel imaging and compressed sensing and a recently proposed model-based approach. The experiments demonstrated improvements in terms of reduction of noise and streaking artifacts in the quantitative parameter maps, as well as a reduction of angular dispersion of the primary eigenvector when using the proposed method, without introducing systematic errors into the maps. This may enable an essential reduction of the acquisition time in radial spin-echo diffusion-tensor imaging without degrading parameter quantification and/or SNR.Copyright © 2015 John Wiley & Sons, Ltd.
A riemannian bayesian framework for estimating diffusion tensor images
[J].
Diffusion tensor imaging denoising based on riemann nonlocal similarity
[J].
Noise reduction of diffusion tensor images by sparse representation and dictionary learning
[J].
Non local spatial and angular matching: enabling higher spatial resolution diffusion MRI datasets through adaptive denoising
[J].
Adaptive phase correction of diffusion-weighted images
[J].
Gaussianization of diffusion MRI data using spatially adaptive filtering
[J].
High-resolution multi-shot diffusion-weighted MRI combining markerless prospective motion correction and locally low-rank constrained reconstruction
[J].
Deep learning on image denoising: an overview
[J].
DOI:S0893-6080(20)30266-5
PMID:32829002
[本文引用: 1]

Deep learning techniques have received much attention in the area of image denoising. However, there are substantial differences in the various types of deep learning methods dealing with image denoising. Specifically, discriminative learning based on deep learning can ably address the issue of Gaussian noise. Optimization models based on deep learning are effective in estimating the real noise. However, there has thus far been little related research to summarize the different deep learning techniques for image denoising. In this paper, we offer a comparative study of deep techniques in image denoising. We first classify the deep convolutional neural networks (CNNs) for additive white noisy images; the deep CNNs for real noisy images; the deep CNNs for blind denoising and the deep CNNs for hybrid noisy images, which represents the combination of noisy, blurred and low-resolution images. Then, we analyze the motivations and principles of the different types of deep learning methods. Next, we compare the state-of-the-art methods on public denoising datasets in terms of quantitative and qualitative analyses. Finally, we point out some potential challenges and directions of future research.Copyright © 2020 Elsevier Ltd. All rights reserved.
CNN-DMRI: a convolutional neural network for denoising of magnetic resonance images
[J].
Deep learning for image enhancement and correction in magnetic resonance imaging—state-of-the-art and challenges
[J].
Denoising diffusion weighted imaging data using convolutional neural networks
[J].
Supervised denoising of diffusion-weighted magnetic resonance images using a convolutional neural network and transfer learning
[J].
Image super-resolution using deep convolutional networks
[J].
MRI simulation-based evaluation of image-processing and classification methods
[J].With the increased interest in computer-aided image analysis methods, there is a greater need for objective methods of algorithm evaluation. Validation of in vivo MRI studies is complicated by a lack of reference data and the difficulty of constructing anatomically realistic physical phantoms. We present here an extensible MRI simulator that efficiently generates realistic three-dimensional (3-D) brain images using a hybrid Bloch equation and tissue template simulation that accounts for image contrast, partial volume, and noise. This allows image analysis methods to be evaluated with controlled degradations of image data.
Training a neural network for gibbs and noise removal in diffusion MRI
[J].
Imagenet: A large-scale hierarchical image database
[C]//
High-field mr diffusion-weighted image denoising using a joint denoising convolutional neural network
[J].
DOI:10.1002/jmri.26761
PMID:31012226
[本文引用: 2]

Low signal-to-noise ratio (SNR) has been a major limiting factor for the application of higher-resolution diffusion-weighted imaging (DWI). Most of the conventional denoising models suffer from the drawbacks of shallow feature extraction and hand-crafted parameter tuning. Although multiple studies have shown the promising applications of image denoising using convolutional neural networks (CNNs), none of them have considered denoising multiple b-value DWIs using a multichannel CNN model.To present a joint denoising CNN (JD-CNN) model to improve the SNR of multiple b-value DWI.Retrospective technical development.Twenty healthy rats and two rats with clinically confirmed focal cortical dysplasia were included to evaluate the performance of the proposed method.11.7T MRI, a multiple b-values DWI sequence.The total variation (TV) and BM3D denoising methods were also performed on the same dataset for comparison. Peak SNR (PSNR) and normalized mean square error (NMSE) were calculated for the assessment of image qualities.A paired Student's t-test was conducted to compare the diffusion parameter measurements between different approaches. P < 0.01 was considered statistically significant.Simulation results showed substantial improvement of image quality after JD-CNN denoising (PSNR of original image: 23.15 ± 1.77; PSNR of denoised image: 42.94 ± 2.12). The proposed method outperforms the state-of-the-art methods on high b-value DWIs in terms of PSNR (TV: 33.51 ± 0.83, BM3D: 35.12 ± 0.94, JD-CNN: 46.52 ± 0.98). In addition, the NMSE of the estimated apparent diffusion coefficient (ADC) reduces from 0.72 ± 0.13 to 0.45 ± 0.06 (P < 0.01) with the application of the JD-CNN model.The proposed method is able to remove noise with a wide range of noise levels in multiple b-value DWI and improve the diffusion parameter estimation. This shows potential clinical promise.2 Technical Efficacy Stage: 2 J. Magn. Reson. Imaging 2019;50:1937-1947.© 2019 International Society for Magnetic Resonance in Medicine.
Acceleration of three-dimensional diffusion magnetic resonance imaging using a kernel low-rank compressed sensing method
[J].
Super-resolved q-space deep learning with uncertainty quantification
[J].
Beyond a gaussian denoiser: residual learning of deep cnn for image denoising
[J].
DOI:10.1109/TIP.2017.2662206
PMID:28166495
[本文引用: 1]

The discriminative model learning for image denoising has been recently attracting considerable attentions due to its favorable denoising performance. In this paper, we take one step forward by investigating the construction of feed-forward denoising convolutional neural networks (DnCNNs) to embrace the progress in very deep architecture, learning algorithm, and regularization method into image denoising. Specifically, residual learning and batch normalization are utilized to speed up the training process as well as boost the denoising performance. Different from the existing discriminative denoising models which usually train a specific model for additive white Gaussian noise at a certain noise level, our DnCNN model is able to handle Gaussian denoising with unknown noise level (i.e., blind Gaussian denoising). With the residual learning strategy, DnCNN implicitly removes the latent clean image in the hidden layers. This property motivates us to train a single DnCNN model to tackle with several general image denoising tasks, such as Gaussian denoising, single image super-resolution, and JPEG image deblocking. Our extensive experiments demonstrate that our DnCNN model can not only exhibit high effectiveness in several general image denoising tasks, but also be efficiently implemented by benefiting from GPU computing.
Accelerating prostate diffusion-weighted MRI using a guided denoising convolutional neural network: retrospective feasibility study
[J].
Accelerated acquisition of high-resolution diffusion-weighted imaging of the brain with a multi-shot echo-planar sequence: deep-learning-based denoising
[J].
Accelerating whole-body diffusion-weighted MRI with deep learning-based denoising image filters
[J].
DeepDTI: high-fidelity six-direction diffusion tensor imaging using deep learning
[J].
SuperDTI: ultrafast DTI and fiber tractography with deep learning
[J].
DOI:10.1002/mrm.28937
PMID:34309073
[本文引用: 2]

To develop a deep learning-based reconstruction framework for ultrafast and robust diffusion tensor imaging and fiber tractography.SuperDTI was developed to learn the nonlinear relationship between DWIs and the corresponding diffusion tensor parameter maps. It bypasses the tensor fitting procedure, which is highly susceptible to noises and motions in DWIs. The network was trained and tested using data sets from the Human Connectome Project and patients with ischemic stroke. Results from SuperDTI were compared against widely used methods for tensor parameter estimation and fiber tracking.Using training and testing data acquired using the same protocol and scanner, SuperDTI was shown to generate fractional anisotropy and mean diffusivity maps, as well as fiber tractography, from as few as six raw DWIs, with a quantification error of less than 5% in all white-matter and gray-matter regions of interest. It was robust to noises and motions in the testing data. Furthermore, the network trained using healthy volunteer data showed no apparent reduction in lesion detectability when directly applied to stroke patient data.Our results demonstrate the feasibility of superfast DTI and fiber tractography using deep learning with as few as six DWIs directly, bypassing tensor fitting. Such a significant reduction in scan time may allow the inclusion of DTI into the clinical routine for many potential applications.© 2021 International Society for Magnetic Resonance in Medicine.
Diffusion tensor estimation with transformer neural networks
[J].
Denoising of multi b-value diffusion-weighted MR images using deep image prior
[J].
Deep image prior
[C]//
Noise2noise: learning image restoration without clean data
[J].
Noise2self: blind denoising by self-supervision
[C]//
Noise2void-learning denoising from single noisy images
[C]//
Self2self with dropout: learning self-supervised denoising from single image
[C]//
Neighbor2neighbor: self-supervised denoising from single noisy images
[C]//
Phase correction and noise-to-noise denoising of diffusion magnetic resonance images using neural networks
[C]//
Patch2self: denoising diffusion MRI with self-supervised learning
[J].
Dipy, a library for the analysis of diffusion MRI data
[J].
DOI:10.3389/fninf.2014.00008
PMID:24600385
[本文引用: 1]

Diffusion Imaging in Python (Dipy) is a free and open source software project for the analysis of data from diffusion magnetic resonance imaging (dMRI) experiments. dMRI is an application of MRI that can be used to measure structural features of brain white matter. Many methods have been developed to use dMRI data to model the local configuration of white matter nerve fiber bundles and infer the trajectory of bundles connecting different parts of the brain. Dipy gathers implementations of many different methods in dMRI, including: diffusion signal pre-processing; reconstruction of diffusion distributions in individual voxels; fiber tractography and fiber track post-processing, analysis and visualization. Dipy aims to provide transparent implementations for all the different steps of dMRI analysis with a uniform programming interface. We have implemented classical signal reconstruction techniques, such as the diffusion tensor model and deterministic fiber tractography. In addition, cutting edge novel reconstruction techniques are implemented, such as constrained spherical deconvolution and diffusion spectrum imaging (DSI with deconvolution, as well as methods for probabilistic tracking and original methods for tractography clustering. Many additional utility functions are provided to calculate various statistics, informative visualizations, as well as file-handling routines to assist in the development and use of novel techniques. In contrast to many other scientific software projects, Dipy is not being developed by a single research group. Rather, it is an open project that encourages contributions from any scientist/developer through GitHub and open discussions on the project mailing list. Consequently, Dipy today has an international team of contributors, spanning seven different academic institutions in five countries and three continents, which is still growing.
SDnDTI: self-supervised deep learning-based denoising for diffusion tensor MRI
[J].
Self-supervised structural similarity-based convolutional neural network for cardiac diffusion tensor image denoising
[J].
DOI:10.1002/mp.16301
PMID:36775901
[本文引用: 2]

Diffusion tensor imaging (DTI) is a promising technique for non-invasively investigating the myocardial fiber structures of human heart. However, low signal-to-noise ratio has been a major limit of cardiac DTI to prevent us from detecting myocardium structure accurately. Therefore, it is important to remove the effect of noise on DW images.Although the conventional and deep learning-based denoising methods have shown the potential to deal with effectively the noise in diffusion weighted (DW) images, most of them are redundant information dependent or require the noise-free images as golden standard. In addition, the existed DW image denoising methods often suffer from problems of over-smoothing. To address these issues, we propose a self-supervised learning model, structural similarity based convolutional neural network with edge-weighted loss (SSECNN), to remove the noise effectively in cardiac DTI.Considering that the DW images acquired along different diffusion directions have structural similarity, and the noise in these DW images is independent and identically distributed, the structural similarity-based matching algorithm is proposed to search for the most similar DW images. Such similar noisy DW image pairs are then used as the input and target of the denoising network SSECNN, which consists of several convolutional and residual blocks. Through the self-supervised training with these image pairs, the network can restore the clean DW images and retain the correlations between the denoised DW images along different directions. To avoid the over-smoothing problem, we design a novel edge-weighted loss which enables the network to adaptively adjust the loss weights with iterations and therefore to improve the detail preserve ability of the model. To verify the superiority of the proposed method, comparisons with state-of-the-art (SOTA) denoising methods are performed on both synthetic and real acquired DTI datasets.Experimental results show that SSECNN can effectively reduce the noise in the DW images while preserving detailed texture and edge information and therefore achieve better performance in DTI reconstruction. For synthetic dataset, compared to the SOTA method, the root mean square error (RMSE), peak signal to noise ratio (PSNR) and structure similarity (SSIM) between the denoised DW images obtained with SSECNN and noise-free DW images are improved by 6.94%, 1.98% and 0.76% respectively when the noise level is 10%. As for the acquired cardiac DTI dataset, the SSECNN method could significantly improve signal to noise ratio (SNR) and contrast to noise ratio (CNR) of cardiac DW images and achieve more regular helix angle (HA) and transverse angle (TA) maps. The ablation experimental results validate that using the structure similarity-based method to search the similar DW image pairs yield the smallest loss, and with the help of the edge-weighted loss, the denoised DW images and diffusion metric maps can preserve more details.The proposed SSECNN method can fully explore the similarity between the DW images along different diffusion directions. Using such similarity and an edge-weighted loss enable us to denoise cardiac DTI effectively in a self-supervised manner. Our method can overcome the redundancy information dependence and over-smoothing problem of the SOTA methods. This article is protected by copyright. All rights reserved.This article is protected by copyright. All rights reserved.
The role of generative adversarial networks in brain MRI: a scoping review
[J].
Denoising of 3D magnetic resonance images using a residual encoder-decoder wasserstein generative adversarial network
[J].
DOI:S1361-8415(18)30653-4
PMID:31085444
[本文引用: 1]

Structure-preserved denoising of 3D magnetic resonance imaging (MRI) images is a critical step in medical image analysis. Over the past few years, many algorithms with impressive performances have been proposed. In this paper, inspired by the idea of deep learning, we introduce an MRI denoising method based on the residual encoder-decoder Wasserstein generative adversarial network (RED-WGAN). Specifically, to explore the structure similarity between neighboring slices, a 3D configuration is utilized as the basic processing unit. Residual autoencoders combined with deconvolution operations are introduced into the generator network. Furthermore, to alleviate the oversmoothing shortcoming of the traditional mean squared error (MSE) loss function, the perceptual similarity, which is implemented by calculating the distances in the feature space extracted by a pretrained VGG-19 network, is incorporated with the MSE and adversarial losses to form the new loss function. Extensive experiments are implemented to assess the performance of the proposed method. The experimental results show that the proposed RED-WGAN achieves performance superior to several state-of-the-art methods in both simulated and real clinical data. In particular, our method demonstrates powerful abilities in both noise suppression and structure preservation.Copyright © 2019 Elsevier B.V. All rights reserved.
Boosting magnetic resonance image denoising with generative adversarial networks
[J].
Synthesis of diffusion-weighted MRI scalar maps from flair volumes using generative adversarial networks
[J].
Multi-channel GAN-based calibration-free diffusion-weighted liver imaging with simultaneous coil sensitivity estimation and reconstruction
[J].
RIRGAN: an end-to-end lightweight multi-task learning method for brain MRI super-resolution and denoising
[J].
Simultaneous superresolution reconstruction and distortion correction for single-shot EPI DWI using deep learning
[J].
DOI:10.1002/mrm.29601
PMID:36705077
[本文引用: 1]

Single-shot (SS) EPI is widely used for clinical DWI. This study aims to develop an end-to-end deep learning-based method with a novel loss function in an improved network structure to simultaneously increase the resolution and correct distortions for SS-EPI DWI.Point-spread-function (PSF)-encoded EPI can provide high-resolution, distortion-free DWI images. A distorted image from SS-EPI can be described as the convolution between a PSF function with a distortion-free image. The deconvolution process to recover the distortion-free image can be achieved with a convolution neural network, which also learns the mapping function between low-resolution SS-EPI and high-resolution reference PSF-EPI to achieve superresolution. To suppress the oversmoothing effect, we proposed a modified generative adversarial network structure, in which a dense net with gradient map guidance and a multilevel fusion block was used as the generator. A fractional anisotropy loss was proposed to utilize the diffusion anisotropy information among diffusion directions. In vivo brain DWI data were used to test the proposed method.The results show that distortion-corrected high-resolution DWI images with restored structural details can be obtained from low-resolution SS-EPI images by taking advantage of the high-resolution anatomical images. Additionally, the proposed network can improve the quantitative accuracy of diffusion metrics compared with previously reported networks.Using high-resolution, distortion-free EPI-DWI images as references, a deep learning-based method to simultaneously increase the perceived resolution and correct distortions for low-resolution SS-EPI was proposed. The results show that DWI image quality and diffusion metrics can be improved.© 2023 International Society for Magnetic Resonance in Medicine.
Denoising diffusion probabilistic models
[J].
Diffusion models in medical imaging: a comprehensive survey
[J].
DDM2: self-supervised diffusion MRI denoising with generative diffusion models
[J].
Fiberfox: facilitating the creation of realistic white matter software phantoms
[J].
DOI:10.1002/mrm.25045
PMID:24323973
[本文引用: 1]

Phantom-based validation of diffusion-weighted image processing techniques is an important key to innovation in the field and is widely used. Openly available and user friendly tools for the flexible generation of tailor-made datasets for the specific tasks at hand can greatly facilitate the work of researchers around the world.We present an open-source framework, Fiberfox, that enables (1) the intuitive definition of arbitrary artificial white matter fiber tracts, (2) signal generation from those fibers by means of the most recent multi-compartment modeling techniques, and (3) simulation of the actual MR acquisition that allows for the introduction of realistic MRI-related effects into the final image.We show that real acquisitions can be closely approximated by simulating the acquisition of the well-known FiberCup phantom. We further demonstrate the advantages of our framework by evaluating the effects of imaging artifacts and acquisition settings on the outcome of 12 tractography algorithms.Our findings suggest that experiments on a realistic software phantom might change the conclusions drawn from earlier hardware phantom experiments. Fiberfox may find application in validating and further developing methods such as tractography, super-resolution, diffusion modeling or artifact correction.Copyright © 2013 Wiley Periodicals, Inc.
The challenge of mapping the human connectome based on diffusion tractography
[J].