波谱学杂志, 2024, 41(2): 184-190 doi: 10.11938/cjmr20233080

研究论文

高性能铷原子钟的高精度频率漂移补偿研究

徐俊秋1,2, 李俊瑶1,2, 赵峰1, 康松柏1, 王鹏飞1, 明刚,1,*

1.中国科学院原子频标重点实验室（中国科学院精密测量科学与技术创新研究院），湖北 武汉 430071

2.中国科学院大学，北京 100049

High-precision Frequency Drift Compensation Study of High-performance Rubidium Atomic Clock

XU Junqiu1,2, LI Junyao1,2, ZHAO Feng1, KANG Songbai1, Wang Pengfei1, Ming Gang,1,*

1. CAS Key Laboratory of Atomic Frequency Standards (Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences), Wuhan 430071, China

2. University of Chinese Academy of Sciences, Beijing 100049, China

通讯作者: *Tel: 15927259500, E-mail:ming@apm.ac.cn.

收稿日期: 2023-09-7   网络出版日期: 2023-09-28

基金资助: 国家重点研发计划(2023YFC2205402)

Corresponding authors: *Tel: 15927259500, E-mail:ming@apm.ac.cn.

Received: 2023-09-7   Online: 2023-09-28

摘要

铷原子钟可靠性高、体积小、功耗低，在导航、通信等领域被广泛使用．尤其对于导航卫星星载铷原子钟，发展至今具有了优异的稳定度性能，但其固有的频率漂移特性（约E-12~E-13/天）会恶化其长期性能，影响卫星自主守时能力．通过对高性能铷原子钟的频率数据进行充分分析，评估可能导致频率漂移的物理机制，提出一种高精度频率漂移补偿的方案并开展了实验验证．结果表明，在无外部驯服情况下60天内高性能铷原子钟的漂移率可保持E-15/天量级，天稳定度达到E-15量级（Allan偏差），极大提升铷原子钟的自主守时能力.

关键词： 铷原子钟; 频率漂移; 漂移补偿; 自主守时

Abstract

With their high reliability, small size and low power consumption, rubidium atomic clocks are widely used in the fields of navigation, communication, etc. In particular, rubidium atomic clocks for navigation satellites have developed excellent stability. However, their inherent frequency drift characteristics (about E-12 to E-13/day) will deteriorate their long-term performance and affect the autonomous punctual timing of satellites. In this paper, we fully analyzed the frequency data of high-performance rubidium atomic clocks, aiming to figure out the physical mechanism behind the frequency drift. A high-precision frequency drift compensation scheme is proposed and experimentally verified. The results show that the drift rate of high-performance rubidium clock can be maintained in the order of E-15/day within 60 days without external taming, and the day stability can reach the order of E-15 (Allan variance), which greatly improves the autonomous punctual timing ability of rubidium atomic clock．

Keywords： rubidium atomic clock; frequency drift; frequency drift compensation; autonomous punctual timing

PDF (571KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

徐俊秋, 李俊瑶, 赵峰, 康松柏, 王鹏飞, 明刚. 高性能铷原子钟的高精度频率漂移补偿研究[J]. 波谱学杂志, 2024, 41(2): 184-190 doi:10.11938/cjmr20233080

XU Junqiu, LI Junyao, ZHAO Feng, KANG Songbai, Wang Pengfei, Ming Gang. High-precision Frequency Drift Compensation Study of High-performance Rubidium Atomic Clock[J]. Chinese Journal of Magnetic Resonance, 2024, 41(2): 184-190 doi:10.11938/cjmr20233080

引言

传统气泡型铷原子钟以其可靠性高、体积小以及功耗低的优势被广泛应用于导航、通信等领域[1].经过几十年的发展，铷原子钟频率稳定度性能得到了极大提升，但其频率漂移率仍然相对较大[2]，这制约了铷原子钟的长期性能，从而限制了应用范围的进一步拓展.本实验室用于导航卫星的甚高精度星载铷原子钟的中短期稳定度已经达到6.1E-13τ-1/2（τ=1~4 000 s），但长期稳定度却并不理想.影响铷原子钟长期稳定度性能的因素有环境敏感性和自身的频率漂移等.甚高精度铷原子钟经过有效的设计和合理的参数优化后，其环境敏感性对于长期稳定度的影响远低于铷原子钟自身的频率漂移率[3⇓-5].通过对比甚高精度铷原子钟的Allan偏差和Hadamard偏差（Hadamard偏差对频率数据进行了一次差分，可以扣除漂移率对于长期稳定度的影响），如图1所示，可以进一步判定频率漂移率是制约长期稳定度性能的主要因素.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   甚高精度铷原子钟的稳定度指标

Fig.1   Stability index of high-performance rubidium atomic clock


铷原子钟的频率漂移是自身的物理特性，一般表现为频率随时间单向变化，当加电时间足够长后，具有较高的线性度[6].目前对铷原子钟频率漂移率的控制有两种途径，一种是优化原子体系各种频移相关参数，但由于铷原子钟频率漂移率机理较为复杂[7]，该方案很难将漂移率优化至理想水平；另一种是对铷原子钟的频率漂移规律建立模型进行预报，然后对铷原子钟输出信号进行精确调频补偿，从而降低漂移率，这是目前被研究较多的一种方案.但其最好的结果也仅仅使得铷原子钟频率漂移率达到约5E-14/天的水平[8]. E-14/天量级的漂移率也远大于甚高精度铷原子钟扣除漂移率后的天稳定度（Hadamard偏差），严重制约了铷原子钟稳定度的提升，因此需要一套高精度频率的漂移补偿方案.

1 铷原子钟频率漂移模型

铷原子钟频率漂移可能由几种内在物理机制共同决定的：(1)抽运光功率衰减导致的光频移[9]；(2)微波腔内铷迁移导致腔内微波场分布变化引起的位置频移[10]；(3)氦气渗透导致的气体碰撞频移[11]；(4)抽运光光谱变化导致的光频移[12]；(5)缓冲气体氮气向泡壁缓慢扩散导致的气体碰撞频移[13]；(6)电子元器件老化[14]. 不同物理机制铷原子钟频率漂移的数学模型如下[15,16]：

1）氦气渗透、光强衰减——e指数模型与线性模型

$y=a+b * \mathrm{e}^{\frac{t}{c}}$
$y=a+b * t$

(1)和(2)式中y是输出频率，a是初始频率，t是时间，b是由各种物理机制导致的频率漂移率，c是常数，与氦气渗透的作用时间有关.氦气渗透符合e指数模型.氦渗透平衡过程会持续十多年，在较短的时间尺度内（数十天），线性度较高，可以用线性模型近似；在更长的时间尺度上非线性特征会明显表现出来.理论计算的氦渗透导致的频率漂移率在E-14/天甚至更低，这与玻璃材质以及初始时刻内外氦气压差有关.目前能证明频率漂移与氦气渗透有关，但是量级并不符合.

谱灯光强衰减本质上也符合e指数模型，但是光强衰减的平衡时间较短，通常在百天以内.在装机前谱灯会进行一段时间的老化处理，使光强达到稳定状态.在以年为单位的时间尺度上，光强的非线性特征才能明显表现出来，所以在时间尺度不是很长的情况下，光强衰减也可以用线性模型近似.理论评估光强衰减导致的频率漂移量比实际漂移量低了一个量级，所以光强衰减并不是频率漂移的主要原因.

2）缓冲气体扩散——扩散模型

$y=a+b * \sqrt{t+d}$

(3)式中y是输出频率，a是初始频率，t是时间，b是缓冲气体扩散导致的频率漂移率，d是常数，与缓冲气体扩散的作用时间有关.缓冲气体扩散是一种可能的影响机制，目前有氮气在500 ℃时会与玻璃发生反应的报道[17].但在铷原子钟工作时，氮气与玻璃的反应情况并没有相关报道.

3）电子元器件老化——对数模型

$y=a+b * \ln (t+c)$

(4)式中y是输出频率，a是初始频率，t是时间，b是由各种物理机制导致的频率漂移率，c是常数.电子元器件老化在铷原子钟的整个寿命内都会存在.但对于漂移的影响量级目前没有文献报道.

微波腔内铷迁移导致腔内微波场分布变化引起的频移以及光谱线型变化导致的频移，目前没有合适的数学模型能够描述.在实际工作中，铷原子钟内部不同物理机制共同作用使得其漂移率往往不遵从上述某一具体模型.基于可能的物理机制，通过设计出不同复合模型，可对铷原子钟的频率漂移做到更加精准的补偿.

2 频率漂移模型评估

取甚高精度铷原子钟一段长时间（>100天）测量的频率数据进行实验.通过比较不同模型预测结果，找到最适合的预测模型.

本文用到的几种复合数学模型如下：

1）双e指数模型

$y=a * \mathrm{e}^{\frac{t}{b}}+c * \mathrm{e}^{\frac{t}{d}}$

(5)式中y是铷原子钟的输出频率，a、c分别表示吸收泡和滤光泡的氦气渗透导致的漂移率；b、d为常数，t是时间.

2）线性-扩散模型

$y=a+b * t+c * \sqrt{t+d}$

(6)式中y是铷原子钟的输出频率，a是初始频偏，b是光强衰减导致的线性漂移率，c是缓冲气体扩散导致的漂移率，t是时间.

3）线性-对数模型

$y=a+b * t+c * \ln \sqrt{t+d}$

(7)式中y是铷原子钟的输出频率，a是初始频偏，b是光强衰减导致的线性漂移率，c是电子元器件老化带来的漂移率，d是常数，t是时间.

首先，利用几种复合数学模型对前40天的频率数据进行拟合，得到各种物理机制导致的频率漂移率参数.40天是使用稳健最小二乘法进行拟合达到拟合精度极限的最小数据量.利用拟合数据与测量频率数据的均方根误差来表示模型对于铷原子钟频率漂移规律的匹配程度.均方根越小，说明模型越匹配.然后，用40天后的实际测量频率与各个模型预测的频率作差，以15天为滑动窗口计算剩余线性漂移率.当线性漂移率未超出设定阈值（1.0E-14/天），认为模型预测的有效天数越多表明预测能力越好.剩余总漂移率是预测有效天数内的整体平均的线性漂移率，失效前剩余漂移率是最后一个15天窗口内的线性漂移率.不同复合模型的预测指标结果如表1所示，为了便于比较，表中加入了最常用的短期预测模型即线性模型预测指标.通过表1可见，线性-扩散模型表现最优，预测有效天数最多，且剩余总漂移率最低，因此，以此模型作为漂移补偿模型进行实验验证.

表1   不同模型预测指标

Table 1  The prediction parameters of different models

模型均方根预测的有效时长剩余总漂移率失效前剩余漂移率
线性模型8.27E-1320天6.3E-15/天9.4E-15/天
双e指数模型2.49E-1340天4.3E-15/天9.5E-15/天
线性-扩散模型3.13E-1460天3.8E-15/天9.4E-15/天
线性-对数模型3.06E-1335天4.7E-15/天9.3E-15/天

新窗口打开| 下载CSV


3 铷原子钟漂移补偿验证方案设计及实现

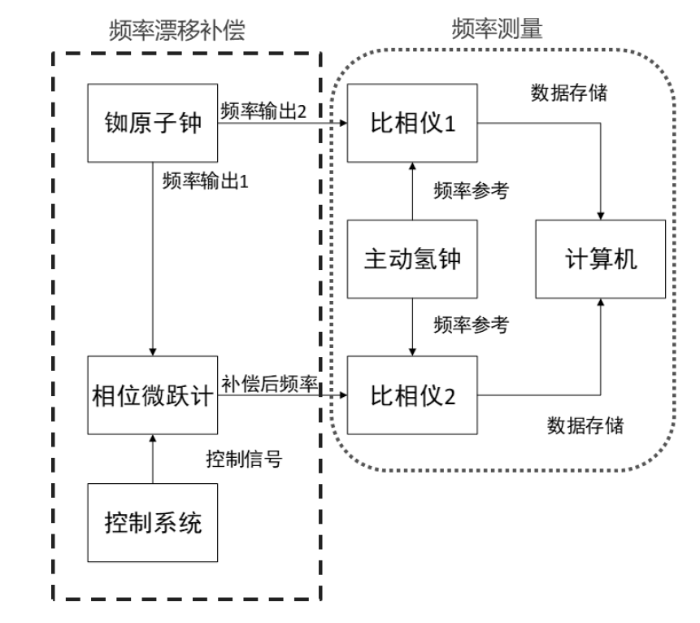
铷原子钟的频率漂移补偿以及验证方案包含频率漂移补偿和频率测量两个模块，如图2所示.频率漂移补偿是利用直接频率合成技术以铷原子钟的10 M信号为参考产生一个低频的补偿信号，再与铷原子钟的10 M信号混频得到补偿后的10 M信号.因为比相法测量精度高，频率测量采用的是比相法.铷原子钟的10 M频率信号分为两路，一路进行频率漂移补偿，另一路不进行频率漂移补偿.将补偿前后的两路频率信号分别与主动氢钟的10 M信号进行比较，得到对照的实验结果.监测补偿后频率变化是否与预期一致.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   铷原子钟漂移补偿实验框图

Fig.2   Block diagram of rubidium atomic clock drift compensation experiment


频率漂移补偿实现步骤如下：

1）利用40天甚高精度铷原子钟的频率数据计算线性-扩散模型的线性漂移率、扩散漂移率和起始频率.

2）将模型参数输入控制系统，控制系统计算出频率漂移补偿的单次频率补偿步进和补偿周期，并发送给相位微跃计.单次频率补偿步进需要远小于频率准确度，以免引起较大的频率阶跃，补偿周期需要考虑到频率补偿步进和补偿后的剩余残差，以免造成误差累积.

3）利用相位微跃计进行频率补偿并输出补偿后的频率.

4）监测补偿后的10 M信号，如果实测值的漂移率超过1E-14/天的阈值，则模型预测失效，需要重新修正参数.

本实验所使用设备主要有甚高精度铷原子钟（在开始本次实验前，已经加电运行6个月）、比相仪、主动氢钟和相位微跃计，相关性能参数如表2所示.经过计算分析，所使用设备的性能水平满足高性能铷原子钟的实验需求.

表2   实验设备性能

Table 2  Performance of experimental equipment

实验设备性能参数
VCH-314比相仪测量误差
1 s1.9E-14
10 s2.4E-15
100 s5.0E-15
1000 s8.6E-17
CH-75主动氢钟频率稳定度
1 s2.0E-13
10 s3.0E-14
100 s7.0E-15
1000 s3.0E-15
1天3.0E-16
漂移率<3.0E-16/天
相位微跃计调节精度1 pHz
调节范围1 Hz

新窗口打开| 下载CSV


4 实验结果

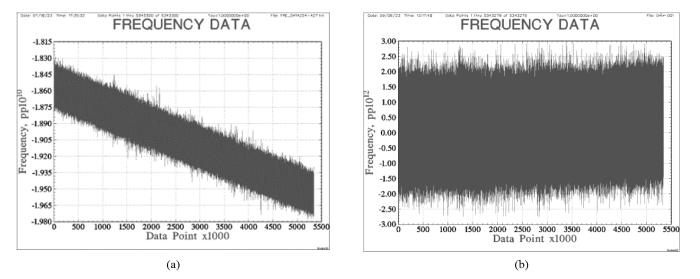
高精度频率漂移补偿实验在运行62天后，剩余漂移率达到阈值.Allan偏差评估天稳定度从1.3E-13提高到了6.0E-15，剩余平均漂移率4.0E-15/天，最后15天的平均漂移率为9.4E-15.补偿前后的频率输出实验结果如图3所示.频率补偿后，铷原子钟输出频率的准确度从E-10量级提高到了E-13量级，频率的漂移也明显变小，频率输出更加平稳，自主守时能力有了巨大提高.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   (a)原始频率输出；(b)补偿后频率输出

Fig.3   (a) Raw frequency output; (b) Frequency output after frequency drift compensation


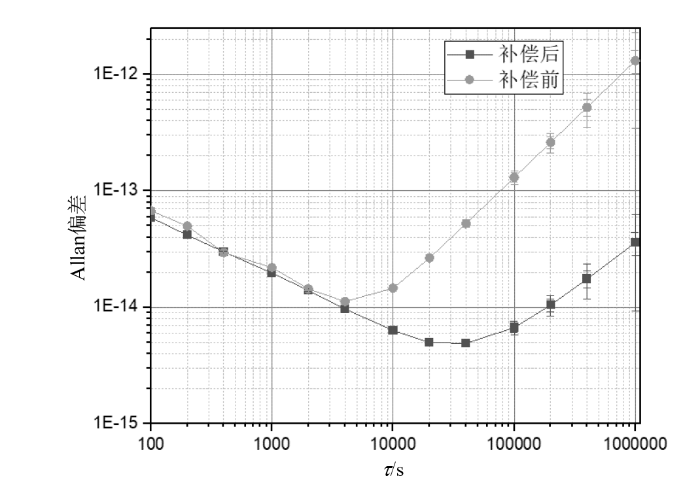
图4为补偿前后频率稳定度指标，即Allan偏差随时间的变化.可以看出，短期频率稳定度并没有恶化，为5.76E-13τ-1/2（τ=1~4 000 s），Allan偏差评估的天稳定度从补偿前的1.5E-13提高到了6.7E-15，稳定度提升了两个数量级，已经与Hadamard偏差评估的天稳定度达到同一量级，达到了实验预期.使用该技术后，铷钟在62天内的由频率漂移导致的守时误差为660 ns，频率准确度误差为1.65 μs，稳定度误差约为196.9 ns.在同一铷钟的同一寿命阶段内进行了多次补偿测试，天稳定度基本处在6.0E-15~7.0E-15的水平，漂移率都处在E-15/天量级，说明该技术方案具有一定的普适性.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   补偿前后频率稳定度

Fig.4   Frequency stability before and after compensation


5 总结

本文基于可能导致铷原子钟频率漂移的物理机制，利用复合模型预测铷原子钟频率漂移并设计方案与实验.结果表明，该方案可以在没有驯服的情况下，对铷原子钟中长期的频率漂移进行补偿，甚高精度铷原子钟的天稳定度从1.3E-13提高到了6.0E-15水平（Allan偏差评估）.虽然利用电子学手段不能彻底补偿频率漂移，但是能够在未来的中长期时间内把漂移率控制在一个较低的水平，且不恶化铷原子钟的稳定度.该方案极大提高了铷原子钟的自主守时能力，可以满足中长期的守时要求，拓展了铷原子钟的使用场景.

利益冲突

无

参考文献

MEI G H, ZHAO F, QI F, et al.

Characteristics of the space-borne rubidium atomic clocks for the BeiDou III navigation satellite system

[J]. Science China Physics, Mechanics & Astronomy, 2021, 51(1): 118-124. (in Chinese)

[本文引用: 1]

梅刚华, 赵峰, 祁峰, 等.

用于北斗三号卫星导航系统的星载铷原子钟特性

[J]. 中国科学: 物理学力学天文学, 2021, 51(1): 118-124.

[本文引用: 1]

JADUSZLIWER B, CAMPARO J.

Past, present and future of atomic clocks for GNSS

[J]. GPS Solut 2021, 25 (27): 1-13.

[本文引用: 1]

CUI J, MING G, WANG F, et al. Design and studies of an ultra high-performance physics package for vapor-cell rubidium atomic clock[C]// China Satellite Navigation Conference, Beijing, China: Springer, 2022, 910: 403-414.

[本文引用: 1]

LI J, MING G, ZHAO F, et al.

A rubidium atomic frequency standard with stability at 10-15 level operated under atmospheric condition

[C]// China Satellite Navigation Conference, Springer, 2021, 774:62-73.

[本文引用: 1]

HAO Q, LI W B, HE S G, et al.

A physics package for rubidium atomic frequency standard with a short-term stability of 2.4×10-13 τ-1/2

[J]. Rev Sci Instrum, 2016, 87(12): 123111.

[本文引用: 1]

郭海荣. 导航卫星原子钟时频特性分析理论与方法研究[D]. 解放军信息工程大学, 2006.

[本文引用: 1]

LIU C, XU F, QU Y, et al. Analysis on Factors Influencing Frequency Drift of Rubidium Clocks for Satellite Navigation[C]// China Satellite Navigation Conference, Changsha, China: Springer, 2016, 390: 645-652.

[本文引用: 1]

何冬, 赵明, 谢军, 等.

基于DDS的导航卫星钟频率漂移率的补偿方法

[C]// 第六届中国卫星导航学术年会论文集—S04原子钟技术与时频系统. 中国, 西安, 2015: 68-72.

[本文引用: 1]

CAMPARO J.

Does the light shift drive frequency aging in the rubidium atomic clock

[J]. IEEE T Ultrason Ferr, 2005, 52(7): 1075-1078.

[本文引用: 1]

COFFER J, SICKMILLER B, CAMPARO J.

Cavity Q aging observed via an atomic-candle signal

[J]. IEEE T Ultrason Ferr, 2004, 51(2): 139-145.

[本文引用: 1]

CAMPARO J, KLIMCAK C. Influence of the atmosphere on a rubidium clock’s frequency aging[C]// Conference:39th Annual Precise Time and Time Interval (PTTI) Meeting, Long Beach, CA: IEEE Xplore, 2007: 317-322.

[本文引用: 1]

CAMPARO J. Frequency equilibration and the light shift effect for block IIR GPS rubidium clocks[C]// Conference:36th Annual Precise Time and Time Interval (PTTI) Systems and Applications Meeting, Washington, D C: IEEE Xplore, 2004: 393-410.

[本文引用: 1]

RILEY W J. A history of the rubidium frequency standard. [2011-01-01]. https://ieee-uffc.org/presentation/history-rubidium-frequency-standard

URL     [本文引用: 1]

VANIER J, GAGNEPAIN J J, RILEY W J, et al. Aging, warm-up time and retrace: important characteristics of standard frequency generators[C]// Frequency Control Symposium, Hershey, PA, USA: IEEE, 1992: 807-815.

[本文引用: 1]

WANG P F, WANG F, ZHAO F, et al.

Performance analysis of BD III satellite rubidium atomic clock based on satellite-ground two-way time transfer data

[J]. Progress in astronomy, 2021, 39(4): 555-564.

[本文引用: 1]

王鹏飞, 王芳, 赵峰, 等.

基于星地双向时间比对数据的北斗三号铷原子钟在轨性能评估

[J]. 天文学进展, 2021, 39(4): 555-564.

[本文引用: 1]

CARLÉ C, KESHAVARZI S, MURSA A, et al.

Reduction of helium permeation in microfabricated cells using aluminosilicate glass substrates and Al2O3 coatings

[J]. J Appl Phys, 2023, 133 (21): 214501.

[本文引用: 1]

YASHCHISHIN I N, ZHUK L V, KOZII O I.

Diffusion processes in lead-silicate glasses in gas heat treatment with nitrogen

[J]. Glass & Ceramics, 2006, 63(11-12): 408-410.

[本文引用: 1]

/

〈 〉

网站设计版权所有 © 2017 《波谱学杂志》编辑部
地址：湖北省武汉市武昌区小洪山西30号 中科院精密测量科学与技术创新研究院波谱楼 《波谱学杂志》编辑部
邮编：430071　电话/传真：(086)027－87198791   E-mail: magres@wipm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发