引言
核磁共振技术是一种分析化合物结构的高效方法.这种技术不仅能在分子水平上分析物质的物理特性和功能,还具有无损检测的优势,能保持测试样本的完整性[1].这一特性使其被广泛应用于生物学、医学、有机化学等多个学科研究及工业领域中[2⇓-4].目前的高场核磁共振仪器体积较大,无法满足现场实时检测的要求[5].目前国内大部分高校实验设备均为大型谱仪,随着核磁共振波谱仪逐渐应用于化学教学实验中[6,7],谱仪的小型化有望实现谱仪以教具形式出现在高校实验室,推动高校核磁共振实验的普及.小型化核磁共振仪器的研究是核磁共振领域的一个研究热点.永磁体的发展促进了小型核磁共振波谱仪在医学和化学领域现场检测中的广泛应用[8].Halbach磁体结构因其永磁材料的高利用率和产生高场强的能力而被广泛应用于小型化核磁共振波谱仪中[8,9].然而,在磁体制造和组装过程中,离散化、不均匀磁化和误差等问题都会导致磁体的均匀性发生变化[10].这导致实际的磁场均匀度与理论计算值和仿真值之间存在巨大差异,通常相差2~3个数量级[11].因此,对磁体进行匀场处理至关重要.
目前也存在不依赖于铁磁片的无源匀场技术.Parker等人利用磁块的缺陷,在Halbach磁体中加入特定的磁块,从而实现了增强磁场均匀性[16].Tewari等人通过修改磁体中各个磁块的角度实现了Halbach磁体磁场均匀性的提高[17].Danieli等人开发了一种具有径向可移动磁块的Halbach磁体.这种设计可以根据球谐函数调整磁块的位置,从而校正谐波成分[18].在国内,东南大学团队通过在磁体外部放置相应的磁块抵消磁场的不均匀分量实现无源匀场[11];中国科学院电工研究所团队开发了一种独特的Halbach磁体配置,由偶极圆柱磁体和半球形磁体组成,旨在增强磁场的均匀性[19];浙江大学团队通过改变Halbach磁体中磁块尺寸、位置、堆栈结构等,对磁场均匀度进行仿真优化[20];东北电力大学团队通过改变磁块尺寸补偿端部效应实现无源匀场[21].
本文利用12个磁块设计了Halbach磁体阵列,磁场强度能够达到1.03 T.并且能够在装配完成后对磁块进行径向调整.随后建立一个均匀磁场作为优化的初始数据,选择实际测量的磁场作为优化目标,通过优化算法,确定12个磁块的径向反偏移距离.最后,根据优化结果调整Halbach磁体,证明了本文提出的无源匀场方法的有效性.
1 磁体设计
磁体设计的基本思路是将无磁材料和永磁材料结合,将永磁材料固定在无磁材料上,利用行进螺丝控制无磁材料的移动,进而控制永磁材料移动.
图1
图1
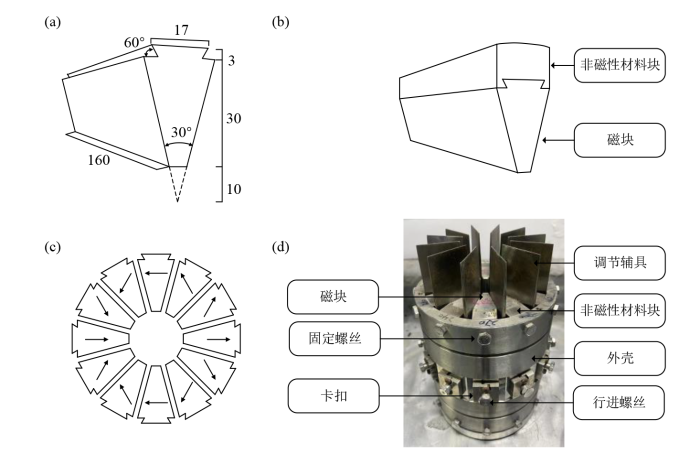
Halbach磁体的规格.(a)本文设计的磁块规格(单位:mm),(b)磁块与非磁性材料块之间的机械配合示意图,(c)永磁块的磁化示意图,(d)本文设计的Halbach磁体阵列整体示意图
Fig. 1
Specifications for Halbach magnet. (a) The magnetic block’s specifications designed in this study (given in mm). (b) The schematic diagram of the mechanical coordination between magnetic block and non-magnetic material block. (c) Schematic diagram of the magnetization mode of the permanent magnetic blocks. (d) Overall schematic of the Halbach array designed in this study
在由M个(M = 12)相同磁块组成的单极Halbach阵列中,每个磁块之间的夹角
为了确保磁体内部形成一个封闭的目标区域,本文使用非磁性金属材料设计了磁块阵列的外壳,从而为非磁性金属块和磁块提供支撑.外壳和非磁性金属块的配合是通过行进螺丝实现的.为了使磁块和非磁性金属块的径向移动与行进螺丝的旋转同步,必须将行进螺丝牢固地固定在外壳上.行进螺丝的紧固是通过使用专门为此设计的卡扣来实现的.当行进螺丝顺时针或逆时针旋转时,非磁性金属块因行进螺丝的固定位置而径向移动,从而带动磁块径向移动.另外,由于磁块间的磁力非常大,在安装时十分困难并且难以保证后续调节过程中磁块移动方向的精度.因此,本文设计了特殊辅具来协助安装和调节,辅具采用无磁材料制作,置于两磁块之间的缝隙中,保证匀场过程中磁块小范围的径向移动.本文设计的Halbach磁体阵列如图1(d)所示.
2 无源匀场优化设计
针对上述Halbach磁体设计,本文提出的无源匀场方法通过三步实现.首先是利用有限元分析软件确定静态理想磁场.在此过程中,材料的剩磁被设置为1.42 T.本文匀场的目标区域是位于磁体中心点、半径为2.5 mm的球体.其次,我们建立了磁块位置和磁场均匀性的数学问题.最后,采用优化算法得出磁块的位置偏差.在此过程中,理想的均匀磁场(12个磁块具有均匀的径向距离和圆周分布)被用作算法的初始值.该算法旨在优化磁场,使其与实际测量的磁场相匹配,而实际测量的磁场则是该算法的目标数据.该算法的输出是12个磁块的径向反偏移距离.
为了解决优化算法中目标函数未知的问题,即磁块的径向位置和磁场均匀性之间的关系未知,本文采用了有限元分析软件和数值计算软件结合的方法.通过有限元分析软件仿真得到数据构建相关矩阵,在数值计算软件中利用优化算法迭代得到最优解.
2.1 数值优化问题的建立
核磁共振系统的磁场符合拉普拉斯方程.因此,可以用球谐函数来表示磁场,它可以代表磁场的各种谐波成分.通过球谐函数得出的磁场用(1)式表示.
式中,
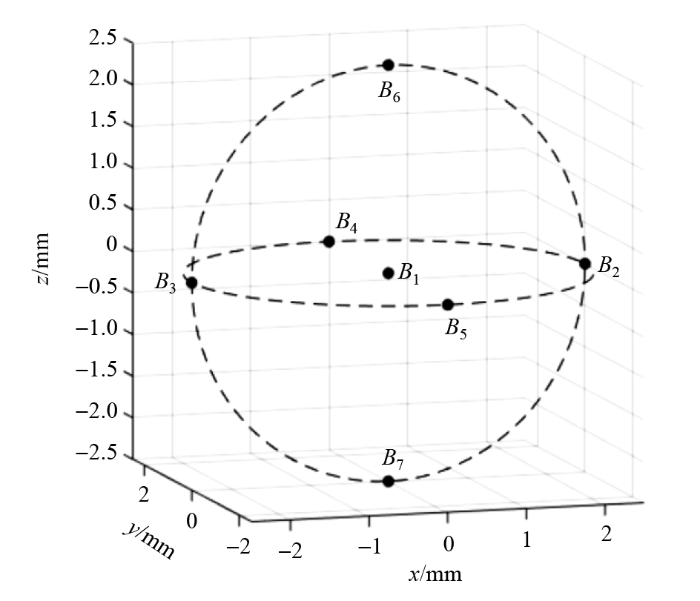
球谐函数的各个项之间具有完全的正交性,因此仅对有限的几个项进行匀场处理,而不会对其余的项产生影响.因此,本次研究的重点仅放在x、y和z轴的谐波分量上,目的是利用优化算法为Halbach磁体进行一阶匀场.本文测量了半径2.5 mm的球体上极角、方位角、距离相等的7个点处的磁场,采样点如图2所示.
图2
图2所示7个采样点的磁场分别为
磁场均匀性与磁块位置之间的关系可以用(3)式表示.
式中,
针对公式(3)中的非线性方程,本文构建了如(4)式所示的二范数
式中,H是根据实际测量磁场得出的磁场均匀度.
2.2 优化算法的实现
2.2.1 Levenberg-Marquardt方法的实现
在第2.1节中,我们建立了优化问题的数学模型,并将其归纳为最小二乘问题.本文选择Levenberg-Marquardt方法作为优化基础.因为所建立的数学模型没有提供有关磁块位置与磁场均匀性之间函数关系的信息,该方法可以利用Gram矩阵作为迭代中的一个参数,从而避免了计算Hessian矩阵的需要.同时,该方法还解决了Gauss-Newton法的局限性,即要求初始值接近最优解,以及梯度下降法的缺点,即容易陷入局部极小值.
因此,本文以(5)式为基础,引入了步长系数α,并随后推导出一个新的数学模型,用(6)式表示.
式中,
式中,J表示均匀度函数
值得注意的是,由于存在一个未知函数
在优化过程中,本文利用有限元分析软件对12个磁块的位置分别进行了微小的移动,并计算磁块位置移动对三个方向均匀度的改变,逐列填充Jacobian中元素.此外,为了保证优化程序的严谨性,在每次迭代开始时,都采用这种方法对Jacobian矩阵进行修正.
2.2.2 混合算法的实现
实验发现,仅使用Levenberg-Marquardt方法对磁体进行优化会导致线性收敛,而无法达到二次收敛,不能充分发挥该方法的优势.因此,本文采用了一种将Levenberg-Marquardt方法与拟牛顿法相结合的混合算法.拟牛顿法的加入有助于优化结果实现超线性收敛,从而提高优化性能.
混合算法以Levenberg-Marquardt方法作为初始迭代方法,如果连续三次迭代都满足(9)式,则转换到拟牛顿法.
式中,其中
拟牛顿法的基础是用矩阵B替代当前位置参数p的Hessian矩阵.其迭代步长由(10)式给出
式中,
近似矩阵B通过BFGS策略进行更新,且每次迭代中都是对称和正定的,从而保证
式中,
然而,拟牛顿法在迭代的全局阶段不够鲁棒,不能保证
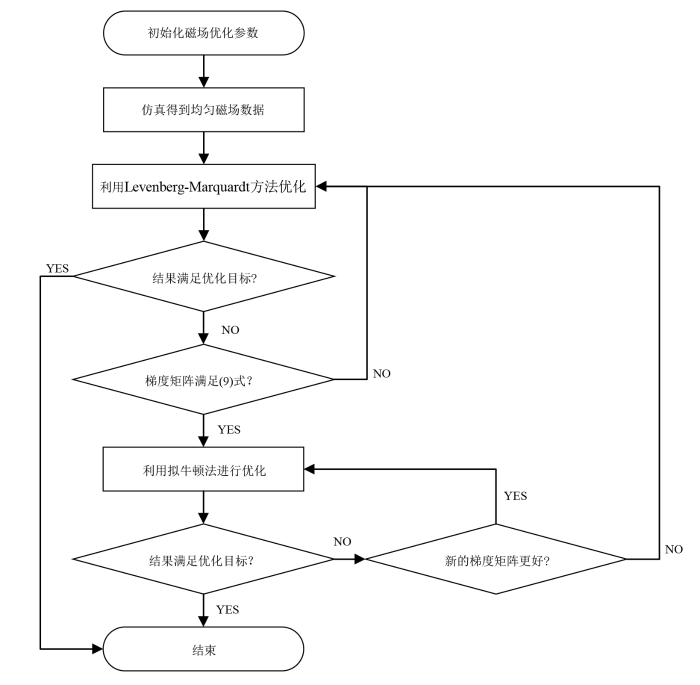
混合算法的流程如图3所示.
图3
图3
基于混合算法的无源匀场方法流程图
Fig. 3
Flowchart for optimal passive shimming solution by hybrid algorithm
3 结果与讨论
为了验证本文提出的方法的正确性,本文构建了一个仿真模型得到均匀磁场数据并测试实际加工得到的磁体的磁场.本文首先将第2节中设计建模的磁体结构导入有限元分析软件并为仿真设定适当的参数.在这一过程中,每个磁块需均匀磁化且剩磁大小相等,偶极矢量完全对齐,磁块的位置近似于Halbach设计,从而可以获得理想的均匀磁场.
为了保证磁场测量的精度,本文为此设计了一个测试平台.图4展示了本文设计磁场测量平台,其中包括一个三维高精度高斯计(Model-3600,北京翠海佳诚磁电科技)和一个三维移动设备.
图4
根据测量数据,可以计算出本文中制作的Halbach磁体目标匀场区域的平均磁场为1 037.754 mT(由于每个磁块之间存在间隙,主磁场与磁块的剩磁相比有所减弱),磁场偏差
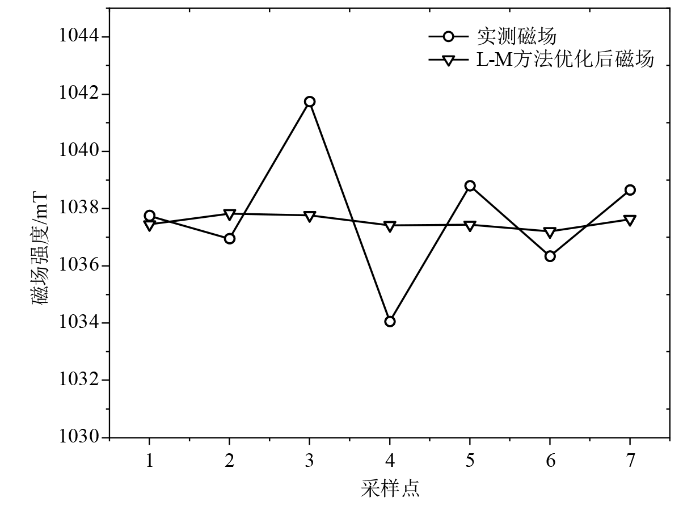
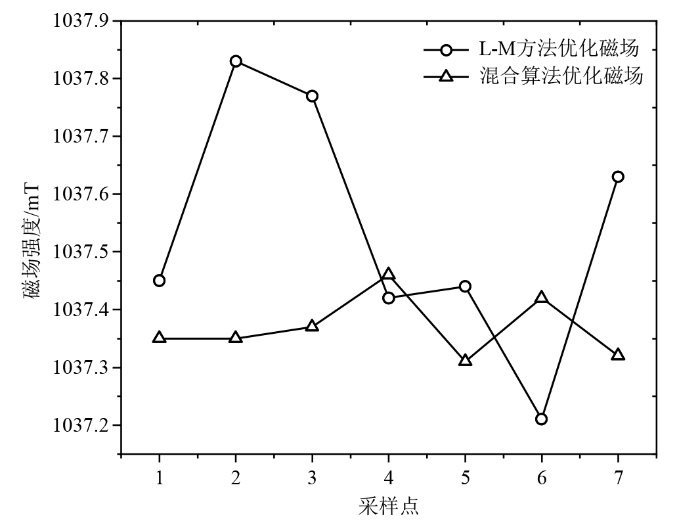
图5为利用Levenberg-Marquardt方法优化得到的磁场.从图中可看出,经过Levenberg-Marquardt方法进行优化后,磁场的均匀度有了一定的提升,从7 391 ppm(×10-6)提升到597 ppm.随后,我们利用混合算法进行磁场优化.混合算法优化结果与Levenberg-Marquardt方法优化结果的比较如图6所示.从图中可以看出,采用本文所述的混合优化算法后,中心直径为2.5 mm的磁球内均匀性显著提高.具体来说,均匀度从597 ppm提升到154.23 ppm.优化前后,磁块位置、磁体口径以及均匀度的变化如表1所示.表中径向移动距离正值为径向向外运动,而负值表示存在径向向内运动.
图5
图5
Levenberg-Marquardt优化前后的磁场对比图
Fig. 5
Comparison of magnetic fields before and after the Levenberg-Marquardt optimization
图6
图6
Levenberg-Marquardt方法和混合算法优化磁场对比图
Fig. 6
Comparison of magnetic fields optimized by Levenberg-Marquardt method and hybrid algorithm
表1 匀场前后数值变化对比表
Table 1
| 参数 | 匀场前 | 匀场后 |
|---|---|---|
| 磁块1径向移动距离 | 0 mm | -1.13 mm |
| 磁块2径向移动距离 | 0 mm | +0.76 mm |
| 磁块3径向移动距离 | 0 mm | -0.35 mm |
| 磁块4径向移动距离 | 0 mm | +0.53 mm |
| 磁块5径向移动距离 | 0 mm | -0.48 mm |
| 磁块6径向移动距离 | 0 mm | -1.25 mm |
| 磁块7径向移动距离 | 0 mm | -0.45 mm |
| 磁块8径向移动距离 | 0 mm | +1.20 mm |
| 磁块9径向移动距离 | 0 mm | +1.34 mm |
| 磁块10径向移动距离 | 0 mm | +0.85 mm |
| 磁块11径向移动距离 | 0 mm | -1.96 mm |
| 磁块12径向移动距离 | 0 mm | -1.40 mm |
| 磁体口径 | 30 mm | 27.6 mm |
| x方向均匀度 | 4 571 ppm | 19.2 ppm |
| y方向均匀度 | 4 601 ppm | 144.3 ppm |
| z方向均匀度 | 2 226 ppm | 106.03 ppm |
| 区域均匀度 | 7 391 ppm | 154.23 ppm |
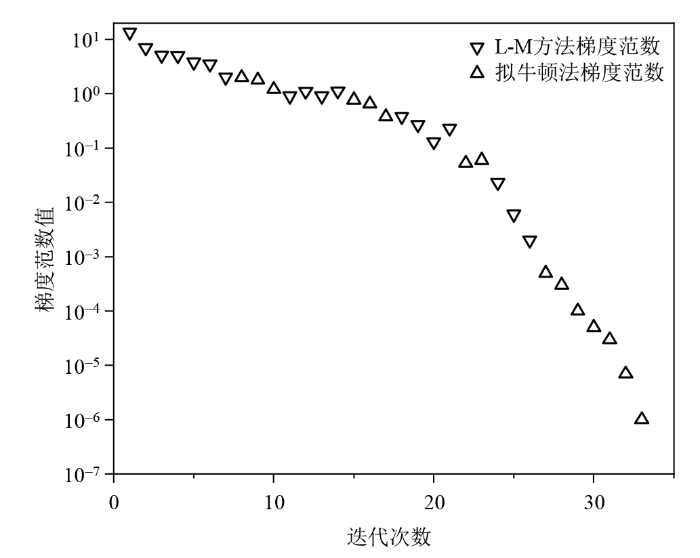
为了了解引入拟牛顿法对Levenberg-Marquardt方法的具体影响,图7显示了混合算法迭代过程中的梯度范数变化.
图7
图7
迭代过程中梯度范数变化图
Fig. 7
Changes of the gradient norm during the iterative process
从图7中可以看出,混合算法以Levenberg-Marquardt方法开始优化.在第8~10次、第15~17次迭代中,利用拟牛顿法进行优化,但范数下降速度不够快,因此切换至Levenberg-Marquardt方法;在第22~23次拟牛顿法迭代中,范数增大,在第24次切换至Levenberg-Marquardt方法.在第27次后的迭代中,范数均以较快的速度下降,利用拟牛顿法继续进行优化,最终实现了收敛.这一过程证明了本文在Levenberg-Marquardt方法中引入的拟牛顿法是有效的.
4 结论
本文研制了一种具有特殊机械结构的Halbach磁体.这种特殊的磁体结构能够在磁体组装过程完成后,利用行进螺丝改变磁块的径向位置进行无源匀场.针对这种结构,本文提出了一种结合了Levenberg-Marquart方法和拟牛顿法的无源匀场算法,成功地增强了Halbach磁体主磁场的均匀性,将均匀度从7 391 ppm提升到154.23 ppm.这表明本文提出的磁体结构及与之匹配的算法具有显著提高磁场均匀性的潜力.
然而,由于磁块之间存在间隙,主磁场强度会降低.因此,可以从增加磁体的磁场强度、温度稳定性和均匀性进一步优化磁体.可以通过增加磁体阵列的外部尺寸以获得更强的磁场.在温度稳定性方面,由于钐钴材料的热稳定性优于Nd2Fe14B,因此在磁体设计中使用钐钴材料可以在一定程度上提高磁体的温度稳定性.虽然,本文只关注一阶磁场的无源匀场应用,但本文讨论的技术有可能扩展到高阶磁场的优化.此外,采用少量有源匀场线圈可有效降低磁场的不均匀性,并解决机械运动精度带来的限制.
综上所述,本文提出了一种新的无源匀场方法,这种方法相较于传统无源匀场方法具有更高的灵活性和效率,为未来高分辨率核磁共振波谱仪的发展提供了一种前景广阔的磁体设计策略.
利益冲突
无
参考文献
Forty years of progress in nuclear magnetic resonance spectroscopy
[J].
Miniaturization of NMR systems: Desktop spectrometers, microcoil spectroscopy, and ‘NMR on a chip’ for chemistry, biochemistry, and industry
[J].
Magnetic field locking system based on fluxgate and time domain digital frequency discrimination
[J].
基于磁通门和时域数字鉴频的磁场锁定系统
[J].
A new method and circuit of ringing suppression for low-field NMR instruments
[J].
低场核磁共振仪器振铃抑制新方法及其电路实现
[J].
DOI:10.11938/cjmr20223002
[本文引用: 1]

加快天线残余能量释放以减弱天线振铃信号有利于缩短低场核磁共振仪器的回波间隔(TE),从而提高快弛豫组分的测量分辨率和信噪比(SNR).而天线Q值对能量的发射效率和泄放速度起着相反的作用.为此,我们首先设计了一种新型Q转换电路,在保证发射效率的同时,可以大大缩短能量泄放时间.在此基础上,应用了一种优化的脉冲序列以弥补传统相位交替对脉冲序列(PAPs)不能消除90°脉冲振铃的缺陷,通过相位循环的方法进一步提高了信噪比.最后,在2 MHz岩心分析仪上测试了新型Q转换电路,当天线Q值降为发射期间的约1/5时,天线恢复时间由280.0 μs降为18.2 μs;而且,使用新型Q转换电路和优化的脉冲序列后,TE=60 μs时,可以有效获得快弛豫组分的T<sub>2</sub>信号.
Limits to magnetic resonance microscopy
[J].
Exploration of the application of NMR technique in experimental teaching for undergraduates
[J].
核磁共振技术应用于本科实验教学的探究
[J].
Application of nuclear magnetic resonance spectroscopy in open experiment teaching
[J].
核磁共振波谱仪在开放实验教学中的应用
[J].
Design of permanent multipole magnets with oriented rare earth cobalt materials
[J].
An NMR relaxation method of characterizing hydrogen-bearing crystalline solid phases in hydrated cement paste
[J].
Magnetic field homogeneity perturbations in finite Halbach dipole magnets
[J].
Design and shimming method of low length-to-interdiameter ratio Halbach magnet
[J].
Active shimming method for a 21.3 MHz small-animal MRI magnet
[J].
Design and implementation of low-field NMR main magnet based on Halbach structure
[J].
基于Halbach结构的低场核磁共振主磁体的设计与实现
[J].
A passive shimming method for Halbach magnet based on magnetic sheet arrays
[J].
Shimming Halbach magnets utilizing genetic algorithms to profit from material imperfections
[J].
DOI:10.1016/j.jmr.2016.01.014
PMID:26874333
[本文引用: 1]

In recent years, permanent magnet-based NMR spectrometers have resurfaced as low-cost portable alternatives to superconducting instruments. While the development of these devices as well as clever shimming methods have yielded impressive advancements, scaling the size of these magnets to miniature lengths remains a problem to be addressed. Here we present the results of a study of a discrete shimming scheme for NMR Mandhalas constructed from a set of individual magnet blocks. While our calculations predict a modest reduction in field deviation by a factor of 9.3 in the case of the shimmed ideal Mandhala, a factor of 28 is obtained in the case of the shimmed imperfect Mandhala. This indicates that imperfections of magnet blocks can lead to improved field homogeneity. We also present a new algorithm to improve the homogeneity of a permanent magnet assembly. Strategies for future magnet construction can improve the agreement between simulation and practical implementation by using data from real magnets in these assemblies as the input to such an algorithm to optimize the homogeneity of a given design. Published by Elsevier Inc.
Improving the field homogeneity of fixed-and variable-diameter discrete Halbach magnet arrays for MRI via optimization of the angular magnetization distribution
[J].
Small magnets for portable NMR spectrometers
[J].DOI:10.1002/anie.201000221 PMID:20446281 [本文引用: 1]
Design and analysis of the novel test tube magnet as a device for portable nuclear magnetic resonance
[J].