引言
氢原子钟的原子弛豫时间是原子系统经过选态去除基态超精细能级(F = 0,mF = 0)态和(F = 1,mF = −1)态原子后,部分氢原子从(F = 1,mF = 0)态跃迁至(F = 0,mF = 0)态直至原子系统达到平衡状态所需的时间.
一方面,原子的弛豫时间反映了纯态原子的实际寿命,影响了原子能量状态和原子共振谱线的宽度.弛豫过程都有两种机制:一是与能级粒子数变化相联系的,表征能级之间布居数之差,其弛豫时间用T1表示;另一种与原子磁矩的衰减有关,称为横向弛豫,其弛豫时间用T2表示,它表征原子磁矩与辐射场的相干寿命[1].
另一方面,原子弛豫时间直接影响氢原子钟的稳定度指标.主动型氢原子钟的中长期频率稳定度理论计算公式为[2]:
(1) 式中,k为玻尔兹曼常数;T为热力学温度;
其中
本文通过Raspberry Pi(RPI)控制探测微波信号的输入,测量在不同激励条件下的氢原子受激辐射表现,通过检波电路和计算机,进行衰减信号的采集和拟合,从而实现了原子弛豫时间T1、T2的测量.相比较传统方法,使用RPI控制探测微波信号具有输入通用性好、实验过程简便的优势,同时可以根据不同氢原子钟的状态实时更改时序信号.
1 实验原理
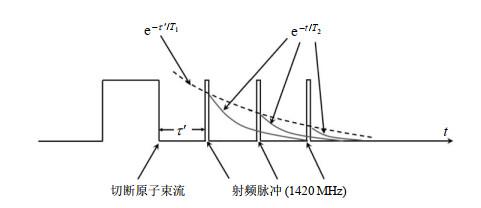
实验中先将氢原子束流关闭,经过
图1
关闭微波脉冲后,腔内的归一化磁感应振幅将逐渐衰减,衰减过程如(3)式所示[3].其中,
当微波脉冲结束时,t = 0,则腔内的微波磁感应的归一化振幅b(0)为[3]:
如图 1所示,改变注入微波信号与氢原子束关闭的间隔时间
由(4)式知,当微波脉冲为π/2脉冲时,即:
此时原子的跃迁几率最大.设微波脉冲的宽度
其中,
其中,
当
在原子达到平衡态后,关闭原子束流,注入功率为−59.2 dBm、时长为20 ms的微波脉冲信号,可以得到原子自由感应衰减信号.通过对信号进行数值运算,按照(3)式进行拟合,即可以得到原子弛豫时间T1、T2.
2 实验测量平台搭建
本实验通过RPI产生时序信号,控制数字衰减器和电离源供电电路的继电器从而控制微波探测信号的开启和原子束流的通断,与数据采集等电路,组成了氢原子自由感应衰减测试系统.通过对采集的自由感应衰减信号建模拟合,测算了氢原子钟的弛豫时间.
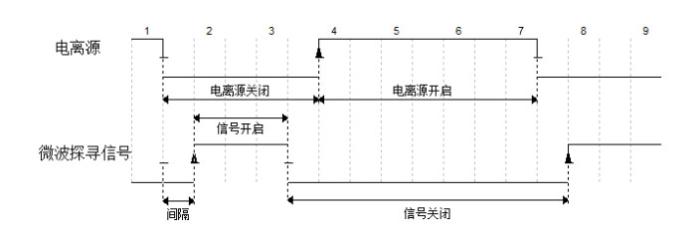
微波脉冲信号与原子束流的时序控制通过RPI来实现.将一个继电器串联接入电离源供电电路中,通过控制电离源的开关以控制原子束流的通断.微波信号综合器产生1.42 GHz微波信号,其输出端串联四个数字衰减器衰减值为123 dB,控制微波信号通断,型号为HMC273MS10G.通过调整微波信号综合器的输出频率、输出功率和数字衰减器的工作时序,即可生成π/2脉冲.当数字衰减器关闭时,微波脉冲有效的激励原子系统;当数字衰减器打开时,入腔微波信号低于−120 dBm,对原子系统无影响,等效于关闭探寻信号.电离源与微波脉冲信号的时序状态如图 2所示.
图2
图2
电离源和微波探寻信号的控制时序
Fig.2
Control timing of ionization source and microwave signal
图3
图3
氢原子自由感应衰减测试原理图
Fig.3
Schematic diagram of the free induction decay test of hydrogen atoms
3 实验结果与分析
氢原子系综弛豫跃迁信号经放大、下变频、模数转换测量.测试并调节各个模块的输出,使其符合自由感应衰减测量的条件.
3.1 T2的测量和评估
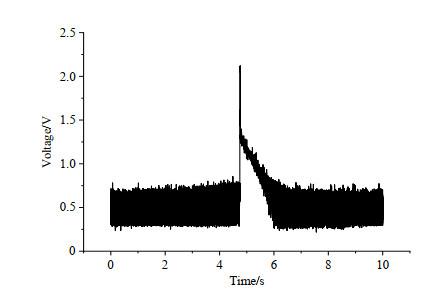
当实验中镍管加热电流为3A,输入功率为−60 dBm、脉冲持续时间τ = 0.02 s的脉冲时,满足
图4
图4
测量T2时的氢原子自由感应衰减信号
Fig.4
Free induction decay signal of hydrogen atom when measuring T2
此时功率信号表征为AD8307输出电压值,在数据处理阶段将此电压值按照对数格式转化为功率值,再通过数值运算转换为幅度值
图5
图5
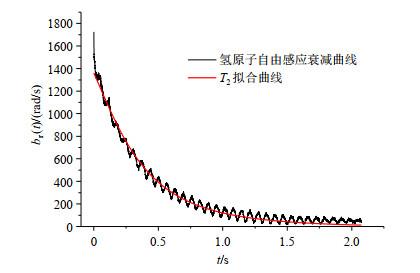
氢原子横向弛豫时间T2的拟合
Fig.5
Fitting for the transverse relaxation time T2 of hydrogen atom
表1 原子束流强度与T2关系
Table 1
| 镍管加热电流/A | T2/s | 原子线宽/Hz | 不确定度 |
| 3.0 | 0.5739±0.0061 | 0.5549±0.0058 | 1.06% |
| 2.3 | 0.6351±0.0251 | 0.5014±0.0190 | 3.93% |
| 1.5 | 0.7351±0.0312 | 0.4332±0.0448 | 4.24% |
在保证氢原子跃迁信号强度的前提下,适当减少氢原子流量对T2和原子共振线宽是有益的.束流的减少会导致原子辐射寿命的延长,使原子谱线变窄,但过小的原子束流也会影响氢原子钟的输出功率.因此,氢原子钟的束流强度需要根据具体系统状态进行优化.
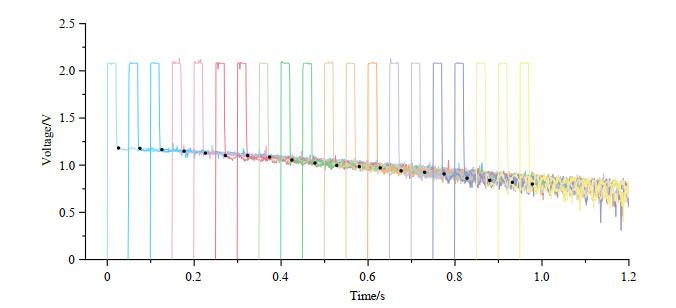
3.2 T1的测量和评估
图6
图6
测量T1时的氢原子自由感应衰减信号
Fig.6
Free induction decay signal of hydrogen atom when measuring T1
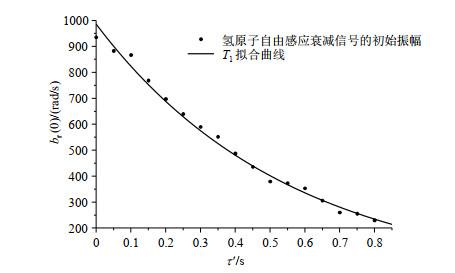
取每次脉冲结束时自由感应衰减信号的初始振幅值(此时t = 0)作为有效数据,此时的信号为AD8307输出的电压值,在数据处理阶段将此电压值按照对数格式转化为功率值,再通过数值运算转换为幅度值
图7
图7
氢原子纵向弛豫时间T1的拟合
Fig.7
Fitting for the longitudinal relaxation time T1 of hydrogen atom
4 结论
氢原子钟原子储存泡内的氢原子弛豫时间是影响氢脉泽信号线宽与功率,以及氢钟频率稳定度的关键参数.本文搭建了氢原子弛豫时间测试系统,在此基础上开展不同条件下的弛豫时间测量,并分析了测试结果.当镍管加热电流为3 A时,原子束流强度较大,T1约为0.556 0 s,T2约为0.573 9 s,与文献[3]给出的经验值吻合.改变镍管加热电流从而改变原子束流强度,并重新测量T2,得到T2随原子束流的减少而增大,测量结果与理论相符.原子弛豫时间测量系统的搭建具有普适性,可根据不同氢原子钟状态灵活设置参数测量,对后续改进氢原子钟原子线宽和性能指标有重要的参考意义.
无
参考文献
Theory of the hydrogen maser
[J].DOI:10.1103/PhysRev.126.603 [本文引用: 2]
Duration of hydrogen-atom spin-exchange collisions
[J].DOI:10.1103/PhysRevA.12.1305 [本文引用: 1]
Stimulated emission in the hydrogen maser and the H spin-exchange cross section
[J].
小型化氢脉泽原子储存时间设计
[J].
Design of the atomic storage time of a miniaturized hydrogen maser
[J].
脉冲微波激发氢原子Ramsey干涉研究
[J].DOI:10.3969/j.issn.1000-4556.2013.03.006 [本文引用: 1]
Induction of hydrogen Ramsey interference with pulsed microwave
[J].DOI:10.3969/j.issn.1000-4556.2013.03.006 [本文引用: 1]