引言
铷原子频标具有稳定度高、体积小、易携带等优点,广泛应用于导航、通信、航空航天等领域[1]. 铷原子频标是一个以物理系统为鉴频器的锁频环路,其将晶体振荡器(晶振)输出频率锁定在稳定的原子跃迁频率上,使晶振具有与铷原子跃迁频率相同的中长期频率稳定度,同时短期频率稳定度由晶振决定[2].晶振为铷原子频标提供初始频率源,同时也是标准频率输出的载体.晶体振荡器通常分为四类:普通晶体振荡器、压控晶体振荡器、温度补偿晶体振荡器、恒温晶体振荡器.其中,前三种类型晶体振荡器在性能上无法达到星载原子频标频率稳定度需求,而恒温晶体振荡器被认为是目前稳定度最好的振荡器,利用精密的控温电路和恒温结构保持晶体温度的恒定,因此其稳定度相比其它类型晶振有大幅度提高,被广泛应用于航空航天、精密测量等领域.
目前国内能生产研制高性能晶体振荡器的研究单位较少,其产品性能也与国外有一定差距;同时国外高性能宇航级产品不仅价格十分昂贵,且对国内有着严格的出口限制.目前应用于铷原子钟的一款典型国产晶体振荡器为中国电子科技集团公司第十三研究所研制的OXLN5x系列晶体振荡器,其尺寸大小为50 mm×50 mm×16 mm,相位噪声指标为:−102 dBc/Hz@1 Hz、−135 dBc/Hz@10 Hz、−150 dBc/Hz@100 Hz、−161 dBc/Hz@1 kHz,其相位噪声性能指标良好,但体积无法满足小型化星载铷原子频标要求.本文旨在设计一种小型化恒温晶体振荡器以满足应用需求.通过对Leeson模型[3]进行分析,利用射频仿真软件ADS优化仿真并指导设计电路;同时通过一系列方法,在满足性能需求前提下缩小晶体振荡器体积,最终实现了一种小型化低相噪恒温晶振,相位噪声指标约为:−103 dBc/Hz@1 Hz、−131 dBc/Hz@10 Hz、−150 dBc/Hz@100 Hz、−160 dBc/Hz@1 kHz,相位噪声性能与OXLN5X系列晶振相当,但体积仅为其五分之一,完全满足小型化星载铷原子频标需求.
1 晶体振荡器工作原理
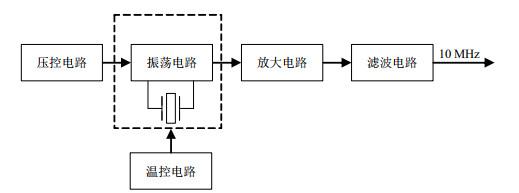
本文设计的晶体振荡器工作原理方框图如图 1所示,由振荡电路、放大电路、滤波电路、温控电路和压控电路构成.因SC切型石英谐振器可承受激励电平较大,短期频率稳定度好,且温度稳定性较高,故本文选用高Q值SC切3次泛音石英晶体,通过振荡电路产生10 MHz信号,再经放大电路增强振荡信号幅度,确保振荡器输出信号功率满足需求,最后通过滤波电路抑制信号谐波,减小负载牵引.温控电路的作用是将石英晶体的温度控制在晶体频率-温度特性曲线拐点处,减小压控晶振受外界温度变化的影响,改善晶体振荡器频率稳定性,压控电路通过外加电压微调晶体外部电容,对晶振频率进行控制.
图1
2 晶体振荡器电路设计
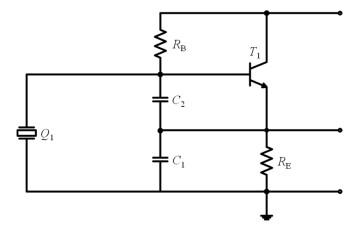
2.1 振荡电路设计
图2
图3
电路振荡方程为:
上式中实部为0,可得外电路的负电阻为:
其中,
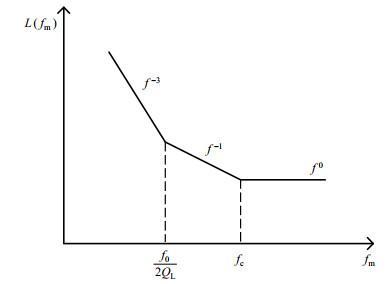
2.2 电路相位噪声优化设计
其中F为噪声系数,k为玻尔兹曼常数,T为绝对温度,
图4
由(3)式可知,振荡器相位噪声与噪声系数、输入信号功率、拐角频率以及品质因数有关,在设计电路时选择低噪声系数器件、增大信号功率、提升回路品质因数,有助于降低晶体振荡器相位噪声.
2.3 ADS仿真设计
图5
图5
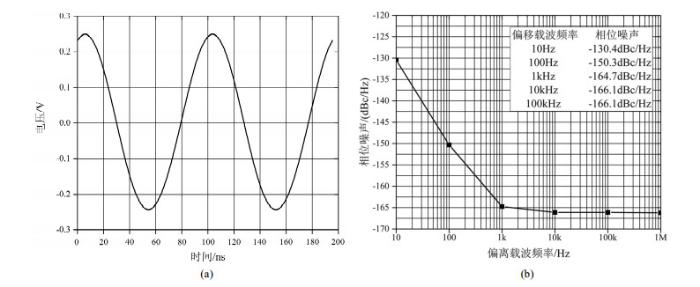
(a) 振荡电路输出信号波形仿真图;(b)振荡电路输出信号相位噪声仿真图
Fig.5
(a) Waveform simulation diagram of output signal of oscillator circuit; (b) Phase noise simulation diagram of output signal of oscillator circuit
2.4 放大电路及滤波电路设计
本文所设计晶体振荡器放大电路由两级构成:第一级采用共集放大电路;第二级采用共射放大电路,该级电路在放大信号功率同时可减小负载的牵引效应,提升晶体振荡器的隔离能力和频率稳定度.设计放大电路时应选择低噪声系数晶体管,并使晶体管工作在线性放大区内,在保证放大电路不产生失真的情况下,适当调整静态工作点以减小晶体管带来的噪声影响.后级滤波电路采用三阶切比雪夫低通滤波器,起到抑制谐杂波、提高信号频谱纯度作用,放大电路及滤波电路原理如图 6所示.
图6
图6
放大电路和滤波电路原理图
Fig.6
Schematic diagram of amplifier circuit and filter circuit
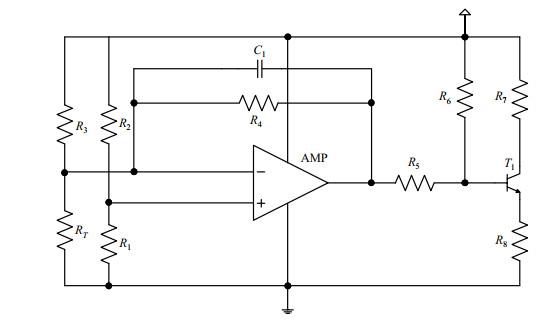
2.5 温控电路设计
图7
2.6 小型化与抗干扰设计
本文所设计电路在满足性能指标前提下,去掉增益控制电路,不仅简化了电路设计,使得调试难度降低,有利于晶振小型化设计,同时增加了电路整体稳定性,且避免增益控制电路带来的相位噪声恶化.选取小体积LDO电源芯片,表贴封装电阻、电容等元器件减小电路元件体积.采用四层板电路设计,提高布局布线密度,减小电路板面积.采用对晶体直接进行加热方案,减小晶振整体尺寸,最终实现小型化低噪声恒温晶体振荡器设计,晶振实物及封装尺寸如图 8所示.
图8
图8
(a) 10 MHz晶振实物图;(b) 10 MHz晶振封装尺寸图
Fig.8
(a) Picture of 10 MHz crystal oscillator; (b) Contour dimensional drawing of 10 MHz crystal oscillator
在元器件布局时注意按照信号流向关系,进行布线时避免走线过长,且避免锐角或者直角设计的出现.适当加宽电源线和地线,做到就近接地,并在电源芯片引脚与地线之间放置合适的去耦电容,同时增加一层完整的地平面,这些措施有利于提高晶体振荡器电磁兼容性能.将控温电路中的热敏电阻、功率三极管与晶体放置在背面并尽可能贴在一起,减少热量传递过程中的损耗,同时避免温度过高对振荡电路晶体管带来的影响.
3 性能测试及结果分析
本文所设计的低噪声10 MHz晶体振荡器,在完成了各部分电路的加工制作、实验调试及参数优化后能实现长期加电连续稳定的工作.为了对晶振的性能进行评估,本文分别在时域和频域对该晶体振荡器的性能进行了测试.
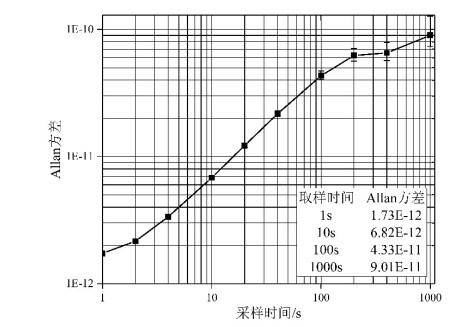
首先,本文以CH1-75A氢原子钟(短期频率稳定度为1.5×10−13/s)作基准参考源,用Picotime频率稳定度测试仪对该晶体振荡器的时域特性即频率稳定度(Allan方差)进行了测试,频率稳定度的实测结果如图 9所示. 其短期频率稳定度秒稳为1.73×10−12/s,该稳定度指标已达到小型化高稳恒温晶振水平.
图9
图9
10 MHz晶振Allan方差测试图
Fig.9
Allan deviation test plot for 10 MHz crystal oscillator
其次,本文用ROHDE & SCHWARZ FSW26频谱分析仪(无需外接参考源)对晶振各频点输出功率谱进行了测试,测试结果如图 10所示.当参考电平为20 dBm时,最终测得基频谐振功率为8.16 dBm,二次谐波抑制为−41.39 dB,达到本文设计需求.
图10
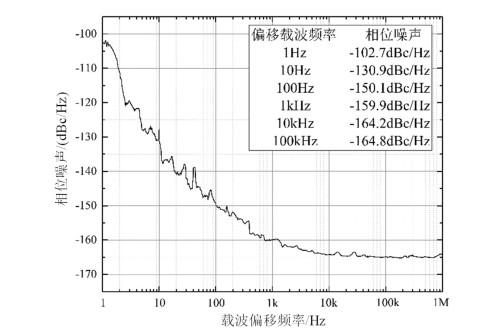
最后,本文用ROHDE & SCHWARZ FSWP26相位噪声分析仪(采用双通道互相关技术,因此无需外接参考源)对该晶体振荡器的频域特性相位噪声进行了测试,相噪测试结果如图 11所示.测试结果表明,该晶体振荡器具有良好的相噪特性,其近端相噪为−102.7 dBc/Hz@1 Hz、远端相噪为−164.2 dBc/Hz@10 kHz.
图11
图11
低噪声10 MHz晶振相位噪声测试曲线
Fig.11
Phase noise test plot of low noise 10 MHz crystal oscillator
根据铷原子频标的工作原理,其电路系统噪声是限制铷频标稳定度的关键因素之一,电路产生的交互调制噪声即晶振输出信号在调制频率(
上式中
与本实验室早期研究工作[9]中所设计的晶体振荡器相比,本文所设计低噪声晶体振荡器的设计电路采用2级放大电路,因此各级电路增益要求不需要很高,增加了电路的稳定性,同时也提高了隔离度.且关键频点的相噪特性得到进一步改善,在
4 结论
本文设计并实现了一款低噪声小型化10 MHz恒温晶体振荡器.振荡电路采用柯尔匹兹并联振荡电路,利用Leeson模型与ADS仿真指导设计,通过选用低噪声晶体管、提升回路品质因数、增大信号功率,实现了低相位噪声要求;通过直放式温控电路,将石英晶体温度控制在频率-温度拐点处,减小外部环境温度变化对晶体振荡器输出频率的影响.对该晶体振荡器的性能进行了测试和评估,测试结果表明,该晶体振荡器具有良好的短期频率稳定度(1.73×10−12/s)和优异的相位噪声性能(近端−102.7 dBc/Hz@1 Hz、远端−164.2 dBc/Hz@10 kHz),且其交调相噪对铷原子频标稳定度的贡献仅为2.3×10−13/
无
参考文献
High-performance laser-pumped rubidium frequency standard for satellite navigation
[J].DOI:10.1049/el.2011.0389 [本文引用: 1]
用于北斗三号卫星导航系统的星载铷原子钟特性
[J].
Characteristics of the space-borne rubidium atomic clocks for the BeiDou III navigation satellite system
[J].
A simple model of feedback oscillator noise spectrum
[J].DOI:10.1109/PROC.1966.4682 [本文引用: 1]
General theory of phase noise in electrical oscillators
[J].DOI:10.1109/4.658619 [本文引用: 1]
Phase noise in oscillators: a unifying theory and numerical methods for characterization
[J].DOI:10.1109/81.847872 [本文引用: 1]
A limit to the frequency stability of passive frequency standards due to an intermodulation effect
[J].DOI:10.1109/TIM.1990.1032896 [本文引用: 1]
小型化10 MHz恒温晶体振荡器设计
[J].DOI:10.3969/j.issn.1000-4556.2014.03.010 [本文引用: 1]
Design of a miniature 10 MHz oven crystal oscillator
[J].DOI:10.3969/j.issn.1000-4556.2014.03.010 [本文引用: 1]