图1
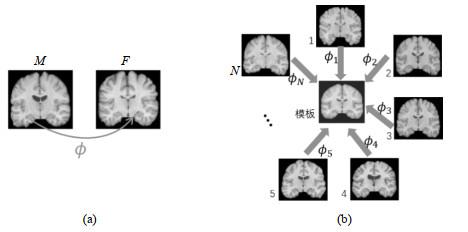
(a)成对配准(PW)和(b)群组配准(GW)图像配准示意图.(a)中M 代表浮动图像,F 为一组图像中任意一幅图像作为模板,φ 为变形场,(b)中模板由数据集中N 幅图像信息联合构建
Fig.1
Schematic diagrams of image registration for (a) PW and (b) GW. In Fig. (a), M represents a moving image, F represents any image in the group image as a template, and φ is the deformation field. In Fig. (b), the template is jointly constructed by N images in the data set
图2
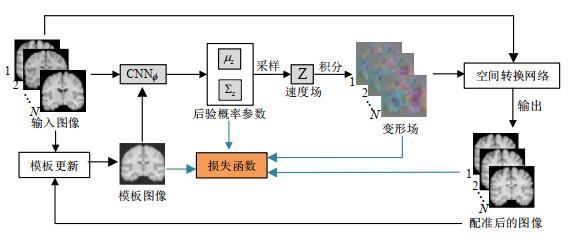
基于变分推断的磁共振图像群组配准框架
Fig.2
Overview of groupwise registration for magnetic resonance image based on variational inference
图3
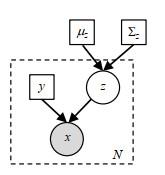
概率生成模型图解.白圈表示隐含变量,灰圈表示观测值(输入图像),方块表示参数.虚线矩形框表示里面的变量x 、y 、z 独立重复N 次.配准先验由高斯参数的均值μ z z
Fig.3
Probability generation model. White circle represents hidden variable, gray circle represents observed value (input image), and squares represent parameters. Dashed rectangle indicates the number of independent repeats N of the x , y , z variables inside. Registration prior is defined by the mean value μ z z
图4
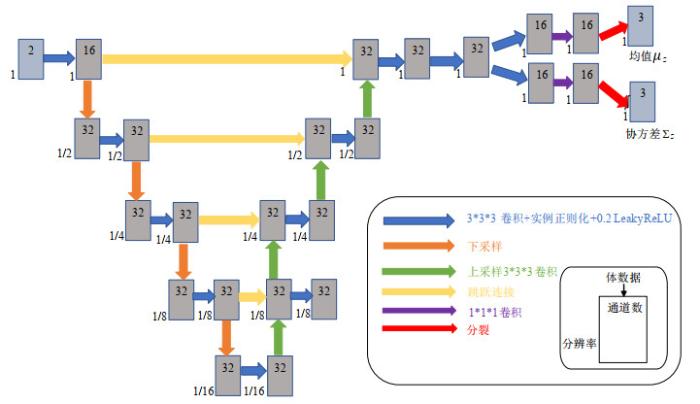
本文使用的CNN网络框架
Fig.4
CNN network frame in this research
图5
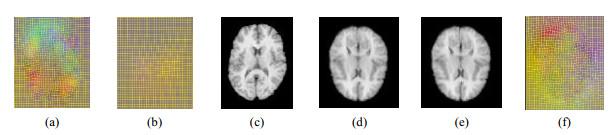
测试结果中心切片:(a)第一迭代的变形场;(b)第二次迭代的变形场;(c)浮动图像;(d)模板图像;(e)配准后的图像;(f)变形场
Fig.5
Central slice of test results: (a) Deformation field of the first iteration; (b) Deformation field of the second iteration; (c) Moving image; (d) Template image; (e) Image after registration; (f) Deformation field
图6
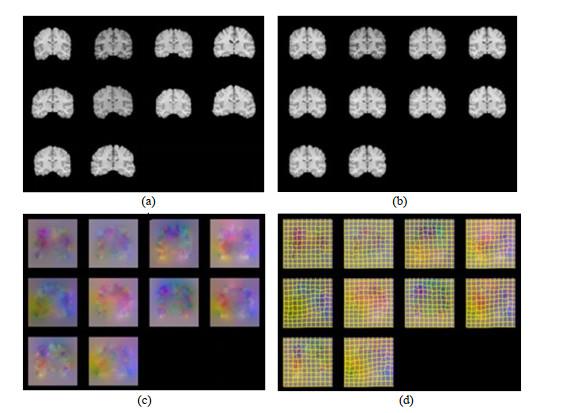
基于本文算法得到的10幅脑磁共振图像冠状位中心切片测试集群组配准结果.(a)原图像;(b)配准后的图像;(c)变形场的彩色图像;(d)变形场的网格图像
Fig.6
Results of groupwise registration of coronal section central slices of 10 brain magnetic resonance images by the proposed algorithms. (a) The original image; (b) The registered image (c) The color image of the deformation field; (d) The grid image of the deformation field
图7
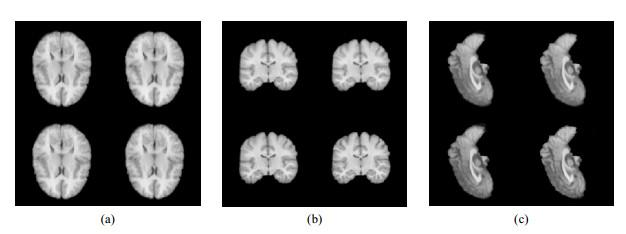
不同算法得到的扭曲图像的均值图像.(a)矢状位中心切片;(b)冠状位中心切片;(c)水平位中心切片.每幅小图中第一行从左到右依次为voxelmorph算法的均值图像,voxelmorph-diff算法的均值图像.第二行从左到右依次为Syn算法的均值图像和本文方法的均值图像
Fig.7
Mean images of distorted images by different algorithms. (a) Sagittal section central slice; (b) Coronal section central slice; (c) Horizontal section central slice. In each sub-figure, the first row from left to right is the mean image by voxelmorph algorithm, and voxelmorph-diff algorithm, the second row from left to right is the mean image by Syn algorithm and the method proposed in this work
图8
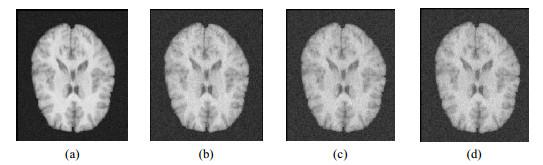
不同噪声强度的浮动图像:(a)~(d)噪声均值均为0,方差分别为0.001、0.002、0.003、0.004
Fig.8
Moving images with different noise intensities: (a)~(d) The mean values of noise are 0, and the variances are 0.001, 0.002, 0.003, and 0.004, respectively
图9
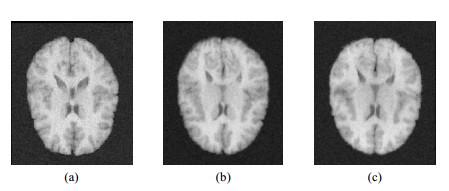
使用本文算法对含均值为0、方差为0.002的噪声图像进行配准的结果:(a)浮动的图像;(b)构建的模板;(c)配准后的图像
Fig.9
Groupwise registration result of LPBA 40 testing set with noise of mean value=0 and variance=0.002 using the proposed method: (a) Moving image; (b) Constructed template; (c) Image after registration
[1]
WANG Y, JIANG F, LIU Y Reference-free brain template construction with population symmetric registration
[J]. Med Biol Eng Comput, 2020 ,58 (9 ): 2083 - 2093 .
DOI:10.1007/s11517-020-02226-5
[本文引用: 3]
[2]
MARTÍN-GONZÁLEZ E, SEVILLA T, REVILLA-ORODEA A, et al Groupwise non-rigid registration with deep learning: an affordable solution applied to 2D cardiac cine MRI reconstruction
[J]. Entropy, 2020 ,22 (6 ): 687 .
DOI:10.3390/e22060687
[本文引用: 3]
[3]
GEE J C, REIVICH M, BILANIUK L, et al Evaluation of multiresolution elastic matching using mri data
[J]. Proc Spie, 1991 ,1445 ,226 - 234 .
DOI:10.1117/12.45220
[本文引用: 1]
[4]
RUECKERT D, SONODA L I Nonrigid registration using free-form deformations: application to breast mr images
[J]. IEEE T Med Imaging, 1999 ,18 (8 ): 712 - 721 .
DOI:10.1109/42.796284
[本文引用: 1]
[5]
THIRION J P Image matching as a diffusion process: an analogy with Maxwell's demons
[J]. Med Image Anal, 2011 ,2 (3 ): 243 - 260 .
[本文引用: 1]
[7]
ASAMI T, BOUIX S, WHITFORD T J, et al Longitudinal loss of gray matter volume in patients with first-episode schizophrenia: dartel automated analysis and roi validation
[J]. Neuroimage, 2012 ,59 (2 ): 986 - 996 .
DOI:10.1016/j.neuroimage.2011.08.066
[本文引用: 1]
[8]
GUIMOND A, MEUNIER J, THIRION J P Average brain models: a convergence study
[J]. Comput Vis Image Und, 2000 ,77 (2 ): 192 - 210 .
DOI:10.1006/cviu.1999.0815
[本文引用: 2]
[9]
SEGHERS D, D'AGOSTINO E, MAES F, et al. Construction of a brain template from mr images using state-of-the-art registration and segmentation techniques[C]// Medical Image Computing and Computer-Assisted Intervention--MICCAI 2004, 7th International Conference Saint-Malo, France, September 26-29, 2004, Proceedings, Part I. 2004.
[本文引用: 1]
[10]
WU G, JIA H, WANG Q, et al Sharpmean: groupwise registration guided by sharp mean image and tree-based registration
[J]. Neuroimage, 2011 ,56 (4 ): 1968 - 1981 .
DOI:10.1016/j.neuroimage.2011.03.050
[本文引用: 1]
[11]
WU G, WANG Q, JIA H, et al Feature-based groupwise registration by hierarchical anatomical correspondence detection
[J]. Hum Brain Mapp, 2012 ,33 (2 ): 253 - 271 .
DOI:10.1002/hbm.21209
[本文引用: 1]
[12]
YANOVSKY I, THOMPSON P M, OSHER S, et al. Topology preserving log-unbiased nonlinear image registration: theory and implementation[C]// IEEE Conference on Computer Vision & Pattern Recognition. Minneapolis, Minnesota, USA: IEEE, 2007.
[本文引用: 1]
[13]
WANG Q, CHEN L Y YAP P T, et al Groupwise registration based on hierarchical image clustering and atlas synthesis
[J]. Hum Brain Mapp, 2010 ,31 ,1128 - 1140 .
[本文引用: 1]
[14]
CHE T, ZHENG Y, CONG J, et al Deep group-wise registration for multi-spectural images from fundus images
[J]. IEEE Access, 2019 ,7 ,27650 - 27661 .
DOI:10.1109/ACCESS.2019.2901580
[本文引用: 2]
[15]
CHE T, ZHENG Y, SUI X, et al. Dgr-net: deep groupwise registration of multispectral images[C]// Information Processing in Medical Imaging - 26th International Conference , Hong Kong, china: IPMI, 2019: 706-717.
[本文引用: 2]
[16]
HAASE R, HELDMANN S, LELLMANN J. Deformable groupwise image registration using low-rank and sparse decomposition[EB/OL]. [2020-06-10].https://arxiv.org/abs/2001.03509.
[本文引用: 1]
[17]
DALCA A V, RAKIC M, GUTTAG J, et al. Learning conditional deformable templates with convolutional networks[C]//Neural Information Processing Systems 2019(NeurIPS 2019), Vancouver, BC, Canada, 2019: 804-816.
[本文引用: 2]
[18]
YU E M, DALCA A V, SABUNCU M R Learning conditional deformable shape templates for brain anatomy[M]. Lima : Machine Learning in Medical Imaging , 2020 , 353 - 352 .
[本文引用: 2]
[19]
SIEBERT H, HEINRICH M P Deep groupwise registration of mri using deforming autoencoders[M]. Berlin : Springer , 2020 , 236 - 241 .
[本文引用: 1]
[20]
HE Z Y, CHUNG A C S. Unsupervised end-to-end groupwise registration framework without generating templates[C]// 2020 IEEE International Conference on Image Processing (ICIP). IEEE, 2020: 375-379.
[本文引用: 2]
[21]
DALCA A V, BALAKRISHNAN G, GUTTAG J, et al Unsupervised learning of probabilistic diffeomorphic registration for images and surfaces
[J]. Med Image Anal, 2019 ,57 ,226 - 236 .
DOI:10.1016/j.media.2019.07.006
[本文引用: 2]
[22]
BALAKRISHNAN G, ZHAO A, SABUNCU M R, et al Voxelmorph: a learning framework for deformable medical image registration
[J]. IEEE T Med Imaging, 2019 ,1788 - 1800 .
[本文引用: 4]
[24]
王远军, 刘玉 基于图像集拓扑中心的群体配准方法
[J]. 波谱学杂志, 2018 ,35 (4 ): 60 - 67 .
URL
[本文引用: 1]
WANG Y J, LIU Y Group registration method based on topological center of images
[J]. Chinese J Magn Reson , 2018 ,35 (4 ): 60 - 67 .
URL
[本文引用: 1]
[25]
蔡文琴, 王远军 基于磁共振成像的人脑图谱构建方法研究进展
[J]. 波谱学杂志, 2020 ,37 (2 ): 241 - 253 .
URL
[本文引用: 1]
CAI W Q, WANG Y J Advances in the construction of the human brain map based on magnetic resonance imaging
[J]. Chinese J Magn Reson , 2020 ,37 (2 ): 241 - 253 .
URL
[本文引用: 1]
[26]
刘可文, 刘紫龙, 汪香玉, 等 基于级联卷积神经网络的前列腺磁共振图像分类
[J]. 波谱学杂志, 2020 ,37 (2 ): 152 - 161 .
URL
[本文引用: 1]
LIU K W, LIU Z L, WANG X Y, et al Prostate magnetic resonance image classification based on cascading convolutional neural networks
[J]. Chinese J Magn Reso , 2020 ,37 (2 ): 152 - 161 .
URL
[本文引用: 1]
Reference-free brain template construction with population symmetric registration
3
2020
... 各类脑成像中,磁共振成像(magnetic resonance imaging,MRI)由于可以显示血液和其状态的微小变化、无损伤定位大脑的功能活动,帮助病患发现早期脑部疾病,已经成为使用最广泛的脑功能研究手段,并为许多脑部疾病的检测与治疗带来福音.图像配准因具有信息匹配、信息融合的功能而成为在疾病分析中不可或缺的一部分.图像配准是MRI分析中的一项常见任务,也是许多领域中的一个活跃研究课题.它将图像空间对齐到一个共同的解剖空间[1 ] ,多幅图像的配准可以作为成对(pairwise,PW)配准或群组(groupwise,GW)配准问题来处理[2 ] .如下图1 所示,PW配准指定某一图像作为模板,其他图像与模板配准;GW配准中包括一个联合优化问题,用整个序列的信息创建模板,以避免在后续研究中引入偏差. ...
... 参考我们以前的工作[1 ,24 ,25 ] ,通过Dice、E{M_1} E{M_2}
... E{M_1} F 和总体之间的偏差[1 ] .N 为样本图像个数,D 为欧几里得距离测度.E{M_1} E{M_1}
Groupwise non-rigid registration with deep learning: an affordable solution applied to 2D cardiac cine MRI reconstruction
3
2020
... 各类脑成像中,磁共振成像(magnetic resonance imaging,MRI)由于可以显示血液和其状态的微小变化、无损伤定位大脑的功能活动,帮助病患发现早期脑部疾病,已经成为使用最广泛的脑功能研究手段,并为许多脑部疾病的检测与治疗带来福音.图像配准因具有信息匹配、信息融合的功能而成为在疾病分析中不可或缺的一部分.图像配准是MRI分析中的一项常见任务,也是许多领域中的一个活跃研究课题.它将图像空间对齐到一个共同的解剖空间[1 ] ,多幅图像的配准可以作为成对(pairwise,PW)配准或群组(groupwise,GW)配准问题来处理[2 ] .如下图1 所示,PW配准指定某一图像作为模板,其他图像与模板配准;GW配准中包括一个联合优化问题,用整个序列的信息创建模板,以避免在后续研究中引入偏差. ...
... 过去几十年,图像配准算法得到长足的发展.经典的配准算法和基于学习的方法受到很大关注,比较有代表性的算法有elastic模型[3 ] 、B样条[4 ] 和Demons[5 ] .几何变换的微分同胚性是当前配准领域非常看重的优点,比较有代表性的算法有LDDMM[6 ] 、DARTEL[7 ] 和Syn[2 ] .对于以上方法,大多数配准的模板都是任意指定的.但在图像集中随机选择的作为模板的图像往往不能代表图像集的结构变形和复杂性,并可能导致偏差和误导性分析,所以研究GW图像配准具有很重要的意义.近年来GW配准在配准领域越来越受欢迎,是因为它能提供更多有用的信息.Guimond等[8 ] 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
... GW配准的一个关键点是对组均值图像进行鲁棒和精确的估计.基于微分同胚[2 ] ,我们使用如下步骤构建模板. ...
Evaluation of multiresolution elastic matching using mri data
1
1991
... 过去几十年,图像配准算法得到长足的发展.经典的配准算法和基于学习的方法受到很大关注,比较有代表性的算法有elastic模型[3 ] 、B样条[4 ] 和Demons[5 ] .几何变换的微分同胚性是当前配准领域非常看重的优点,比较有代表性的算法有LDDMM[6 ] 、DARTEL[7 ] 和Syn[2 ] .对于以上方法,大多数配准的模板都是任意指定的.但在图像集中随机选择的作为模板的图像往往不能代表图像集的结构变形和复杂性,并可能导致偏差和误导性分析,所以研究GW图像配准具有很重要的意义.近年来GW配准在配准领域越来越受欢迎,是因为它能提供更多有用的信息.Guimond等[8 ] 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
Nonrigid registration using free-form deformations: application to breast mr images
1
1999
... 过去几十年,图像配准算法得到长足的发展.经典的配准算法和基于学习的方法受到很大关注,比较有代表性的算法有elastic模型[3 ] 、B样条[4 ] 和Demons[5 ] .几何变换的微分同胚性是当前配准领域非常看重的优点,比较有代表性的算法有LDDMM[6 ] 、DARTEL[7 ] 和Syn[2 ] .对于以上方法,大多数配准的模板都是任意指定的.但在图像集中随机选择的作为模板的图像往往不能代表图像集的结构变形和复杂性,并可能导致偏差和误导性分析,所以研究GW图像配准具有很重要的意义.近年来GW配准在配准领域越来越受欢迎,是因为它能提供更多有用的信息.Guimond等[8 ] 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
Image matching as a diffusion process: an analogy with Maxwell's demons
1
2011
... 过去几十年,图像配准算法得到长足的发展.经典的配准算法和基于学习的方法受到很大关注,比较有代表性的算法有elastic模型[3 ] 、B样条[4 ] 和Demons[5 ] .几何变换的微分同胚性是当前配准领域非常看重的优点,比较有代表性的算法有LDDMM[6 ] 、DARTEL[7 ] 和Syn[2 ] .对于以上方法,大多数配准的模板都是任意指定的.但在图像集中随机选择的作为模板的图像往往不能代表图像集的结构变形和复杂性,并可能导致偏差和误导性分析,所以研究GW图像配准具有很重要的意义.近年来GW配准在配准领域越来越受欢迎,是因为它能提供更多有用的信息.Guimond等[8 ] 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
Quantitative evaluation of lddmm, freesurfer, and caret for cortical surface mapping
1
2010
... 过去几十年,图像配准算法得到长足的发展.经典的配准算法和基于学习的方法受到很大关注,比较有代表性的算法有elastic模型[3 ] 、B样条[4 ] 和Demons[5 ] .几何变换的微分同胚性是当前配准领域非常看重的优点,比较有代表性的算法有LDDMM[6 ] 、DARTEL[7 ] 和Syn[2 ] .对于以上方法,大多数配准的模板都是任意指定的.但在图像集中随机选择的作为模板的图像往往不能代表图像集的结构变形和复杂性,并可能导致偏差和误导性分析,所以研究GW图像配准具有很重要的意义.近年来GW配准在配准领域越来越受欢迎,是因为它能提供更多有用的信息.Guimond等[8 ] 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
Longitudinal loss of gray matter volume in patients with first-episode schizophrenia: dartel automated analysis and roi validation
1
2012
... 过去几十年,图像配准算法得到长足的发展.经典的配准算法和基于学习的方法受到很大关注,比较有代表性的算法有elastic模型[3 ] 、B样条[4 ] 和Demons[5 ] .几何变换的微分同胚性是当前配准领域非常看重的优点,比较有代表性的算法有LDDMM[6 ] 、DARTEL[7 ] 和Syn[2 ] .对于以上方法,大多数配准的模板都是任意指定的.但在图像集中随机选择的作为模板的图像往往不能代表图像集的结构变形和复杂性,并可能导致偏差和误导性分析,所以研究GW图像配准具有很重要的意义.近年来GW配准在配准领域越来越受欢迎,是因为它能提供更多有用的信息.Guimond等[8 ] 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
Average brain models: a convergence study
2
2000
... 过去几十年,图像配准算法得到长足的发展.经典的配准算法和基于学习的方法受到很大关注,比较有代表性的算法有elastic模型[3 ] 、B样条[4 ] 和Demons[5 ] .几何变换的微分同胚性是当前配准领域非常看重的优点,比较有代表性的算法有LDDMM[6 ] 、DARTEL[7 ] 和Syn[2 ] .对于以上方法,大多数配准的模板都是任意指定的.但在图像集中随机选择的作为模板的图像往往不能代表图像集的结构变形和复杂性,并可能导致偏差和误导性分析,所以研究GW图像配准具有很重要的意义.近年来GW配准在配准领域越来越受欢迎,是因为它能提供更多有用的信息.Guimond等[8 ] 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
... 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
1
... 过去几十年,图像配准算法得到长足的发展.经典的配准算法和基于学习的方法受到很大关注,比较有代表性的算法有elastic模型[3 ] 、B样条[4 ] 和Demons[5 ] .几何变换的微分同胚性是当前配准领域非常看重的优点,比较有代表性的算法有LDDMM[6 ] 、DARTEL[7 ] 和Syn[2 ] .对于以上方法,大多数配准的模板都是任意指定的.但在图像集中随机选择的作为模板的图像往往不能代表图像集的结构变形和复杂性,并可能导致偏差和误导性分析,所以研究GW图像配准具有很重要的意义.近年来GW配准在配准领域越来越受欢迎,是因为它能提供更多有用的信息.Guimond等[8 ] 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
Sharpmean: groupwise registration guided by sharp mean image and tree-based registration
1
2011
... 过去几十年,图像配准算法得到长足的发展.经典的配准算法和基于学习的方法受到很大关注,比较有代表性的算法有elastic模型[3 ] 、B样条[4 ] 和Demons[5 ] .几何变换的微分同胚性是当前配准领域非常看重的优点,比较有代表性的算法有LDDMM[6 ] 、DARTEL[7 ] 和Syn[2 ] .对于以上方法,大多数配准的模板都是任意指定的.但在图像集中随机选择的作为模板的图像往往不能代表图像集的结构变形和复杂性,并可能导致偏差和误导性分析,所以研究GW图像配准具有很重要的意义.近年来GW配准在配准领域越来越受欢迎,是因为它能提供更多有用的信息.Guimond等[8 ] 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
Feature-based groupwise registration by hierarchical anatomical correspondence detection
1
2012
... 过去几十年,图像配准算法得到长足的发展.经典的配准算法和基于学习的方法受到很大关注,比较有代表性的算法有elastic模型[3 ] 、B样条[4 ] 和Demons[5 ] .几何变换的微分同胚性是当前配准领域非常看重的优点,比较有代表性的算法有LDDMM[6 ] 、DARTEL[7 ] 和Syn[2 ] .对于以上方法,大多数配准的模板都是任意指定的.但在图像集中随机选择的作为模板的图像往往不能代表图像集的结构变形和复杂性,并可能导致偏差和误导性分析,所以研究GW图像配准具有很重要的意义.近年来GW配准在配准领域越来越受欢迎,是因为它能提供更多有用的信息.Guimond等[8 ] 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
1
... 过去几十年,图像配准算法得到长足的发展.经典的配准算法和基于学习的方法受到很大关注,比较有代表性的算法有elastic模型[3 ] 、B样条[4 ] 和Demons[5 ] .几何变换的微分同胚性是当前配准领域非常看重的优点,比较有代表性的算法有LDDMM[6 ] 、DARTEL[7 ] 和Syn[2 ] .对于以上方法,大多数配准的模板都是任意指定的.但在图像集中随机选择的作为模板的图像往往不能代表图像集的结构变形和复杂性,并可能导致偏差和误导性分析,所以研究GW图像配准具有很重要的意义.近年来GW配准在配准领域越来越受欢迎,是因为它能提供更多有用的信息.Guimond等[8 ] 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
Groupwise registration based on hierarchical image clustering and atlas synthesis
1
2010
... 过去几十年,图像配准算法得到长足的发展.经典的配准算法和基于学习的方法受到很大关注,比较有代表性的算法有elastic模型[3 ] 、B样条[4 ] 和Demons[5 ] .几何变换的微分同胚性是当前配准领域非常看重的优点,比较有代表性的算法有LDDMM[6 ] 、DARTEL[7 ] 和Syn[2 ] .对于以上方法,大多数配准的模板都是任意指定的.但在图像集中随机选择的作为模板的图像往往不能代表图像集的结构变形和复杂性,并可能导致偏差和误导性分析,所以研究GW图像配准具有很重要的意义.近年来GW配准在配准领域越来越受欢迎,是因为它能提供更多有用的信息.Guimond等[8 ] 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
Deep group-wise registration for multi-spectural images from fundus images
2
2019
... 过去几十年,图像配准算法得到长足的发展.经典的配准算法和基于学习的方法受到很大关注,比较有代表性的算法有elastic模型[3 ] 、B样条[4 ] 和Demons[5 ] .几何变换的微分同胚性是当前配准领域非常看重的优点,比较有代表性的算法有LDDMM[6 ] 、DARTEL[7 ] 和Syn[2 ] .对于以上方法,大多数配准的模板都是任意指定的.但在图像集中随机选择的作为模板的图像往往不能代表图像集的结构变形和复杂性,并可能导致偏差和误导性分析,所以研究GW图像配准具有很重要的意义.近年来GW配准在配准领域越来越受欢迎,是因为它能提供更多有用的信息.Guimond等[8 ] 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
... 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
2
... 过去几十年,图像配准算法得到长足的发展.经典的配准算法和基于学习的方法受到很大关注,比较有代表性的算法有elastic模型[3 ] 、B样条[4 ] 和Demons[5 ] .几何变换的微分同胚性是当前配准领域非常看重的优点,比较有代表性的算法有LDDMM[6 ] 、DARTEL[7 ] 和Syn[2 ] .对于以上方法,大多数配准的模板都是任意指定的.但在图像集中随机选择的作为模板的图像往往不能代表图像集的结构变形和复杂性,并可能导致偏差和误导性分析,所以研究GW图像配准具有很重要的意义.近年来GW配准在配准领域越来越受欢迎,是因为它能提供更多有用的信息.Guimond等[8 ] 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
... ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
1
... 过去几十年,图像配准算法得到长足的发展.经典的配准算法和基于学习的方法受到很大关注,比较有代表性的算法有elastic模型[3 ] 、B样条[4 ] 和Demons[5 ] .几何变换的微分同胚性是当前配准领域非常看重的优点,比较有代表性的算法有LDDMM[6 ] 、DARTEL[7 ] 和Syn[2 ] .对于以上方法,大多数配准的模板都是任意指定的.但在图像集中随机选择的作为模板的图像往往不能代表图像集的结构变形和复杂性,并可能导致偏差和误导性分析,所以研究GW图像配准具有很重要的意义.近年来GW配准在配准领域越来越受欢迎,是因为它能提供更多有用的信息.Guimond等[8 ] 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
2
... 过去几十年,图像配准算法得到长足的发展.经典的配准算法和基于学习的方法受到很大关注,比较有代表性的算法有elastic模型[3 ] 、B样条[4 ] 和Demons[5 ] .几何变换的微分同胚性是当前配准领域非常看重的优点,比较有代表性的算法有LDDMM[6 ] 、DARTEL[7 ] 和Syn[2 ] .对于以上方法,大多数配准的模板都是任意指定的.但在图像集中随机选择的作为模板的图像往往不能代表图像集的结构变形和复杂性,并可能导致偏差和误导性分析,所以研究GW图像配准具有很重要的意义.近年来GW配准在配准领域越来越受欢迎,是因为它能提供更多有用的信息.Guimond等[8 ] 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
... 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
2
2020
... 过去几十年,图像配准算法得到长足的发展.经典的配准算法和基于学习的方法受到很大关注,比较有代表性的算法有elastic模型[3 ] 、B样条[4 ] 和Demons[5 ] .几何变换的微分同胚性是当前配准领域非常看重的优点,比较有代表性的算法有LDDMM[6 ] 、DARTEL[7 ] 和Syn[2 ] .对于以上方法,大多数配准的模板都是任意指定的.但在图像集中随机选择的作为模板的图像往往不能代表图像集的结构变形和复杂性,并可能导致偏差和误导性分析,所以研究GW图像配准具有很重要的意义.近年来GW配准在配准领域越来越受欢迎,是因为它能提供更多有用的信息.Guimond等[8 ] 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
... ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
1
2020
... 过去几十年,图像配准算法得到长足的发展.经典的配准算法和基于学习的方法受到很大关注,比较有代表性的算法有elastic模型[3 ] 、B样条[4 ] 和Demons[5 ] .几何变换的微分同胚性是当前配准领域非常看重的优点,比较有代表性的算法有LDDMM[6 ] 、DARTEL[7 ] 和Syn[2 ] .对于以上方法,大多数配准的模板都是任意指定的.但在图像集中随机选择的作为模板的图像往往不能代表图像集的结构变形和复杂性,并可能导致偏差和误导性分析,所以研究GW图像配准具有很重要的意义.近年来GW配准在配准领域越来越受欢迎,是因为它能提供更多有用的信息.Guimond等[8 ] 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
2
... 过去几十年,图像配准算法得到长足的发展.经典的配准算法和基于学习的方法受到很大关注,比较有代表性的算法有elastic模型[3 ] 、B样条[4 ] 和Demons[5 ] .几何变换的微分同胚性是当前配准领域非常看重的优点,比较有代表性的算法有LDDMM[6 ] 、DARTEL[7 ] 和Syn[2 ] .对于以上方法,大多数配准的模板都是任意指定的.但在图像集中随机选择的作为模板的图像往往不能代表图像集的结构变形和复杂性,并可能导致偏差和误导性分析,所以研究GW图像配准具有很重要的意义.近年来GW配准在配准领域越来越受欢迎,是因为它能提供更多有用的信息.Guimond等[8 ] 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
... 其中\Omega f,g:\Omega \to R \Omega \subset {R^3} \bar f(x) = \sum\nolimits_{{x_i}} {f({x_i})/{n^3}} \hat f(x){\text{ = }}\sum\nolimits_{{x_i}} {[f({x_i}) - \bar f} (x){]^2} {x_i} x {n^3} 20 ],这里我们使用n = 5 x
Unsupervised learning of probabilistic diffeomorphic registration for images and surfaces
2
2019
... 过去几十年,图像配准算法得到长足的发展.经典的配准算法和基于学习的方法受到很大关注,比较有代表性的算法有elastic模型[3 ] 、B样条[4 ] 和Demons[5 ] .几何变换的微分同胚性是当前配准领域非常看重的优点,比较有代表性的算法有LDDMM[6 ] 、DARTEL[7 ] 和Syn[2 ] .对于以上方法,大多数配准的模板都是任意指定的.但在图像集中随机选择的作为模板的图像往往不能代表图像集的结构变形和复杂性,并可能导致偏差和误导性分析,所以研究GW图像配准具有很重要的意义.近年来GW配准在配准领域越来越受欢迎,是因为它能提供更多有用的信息.Guimond等[8 ] 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
... 定义公共空间先验的一种方法是对输入图像的潜在变量z 进行高斯建模[21 ] ,所得概率图谱用作参考.为避免选择固定模板图像带来的偏差并考虑总体信息,对输入图像的潜在变量进行高斯建模,则 p(z)
Voxelmorph: a learning framework for deformable medical image registration
4
2019
... 过去几十年,图像配准算法得到长足的发展.经典的配准算法和基于学习的方法受到很大关注,比较有代表性的算法有elastic模型[3 ] 、B样条[4 ] 和Demons[5 ] .几何变换的微分同胚性是当前配准领域非常看重的优点,比较有代表性的算法有LDDMM[6 ] 、DARTEL[7 ] 和Syn[2 ] .对于以上方法,大多数配准的模板都是任意指定的.但在图像集中随机选择的作为模板的图像往往不能代表图像集的结构变形和复杂性,并可能导致偏差和误导性分析,所以研究GW图像配准具有很重要的意义.近年来GW配准在配准领域越来越受欢迎,是因为它能提供更多有用的信息.Guimond等[8 ] 提出一种建立平均解剖模型的方法,该方法在单个图像(模板图像)中提供平均强度和平均形状,以平均的方式消除了脑形状和强度变化.类似于文献[8 ]的方法,Seghers等[9 ] 通过选择每个图像作为模板来对齐所有图像,并且使图像与平均变形场非刚性对齐.Wu等[10 ] 提出使用自适应加权策略的SharpMean配准方法,进一步构建基于特征的GW配准方法,该方法在配准过程中实现解剖学上合理的对应.以上提出的几种GW配准算法都是将图像配准到它们的相似图像,其中相似图像称为中间模板[11 ,12 ] . Wang等[13 ] 提出一种类似金字塔式的配准框架,该框架可以有效地配准大的图像数据集,配准性能相对较好.随着深度学习技术的兴起,许多研究者也在探索深度神经网络在GW图像配准中的应用.Che等[14 ,15 ] 提出一个由主成分分析构建的模板图像引导的无偏差的深度GW配准框架,适用于多光谱图像.类似于文献[14 ,15 ]的方法,Haase等[16 ] 使用了鲁棒的主成成分分析方法.不同的是,在变分正则化的基础上,他们提出基于一阶原始对偶优化的多级方案来解决由此产生的非参数配准的问题.由于单个模板可能无法捕捉数据集的可变形,Dalca等[17 ,18 ] 提出一种用于产生条件模板的配准框架和学习策略.类似于文献[17 ,18 ]使用可变模板的范例做法,Siebert等[19 ] 提出使用自动编码器实现GW配准的方法,以无监督学习方式学习图像的形状和外观.遵循可变形模板的范例,将其应用到图像集上对齐.最近,He等[20 ] 提出一种无监督的端到端GW框架,该框架具有多步机制来逐步优化输出的变形场,而无需模板.这项工作主要用于二维医学图像配准任务,且预估的变形场不是微分同胚域.Balakrishnan等[21 ] 提出一种基于卷积神经网络(convolutional neural networks,CNN)的无监督PW配准方法,他们使用了一种类似于U-Net的架构,并将其命名为voxelmorph.后来,他们扩展了该方法,提出一个基于无监督学习的推理算法,并将其命名为voxelmorph-diff[22 ] .实验结果表明,他们提出的算法有助于提高Dice系数,性能与ANT和NifTYG相当,但是计算效率是ANT的150倍,是NifTYG的40倍.voxelmorph-diff和voxelmorph是近年来基于深度学习的PW配准领域比较经典的方法,计算效率也高于现有的一般方法. ...
... 根据文献[22 ],对于每一个样本可知: ...
... GW方法旨在找到GW图像到模板空间的最佳变换,以及模板图像的计算.本文的网络架构包括解码网络、CNN、空间转换器和损失函数.在文献[22 ]中,Balakrishnan等明确的选择模板图像和运动图像来进行PW配准.相比之下,在我们的方法中,在输入到CNN网络之前,先将输入图像和生成的模板图像在通道堆叠并送入CNN网络,学习群组图像到模板图像的公共空间变换. ...
... 本文还选取配准精度较高的Syn、voxelmorph-diff和voxelmorph三种算法进行了对比,其中后面两种方法是基于深度学习的经典的可变形PW配准算法.Syn使用ANTsPy实现,使用互相关(cross correlation,CC)系数作为其度量标准.voxelmorph-diff和voxelmorph两种方法使用与文献[22 ]相同的网络参数进行训练. ...
Construction of a 3d probabilistic atlas of human cortical structures.
1
2008
... 为验证本文提出算法的性能,使用公开数据集LONI LPBA40[23 ] 进行实验.对数据集的所有3D磁共振图像都使用FSL和FreeSurfer软件进行偏移场矫正、大脑提取及线性配准、体素重采样至 1 mm* 1 mm* 1 mm和尺寸裁剪为160* 160* 192等预处理.并将含有40个3D磁共振图像的LPBA40数据集划分为训练集(30)、测试集(10).每个3D图像均有对应的标签(54个脑区标记),这些标签可用于评价配准的精度. ...
基于图像集拓扑中心的群体配准方法
1
2018
... 参考我们以前的工作[1 ,24 ,25 ] ,通过Dice、E{M_1} E{M_2}
基于图像集拓扑中心的群体配准方法
1
2018
... 参考我们以前的工作[1 ,24 ,25 ] ,通过Dice、E{M_1} E{M_2}
基于磁共振成像的人脑图谱构建方法研究进展
1
2020
... 参考我们以前的工作[1 ,24 ,25 ] ,通过Dice、E{M_1} E{M_2}
基于磁共振成像的人脑图谱构建方法研究进展
1
2020
... 参考我们以前的工作[1 ,24 ,25 ] ,通过Dice、E{M_1} E{M_2}
基于级联卷积神经网络的前列腺磁共振图像分类
1
2020
... 由于训练集数据较少,我们在不发生图像形变的前提下,使用左右翻转和上下翻转的方式进行数据扩增[26 ] ,以大大增强模型的泛化能力,减少模型过拟合的情况.算法在Tensorflow框架中实现,使用学习率为1e-5的Adam优化器优化训练,迭代次数为15 000次.超参数 {\lambda _a} {\lambda _b} 图5 所示.因为第2次配准域接近正交网格,停止迭代,并将其作为测试的模板图像. ...
基于级联卷积神经网络的前列腺磁共振图像分类
1
2020
... 由于训练集数据较少,我们在不发生图像形变的前提下,使用左右翻转和上下翻转的方式进行数据扩增[26 ] ,以大大增强模型的泛化能力,减少模型过拟合的情况.算法在Tensorflow框架中实现,使用学习率为1e-5的Adam优化器优化训练,迭代次数为15 000次.超参数 {\lambda _a} {\lambda _b} 图5 所示.因为第2次配准域接近正交网格,停止迭代,并将其作为测试的模板图像. ...