散弹噪声极限稳定度优于1×10-13 τ -1/2 的铷频标物理系统
聂帅 1 , 2 , 3 , 王鹏飞 , 1 , 2 , 赵峰 1 , 2 , 王芳 1 , 2 , 明刚 1 , 2 , 邱紫敬 1 , 2 , 康松柏 1 , 2 , 梅刚华 , 1 , 2
1. 中国科学院精密测量科学与技术创新研究院, 湖北 武汉 430071
2. 中国科学院原子频标重点实验室, 湖北 武汉 430071
3. 中国科学院大学, 北京 100049
A Physics Package with Shot-noise Limited Frequency Stability Better Than 1×10-13 τ -1/2 for Rubidium Atomic Frequency Standards
NIE Shuai 1 , 2 , 3 , WANG Peng-fei , 1 , 2 , ZHAO Feng 1 , 2 , WANG Fang 1 , 2 , MING Gang 1 , 2 , QIU Zi-jing 1 , 2 , KANG Song-bai 1 , 2 , MEI Gang-hua , 1 , 2
1. Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences, Wuhan 430071, China
2. Key Laboratory of Atomic Frequency Standards, Chinese Academy of Sciences, Wuhan 430071, China
3. University of Chinese Academy of Sciences, Beijing 100049, China
通讯作者: 王鹏飞, Tel: 15377057079, E-mail:wpengfei@apm.ac.cn 梅刚华, Tel: 027-87197190, E-mail:mei@apm.ac.cn
收稿日期: 2021-03-18
基金资助:
中国科学院重点部署项目 . ZDRW-KT-2021-2 国家自然科学基金青年科学基金资助项目 . 11903069
摘要
近年来,铷原子频标研究取得长足进展,频率稳定度达到10-13 τ -1/2 量级.为进一步改善铷频标稳定度性能,本文设计了一种高信噪比物理系统.物理系统中的腔泡组件采用微波场磁力线与量子化轴方向高度平行的开槽管式微波腔,滤光泡和吸收泡独立控温.抽运光源采用了光学滤光和同位素滤光双重滤光方案.本文实测了背景光电流I 0 和鉴频斜率Kd ,结果分别为95 μA和7.7 nA/Hz,在此基础上计算物理系统的散弹噪声极限稳定度为7.5×10-14 τ -1/2 .研究结果表明,只要锁频环路的电子学噪声得到有效控制,铷频标的频率稳定度突破1×10-13 τ -1/2 ,进入10-14 τ -1/2 量级是完全可能的.
关键词:
铷原子频标 物理系统 开槽管微波腔 散弹噪声 频率稳定度
Abstract
The performance of the rubidium (Rb) atomic frequency standard has achieved significant improvement in recent years. Its frequency stability has already reached the order of 10-13 τ -1/2 . To further improve Rb frequency standard's stability performance, we developed a high signal-to-noise ratio (SNR) physics package whose cavity-cell assembly consists of a slotted-tube microwave cavity, separated filter and absorption cells. The microwave cavity has a homogenous field distribution along the quantization axis, and the filter and absorption cells are temperature-controlled independently. We also used an optical and isotopic filtering scheme to suppress shot noise from the pumping light. The physics package's final background photocurrent I 0 and the frequency discrimination slope Kd were measured to be 95 μA and 7.7 nA/Hz, respectively, and the calculated limit stability of the shot noise of the physical package was 7.5×10-14 τ -1/2 . The result shows that Rb frequency standard can reach an unprecedented stability level below 1×10-13 τ -1/2 as long as the electronic system's noise could be well controlled.
Keywords:
rubidium atomic frequency standards physics package slotted-tube cavity shot noise frequency stability
本文引用格式
聂帅, 王鹏飞, 赵峰, 王芳, 明刚, 邱紫敬, 康松柏, 梅刚华. 散弹噪声极限稳定度优于1×10-13 τ -1/2 的铷频标物理系统 . 波谱学杂志 [J], 2022, 39(1): 108-114 doi:10.11938/cjmr20212897
NIE Shuai. A Physics Package with Shot-noise Limited Frequency Stability Better Than 1×10-13 τ -1/2 for Rubidium Atomic Frequency Standards . Chinese Journal of Magnetic Resonance
引言
近几十年来,卫星导航的应用极大促进了铷原子频标(简称铷频标)的发展.早期的铷频标频率稳定度指标在10−11 τ −1/2 水平.1990年代,Riley等[1 ] 为GPS IIR研制星载铷频标,短期稳定度为3×10−12 τ −1/2 .2010年,Dupuis等[2 ] 报道的为GPS IIF系统研制的星载铷频标,短期稳定度提升到1×10−12 τ −1/2 .目前GPS Ⅲ系统的星载铷频标短期稳定度为1×10−12 τ −1/2 [3 ] .Spectratime公司为Galileo系统研制的星载铷频标,短期稳定度为3×10−12 τ −1/2 [4 ] .本实验室长期致力于北斗卫星导航系统星载铷频标研制,用于北斗二号系统的星载铷频标,短期稳定度为3×10−12 τ −1/2 [5 ] ;用于北斗三号系统的星载铷频标,短期稳定度达到6.1×10−13 τ −1/2 [6 ] .本实验室郝强等[7 ] 设计出一种铷频标桌面系统,获得了2.4×10−13 τ −1/2 (1~100 s)稳定度测试结果.2018年,我们实现了一种铷频标整机,频率稳定度测定为2.1×10−13 τ −1/2 (1~100 s)[8 ] ,与郝强等的结果相当.这些结果表明传统铷频标性能已经逼近新一代激光抽运铷频标,目前已被报道的激光抽运铷频标的最好稳定度指标为1.4×10−13 τ −1/2 (1~100 s)[9 ] .铷频标的频率稳定度能否进一步提升,达到甚至超过激光抽运铷频标的水平,是一个很值得研究的问题.
铷频标的频率稳定度主要决定于物理系统产生的原子鉴频信号的信噪比和锁频环路的电子学噪声,主要难点是前者.最近,我们在文献[8 ] 工作的基础上,设计了一种新结构物理系统,实测了原子鉴频信号的信噪比和鉴频斜率,据此计算出物理系统散弹噪声极限稳定度为7.5×10−14 τ −1/2 .该结果表明,从物理系统设计角度看,铷频标频率稳定度突破1×10−13 τ −1/2 是完全可能的.
1 铷频标散弹噪声极限稳定度
频率稳定度是铷原子频标的核心指标.铷频标的频率稳定度可以分为短期稳定度和长期稳定度两类.短期稳定度好并不直接导致长期稳定度好,但是决定铷频标稳定度极限的是短期稳定度.铷频标整机由物理系统和电路系统两部分构成,整机的短期稳定度主要受限于物理系统的散弹噪声极限稳定度和电路系统交互调制效应,本文重点研究前一个因素.
其中,S i K d v 0 τ 为采样时间,e 为电子电荷量.S i I 0 K d
铷原子频标是基于光-微波双共振原理设计的.铷光谱灯灯泡中87 Rb原子发出的光,经过滤光后,对位于微波腔内的吸收泡中87 Rb原子进行光抽运,实现87 Rb原子钟跃迁两个能级(F = 2 m F = 0 F = 1 m F = 0 87 Rb原子发生相互作用.当微波频率与钟跃迁频率相近时,原子从(F = 2 m F = 0 F = 1 m F = 0 I 0 ΔI 决定鉴频斜率K d
由以上分析可知,改善铷频标的稳定度,可从两方面入手.一是降低散弹噪声,主要途径是提高光抽运效率,以强度最低的抽运光获取最大的钟跃迁能级布居数反转.二是增强原子的微波跃迁信号,主要途径是优化微波腔的特性,增加参与跃迁的原子数量.这构成本项研究的主要思路.
2 物理系统的结构和设计
2.1 物理系统的结构
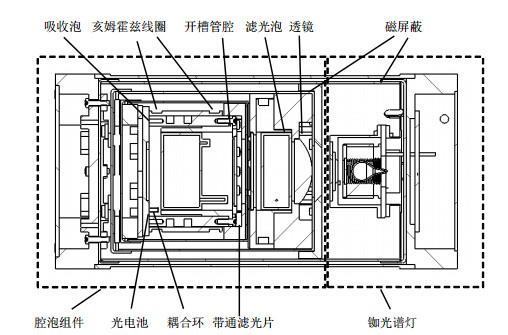
物理系统的结构示于图 1 .铷光谱灯发出的光经透镜准直后进入滤光泡进行同位素滤光,再通过带通式干涉滤光片进行光学滤光.滤光后的光束进入铷吸收泡,对其中的87 Rb原子进行光抽运.外部微波信号经耦合环馈入微波腔,激励吸收泡中的87 Rb原子发生微波跃迁,光吸收信号用光电池探测.亥姆霍兹线圈产生弱定向磁场,为原子的微波跃迁提供量子化轴.磁屏蔽的作用是消除外部地磁场和杂散磁场对原子跃迁信号的干扰.
图1
图1
分区控温的物理系统的结构
Fig.1
Physics package whose filter and absorption cells are temperature-controlled independently
2.2 抽运光滤光和光路优化
为降低散弹噪声,本文采用了光学滤光和同位素滤光两级滤光方案.光学滤光的作用是滤除光谱灯中启辉气体(本实验中为Xe气)发光.这种光谱成分对铷原子光抽运没有贡献,仅贡献为散弹噪声.同位素滤光的作用是滤除光谱灯铷发光光谱中的无用成分,这部分光也仅贡献为散弹噪声.为了提高同位素滤光效率,采用了吸收泡和滤光泡分别独立温控的设计方案.在我们先前的设计中,吸收泡和滤光泡均在微波腔内,共用一个温度控制器[8 ] .这种设计的优点是系统的集成度较高,缺点是滤光泡温度不能独立调节,这会导致同位素滤光不完全,抽运光中仍含有较多无用光成分,形成散弹噪声[11 ] .
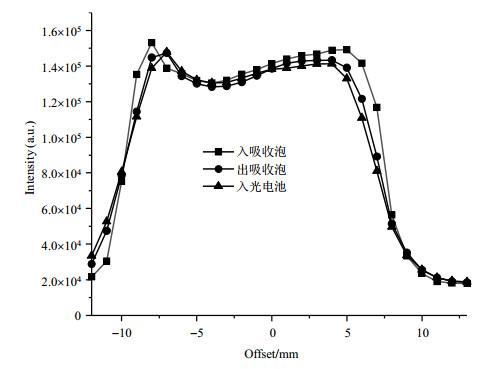
为了使更多的原子参与双共振跃迁,提高原子的利用率,需要对光束进行准直,使其变为准平行光,且光束尽可能充满整个吸收泡.光束准直不能简单采用长焦距透镜,焦距过长会导致光的利用率过低,影响抽运效果.焦距过短,则光束准直更加困难.为了兼顾这一矛盾,我们选用了直径为25 mm、焦距为25.8 mm的透镜.考虑到灯泡的体光源特性,灯泡不能严格放置在透镜焦点位置,而应根据光束的准直效果优化选取.图 2 给出了灯泡与透镜之间的距离优化以后光路各处光斑等效直径(用光强半高宽定义)测量结果.由图 2 可见,在吸收泡入光面、出光面和光电池处(参见图 1 ),光斑等效直径基本不变,约为20 mm,略小于吸收泡内径27 mm.吸收泡内靠近泡壁处的铷原子由于壁弛豫效应存在较大的谱线增宽[12 ] ,不是理想的工作物质,因此光斑直径略小于吸收泡内径的设计是合理的.
图2
图2
光路准直后光在吸收泡入光面、吸收泡出光面、光电池位置处的光强分布
Fig.2
Light intensity distribution in the incident surface of absorption cell, the exit surface of absorption cell, and photovoltaic battery
2.3 微波腔设计
微波腔采用本实验室发明的开槽管式微波腔[13 ] ,腔内径为30 mm,可以容纳外径为30 mm的吸收泡.微波腔内驻波场的特性直接影响钟跃迁信号强度.根据量子力学原理,只有平行于量子化轴(一般为腔轴)的微波场磁分量,才能够激励铷原子的钟跃迁.因此,微波腔特性用反映微波腔内钟跃迁频率处的驻波场磁场分量与量子化轴平行程度的方向因子ξ 表征,它定义为在腔内微波与原子作用区中,沿量子化轴方向的磁场能量与总磁场能量之比[14 ] :
其中V 为作用区体积,| H z | 2 | H | 2 ξ 取值范围为0~1,ξ 数值越趋近于1,则微波磁场与量子化轴平行度越高.
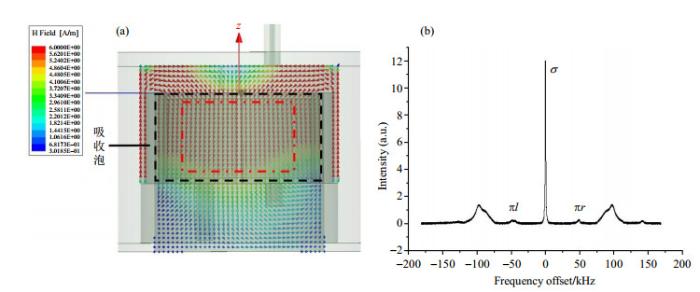
微波腔内的微波场分布和方向因子可以借助有限元软件HFSS仿真计算得到,方向因子还可以通过测量的87 Rb原子基态5S1/2 超精细Zeeman子能级跃迁谱获得[14 ] .磁场分布示于图 3(a) ,可以看出,腔内磁场能量集中于吸收泡所处区域,且磁场高度平行于量子化轴,计算了图 3(a) 中红色虚线区域内的方向因子为0.94.图 3(b) 为实验测量得到的87 Rb原子Zeeman子能级跃迁谱.可以看出全部7条跃迁谱线中,微波场平行分量激励的σ 跃迁谱线强度远大于垂直分量激励的π跃迁谱线强度,表明微波场中平行于量子化轴的部分为主要成分.设谱中心的σ 跃迁(即钟跃迁)谱线强度为I σ I π r I π l ξ = I σ / ( I σ + I π r + I π l ) . 由此得到方向因子ξ 的实测值为0.87, 与仿真结果一致.高ξ 值微波腔的应用对于增强87 Rb原子的钟跃迁信号是有利的.
图3
图3
(a) 开槽管腔内磁场分布;(b) 87 Rb原子基态能级Zeeman谱
Fig.3
(a) Magnetic field distribution in slotted-tube cavity; (b) Zeeman spectrum of 87 Rb ground state
3 散弹噪声极限稳定度的评估
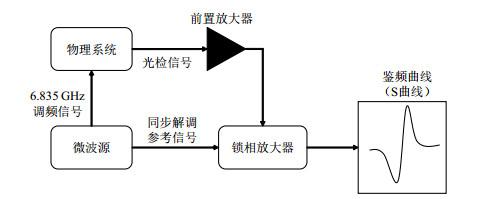
物理系统散弹噪声极限稳定度可以在开环情况下独立评估.由(1)式和(2)式可知,只要测量鉴频斜率K d I 0 I 0 K d 图 4 所示实验装置进行测量.在该装置中,微波源产生两路信号:一路为中心频率为钟跃迁频率6.835 GHz的调频微波信号(调制频率136 Hz);另一路为136 Hz同步解调参考信号.调频微波信号馈入到物理系统,激励87 Rb原子跃迁,光电池产生交流光检信号.光检信号经前置放大器放大后进入锁相放大器,对信号进行同步解调.锁相放大器输出电流除以前置放大器的交流放大倍数,即为物理系统的鉴频信号电流.当调频微波信号在钟跃迁频率附近处扫频时,同时记录鉴频信号和扫描频差,即得到“S”状鉴频曲线.鉴频曲线中心部分的斜率,即为鉴频斜率K d .
图4
图4
测量鉴频曲线的原理
Fig.4
Functional block diagram of discrimination curve measurement
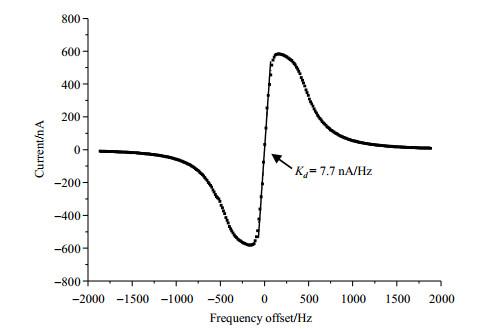
本文优化了物理系统的工作参数,发现当吸收泡温度为64 ℃、滤光泡温度为85 ℃时,鉴频斜率最大.此时,测得背景光电流I 0 图 5 .由图 5 的曲线,计算鉴频斜率K d I 0 K d −14 τ −1/2 .
图5
图5
鉴频曲线测量结果
Fig.5
Measured discrimination curve of the physics package
4 结论
本文设计了一种高信噪比的铷原子频标物理系统.物理系统中的腔泡组件采用方向因子为0.87的开槽管式微波腔,滤光泡和吸收泡直径为30 mm,采用分区控温方案,工作温度分别为64 ℃和85 ℃.抽运光源为充有Xe气的铷光谱灯,采用光学滤光和同位素滤光双重滤光方案进行滤光.实测了背景光电流I 0 K d −14 τ −1/2 .近年来铷原子频标研究取得长足进展,频率稳定度已达到10−13 τ −1/2 量级.本文的结果表明,物理系统的散弹噪声可以降低到1×10−13 τ −1/2 以下,只要锁频环路的电子学噪声得到有效控制,铷频标的频率稳定度突破1×10−13 τ −1/2 ,进入10−14 τ −1/2 量级是完全可能的.
参考文献
View Option
[1]
RILEY J W. Rubidium atomic frequency standards for GPS block ⅡR[C]//Proceedings of 22nd Annual Precise Time and Time Interval (PTTI) Applications and Planning Meeting. Vienna, Virginia, 1990: 221-230.
[本文引用: 1]
[2]
DUPUIS R T, LYNCH T J, VACCARO J R, et al. Rubidium frequency standard for the GPS ⅡF program and modifications for the RAFSMOD program[C]//Proceedings of the 23rd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2010). 2010: 781-788
[本文引用: 1]
[3]
RILEY J W. A history of the rubidium frequency standard[OL]. http://ieee-uffc.org/about-us/history/a-history-of-the-rubidium-frequency-standard.pdf. 2019.
[本文引用: 1]
[4]
iSpace+ Space Qualified RAFS Spec[R]. https://www.orolia.com/sites/default/files/document-files/Spectratime-RAFS-Spec-01-19-21.pdf. 2021.
[本文引用: 1]
[5]
MEI G H, ZHONG D, AN S F, et al. Main features of space rubidium atomic frequency standard for BeiDou satellites[C]//2016 European Frequency and Time Forum (EFTF). IEEE, 2016: 1-4.
[本文引用: 1]
[6]
MEI G H , ZHAO F , Qi F , et al . Characteristics of the space-borne rubidium atomic clocks for the BeiDou Ⅲ navigation satellite system
[J]. Scientia Sinica: Physica, Mechanica & Astronomica , 2021 , 51 (1 ): 118 - 124 .
URL
[本文引用: 1]
梅刚华 , 赵峰 , 祁峰 , 等 . 用于北斗三号卫星导航系统的星载铷原子钟特性
[J]. 中国科学: 物理学力学天文学, 2021 , 51 (1 ): 118 - 124 .
URL
[本文引用: 1]
[7]
HAO Q , LI W B , HE S G , et al . A physics package for rubidium atomic frequency standard with a short-term stability of 2.4×10- 13 τ-1/2
[J]. Rev Sci Instrum, 2016 , 87 (12 ): 123111 .
DOI:10.1063/1.4972567
[本文引用: 1]
[8]
NIE S, WANG P F, QIU Z J, et al. A lamp-pumped rubidium atomic frequency standard with a short-term stability at the level of 2×10-13 τ-1/2 [C]//China Satellite Navigation Conference (CSNC) 2019 proceedings. Springer, Singapore, 2019: 556-563.
[本文引用: 3]
[9]
BANDI T , AFFOLDERBACH C , STEFANUCCI C . et al, Compact high-performance continuous-wave double-resonance rubidium standard with 1.4×10-13 τ-1/2 stability
[J]. IEEE transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2014 , 61 (11 ): 1769 - 1778 .
DOI:10.1109/TUFFC.2013.005955
[本文引用: 1]
[10]
VANIER J . On the signal-to-noise ratio and short-term stability of passive rubidium frequency standards
[J]. IEEE T Instrum Meas, 1981 , 30 (4 ): 277 - 282 .
[本文引用: 1]
[11]
XU F , HAO Q , WANG P F , et al . A high signal to noise ratio physics package with a slotted-tube cavity for rubidium atomic clock
[J]. Acta Metrologica Sinica , 2016 , 37 (4 ): 437 - 440 .
[本文引用: 1]
许风 , 郝强 , 王鹏飞 , 等 . 基于开槽管腔的高信噪比铷原子钟物理系统
[J]. 计量学报, 2016 , 37 (4 ): 437 - 440 .
[本文引用: 1]
[12]
MICALIZIO S , GODONE A , LEVI F , et al . Pulsed optically pumped 87 Rb vapor cell frequency standard: A multilevel approach
[J]. Phys Rev A, 2009 , 79 (1 ): 013403 .
DOI:10.1103/PhysRevA.79.013403
[本文引用: 1]
[13]
MEI G H, ZHONG D, AN S F, et al. Miniaturized microwave cavity for atomic frequency standard: U.S. Patent, 6, 225, 870[P], 2001-05-01.
[本文引用: 1]
[14]
STEFANUCCI C , BANDI T , MERLI F , et al . Compact microwave cavity for high performance rubidium frequency standards
[J]. Rev Sci Instrum, 2012 , 83 , 104706 .
DOI:10.1063/1.4759023
[本文引用: 2]
1
... 近几十年来,卫星导航的应用极大促进了铷原子频标(简称铷频标)的发展.早期的铷频标频率稳定度指标在10−11 τ −1/2 水平.1990年代,Riley等[1 ] 为GPS IIR研制星载铷频标,短期稳定度为3×10−12 τ −1/2 .2010年,Dupuis等[2 ] 报道的为GPS IIF系统研制的星载铷频标,短期稳定度提升到1×10−12 τ −1/2 .目前GPS Ⅲ系统的星载铷频标短期稳定度为1×10−12 τ −1/2 [3 ] .Spectratime公司为Galileo系统研制的星载铷频标,短期稳定度为3×10−12 τ −1/2 [4 ] .本实验室长期致力于北斗卫星导航系统星载铷频标研制,用于北斗二号系统的星载铷频标,短期稳定度为3×10−12 τ −1/2 [5 ] ;用于北斗三号系统的星载铷频标,短期稳定度达到6.1×10−13 τ −1/2 [6 ] .本实验室郝强等[7 ] 设计出一种铷频标桌面系统,获得了2.4×10−13 τ −1/2 (1~100 s)稳定度测试结果.2018年,我们实现了一种铷频标整机,频率稳定度测定为2.1×10−13 τ −1/2 (1~100 s)[8 ] ,与郝强等的结果相当.这些结果表明传统铷频标性能已经逼近新一代激光抽运铷频标,目前已被报道的激光抽运铷频标的最好稳定度指标为1.4×10−13 τ −1/2 (1~100 s)[9 ] .铷频标的频率稳定度能否进一步提升,达到甚至超过激光抽运铷频标的水平,是一个很值得研究的问题. ...
1
... 近几十年来,卫星导航的应用极大促进了铷原子频标(简称铷频标)的发展.早期的铷频标频率稳定度指标在10−11 τ −1/2 水平.1990年代,Riley等[1 ] 为GPS IIR研制星载铷频标,短期稳定度为3×10−12 τ −1/2 .2010年,Dupuis等[2 ] 报道的为GPS IIF系统研制的星载铷频标,短期稳定度提升到1×10−12 τ −1/2 .目前GPS Ⅲ系统的星载铷频标短期稳定度为1×10−12 τ −1/2 [3 ] .Spectratime公司为Galileo系统研制的星载铷频标,短期稳定度为3×10−12 τ −1/2 [4 ] .本实验室长期致力于北斗卫星导航系统星载铷频标研制,用于北斗二号系统的星载铷频标,短期稳定度为3×10−12 τ −1/2 [5 ] ;用于北斗三号系统的星载铷频标,短期稳定度达到6.1×10−13 τ −1/2 [6 ] .本实验室郝强等[7 ] 设计出一种铷频标桌面系统,获得了2.4×10−13 τ −1/2 (1~100 s)稳定度测试结果.2018年,我们实现了一种铷频标整机,频率稳定度测定为2.1×10−13 τ −1/2 (1~100 s)[8 ] ,与郝强等的结果相当.这些结果表明传统铷频标性能已经逼近新一代激光抽运铷频标,目前已被报道的激光抽运铷频标的最好稳定度指标为1.4×10−13 τ −1/2 (1~100 s)[9 ] .铷频标的频率稳定度能否进一步提升,达到甚至超过激光抽运铷频标的水平,是一个很值得研究的问题. ...
1
... 近几十年来,卫星导航的应用极大促进了铷原子频标(简称铷频标)的发展.早期的铷频标频率稳定度指标在10−11 τ −1/2 水平.1990年代,Riley等[1 ] 为GPS IIR研制星载铷频标,短期稳定度为3×10−12 τ −1/2 .2010年,Dupuis等[2 ] 报道的为GPS IIF系统研制的星载铷频标,短期稳定度提升到1×10−12 τ −1/2 .目前GPS Ⅲ系统的星载铷频标短期稳定度为1×10−12 τ −1/2 [3 ] .Spectratime公司为Galileo系统研制的星载铷频标,短期稳定度为3×10−12 τ −1/2 [4 ] .本实验室长期致力于北斗卫星导航系统星载铷频标研制,用于北斗二号系统的星载铷频标,短期稳定度为3×10−12 τ −1/2 [5 ] ;用于北斗三号系统的星载铷频标,短期稳定度达到6.1×10−13 τ −1/2 [6 ] .本实验室郝强等[7 ] 设计出一种铷频标桌面系统,获得了2.4×10−13 τ −1/2 (1~100 s)稳定度测试结果.2018年,我们实现了一种铷频标整机,频率稳定度测定为2.1×10−13 τ −1/2 (1~100 s)[8 ] ,与郝强等的结果相当.这些结果表明传统铷频标性能已经逼近新一代激光抽运铷频标,目前已被报道的激光抽运铷频标的最好稳定度指标为1.4×10−13 τ −1/2 (1~100 s)[9 ] .铷频标的频率稳定度能否进一步提升,达到甚至超过激光抽运铷频标的水平,是一个很值得研究的问题. ...
1
... 近几十年来,卫星导航的应用极大促进了铷原子频标(简称铷频标)的发展.早期的铷频标频率稳定度指标在10−11 τ −1/2 水平.1990年代,Riley等[1 ] 为GPS IIR研制星载铷频标,短期稳定度为3×10−12 τ −1/2 .2010年,Dupuis等[2 ] 报道的为GPS IIF系统研制的星载铷频标,短期稳定度提升到1×10−12 τ −1/2 .目前GPS Ⅲ系统的星载铷频标短期稳定度为1×10−12 τ −1/2 [3 ] .Spectratime公司为Galileo系统研制的星载铷频标,短期稳定度为3×10−12 τ −1/2 [4 ] .本实验室长期致力于北斗卫星导航系统星载铷频标研制,用于北斗二号系统的星载铷频标,短期稳定度为3×10−12 τ −1/2 [5 ] ;用于北斗三号系统的星载铷频标,短期稳定度达到6.1×10−13 τ −1/2 [6 ] .本实验室郝强等[7 ] 设计出一种铷频标桌面系统,获得了2.4×10−13 τ −1/2 (1~100 s)稳定度测试结果.2018年,我们实现了一种铷频标整机,频率稳定度测定为2.1×10−13 τ −1/2 (1~100 s)[8 ] ,与郝强等的结果相当.这些结果表明传统铷频标性能已经逼近新一代激光抽运铷频标,目前已被报道的激光抽运铷频标的最好稳定度指标为1.4×10−13 τ −1/2 (1~100 s)[9 ] .铷频标的频率稳定度能否进一步提升,达到甚至超过激光抽运铷频标的水平,是一个很值得研究的问题. ...
1
... 近几十年来,卫星导航的应用极大促进了铷原子频标(简称铷频标)的发展.早期的铷频标频率稳定度指标在10−11 τ −1/2 水平.1990年代,Riley等[1 ] 为GPS IIR研制星载铷频标,短期稳定度为3×10−12 τ −1/2 .2010年,Dupuis等[2 ] 报道的为GPS IIF系统研制的星载铷频标,短期稳定度提升到1×10−12 τ −1/2 .目前GPS Ⅲ系统的星载铷频标短期稳定度为1×10−12 τ −1/2 [3 ] .Spectratime公司为Galileo系统研制的星载铷频标,短期稳定度为3×10−12 τ −1/2 [4 ] .本实验室长期致力于北斗卫星导航系统星载铷频标研制,用于北斗二号系统的星载铷频标,短期稳定度为3×10−12 τ −1/2 [5 ] ;用于北斗三号系统的星载铷频标,短期稳定度达到6.1×10−13 τ −1/2 [6 ] .本实验室郝强等[7 ] 设计出一种铷频标桌面系统,获得了2.4×10−13 τ −1/2 (1~100 s)稳定度测试结果.2018年,我们实现了一种铷频标整机,频率稳定度测定为2.1×10−13 τ −1/2 (1~100 s)[8 ] ,与郝强等的结果相当.这些结果表明传统铷频标性能已经逼近新一代激光抽运铷频标,目前已被报道的激光抽运铷频标的最好稳定度指标为1.4×10−13 τ −1/2 (1~100 s)[9 ] .铷频标的频率稳定度能否进一步提升,达到甚至超过激光抽运铷频标的水平,是一个很值得研究的问题. ...
用于北斗三号卫星导航系统的星载铷原子钟特性
1
2021
... 近几十年来,卫星导航的应用极大促进了铷原子频标(简称铷频标)的发展.早期的铷频标频率稳定度指标在10−11 τ −1/2 水平.1990年代,Riley等[1 ] 为GPS IIR研制星载铷频标,短期稳定度为3×10−12 τ −1/2 .2010年,Dupuis等[2 ] 报道的为GPS IIF系统研制的星载铷频标,短期稳定度提升到1×10−12 τ −1/2 .目前GPS Ⅲ系统的星载铷频标短期稳定度为1×10−12 τ −1/2 [3 ] .Spectratime公司为Galileo系统研制的星载铷频标,短期稳定度为3×10−12 τ −1/2 [4 ] .本实验室长期致力于北斗卫星导航系统星载铷频标研制,用于北斗二号系统的星载铷频标,短期稳定度为3×10−12 τ −1/2 [5 ] ;用于北斗三号系统的星载铷频标,短期稳定度达到6.1×10−13 τ −1/2 [6 ] .本实验室郝强等[7 ] 设计出一种铷频标桌面系统,获得了2.4×10−13 τ −1/2 (1~100 s)稳定度测试结果.2018年,我们实现了一种铷频标整机,频率稳定度测定为2.1×10−13 τ −1/2 (1~100 s)[8 ] ,与郝强等的结果相当.这些结果表明传统铷频标性能已经逼近新一代激光抽运铷频标,目前已被报道的激光抽运铷频标的最好稳定度指标为1.4×10−13 τ −1/2 (1~100 s)[9 ] .铷频标的频率稳定度能否进一步提升,达到甚至超过激光抽运铷频标的水平,是一个很值得研究的问题. ...
用于北斗三号卫星导航系统的星载铷原子钟特性
1
2021
... 近几十年来,卫星导航的应用极大促进了铷原子频标(简称铷频标)的发展.早期的铷频标频率稳定度指标在10−11 τ −1/2 水平.1990年代,Riley等[1 ] 为GPS IIR研制星载铷频标,短期稳定度为3×10−12 τ −1/2 .2010年,Dupuis等[2 ] 报道的为GPS IIF系统研制的星载铷频标,短期稳定度提升到1×10−12 τ −1/2 .目前GPS Ⅲ系统的星载铷频标短期稳定度为1×10−12 τ −1/2 [3 ] .Spectratime公司为Galileo系统研制的星载铷频标,短期稳定度为3×10−12 τ −1/2 [4 ] .本实验室长期致力于北斗卫星导航系统星载铷频标研制,用于北斗二号系统的星载铷频标,短期稳定度为3×10−12 τ −1/2 [5 ] ;用于北斗三号系统的星载铷频标,短期稳定度达到6.1×10−13 τ −1/2 [6 ] .本实验室郝强等[7 ] 设计出一种铷频标桌面系统,获得了2.4×10−13 τ −1/2 (1~100 s)稳定度测试结果.2018年,我们实现了一种铷频标整机,频率稳定度测定为2.1×10−13 τ −1/2 (1~100 s)[8 ] ,与郝强等的结果相当.这些结果表明传统铷频标性能已经逼近新一代激光抽运铷频标,目前已被报道的激光抽运铷频标的最好稳定度指标为1.4×10−13 τ −1/2 (1~100 s)[9 ] .铷频标的频率稳定度能否进一步提升,达到甚至超过激光抽运铷频标的水平,是一个很值得研究的问题. ...
A physics package for rubidium atomic frequency standard with a short-term stability of 2.4×10- 13 τ-1/2
1
2016
... 近几十年来,卫星导航的应用极大促进了铷原子频标(简称铷频标)的发展.早期的铷频标频率稳定度指标在10−11 τ −1/2 水平.1990年代,Riley等[1 ] 为GPS IIR研制星载铷频标,短期稳定度为3×10−12 τ −1/2 .2010年,Dupuis等[2 ] 报道的为GPS IIF系统研制的星载铷频标,短期稳定度提升到1×10−12 τ −1/2 .目前GPS Ⅲ系统的星载铷频标短期稳定度为1×10−12 τ −1/2 [3 ] .Spectratime公司为Galileo系统研制的星载铷频标,短期稳定度为3×10−12 τ −1/2 [4 ] .本实验室长期致力于北斗卫星导航系统星载铷频标研制,用于北斗二号系统的星载铷频标,短期稳定度为3×10−12 τ −1/2 [5 ] ;用于北斗三号系统的星载铷频标,短期稳定度达到6.1×10−13 τ −1/2 [6 ] .本实验室郝强等[7 ] 设计出一种铷频标桌面系统,获得了2.4×10−13 τ −1/2 (1~100 s)稳定度测试结果.2018年,我们实现了一种铷频标整机,频率稳定度测定为2.1×10−13 τ −1/2 (1~100 s)[8 ] ,与郝强等的结果相当.这些结果表明传统铷频标性能已经逼近新一代激光抽运铷频标,目前已被报道的激光抽运铷频标的最好稳定度指标为1.4×10−13 τ −1/2 (1~100 s)[9 ] .铷频标的频率稳定度能否进一步提升,达到甚至超过激光抽运铷频标的水平,是一个很值得研究的问题. ...
3
... 近几十年来,卫星导航的应用极大促进了铷原子频标(简称铷频标)的发展.早期的铷频标频率稳定度指标在10−11 τ −1/2 水平.1990年代,Riley等[1 ] 为GPS IIR研制星载铷频标,短期稳定度为3×10−12 τ −1/2 .2010年,Dupuis等[2 ] 报道的为GPS IIF系统研制的星载铷频标,短期稳定度提升到1×10−12 τ −1/2 .目前GPS Ⅲ系统的星载铷频标短期稳定度为1×10−12 τ −1/2 [3 ] .Spectratime公司为Galileo系统研制的星载铷频标,短期稳定度为3×10−12 τ −1/2 [4 ] .本实验室长期致力于北斗卫星导航系统星载铷频标研制,用于北斗二号系统的星载铷频标,短期稳定度为3×10−12 τ −1/2 [5 ] ;用于北斗三号系统的星载铷频标,短期稳定度达到6.1×10−13 τ −1/2 [6 ] .本实验室郝强等[7 ] 设计出一种铷频标桌面系统,获得了2.4×10−13 τ −1/2 (1~100 s)稳定度测试结果.2018年,我们实现了一种铷频标整机,频率稳定度测定为2.1×10−13 τ −1/2 (1~100 s)[8 ] ,与郝强等的结果相当.这些结果表明传统铷频标性能已经逼近新一代激光抽运铷频标,目前已被报道的激光抽运铷频标的最好稳定度指标为1.4×10−13 τ −1/2 (1~100 s)[9 ] .铷频标的频率稳定度能否进一步提升,达到甚至超过激光抽运铷频标的水平,是一个很值得研究的问题. ...
... 铷频标的频率稳定度主要决定于物理系统产生的原子鉴频信号的信噪比和锁频环路的电子学噪声,主要难点是前者.最近,我们在文献[8 ] 工作的基础上,设计了一种新结构物理系统,实测了原子鉴频信号的信噪比和鉴频斜率,据此计算出物理系统散弹噪声极限稳定度为7.5×10−14 τ −1/2 .该结果表明,从物理系统设计角度看,铷频标频率稳定度突破1×10−13 τ −1/2 是完全可能的. ...
... 为降低散弹噪声,本文采用了光学滤光和同位素滤光两级滤光方案.光学滤光的作用是滤除光谱灯中启辉气体(本实验中为Xe气)发光.这种光谱成分对铷原子光抽运没有贡献,仅贡献为散弹噪声.同位素滤光的作用是滤除光谱灯铷发光光谱中的无用成分,这部分光也仅贡献为散弹噪声.为了提高同位素滤光效率,采用了吸收泡和滤光泡分别独立温控的设计方案.在我们先前的设计中,吸收泡和滤光泡均在微波腔内,共用一个温度控制器[8 ] .这种设计的优点是系统的集成度较高,缺点是滤光泡温度不能独立调节,这会导致同位素滤光不完全,抽运光中仍含有较多无用光成分,形成散弹噪声[11 ] . ...
et al, Compact high-performance continuous-wave double-resonance rubidium standard with 1.4×10-13 τ-1/2 stability
1
2014
... 近几十年来,卫星导航的应用极大促进了铷原子频标(简称铷频标)的发展.早期的铷频标频率稳定度指标在10−11 τ −1/2 水平.1990年代,Riley等[1 ] 为GPS IIR研制星载铷频标,短期稳定度为3×10−12 τ −1/2 .2010年,Dupuis等[2 ] 报道的为GPS IIF系统研制的星载铷频标,短期稳定度提升到1×10−12 τ −1/2 .目前GPS Ⅲ系统的星载铷频标短期稳定度为1×10−12 τ −1/2 [3 ] .Spectratime公司为Galileo系统研制的星载铷频标,短期稳定度为3×10−12 τ −1/2 [4 ] .本实验室长期致力于北斗卫星导航系统星载铷频标研制,用于北斗二号系统的星载铷频标,短期稳定度为3×10−12 τ −1/2 [5 ] ;用于北斗三号系统的星载铷频标,短期稳定度达到6.1×10−13 τ −1/2 [6 ] .本实验室郝强等[7 ] 设计出一种铷频标桌面系统,获得了2.4×10−13 τ −1/2 (1~100 s)稳定度测试结果.2018年,我们实现了一种铷频标整机,频率稳定度测定为2.1×10−13 τ −1/2 (1~100 s)[8 ] ,与郝强等的结果相当.这些结果表明传统铷频标性能已经逼近新一代激光抽运铷频标,目前已被报道的激光抽运铷频标的最好稳定度指标为1.4×10−13 τ −1/2 (1~100 s)[9 ] .铷频标的频率稳定度能否进一步提升,达到甚至超过激光抽运铷频标的水平,是一个很值得研究的问题. ...
On the signal-to-noise ratio and short-term stability of passive rubidium frequency standards
1
1981
... 物理系统的散弹噪声极限稳定度可表达为[10 ] : ...
基于开槽管腔的高信噪比铷原子钟物理系统
1
2016
... 为降低散弹噪声,本文采用了光学滤光和同位素滤光两级滤光方案.光学滤光的作用是滤除光谱灯中启辉气体(本实验中为Xe气)发光.这种光谱成分对铷原子光抽运没有贡献,仅贡献为散弹噪声.同位素滤光的作用是滤除光谱灯铷发光光谱中的无用成分,这部分光也仅贡献为散弹噪声.为了提高同位素滤光效率,采用了吸收泡和滤光泡分别独立温控的设计方案.在我们先前的设计中,吸收泡和滤光泡均在微波腔内,共用一个温度控制器[8 ] .这种设计的优点是系统的集成度较高,缺点是滤光泡温度不能独立调节,这会导致同位素滤光不完全,抽运光中仍含有较多无用光成分,形成散弹噪声[11 ] . ...
基于开槽管腔的高信噪比铷原子钟物理系统
1
2016
... 为降低散弹噪声,本文采用了光学滤光和同位素滤光两级滤光方案.光学滤光的作用是滤除光谱灯中启辉气体(本实验中为Xe气)发光.这种光谱成分对铷原子光抽运没有贡献,仅贡献为散弹噪声.同位素滤光的作用是滤除光谱灯铷发光光谱中的无用成分,这部分光也仅贡献为散弹噪声.为了提高同位素滤光效率,采用了吸收泡和滤光泡分别独立温控的设计方案.在我们先前的设计中,吸收泡和滤光泡均在微波腔内,共用一个温度控制器[8 ] .这种设计的优点是系统的集成度较高,缺点是滤光泡温度不能独立调节,这会导致同位素滤光不完全,抽运光中仍含有较多无用光成分,形成散弹噪声[11 ] . ...
Pulsed optically pumped 87 Rb vapor cell frequency standard: A multilevel approach
1
2009
... 为了使更多的原子参与双共振跃迁,提高原子的利用率,需要对光束进行准直,使其变为准平行光,且光束尽可能充满整个吸收泡.光束准直不能简单采用长焦距透镜,焦距过长会导致光的利用率过低,影响抽运效果.焦距过短,则光束准直更加困难.为了兼顾这一矛盾,我们选用了直径为25 mm、焦距为25.8 mm的透镜.考虑到灯泡的体光源特性,灯泡不能严格放置在透镜焦点位置,而应根据光束的准直效果优化选取.图 2 给出了灯泡与透镜之间的距离优化以后光路各处光斑等效直径(用光强半高宽定义)测量结果.由图 2 可见,在吸收泡入光面、出光面和光电池处(参见图 1 ),光斑等效直径基本不变,约为20 mm,略小于吸收泡内径27 mm.吸收泡内靠近泡壁处的铷原子由于壁弛豫效应存在较大的谱线增宽[12 ] ,不是理想的工作物质,因此光斑直径略小于吸收泡内径的设计是合理的. ...
1
... 微波腔采用本实验室发明的开槽管式微波腔[13 ] ,腔内径为30 mm,可以容纳外径为30 mm的吸收泡.微波腔内驻波场的特性直接影响钟跃迁信号强度.根据量子力学原理,只有平行于量子化轴(一般为腔轴)的微波场磁分量,才能够激励铷原子的钟跃迁.因此,微波腔特性用反映微波腔内钟跃迁频率处的驻波场磁场分量与量子化轴平行程度的方向因子ξ 表征,它定义为在腔内微波与原子作用区中,沿量子化轴方向的磁场能量与总磁场能量之比[14 ] : ...
Compact microwave cavity for high performance rubidium frequency standards
2
2012
... 微波腔采用本实验室发明的开槽管式微波腔[13 ] ,腔内径为30 mm,可以容纳外径为30 mm的吸收泡.微波腔内驻波场的特性直接影响钟跃迁信号强度.根据量子力学原理,只有平行于量子化轴(一般为腔轴)的微波场磁分量,才能够激励铷原子的钟跃迁.因此,微波腔特性用反映微波腔内钟跃迁频率处的驻波场磁场分量与量子化轴平行程度的方向因子ξ 表征,它定义为在腔内微波与原子作用区中,沿量子化轴方向的磁场能量与总磁场能量之比[14 ] : ...
... 微波腔内的微波场分布和方向因子可以借助有限元软件HFSS仿真计算得到,方向因子还可以通过测量的87 Rb原子基态5S1/2 超精细Zeeman子能级跃迁谱获得[14 ] .磁场分布示于图 3(a) ,可以看出,腔内磁场能量集中于吸收泡所处区域,且磁场高度平行于量子化轴,计算了图 3(a) 中红色虚线区域内的方向因子为0.94.图 3(b) 为实验测量得到的87 Rb原子Zeeman子能级跃迁谱.可以看出全部7条跃迁谱线中,微波场平行分量激励的σ 跃迁谱线强度远大于垂直分量激励的π跃迁谱线强度,表明微波场中平行于量子化轴的部分为主要成分.设谱中心的σ 跃迁(即钟跃迁)谱线强度为I σ I π r I π l ξ = I σ / ( I σ + I π r + I π l ) . 由此得到方向因子ξ 的实测值为0.87, 与仿真结果一致.高ξ 值微波腔的应用对于增强87 Rb原子的钟跃迁信号是有利的. ...