在世界范围内，尤其是低收入国家，心血管疾病（cardiovascular disease，CVD）仍然是导致死亡的主要原因^[1].在过去20年里，CVD也一直是我国城市和农村地区人口死亡的主要原因之一^[2].如何有效预防和治疗CVD刻不容缓.左心室（left ventricle，LV）是心脏泵血功能最重要的腔室，其心肌壁最厚、心肌收缩力最强.定量评估LV收缩功能，能够辅助诊断心血管疾病，如缺血性心脏病.

临床检查心血管病的影像学手段包括心血管造影（angiocardiography）、超声心动图（echocardiography）、计算机断层扫描（computed tomography，CT）、磁共振成像（magnetic resonance imaging，MRI）等.其中，心脏MRI除具有任意成像平面、心肌血流对比度高等独特优势外，还能提供精确的心脏结构和功能信息^[3].例如，心脏电影磁共振成像（cardiac cine MRI，CCMRI）因其高空间分辨率被广泛用于射血分数（ejection fraction，EF）、腔室体积、心肌质量等的临床测量.它还是无创量化心脏整体功能的金标准^[4].CCMRI的时间分辨率也足够高，可以观察心脏周期运动.CCMRI可提供心脏解剖结构，而标记磁共振成像（tagged MRI，TMRI）^[5]则是心脏MRI的功能成像类型.TMRI图像的网格变化直观记录心肌形变，通常被视为二维层面评估心肌存活质量的金标准.Chen等^[6]利用Gabor滤波器检测标记网格点，运用鲁棒点匹配策略追踪网格点运动.Li等^[7]利用图割算法对Gabor滤波器检测到的网格点分类，运用有限差分法直接从分类网格点中计算双心室三维形变.但TMRI图像分辨率较低，而且网格线会随着时间增长逐渐暗淡，影响运动末期的参数提取.Yu等^[8]提出结合稀疏先验约束的形变模型，该模型在TMRI图像质量较差、噪声较多的情况下，能够较好处理异常值和严重错误.其他用于心室功能分析的MRI技术包括相位对比、位移编码和应变编码MRI，它们共同的缺点是在检查时须获得专门的图像数据集，增加了检查时间，且不能对现有的心脏磁共振数据集进行回顾性应用^[9].

从心脏磁共振图像中评估心脏功能的前提一般是追踪心脏运动以及恢复位移场.传统的运动追踪方法包括基于轮廓特征的方法、形变配准和光流法等.Shi等^[10]提倡把有实际物理意义的连续介质力学原理纳入到心脏运动估计框架中，一方面基于轮廓点局部曲面在较小时间间隔发生微小形变的假设估计轮廓点最佳映射；另一方面把相位对比MRI融入CCMRI图像中，作为LV室壁中运动的补充信息，实现更加健壮完善的追踪结果.Remme等^[11]建立平面有限元网格模拟LV室壁的几何变化：首先追踪标记的轮廓点运动；然后将运动结果与网格拟合，恢复LV三维形变；最后从TMRI图像中导出运动分布模型对原始形变进行滤波，得到更加精确的结果.Veress等^[12]提出超弹性翘曲（hyperelastic warping，HW）方法，利用增广拉格朗日技术实现图像能量硬约束最小化，同时利用超弹性应变能量对图像配准实施软约束.后者用来描述LV真实的本构模型，该模型结合有限元离散化确保形变是微分同胚的，有利于追踪心肌大范围形变与旋转运动.心肌的近似不可压缩性表现为心肌在有血流灌注情况下的体积变化不超过原体积的4%.Bistoquet等^[13]将这一特性作为相邻帧结点匹配应当遵循的约束条件，同时结合归一化互信息配准法在LV中间面曲线坐标系中恢复LV三维周期运动.Liu等^[14]利用状态空间分析技术构建和整合心肌系统动力学、图像观测数据、以及处理和测量噪声干扰.有实际物理意义的力学约束不仅作为心肌形变先验，而且插值和滤波图像观测数据，另外利用携带时空约束的统计滤波理论促进合并多帧信息，以产生最优的心脏运动估计.心脏功能分析大多源于单一的功能或者结构图像，为了更好地表征特异的心脏生理病理，Wong等^[15]利用心脏生理组模型有效融合差异较大的不同图像源信息，这些图像源包括CCMRI图像的观测位移场和体表电位图提供的心脏电生理时空特征，两者互补可得到更加可靠准确的心脏功能分析结果.

目前，基于深度学习的运动追踪存在挑战，因为需要异类数据训练模型泛化能力，而且真实的LV位移场几乎不可能获取.Qiao等^[16]等比较了传统配准和卷积神经网络追踪心脏运动的性能，发现配准方法性能更为稳定，但耗时更长；而神经网络依赖训练数据，例如从健康志愿者队列训练得到的模型用于追踪病患心脏运动，相比传统配准，其性能会显著降低.Tang等^[17]构建密集连接Siamese卷积网络，该网络基于L2代价函数学习匹配最相似的LV局部面片特征.Zhang等^[18]利用循环神经网络提取LV局部运动特征，并采用全连接网络识别心肌梗死区域.循环神经网络的训练和验证金标准是延迟钆增强MRI确定的心肌梗死区域.Zheng等^[19]提出基于半监督学习的心脏病理分类模型，该模型可根据心肌节段半径和厚度特征区分不同类型的心血管疾病.而Mantilla等^[20]采用字典学习区分LV运动正常与否，判断的关键特征是局部径向时空轮廓.

从图像中观测的位移场因噪声干扰显得稀疏杂乱.为了恢复密集规律的位移场，有必要加入正则模型规范位移场秩序，例如提供平滑约束的自由形式形变（free form deformation，FFD）^[21]和统计LV形变特征的主动形状模型（active shape model，ASM）^[22].但本文作者认为单凭图像特征获取的心脏运动参数是不太可靠的，这是由CCMRI携带运动信息稀疏所致.深度学习在医学图像分割领域展示了强大的性能^{[23, 24]}，但应用于心脏运动追踪时存在局限性，因为没有一个统一严格的学习标签供机器训练^[16-18].多图像源数据的互补^{[10, 11, 15]}有利于实现更加准确完善的运动追踪结果，但临床更加倾向于常规的CCMRI检查，CCMRI图像精细的解剖结构更易被患者和医生采纳，TMRI^[6-8]更多地被用作科研序列.医生可能更在意的是描述心肌局部运动和形变的各种功能参数，以便辅助诊断心血管疾病，而非直接的分类结果^{[19, 20]}，这些参数无法由人眼视觉和临床经验直接得到.

本文采用描述LV心肌材质属性的生物力学模型（biomechanical model，BM）^[25]，这与文献^[12-14]的研究思路类似，希望重建的LV位移场更符合实际的LV运动特征.具体做法是将生物力学模型与从心脏电影磁共振图像中观测的位移场共同纳入贝叶斯估计框架，然后采用有限元法求解力学模型引导下的优化位移场.本文首先详细介绍LV位移场重建流程，然后利用实验验证了本文所提方法的有效性.

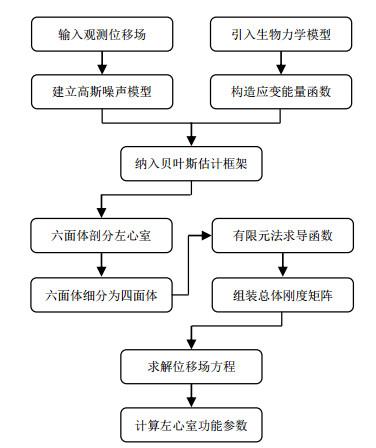
本文结合描述LV心肌材质属性的生物力学模型和心脏电影磁共振图像的观测位移场信息，重建LV完整位移场，整个方法流程如图 1所示.首先根据观测位移场中的轮廓点位移向量和置信度构造观测位移场的高斯噪声模型.在应变能量函数中引入左心肌材质矩阵，以便将LV应变和形变势能联系起来.然后将能量项和噪声项纳入贝叶斯估计（Bayesian estimation）框架.为了求解优化位移场，先对LV六面体剖分和四面体细分；再根据有限元理论，以矩阵形式重写位移场方程，以便求出方程的一阶导函数及LV总体刚度矩阵.最后以一定的迭代次数优化观测位移场，根据最终得到的LV优化位移场，计算LV功能参数.

LV观测位移场并非实际位移场，它会因成像缺陷、算法误差等干扰因素而存在高斯噪声^[26].假设从图像中获取观测位移场的概率呈零均值正态分布，可建立如(1)式所示的高斯噪声模型（Gaussian noise model）.

(1)$ p({u^m}|u) = \frac{1}{{\sqrt {{\text{π }}{\sigma ^2}} }}{{\text{e}}^{\frac{{ - {{(u - {u^m})}^2}}}{{{\sigma ^2}}}}} $

其中，$ {u^m} $和u分别是观测位移场和实际位移场，方差$ {\sigma ^2} $是置信度$ {c^m} $的倒数.置信度$ {c^m} $取决于匹配最佳性$ {m_{\text{b}}} $和唯一性$ {m_{\text{u}}} $^[27].$ {m_{\text{b}}} $和$ {m_{\text{u}}} $与LV弯曲能量（bend energy）有关，弯曲能量的定义如(2)式所示.

(2)$ {\varepsilon _{{\text{be}}}}({p_1}, {p_2}) = \frac{{{k_{\min }}({p_1}, {p_2}) + {k_{\max }}({p_1}, {p_2})}}{2} $

其中，$ {p_1} $和$ {p_2} $分别是当前帧LV轮廓点（以下简称轮廓点）和当前帧轮廓点在下帧位移范围内的轮廓点.$ {k_{\min }} $和$ {k_{\max }} $分别是两点的最小主曲率和最大主曲率差的平方.当前帧轮廓点$ {p_1} $的观测位移$ {u^m} $是基于轮廓点在很短的时间内局部曲面势能变化很小的假设而决定的，如(3)式所示.

(3)$ \begin{gathered} {u^m} = {{\hat p}_2} - {p_1} \hfill \\ {{\hat p}_2} = \mathop {\arg \min }\limits_{{p_2} \in w} {\varepsilon _{{\text{be}}}}({p_1}, {p_2}) \hfill \\ \end{gathered} $

其中，w是当前帧轮廓点$ {p_1} $在下帧的一定位移范围.$ {\hat p_2} $是与$ {p_1} $弯曲能量最小的匹配点.同时，该两点的弯曲能量也就是$ {p_1} $的匹配最佳性$ {m_{\text{b}}} $，如(4)式所示：

(4)$ {m_{\text{b}}}({p_1}) = {\varepsilon _{{\text{be}}}}({p_1}, {\hat p_2}) $

最佳性$ {m_{\text{b}}} $表明两点的曲面势能越接近，匹配可信度越高.唯一性$ {m_{\text{u}}} $在最佳性$ {m_{\text{b}}} $的基础上，要求$ {\hat p_2} $与$ {p_1} $的弯曲能量是位移范围内比其它弯曲能量小得多的值，其定义如(5)式所示：

(5)$ {m_{\text{u}}}({p_1}) = \frac{{{\varepsilon _{{\text{be}}}}({p_1}, {{\hat p}_2})}}{{{{\bar \varepsilon }_{{\text{be}}}} - {\sigma _{{\text{be}}}}}} $

其中，$ {\bar \varepsilon _{{\text{be}}}} $和$ {\sigma _{{\text{be}}}} $分别是除$ {\hat p_2} $外的位移范围内的其它弯曲能量的均值和标准差.由(5)式可知，唯一性$ {m_{\text{u}}} $表明匹配点$ {\hat p_2} $与$ {p_1} $的弯曲能量如果小于位移范围内其它弯曲能量的均值减去标准差，匹配可信度则越高.结合当前帧轮廓点$ {p_1} $的匹配最佳性和唯一性，可以计算其置信度$ {c^m} $，如(6)式所示：

(6)$ {c^m}({p_1}) = \frac{1}{{1 + {m_{\text{b}}}({p_1})}} \times \frac{1}{{1 + {m_{\text{u}}}({p_1})}} $

$ {c^m} $表示当前帧轮廓点$ {p_1} $的匹配置信度，$ {p_1} $的匹配最佳性和唯一性越小，其匹配置信度越高.由上述推导和(1)式可知，建立高斯噪声模型需要观测位移场中的每个轮廓点位移向量$ {u^m} $和匹配置信度$ {c^m} $.这两项参数由基于轮廓形状特征的LV运动追踪方法得到，如图 2所示.该方法流程主要分为(a)分割LV轮廓、(b)建立LV表面模型、(c)提取轮廓局部特征和(d)恢复观测位移场.

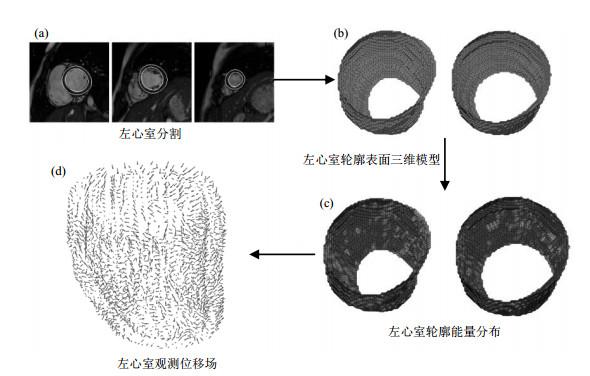
由于本文的追踪方法基于轮廓特征，因此精确的LV分割结果非常重要.心血管成像（circle cardiovascular imaging，CVI）软件提供了稳定且实时的全自动LV分割.但本文定义的LV轮廓是平滑非凹的，但CVI分割的原始轮廓是较为粗糙的，须进一步对轮廓进行闭合检测、细化、平滑等处理.尽管CVI分割LV为本文科研工作提供巨大便利，但处理大量图像难免会产生过分割、欠分割和漏分割个例.本文手动修复了错误分割个例，避免分割错误对功能参数估计的影响.除LV分割流程外，我们的三维建模、运动追踪以及应变分析框架是完全自动稳定的.有些不需要分割直接估计LV运动参数的方法可能忽略了CCMRI图像的一个特性，那就是室中层面的图像帧存在较多的乳头肌和小梁肌，干扰组织的突兀变化可能会导致跟踪结果在解剖学上的不现实，这也是本文要求分割轮廓尽可能是凸的原因.此外，如果需要评估不同心肌节段的功能参数，首要条件是分割LV，然后依据美国心脏协会制定的左心肌分段标准再次细分LV.图 2(b)表面模型生成包括轮廓层间插值，以弥补层间分辨率小于层内分辨率的差距，以及用三角面片表达轮廓点局部特征，该特征作为运动追踪的标记，如图 2(c)所示.根据文献^[10]提供的薄板弹性能量在瞬时变化微小的假设完成前后帧轮廓点的匹配，最终得到LV观测位移场，如图 2(d)所示.

物体形变产生的内能变化可采用基于连续介质力学的应变能量函数表示^[28].该函数不考虑刚体运动如平移、旋转等对物体形变的影响，如(7)式所示.

(7)$ W = {{\bf{E}}^{\text{t}}}{\bf{DE}} $

其中，D是物体材质属性矩阵，它将物体的应变E同物体内能W联系起来.应变E是由三个正应变和三个剪应变组成的列向量，反映了物体的形变程度和类型^[29].本文采用的生物力学模型是将LV心肌看成横向各向同性材质，考虑了肌纤维方向的优先刚度，其材质矩阵D的逆矩阵如(8)式所示.

(8)$ {{\bf{D}}^{ - 1}} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{{{E_p}}}}&{\frac{{ - {v_p}}}{{{E_p}}}}&{\frac{{ - {v_{fp}}}}{{{E_f}}}}&0&0&0 \\ {\frac{{ - {v_p}}}{{{E_p}}}}&{\frac{1}{{{E_p}}}}&{\frac{{ - {v_{fp}}}}{{{E_f}}}}&0&0&0 \\ {\frac{{ - {v_{fp}}{E_f}}}{{{E_p}}}}&{\frac{{ - {v_{fp}}{E_f}}}{{{E_p}}}}&{\frac{1}{{{E_f}}}}&0&0&0 \\ 0&0&0&{\frac{{2(1 + {v_p})}}{{{E_p}}}}&0&0 \\ 0&0&0&0&{\frac{1}{{{G_f}}}}&0 \\ 0&0&0&0&0&{\frac{1}{{{G_f}}}} \end{array}} \right] $

其中，$ {E_f} $为纤维方向刚度，$ {E_p} $为垂直纤维方向刚度，$ {v_{fp}} $和$ {v_p} $分别是对应的泊松比.$ {G_f} $是垂直纤维方向的剪切模量，$ {G_f} \approx {E_f}/[2(1 + {v_{fp}})] $.当$ {E_f} $和$ {E_p} $、$ {v_{fp}} $和$ {v_p} $相等时，D简化为更为常见的各向同性模型.

接着，需要把应变能量函数转化为贝叶斯估计中的先验概率.物体在某一点处是否发生形变是通过与它相邻质点的相对位置变化体现的.而应变能量函数通过应变E反映了某点处的形变势能，即某点应变能量由该点与邻域点在物体运动前后的位置关系决定.概率密度函数中类似的是马尔科夫随机场（Markov random field），场中某点的概率值由邻域点决定^[30].因此，应变能量函数的概率形式可写为：

(9)$ p(u) = k{{\text{e}}^{ - W(u)}} $

其中，k为归一化常量.

以贝叶斯估计形式将图像观测位移场与生物力学模型结合起来，重建LV完整位移场.即把观测位移场的高斯噪声模型和引入LV心肌材质属性的应变能量函数共同纳入贝叶斯估计框架中，如(10)式所示.

(10)$ \hat u = \mathop {\arg \max }\limits_u p(u|{u^m}) = \frac{{p({u^m}|u)p(u)}}{{p({u^m})}} $

$ p({u^m}|u) $表示当原始位移场为u时，从图像中得到观测位移场$ {u^m} $的概率，由高斯噪声模型决定.$ p(u) $是关于原始位移场u的先验概率，取决于生物力学模型.$ p(u|{u^m}) $是后验概率，表示当观测位移场为$ {u^m} $时，获得原始位移场u的概率.首先对贝叶斯估计方程取对数，并忽略常数项$ p({u^m}) $可得：

(11)$ \hat u = \mathop {\arg \max }\limits_u [\ln p({u^m}|u) + \ln p(u)] $

接着，将(1)式和(9)式代入(11)式，省去符号，忽略常数项和不包含u的项，可得：

(12)$ \hat u = \mathop {\arg \max }\limits_u \left[ {W(u) + \frac{{{{(u - {u^m})}^2}}}{{{\sigma ^2}}}} \right] $

最后，采用有限元法求解位移场方程之前，需要先对LV进行有限元剖分.

有限元剖分可以逼近LV复杂的几何形状.本文先采用对称最近邻法连接同一层面的LV轮廓点（包括心内膜、心肌和心外膜轮廓），对称最近邻点对的关系表达式为：

(13)$ \begin{gathered} q = \arg \mathop {\min }\limits_{{q_i}} d(p, {q_i}) \hfill \\ p = \arg \mathop {\min }\limits_{{p_j}} d(q, {p_j}) \hfill \\ \end{gathered} $

其中，d是欧式距离算子，i和j表示不同轮廓类型的点索引.如果点p的最近邻点为q，同时点q的最近邻点为p，那么p和q的关系是对称最近邻.接着，以自下而上的方式（从心尖到心底的顺序）进行同一轮廓类型的点采样，采样方案如下：

(14)$ sci = {\rm{int}} \frac{{rcp}}{{rscp}} + cpi $

其中，rcp和rscp分别表示剩余轮廓点数和剩余采样轮廓点数，int为取整运算符，cpi和sci分别表示当前轮廓点索引和采样轮廓点索引.最后，配对不同轮廓类型的采样轮廓点，配对方案如下：

(15)$ Emp(p, q) = \arg \mathop {\min }\limits_{{q_i}} ds(p, {q_i}) $

其中，ds是以p和$ {q_i} $为起始点对的欧式距离和算子，Emp表示使得所有配对轮廓点欧式距离和最小的起始点对.上述步骤分别完成了不同轮廓类型的点连接，同一轮廓类型的点采样以及不同轮廓类型的点配对，最终得到紧密连接的LV六面体网格，如图 3所示.

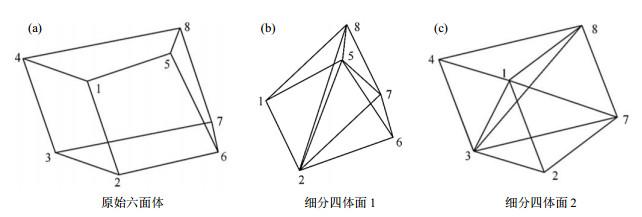
本文将六面体网格的8个结点进行编号，如图 4(a)所示.四面体网格是在六面体网格的基础上继续细分，以六面体网格结点编号为参考，四面体网格结点编号方式有6种，分别为（1-2-5-8）、（2-5-7-8）、（2-5-6-7）、（1-3-4-8）、（1-3-7-8）、（1-2-3-7）.根据上述编号方式，可以将一个六面体网格继续剖分为6个四面体网格，如图 4(b)和4(c)所示.LV剖分过程中可能会出现病态四面体、退化四面体，这是不良结构，影响形变参数的提取，而且剖分过程没有考虑到患者LV的特异性.文献^[31]提供了一种无网格法可用于解决心脏大形变，材质不均匀等困难，这将是本文应变分析模块的改进方向.

有限元法中的离散化步骤是利用形状函数将结点位移和单元的内位移联系起来.四面体单元内一点的位移可由4个结点的形状函数和结点位移来表示.

(16)$ {u^{{\text{int}}}} = \sum\limits_{i = 1}^4 {{N_i}{\bf{u}}_i^{{\text{nod}}}} $

其中，$ {N_i} $和$ {\bf{u}}_i^{{\text{nod}}} $分别是结点i的的形状函数和位移向量，$ {u^{{\text{int}}}} $是四面体单元内一点的插值位移.四面体单元内一点的应变是由结点的形状函数与结点位移的乘积经微分运算而得到.据此可以计算LV所有四面体单元总的应变能量，如(17)式所示.

(17)$ W(u) = \sum\limits_{i = 1}^n {\int\limits_{{v_i}} {{\bf{E}}_i^{\text{t}}{\bf{D}}{{\bf{E}}_i}} } {\text{d}}{v_i} $

其中，i是四面体单元索引，$ {v_i} $是四面体单元体积.应变列向量$ {{\bf{E}}_i} $是由应变矩阵$ {{\bf{B}}_i} $与第i个四面体单元所有结点位移组成的位移列向量$ {\bf{u}}_i^{{\text{nod}}} $相乘而得到.由此(17)式可变换为：

(18)$ W(u) = \sum\limits_{i = 1}^n {\int\limits_{{v_i}} {{{({\bf{u}}_i^{{\text{nod}}})}^{\text{t}}}{\bf{{\rm B}}}_i^{\text{t}}{\bf{D}}{{\bf{B}}_i}} } {\bf{u}}_i^{{\text{nod}}}{\text{d}}{v_i} $

根据有限元理论，可从(18)式中获取总体刚度矩阵K：

(19)$ {\bf{K}} = \sum\limits_{i = 1}^n {\int\limits_{{v_i}} {{{\bf{B}}}_i^{\text{t}}{\bf{D}}{{\bf{B}}_i}} } {\text{d}}{v_i} $

将LV四面体单元的所有结点位移以列向量形式连接，即$ {{\bf{U}}^{\text{t}}} = [{u_{1x}}, {u_{1y}}, {u_{1z}}, ..., {u_{nx}}, {u_{ny}}, {u_{nz}}] $，其中，n是结点数量，x、y、z表示坐标轴方向.将结点位移场U和总体刚度矩阵K代入(18)式，那么总的应变能量以矩阵形式表示为：

(20)$ W({\bf{U}}) = {{\bf{U}}^{\text{t}}}{\bf{KU}} $

其中，U是四面体单元结点的原始位移场.再把所有结点的观测位移场也以列向量形式连接，即$ {\bf{U}}_m^{\text{t}} = [u_{_{1x}}^m, u_{_{1y}}^m, u_{_{1z}}^m, ..., u_{_{nx}}^m, u_{_{ny}}^m, u_{_{nz}}^m] $.那么(12)式中的噪声项以矩阵形式表示为：

(21)$ N({\bf{U}}) = {({\bf{U}} - {{\bf{U}}_m})^{\text{t}}}{\bf{C}}({\bf{U}} - {{\bf{U}}_m}) $

其中，C是总体置信度矩阵，为一对角矩阵.将(20)式和(21)式代入(12)式中，得到矩阵形式的贝叶斯估计方程，如(22)式所示.

(22)$ {\bf{\hat U}} = \mathop {\arg \max }\limits_{\bf{U}} \left[ {{{\bf{U}}^{\text{t}}}{\bf{KU}} + {{({\bf{U}} - {{\bf{U}}_m})}^{\text{t}}}{\bf{C}}({\bf{U}} - {{\bf{U}}_m})} \right] $

对(22)式中的U求偏导函数，令导函数值为0，得到估计位移场$ {\bf{\hat U}} $的线性解，如(23)式所示：

(23)$ {\bf{\hat U}} = {({\bf{K}} + {\bf{C}})^{ - 1}}{\bf{C}}{{\bf{U}}_m} $

位移场方程中的观测位移场$ {{\bf{U}}_m} $和总体置信度矩阵C分别由(3)式和(6)式计算.而总体刚度矩阵K是由每个四面体单元刚度矩阵组装而成.本文采用的是四面体常应变单元，各点应变相同，单元刚度矩阵积分后如(24)式所示：

(24)$ {{\bf{K}}_{\text{e}}} = {{\bf{B}}^{\text{t}}}{\bf{DB}}{v_{\text{e}}} $

其中，$ {v_{\text{e}}} $是四面体单元体积.按结点索引分块，单元刚度矩阵表示为：

(25)$ {{\bf{K}}_{\text{e}}} = \left[ {\begin{array}{*{20}{c}} {{{\bf{k}}_{ii}}}&{{{\bf{k}}_{ij}}}&{{{\bf{k}}_{ik}}}&{{{\bf{k}}_{im}}} \\ {{{\bf{k}}_{ji}}}&{{{\bf{k}}_{jj}}}&{{{\bf{k}}_{jk}}}&{{{\bf{k}}_{jm}}} \\ {{{\bf{k}}_{ki}}}&{{{\bf{k}}_{kj}}}&{{{\bf{k}}_{kk}}}&{{{\bf{k}}_{km}}} \\ {{{\bf{k}}_{mi}}}&{{{\bf{k}}_{mj}}}&{{{\bf{k}}_{mk}}}&{{{\bf{k}}_{mm}}} \end{array}} \right] $

其中任一子矩阵为：

(26)$ {{\bf{k}}_{rs}} = {\bf{B}}_r^{\text{t}}{\bf{D}}{{\bf{B}}_s}{v_{\text{e}}} $

其中，r和s是四面体单元结点索引之一（i、j、k、m）.$ {{\bf{B}}_r} $和$ {{\bf{B}}_s} $是对应结点的应变矩阵，矩阵中的每项元素都是由结点坐标决定的常数^[32].将每个$ {{\bf{k}}_{rs}} $按照结点索引顺序投放，最终形成总体刚度矩阵K.把总体刚度矩阵K、总体置信度矩阵C和观测位移场$ {{\bf{U}}_m} $代入(23)式，并以适当的次数迭代求解，将从观测位移场中得到LV优化位移场，如图 5所示.图 5(a)和5(c)分别是收缩和舒张时期的观测位移场，图 5(b)和5(d)分别是收缩和舒张时期对应的优化位移场.仔细观察图 5可以发现，LV优化位移场比原始观测位移场更加密集有序.

本文使用的101例心脏电影磁共振图像数据由46例LV射血无力患者和55例LV射血正常患者组成，射血无力表现为左心室射血分数（LVEF）低于50%.射血正常和射血无力的都是心血管疾病患者（主要是心肌肥厚、心力衰竭、心室重构患者）.患者性别包括35例女性和66例男性，年龄处于14~88岁，心率范围为46~125次/min.磁共振图像在GE 1.5T扫描仪上通过稳态自由进动（steady state free precession，SSFP）成像序列获取，具体成像参数如下：图像矩阵大小为256×256，视野为360 mm ×360 mm，重复时间为3.5 ms，回波时间为1.4 ms，层厚为6~7 mm，层间距为7~10 mm.数据来源于康奈尔医学院，患者已签订知情同意书，通过了上海交通大学医学院附属上海儿童医学中心的伦理审批要求.后续数据处理在MATLAB2020A上完成，LVEF首先是根据生成的LV三维模型，通过convhull函数估计舒张末期与收缩末期体积，然后依据EF公式计算得到.

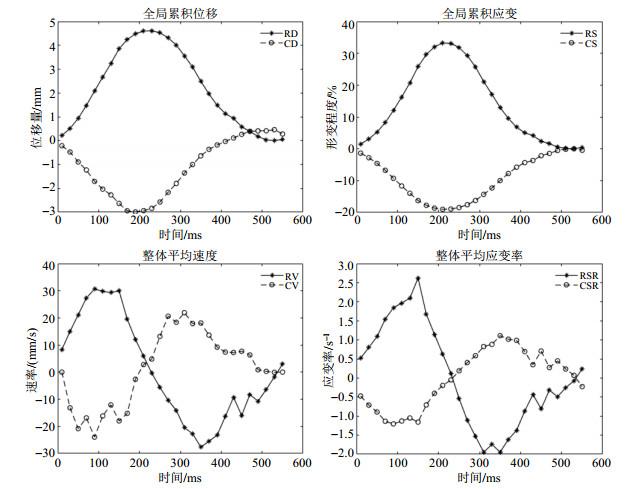
本文从重建的LV位移场中导出了LV功能参数，包括径向位移（radial displacement，RD）和速率（radial velocity，RV）、圆周位移（circumferential displacement，CD）和速率（circumferential velocity，CV），径向应变（radial strain，RS）和应变率（radial strain rate，RSR）、圆周应变（circumferential strain，CS）和应变率（circumferential strain rate，CSR）.RD和RS描述LV的收缩和舒张程度，CD和CS刻画LV的扭转和解旋程度.LV在一个心动周期的全局累积RD和CD曲线如图 6左上所示，全局累积RS和CS曲线如图 6右上所示.全局累积曲线表示LV从舒张末期开始，逐步收缩和扭转，一直到收缩末期的收缩和扭转峰值状态，再逐步舒张和解旋，最终重新回到舒张末期的原始状态.图 6左下的RV和CV曲线表示每帧时间间隔内，LV在径向和圆周方向上的整体运动快慢，图 6右下的RSR和CSR曲线表示每帧时间间隔内，LV在径向和圆周方向上的整体形变快慢.

为了验证本文方法能够有效区分LV收缩运动正常与否，本节比较了LV射血正常组和无力组的LV各功能参数的差异，包括径向和圆周方向上的峰值位移和应变，以及收缩时期的最大速率和应变率（参照图 6各分图收缩期全局峰值点），如表 1所示.

由表 1可知，射血正常组的各项LV功能参数的绝对值要比射血无力组更大，在一定程度上说明LV的EF和其整体收缩能力存在正相关：EF越高，其整体收缩能力也就越强.但也要注意到，由于本文未局部测量LV功能参数，因此射血正常患者的LV功能参数也可能出现偏低的情况.两组各项参数的p值均小于0.001，说明两组的LV功能参数存在非常显著的差异，证明了本文方法能够有效区分LV整体收缩运动正常与否.

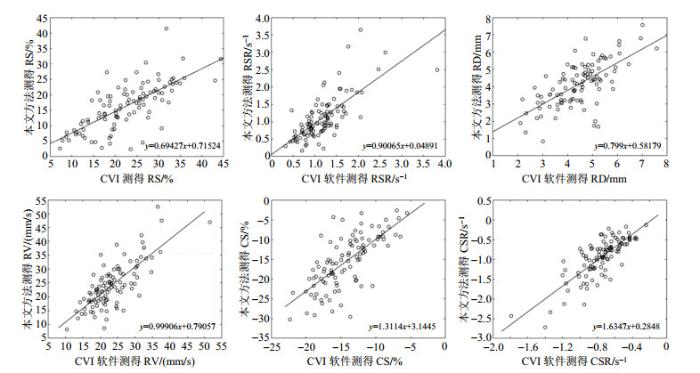
为了进一步验证本文所提方法的临床实用性，将本文方法测量的LV功能参数与心血管成像软件CVI进行相关性分析，该软件较为广泛地应用于临床心脏功能分析以及心血管疾病的科学研究.图 7显示了本文方法测量的101例收缩时期全局峰值参数包括径向应变、应变率、位移、速度以及圆周应变、应变率与CVI软件测量结果的相关性，对应的线性回归方程均在图中标出.RS、RSR、RD、RV、CS、CSR的相关系数R分别为0.718、0.726、0.668、0.765、0.708和0.792，其中CSR的相关性最高.高相关性说明了本文方法与CVI软件的匹配程度较高（0.6~0.8时为强相关）.由于两者测量的圆周位移和速率单位不一致，本文方法为毫米，CVI为弧度，所以这两项参数没有相关性.此外，CVI测量的LV射血正常组和无力组的圆周位移和速率不存在非常显著的差异（详见附件表S1，扫描文章首页OSID二维码，或在网页版获取）.

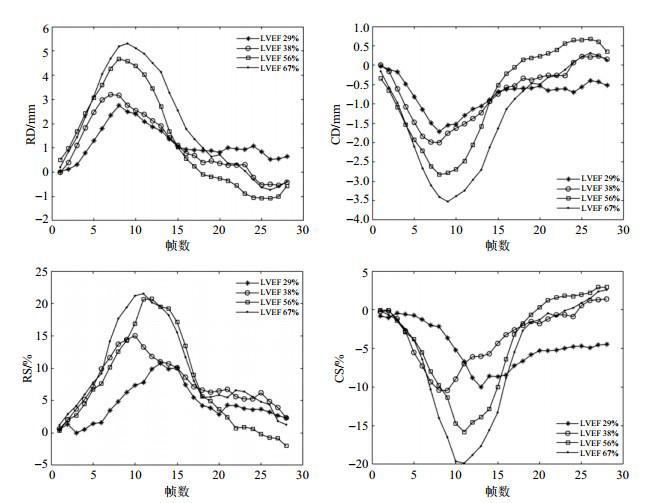
分别随机选取2例临床表现为LV射血无力和射血正常对象，比较他们的RD、RS、CD、CS在整个心动周期的演化趋势，如图 8所示.累积应变和相同方向的累积位移是关系密切的，LVEF也和累积峰值存在一定的相关性，如果不考虑射血分数保留型心衰疾病的话.LVEF越高，功能参数的峰值越大，电影帧表现为心肌增厚量更多.

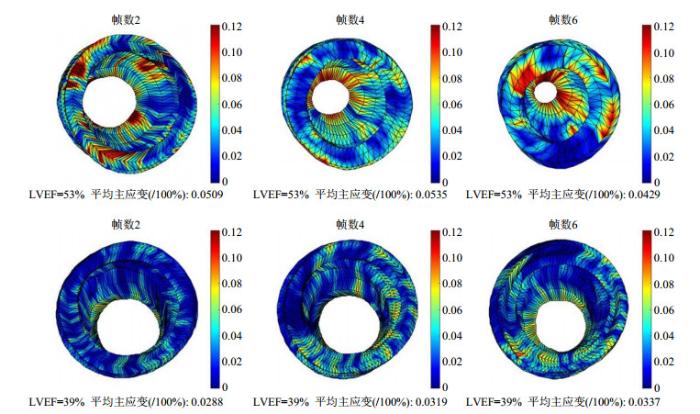
由上述分析可知，LVEF是LV整体功能指标，它和全局累积径向位移、应变存在正相关，和全局累积圆周位移、应变存在负相关.但是心肌可能存在局部运动异常，这可能无法从全局功能参数和LVEF得到.继续观察1例左心室射血正常（LVEF > 50%）与1例射血无力（LVEF < 50%）患者在收缩时期的应变云图，如图 9所示.主应变（颜色棒范围值）是结点径向和圆周应变平方和的正平方根，用来衡量结点局部区域总形变程度，平均主应变是所有结点主应变的和除以所有结点数量.由图 9可知，从局部层面看，收缩阶段的不同帧LV射血正常组大部分心肌节段的形变量明显大于射血无力患者，而且存在较多大形变（红色部分），该形变量是指当前帧到下帧的瞬时变化.此外从整体上看，LV射血正常患者组的结点平均主应变均大于同时刻的射血无力患者.射血正常组的LV形态变化较大，心肌增厚量多，而射血无力患者的LV形态变化小，心肌厚度几乎不变.

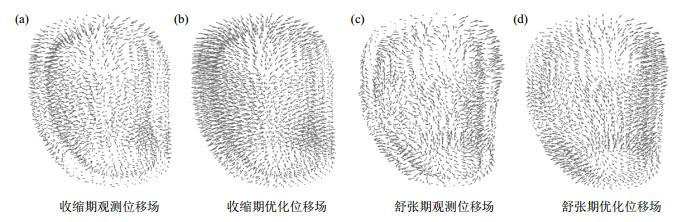
LV位移场在不同约束条件的位移大小和方向会发生变化，其功能参数也会相应变化.101例患者原始位移场、局域平滑位移场和生物力学模型指导位移场的LV功能参数差异如表 2所示.分别对比无约束和模型约束的RS和CS绝对值，可以发现无约束的RS比模型约束的大，CS比模型约束的小，而两者总应变量差不多.因此生物力学模型提供了LV的旋转动力，将更多的形变量分配到周向，增加更多周向位移.平滑约束会稍微降低总形变量.根据进一步实验得出不同约束条件下的射血无力和正常组的LV功能参数绝大部分存在非常显著的差异（详见附件表S1），说明不同类型位移场都可用于区分LV正常与否，证明本文运动追踪方法的可靠性.而生物力学模型更多地是增加LV旋转运动，使位移场演化更符合真实的LV运动.因为真实LV运动是存在解旋和扭转的，这点应从圆周方向的参数看出.追踪算法导出的初始位移场是较为杂乱无章的，力学模型在原始位移场的基础上，增加了一些周向的分量.

为了准确提取心脏电影磁共振图像中的LV运动信息，辅助诊断心血管疾病，本文将描述LV心肌材质属性的生物力学模型作为心脏电影磁共振图像观测位移场的插值项，重建LV优化位移场.具体做法是将两者共同纳入贝叶斯估计框架，然后采用有限元法解位移场方程，最后依据优化位移场，导出LV功能参数.为了验证本文方法能够有效区分LV运动正常与否，本文比较了LV射血正常组和无力组的LV功能参数，发现两组在径向和圆周方向上的位移、速度、应变和应变率均具有非常显著的差异.本文方法还与CVI软件的测量结果具有较高的相关性，说明本文方法有望辅助临床诊疗心血管疾病.