土壤水分的准确检测，对于农业和地质勘探中的水管理至关重要.然而在许多情况下，获得这些参数既费时，又对土壤有侵入性.因此，发展一种快速且非侵入性的方法来测量土壤的水分参数非常必要^[1].过去几十年，不均匀静态磁场的新方法的发展扩大了核磁共振（NMR）的应用范围.基于这些新方法的移动NMR设备在石油工业^{[2, 3]}、水文研究^{[1, 4]}和医学^[5]中有重要的新应用.

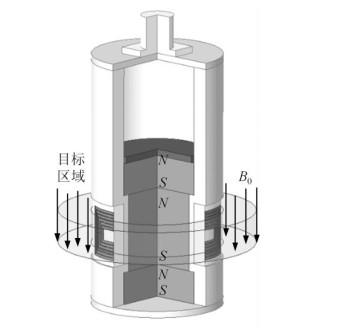
Inside-out测量方式，即测量区域位于传感器外部，可以不受样品尺寸的限制.对于这类结构，国内外已有不少磁体设计和应用.Jackson等^{[6, 7]}提出了两个相同大小的圆柱形磁铁结构，通过磁极相对（即磁体轴心重合，上方磁体N极向下，下方磁体N极向上）产生一个位于仪器外部的静态磁场B₀环形目标区域；位于磁体之间的线圈产生射频场B₁，在环形目标区域内与B₀正交.Taicher等^[8]设计了一个NMR仪器，其圆柱形磁体横向磁化，并且射频线圈沿着磁体的纵向方向包裹，与磁体的圆柱壳同轴.Kleinberg等^[9]提出了三块磁铁以同一方向磁化，与中心的小磁铁平行放置的结构，其目标测量区域为扇形，并沿着轴向具有一定宽度.2011年，Sucre等^[1]提出了测量土壤水分的新仪器，传感器由六个圆柱形磁铁（两个直径较大的和四个直径较小的圆柱体）组成，在磁体阵列中心采用平面矩形射频线圈.2013年，Perlo等^[10]改进了Sucre等的传感器，使用了两个具有横向极化的圆柱形磁铁和五圈矩形射频线圈，经角度位置优化后，射频线圈被放置在磁铁一侧的凹槽中.Marble等^[11]引入了用于单边NMR测量的三磁棒阵列：三个磁块排列成同一方向的磁块，以产生均匀的磁场，磁场与表面平行，设计自然紧凑安全.

本文设计了一个微型Inside-out传感器，结构如图 1所示.该结构结合了Jackson等^[7]提出的环形对称性，以及Marble等^[11]与郭盼等^[12]提出的三磁棒阵列优势，在环形目标区域中产生具有恒定梯度的磁场.四个相同尺寸的弧形螺旋线圈用作射频线圈的激发和检测，采用宽频匹配方法，增加激励区域，从而提高射频线圈的整体信噪比.射频线圈放置位置如图 1所示，优化后的磁体中间部分有一个凹槽，射频线圈放置于该凹槽中，距离中间磁体外表面6.5 mm.线圈轴向总宽度不大于20 mm.下文将详细介绍磁体和射频线圈的设计方案和相关实验结果.

考虑到现场测量的便利性，本文选择Inside-out磁体，磁体由三个同轴且均沿轴向磁化的圆柱形磁体紧密排列而成^[13]，磁体轴心位于z轴上.假设剩磁为B_r的磁体（半径a）上下表面的位置分别为z₂和z₁，将磁体等效成电流形式，电流沿着磁体外周面分布，如图 2所示.

对于图 2中显示的圆柱形磁铁，等效表面电流密度J为^[14]

(1)$J = \frac{{{B_r}}}{{{\mu _0}}}{e_\theta }$

其中，${B_r}$为磁体的剩磁，${\mu _0}$为真空磁导率，${e_\theta }$为周向单位矢量.

上下两个磁体半径相同，均为a，中间磁体半径为a₀，建立圆柱坐标系，三个圆柱形磁体的空间位置及尺寸如图 2（右）所示，则磁体在空间点P$(\rho , z)$产生的磁场为：

(2)$\begin{gathered} {B_\rho } = \frac{{{B_r}}}{{2{\rm{ \mathsf{ π} }}}}\int_{{z_1}}^{{z_2}} {\frac{{z - {z_0}}}{{\rho \sqrt {{{(a + \rho )}^2} + {{(z - {z_0})}^2}} }}\left[ { - K(k) + \frac{{{a^2} + {\rho ^2} + {{(z - {z_0})}^2}}}{{{{(a - \rho )}^2} + {{(z - {z_0})}^2}}}E(k)} \right]\text{d}{z_0}} \\ + \frac{{{B_r}}}{{2{\rm{ \mathsf{ π} }}}}\int_{ - {z_2}}^{ - {z_1}} {\frac{{z - {z_0}}}{{\rho \sqrt {{{(a + \rho )}^2} + {{(z - {z_0})}^2}} }}\left[ { - K(k) + \frac{{{a^2} + {\rho ^2} + {{(z - {z_0})}^2}}}{{{{(a - \rho )}^2} + {{(z - {z_0})}^2}}}E(k)} \right]\text{d}{z_0}} \\ + \frac{{{B_r}}}{{2{\rm{ \mathsf{ π} }}}}\int_{ - {z_1}}^{{z_1}} {\frac{{z - {z_0}}}{{\rho \sqrt {{{({a_0} + \rho )}^2} + {{(z - {z_0})}^2}} }}\left[ { - K(k) + \frac{{a_0^2 + {\rho ^2} + {{(z - {z_0})}^2}}}{{{{({a_0} - \rho )}^2} + {{(z - {z_0})}^2}}}E(k)} \right]\text{d}{z_0}} \\ \end{gathered} $

(3)$\begin{gathered} {B_z} = \frac{{{B_r}}}{{2{\rm{ \mathsf{ π} }}}}\int_{{z_1}}^{{z_2}} {\frac{1}{{\sqrt {{{(a + \rho )}^2} + {{(z - {z_0})}^2}} }}\left[ {K(k) + \frac{{{a^2} - {\rho ^2} - {{(z - {z_0})}^2}}}{{{{(a - \rho )}^2} + {{(z - {z_0})}^2}}}E(k)} \right]\text{d}{z_0}} \\ + \frac{{{B_r}}}{{2{\rm{ \mathsf{ π} }}}}\int_{ - {z_2}}^{ - {z_1}} {\frac{1}{{\sqrt {{{(a + \rho )}^2} + {{(z - {z_0})}^2}} }}\left[ {K(k) + \frac{{{a^2} - {\rho ^2} - {{(z - {z_0})}^2}}}{{{{(a - \rho )}^2} + {{(z - {z_0})}^2}}}E(k)} \right]\text{d}{z_0}} \\ + \frac{{{B_r}}}{{2{\rm{ \mathsf{ π} }}}}\int_{ - {z_1}}^{{z_1}} {\frac{1}{{\sqrt {{{({a_0} + \rho )}^2} + {{(z - {z_0})}^2}} }}\left[ {K(k) + \frac{{a_0^2 - {\rho ^2} - {{(z - {z_0})}^2}}}{{{{({a_0} - \rho )}^2} + {{(z - {z_0})}^2}}}E(k)} \right]\text{d}{z_0}} \\ \end{gathered} $

上式中，$K\left( k \right) = \int_0^{\frac{{\rm{ \mathsf{ π} }}}{2}} {\frac{{{\rm{d}}\alpha }}{{\sqrt {1 - {k^2}{{\sin }^2}\alpha } }}} $，为第一类完全椭圆积分；$E\left( k \right) = \int_0^{\frac{{\rm{ \mathsf{ π} }}}{2}} {\sqrt {1 - {k^2}{{\sin }^2}\alpha } {\rm{d}}\alpha } $，为第二类完全椭圆积分；${k^2} = \frac{{4a\rho }}{{\sqrt {{{\left( {a + \rho } \right)}^2} + {{\left( {z - {z_0}} \right)}^2}} }}$.磁体的尺寸位置为变量（a，${a_0}$，${z_1}$，${z_2}$），P点坐标为$(\rho , z)$，${B_\rho }$为磁场的径向分量，${B_z}$为磁场的轴向分量.对于本文所设计的磁体，目标磁场只有z方向分量.同时，为了能够测量土壤中水分的自扩散特性，希望磁场沿着径向方向线性变化.对于特定带宽的射频线圈，磁场梯度太大会导致激励的样品区域太小，从而导致接收的磁共振信号强度减小.磁场梯度太小又会导致激励的样品区域太大，不容易测量出水分的自扩散特性.考虑到土壤的特性，本文选择的传感器磁场梯度范围在1 T/m~3 T/m.为了小型化考虑，限定传感器的半径在20 mm以内，总长度在100 mm以内.

磁场梯度表示为：

(4)${G_B} = \frac{{\partial {B_z}}}{{\partial \rho }}$

磁场梯度的线性度表示为：

(5)${\eta _{\rm{G}}} = \frac{{\partial {G_B}}}{{\partial \rho }}$

在寻找最优结构参数时，建立非线性优化模型：

(6)$\begin{gathered} \min {f_{\min }}(a, {a_0}, {z_1}, {z_2}) = \sum\limits_{i = 1}^N {{\eta _{{G_{Bi}}}}} \\ s.t. \left\{ \begin{gathered} 1 \leqslant {G_{Bi}} \leqslant 3 \\ 0 < a \leqslant 0.02 \\ 0 < {a_0} \leqslant 0.02 \\ 0 < 2{z_2} \leqslant 0.1 \\ 0 < {z_1} < {z_2} \\ \end{gathered} \right. \\ \end{gathered} $

其中，i表示目标区域内第i个采样点，N表示目标区域内的总采样点数，a、${a_0}$、${z_1}$、${z_2}$单位为m.

采用Matlab软件，经过计算得到的最优结构参数为：端部磁体半径15 mm、高度10 mm；中间磁体的半径13 mm、高度24 mm.图 3为磁体中间区域xoy平面上的磁场分布，磁场梯度为1.99 T/m.

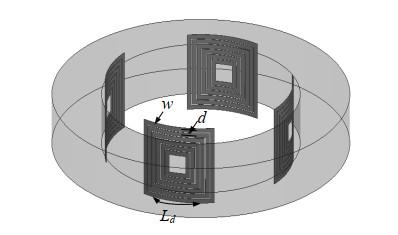
采用弧面螺旋线圈作为射频发射和接收线圈，线圈结构示意图如图 4所示，图中所示线圈结构为其中4个相同尺寸的线圈的结构分布示意图，实际射频线圈由多个相同线圈串联组成，并且沿着圆周方向对称分布.

为了获得最佳的信噪比（SNR），需要对线圈结构参数进行寻优.SNR可以用下式计算^[15]：

(7)${\rm{SNR}} \propto \int_{{V_{{\rm{sample}}}}} {\frac{{{{B_0^2 \cdot {B_1}} \mathord{\left/ {\vphantom {{B_0^2 \cdot {B_1}} i}} \right. } i}}}{{\sqrt {\Delta f} \cdot \sqrt R }}{\rm{d}}V} $

其中，${V_{{\rm{sample}}}}$是有效的激励区域体积，R是线圈输入电阻，${B_1}/i$是线圈灵敏度.射频线圈带宽$\Delta f = {{{f_0}} \mathord{\left/ {\vphantom {{{f_0}} Q}} \right. } Q} = {{{R_{{\rm{ac}}}}} \mathord{\left/ {\vphantom {{{R_{{\rm{ac}}}}} {2{\rm{ \mathsf{ π} }}L}}} \right. } {2{\rm{ \mathsf{ π} }}L}}$，${R_{{\rm{ac}}}}$为线圈等效电阻，L为线圈等效电感，${f_0}$为磁共振中心频率，Q表示线圈的品质因数.在恒定磁场梯度和在该带宽情况下，样品的受激励区域厚度${d_{{\rm{sample}}}} = {{\Delta f} \mathord{\left/ {\vphantom {{\Delta f} G}} \right. } G} = {{{R_{{\rm{ac}}}}} \mathord{\left/ {\vphantom {{{R_{{\rm{ac}}}}} {2{\rm{ \mathsf{ π} }}LG}}} \right. } {2{\rm{ \mathsf{ π} }}LG}}$，G为目标区域内恒定磁场梯度，中心频率${f_0}$对应的位置在半径${r_0}$的圆上，则激励区域体积${V_{{\rm{sample}}}} = {d_{{\rm{sample}}}} \cdot 2{\rm{ \mathsf{ π} }}{r_0} = {{{R_{{\rm{ac}}}}{r_0}} \mathord{\left/ {\vphantom {{{R_{{\rm{ac}}}}{r_0}} {LG}}} \right. } {LG}}$.

建立非线性规划模型：

(8)$\begin{gathered} \max {\rm{SNR = }}\int_{{V_{{\rm{sample}}}}} {\frac{{B_0^2 \cdot {B_1} \cdot \sqrt {2{\rm{ \mathsf{ π} }}L} }}{{{R_{{\rm{ac}}}}}}{\rm{d}}V} \\ s.t. \left\{ \begin{gathered} 0.4 \times {10^{ - 3}} \leqslant w \leqslant 0.8 \times {10^{ - 3}} \\ w + 0.1 \times {10^{ - 3}} \leqslant d \leqslant 2 \times {10^{ - 3}} \\ 5 \times {10^{ - 3}} \leqslant {L_d} \leqslant 60 \times {10^{ - 3}} \\ \end{gathered} \right. \\ \end{gathered} $

其中，B₀表示主磁体在目标区域内产生的磁场，B₁表示射频线圈在目标区内产生的磁场与B₀正交的分量.w为导线宽度，${L_d}$为单个线圈的平均弧长，d为相邻导线之间的距离，单位均为m.

每个结构参数的线圈相对信噪比曲线如图 5所示，相对信噪比根据(8)式计算得到. 经过优化得到最佳结构：圆周上均匀分布4个线圈，每个线圈6匝；射频线圈自身结构的最优参数为：平均弧长L_d=15.5×10^-3 m，导线宽度w = 0.7×10^-3 m，线间距d=0.8×10^-3 m.

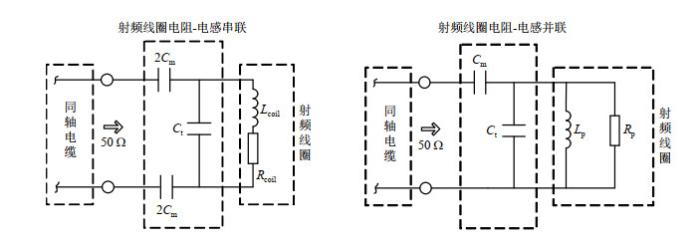
为减小能量的反射，从而实现能量传输效率的最大化，需要使射频线圈在共振频率下的阻抗接近传输线阻抗（50 Ω），因此需要对射频线圈进行调谐匹配.初始匹配电路如图 6左图所示，在共振频率点，射频线圈的电阻为${R_{{\rm{coil}}}}$，电感为${L_{{\rm{coil}}}}$.通过改变匹配电容${C_{\rm{m}}}$和调谐电容${C_{\rm{t}}}$，使得输入端的谐振频率为磁共振频率，输入阻抗为50 Ω.

为了便于分析，将线圈等效电路进行并联转换（图 6右图），其中L_p为并联结构等效线圈电感，R_p为并联结构的等效线圈电阻，其与串联结构的等效线圈参数的关系可以表示为：

(9)$\begin{array}{*{20}{c}} {{R_{\rm{p}}} = ({Q^2} + 1){R_{{\rm{coil}}}}} \\ {{L_{\rm{p}}} = \frac{{{L_{{\rm{coil}}}}(1 + {Q^2})}}{{{Q^2}}}} \end{array}$

对于射频线圈而言，将射频线圈的电抗值与交流电阻值之比定义为Q值：

(10)$Q = \frac{{2{\rm{ \mathsf{ π} }}f{L_{{\rm{coil}}}}}}{{{R_{{\rm{coil}}}}}}$

f为射频线圈的工作频率.通过改变${R_p}$，即可改变Q值；降低Q值，可提高线圈的带宽.对于本文所设计的梯度磁场，为减小Q值，提高信噪比，仅需减小${R_p}$即可，本文选择并联方式.在实际电路中，根据初步的估算并联电阻${R_p}$约为几千欧姆.

测量时，采用CPMG信号来评估传感器的信噪比，信噪比表示为：

(11)${\rm{SNR}} = \frac{{{A_{{\rm{signal}}}}}}{{{A_{{\rm{noise}}}}}}$

其中，${A_{{\rm{signal}}}}$为CPMG信号前20个点的平均值，${A_{{\rm{noise}}}}$为CPMG信号后20个点的平均值.

对1~14 kΩ范围的并联电阻进行了实验，测量样品为水饱和的石英砂样品，采用CPMG序列，采样参数为：射频脉冲频率2.526 MHz，脉冲宽度6.5 μs，回波时间为120 μs，重复时间为200 ms，回波个数为12 000，90˚脉冲幅值-20dB(@500W)，180˚脉冲幅值-14dB(@500W)）.根据并联电阻与由(11)式计算得到的信噪比关系（图 7），得知最佳的并联电阻为6.2 kΩ.该电阻值下的信噪比为65，相对于不并联电阻（信噪比为46），提高了41.3%.

本文选择两种颗粒尺寸的干燥沙子加水制成模型土壤样品（图 8）：一种为尺寸较小的沙土（直径约0.25 mm，样品A），另一种为尺寸较大的石英砂（直径约0.85~2.00 mm，样品B）.传感器测量区域为环状区域，本文以该区域的水分含量评估整个样品的水分含量.

样品A中沙土和水的初始重量分别为181.075 g和38.538 g，样品B中石英砂和水初始重量分别为216.367 g和62.004 g.本文获得不同水分含量的土壤样品的方式为恒温干燥，在干燥过程中每隔2 h测量一次.

称重法测量样品水分含量表示为^[16]：

(12)$\eta = \frac{{{m_1} - {m_2}}}{{{m_1}}} \times 100\% $

其中，${m_1}$为样品总重量，${m_2}$为样品中初始的干燥沙土或石英砂的重量.

用CPMG方法（图 9）根据土壤样品中水分的T₂分布测量水分含量时，CPMG信号峰值可以表述成m个指数函数的和^[17]

(13)$y(t) = \sum\limits_{j = 1}^m {f({T_{2j}}){{\rm{e}}^{ - t/{T_{2j}}}} + \xi (t)} $

其中，$y(t)$为测量的信号幅值，$\xi (t)$为噪声信号，${T_{2j}}$表示第j个组分对应的横向弛豫时间，$f({T_{2j}})$表示横向弛豫时间为${T_{2j}}$的分量对应的信号幅值.求解上述方程组可得$f({T_2})$，将$f({T_2})$函数中每个峰包围的面积按下式计算：

(14)${A_{{\rm{peak}}}} = \int_{{T_{2\min }}}^{{T_{2\max }}} {f({T_2})\text{d}{T_2}} $

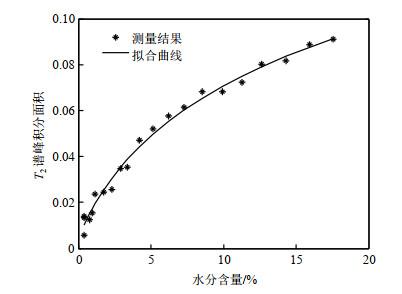
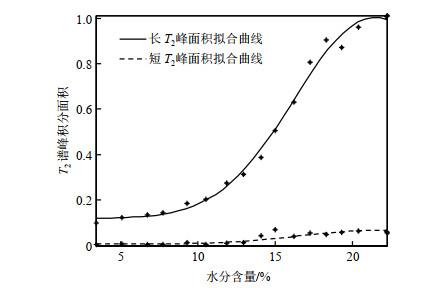
两种样品的T₂谱峰面积与称重法获得的样品含水量的关系分别如图 10和图 11所示.图 10与图 11结果显示，模型土壤的含水量与T₂谱峰的积分面积正相关，不同的地方在于沙土样品（图 10）的谱峰面积随着水分含量的降低而减小，并且减小速率逐渐增大；而石英砂样品（图 11）的谱峰面积随着水分含量降低的减小速率是先较小，后增大，然后再减小.主要原因可能是含水量较丰富时，沙土样品中的水分以沙土颗粒周围的束缚水为主，而石英砂样品中的水分以颗粒中间的自由水为主.图 11中，长T₂表示的分量性质趋近于孔隙中间的自由水，短T₂表示的分量趋近于孔隙周围的束缚水.随着水分含量的减少，首先是自由水含量先快速减少，然后是孔隙周围的束缚水减少，由于该样品中自由水含量远远大于束缚水含量，因此样品含水量减少的过程中，束缚水含量的变化较自由水慢.而对于图 10所示，由于孔隙尺寸已经足够小，通过T₂谱已经很难区分孔隙中的自由水和束缚水了.因此，要更进一步区分孔隙问题，则应该引入扩散系数这一物理量，对自扩散系数和T₂分布同时进行分析，也是本文设计恒定梯度磁场传感器的初衷，将在后续工作中详细阐述.

农业生产和生态环境保护中，土壤水分是一个十分重要的参考量，对于水源的充分利用和保障作物的生长至关重要.本文从小型化、轻量化、现场化的测量目标着手，设计了Inside-out NMR传感器，考虑到传感器恒定梯度的特性，通过非线性优化对传感器磁体结构和射频线圈结构进行了优化，并在射频线圈的阻抗匹配中采用宽频带匹配方法，通过降低品质因素，增加传感器能够激励的带宽，从而增加样品的激励区域，提高了传感器的整体信噪比，在不并联电阻的基础上提高了41.3%.小颗粒沙土和大颗粒石英砂土壤模型样品的T₂谱峰面积与称重法获得的含水量的相关性分析初步验证了该传感器用于测量土壤水分的可行性.