波谱学杂志, 2021, 38(2): 249-254 doi: 10.11938/cjmr20202866

研究简报

一种基于非标准矩形微波腔的铷频标腔泡系统

李菡1,2, 康松柏1, 王鹏飞1, 赵峰,1

1. 中国科学院原子频标重点实验室(中国科学院精密测量科学与技术创新研究院), 湖北 武汉 430071

2. 中国科学院大学, 北京 100049

A Cavity-cell Assembly of Rubidium Frequency Standard Based on a Non-standard Rectangular Microwave Cavity

LI Han1,2, KANG Song-bai1, WANG Peng-fei1, ZHAO Feng,1

1. CAS Key Laboratory of Atomic Frequency Standards (Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences), Wuhan 430071, China

2. University of Chinese Academy of Sciences, Beijing 100049, China

通讯作者:

赵峰, Tel: 13476142303, E-mail: zf_lucky@apm.ac.cn

ZHAO Feng, Tel: 13476142303, E-mail: zf_lucky@apm.ac.cn


收稿日期: 2020-10-14  

基金资助: 创建国家科技创新平台项目资助.  2018011005132289

Received: 2020-10-14  

摘要

针对超薄型铷频标应用需求，本文研制了一种基于开槽管腔原理的非标准矩形微波腔.它的厚度仅为12 mm，仿真结果显示其微波场方向因子约为0.9.测量了基于该微波腔设计的腔泡系统的87Rb原子双共振跃迁信号，并通过外推法得到铷原子吸收泡内双共振谱线的本征线宽约为452 Hz.在优化后的实验参数下，该腔泡系统散弹噪声对铷频标短期频率稳定度的限制可达到5.2×10-13τ-1/2.

关键词： 铷频标 ; 非标准矩形微波腔 ; 频率稳定度 ; 腔泡系统

Abstract

To meet the requirement of ultra-thin rubidium frequency standard, we developed a non-standard rectangular cavity based on the slotted-tube microwave cavity with 12 mm thickness and a field orientation factor of about 0.9. The data set of 87Rb double-resonance signals of the cavity-cell assembly was measured. The results showed that the intrinsic linewidth is about 452 Hz. With the optimized experimental parameters, the cavity-cell assembly has a potential short-term stability of 5.2×10-13τ-1/2 limited by the shot noise.

Keywords： rubidium frequency standard ; non-standard rectangular microwave cavity ; frequency stability ; cavity-cell assembly

PDF (727KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

李菡, 康松柏, 王鹏飞, 赵峰. 一种基于非标准矩形微波腔的铷频标腔泡系统. 波谱学杂志[J], 2021, 38(2): 249-254 doi:10.11938/cjmr20202866

LI Han. A Cavity-cell Assembly of Rubidium Frequency Standard Based on a Non-standard Rectangular Microwave Cavity. Chinese Journal of Magnetic Resonance[J], 2021, 38(2): 249-254 doi:10.11938/cjmr20202866

引言

铷频标因体积小、重量轻、可靠性强、性能较高等优势广泛应用于航空航天、导航、通信、电力等领域[1].尤其是随着小型化、低功耗铷频标技术的发展，铷频标在越来越多的应用中逐步取代传统高稳晶体振荡器，具有广阔的应用前景[2].其中，超薄型铷频标在移动通信、无人机、军用装备等方面有着较大的应用需求.目前超薄型铷频标主要有Microsemi公司的SA.22c型[3]和航天科工203所BM2102-05型[4]，整机厚度分别约为23.8 mm和19 mm.

铷频标整机系统主要包括物理系统与电路系统.其中，物理系统是铷频标的核心，是制约铷频标整机厚度和频率稳定度的主要因素，而物理系统的关键是微波腔.当前超薄型铷频标通常采用减小微波腔的厚度来实现，主要有两种方案：一是采用小型圆柱形磁控管腔[5]，二是采用非标准矩形同轴横电磁波（transverse electromagnetic modes，TEM）微波腔[6].本实验室综合了非标准矩形微波腔与开槽管腔[7]的原理，研制了一种体积为5.4 mL且厚度仅为12 mm的非标准矩形微波腔，其场分布模式能有效提高腔泡内87Rb原子的微波跃迁效率，预期可制成整机厚度小于20 mm的超薄型铷频标.

本文选用激光作为泵浦光对基于此非标准矩形微波腔的腔泡系统的性能潜力进行了测量与评估.相较于谱灯泵浦，激光泵浦方案能让我们直接获得钟跃迁谱线，从而实现对腔泡系统的原子双共振谱线本征线宽的准确评估.此外，对于将来研制高性能的超薄型激光泵浦铷频标有指导意义.

1 非标准矩形微波腔的结构和场分布

1.1 微波腔及腔泡系统结构

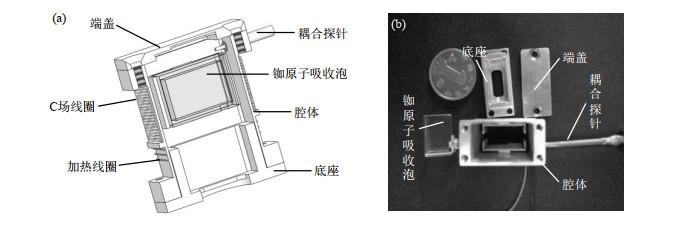
本实验室研制的非标准矩形微波腔尺寸为25.2 mm×18 mm×12 mm.该腔由端盖、腔体和底座构成，如图 1(a)所示.端盖从上端将腔体封闭，底座带有通光孔，从腔体下端插入腔体内部.腔体是一个横截面为“回”字形的金属筒，外侧缠绕C场线圈和加热线圈，分别用来提供静磁场和腔体控温.腔体内部是对称分布的两个U形金属极片，两个极片端面之间构成两个窄槽，类似于开槽管腔，U形极片和金属筒内壁由脊状金属结构连接.U形极片围成的区域内安装长方体状铷原子吸收泡，内部除充有87Rb原子外，还充有缓冲气体（Ar、N2）用来压窄钟跃迁谱线线宽.位于腔体上端侧壁的耦合探针将微波信号馈入物理系统，激励87Rb原子产生钟跃迁信号.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   基于非标准矩形微波腔的腔泡系统结构. (a)剖面图；(b)腔泡系统实物图

Fig.1   Structure of the cavity-cell assembly based on the non-standard rectangular microwave cavity. (a) Cross section; (b) Photos of cavity-cell assembly


1.2 微波场分布

激励铷频标产生钟跃迁信号需要平行于量子化轴（C场方向）的微波磁分量，且微波场磁力线沿量子化轴方向分布越密，87Rb原子微波跃迁效率越高，即跃迁信号越强.使用方向因子[8]描述微波磁分量偏振方向与量子化轴的平行程度，其含义是铷原子吸收泡内微波磁场的轴向（C场方向）分量场强度与总强度之比.该腔泡系统的场分布仿真结果如图 2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   非标准矩形微波腔微波场分布仿真

Fig.2   Simulation of microwave field distribution in the non-standard rectangular microwave cavity


磁力线颜色深浅表示磁场强弱，磁力线的箭头表示磁场方向.虚线框处为吸收泡放置处，此处磁力线沿量子化轴分布密集且高度平行，即该区域内微波场激励87Rb原子跃迁的效率最高.仿真结果显示该非标准矩形微波腔的场方向因子达到0.9，与Stefanucci等[9]的研制的高性能微波腔的方向因子相当.

2 原子双共振谱线线宽与鉴频曲线

2.1 腔泡系统双共振谱线线宽测量

气泡型铷频标的光-微波双共振谱线为洛伦兹线型，其谱线展宽主要来自碰撞展宽（本征线宽）、微波功率展宽以及泵浦光功率展宽.根据文献[10]，该线宽近似为：

$\Delta \nu = \frac{1}{\pi }({\gamma _2} + \frac{{{\mathit{\Gamma } _p}}}{2})\sqrt {S + 1} $

${\gamma _2}$为横向弛豫率，与本征线宽呈正比；${\mathit{\Gamma } _p}$为泵浦速率，与泵浦光功率呈正比，在本实验中用背景光电流表征；S为微波饱和因子，与微波功率呈正比.

测量腔泡系统双共振谱线的实验装置如图 3所示.将铷原子吸收泡温度控制在343 K，再使用波长为780 nm（87Rb原子的D2，a线，如图 4所示）、线宽约为100 kHz激光泵浦泡中的87Rb原子，实现$|F = 2, {m_F} = 0 > $与$|F = 1, {m_F} = 0 > $能级间粒子数反转，同时将频率为6.834 GHz的微波信号通过耦合探针馈入到非标准矩形微波腔内，激励87Rb原子发生双共振跃迁.跃迁信号加载在透过铷原子吸收泡的泵浦光中，由光电池接收变为微弱的电流信号后，传递至放大器放大并转换为易采集的电压信号.通过扫描馈入非标准矩形微波腔的微波频率在示波器上采集相应的双共振谱线，对该谱线进行拟合可得到线宽.

图3

新窗口打开| 下载原图ZIP| 生成PPT

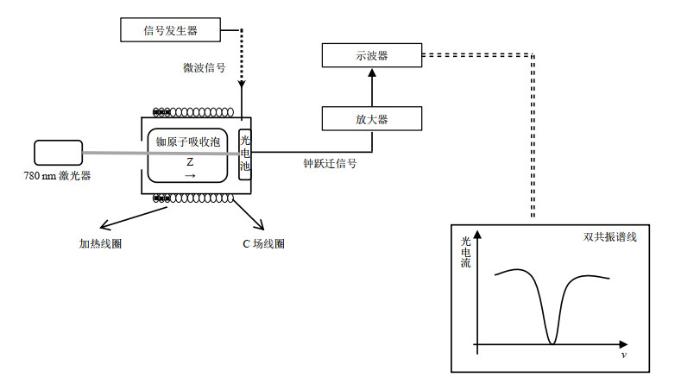
图3   测量腔泡系统双共振谱线的实验装置

Fig.3   Experiment setup for measuring double-resonance signal of the cavity-cell assembly


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   87Rb原子能级跃迁图

Fig.4   Energy levels and transitions of 87Rb


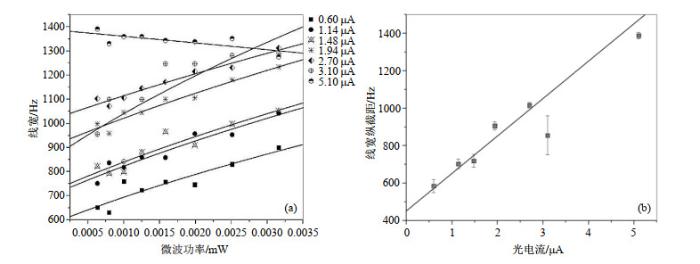
本征线宽是原子双共振谱线的一个重要参数，对铷频标设计具有重要的指导意义.为得到原子双共振谱线的本征线宽，需要消除微波功率展宽和泵浦光功率展宽的影响，为此我们进行了如下实验：首先在相同背景光电流的条件下，测量并记录一组线宽随微波功率变化的数据，然后根据(1)式对这组数据以微波功率为自变量进行拟合得到纵截距，则该纵截距是仅存在本征线宽和光功率展宽的线宽.然后调整背景光电流的数值并重复上述实验操作，得到一组不同光电流值对应的纵截距.将这一组纵截距以背景光电流为自变量进行拟合，外推[11]得到背景光电流为0时的线宽即为本征线宽.实验中，微波功率从0.003 16 mW步径减小至0.000 6 mW，背景光电流值从0.6 μA步径增加至5.1 μA.

图 5(a)中每个数据点对应为不同背景光电流和微波功率下测量得到的谱线线宽.使用图案种类区分背景光电流值，横轴表示微波功率，纵轴表示线宽；每条拟合线描述了在背景光电流相同时线宽随微波功率的变化，并可推算出纵截距（即微波功率为0时）的谱线线宽.图 5(a)中不同背景光电流对应的纵截距示于图 5(b)，对其作线性拟合、外推得到原子双共振跃迁谱线本征线宽值为452 Hz，误差值为22 Hz.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   (a) 不同微波功率和背景光电流条件下的线宽变化；(b)线宽纵截距随背景光电流的变化

Fig.5   (a) Variation of linewidths under different microwave powers and background light currents; (b) Linewidths without microwave power broadening as a function of background light current


2.2 鉴频曲线的测量

鉴频曲线是腔泡系统的特征曲线，其鉴频斜率和双共振谱线的背景噪声决定了基于该腔泡系统的铷频标短期频率稳定度的极限$\sigma (\tau )$，具体可用下式描述[12].

$\sigma (\tau ) = \frac{N}{{\sqrt 2 {K_D}{f_0}}}{\tau ^{ - 1/2}}$

N是噪声功率谱密度；${K_D}$是鉴频曲线的斜率；${f_0}$是钟跃迁频率，为6.834 GHz；τ是采样时间.

经过参数优化，背景光电流为2.78 μA、微波功率为0.003 mW时，腔泡系统对铷频标短期频率稳定度的限制最小.此时双共振谱线如图 6(a)所示，该谱线的对比度（即信号幅值△I和背景光电流I之比）大约为12%，线宽约为1 222 Hz.利用调制-解调方法[13]获得图 6(b)中的鉴频曲线，其鉴频斜率${K_D}$为0.18 nA/Hz.

图6

新窗口打开| 下载原图ZIP| 生成PPT

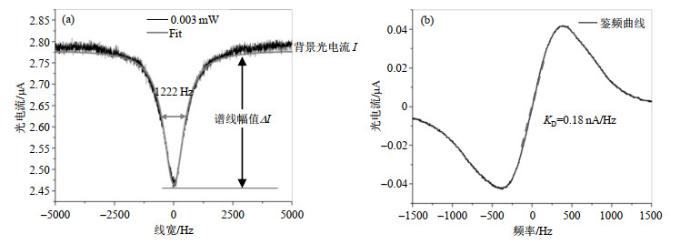
图6   (a) 腔泡系统的双共振谱线；(b)鉴频曲线

Fig.6   (a) Double-resonance signal of the cavity-cell assembly; (b) Frequency discrimination curve


如果仅考虑背景光电流的散弹噪声，其噪声功率谱密度可表示为$N = \sqrt {{\rm{2}}e{I_0}} $，e是电荷电量，${I_0}$是双共振谱线半高宽处的光电流值（2.62 μA）.根据(2)式计算出该物理系统的散弹噪声对铷频标短期频率稳定度限制可达到仅5.2×10-13τ-1/2.

3 结论

我们研制了一种可用于铷频标的非标准矩形微波腔，厚度仅为12 mm.该微波腔具有非常优越的场模式，仿真结果显示其场方向因子可达到0.9.另外，对基于该非标准矩形微波腔的腔泡系统的本征线宽进行了测量，结果显示腔内铷原子吸收泡的本征线宽约为452 Hz.最后，在优化后的实验条件下，对该腔泡系统的性能进行了评估，结果显示该腔泡系统的散弹噪声对铷频标短期频率稳定度的限制可达到5.2×10-13τ-1/2，在将来有可能实现高性能铷频标的应用.

利益冲突【-逻*辑*与-】#160;【-逻*辑*与-】#160;无

参考文献

BANI T , AFFOLDERBACH C , CALOSSO C E , et al.

High-performance laser-pumped rubidium frequency standard for satellite navigation

[J]. Electro Lett, 2011, 47 (12): 698- 699.

DOI:10.1049/el.2011.0389      [本文引用: 1]

JI Y , SHANG J T , LI G L , et al.

Microfabricated shaped rubidium vapor cell for miniaturized atomic magnetometers

[J]. IEEE Sensors Letters, 2020, 4 (2): 1- 4.

URL     [本文引用: 1]

MICROCHI: Microsemi_SA22c_Datasheet[OL]. https://www.microsemi.com/product-directory/embedded-clocks-frequency-references/3961-sa-22c#resources

[本文引用: 1]

国际技术转移中心: 航天科工"卡片铷钟"实现量产[OL]. [2018-11-17]. https://www.kphzcittc.com/demander.html?article_id=152.

[本文引用: 1]

YANG S Y , LIANG Y T , TU J H , et al.

Investigation on magnetron cavity used in rubidium atomic frequency standards

[J]. Chinese Journal of Quantum Electronics, 2012, 29 (4): 400- 405.

DOI:10.3969/j.issn.1007-5461.2012.04.003      [本文引用: 1]

杨世宇, 梁耀廷, 涂建辉, 等.

用于铷原子频标的磁控管腔研究(英文)

[J]. 量子电子学报, 2012, 29 (4): 400- 405.

DOI:10.3969/j.issn.1007-5461.2012.04.003      [本文引用: 1]

DENG J. Subminiature microwave cavity, its synthesis and use: U.S. Patent 6133800[P]. 2000-10-17.

[本文引用: 1]

ZHONG D, XIA B H, AN S F, et al. Investigation on physics package with slotted-tube microwave cavity for rubidium atomic frequency standard[C]//2009 IEEE International Frequency Control Symposium Joint with the 22nd European Frequency and Time forum, Pisa, Italy. USA: IEEE, 2009: 1019-1022.

[本文引用: 1]

MEHDIZADEH M , ISHII T K , HYDE J S , et al.

Loop-gap resonator: A lumped mode microwave resonant structure

[J]. IEEE T Microw Theory, 1983, 31 (12): 1059- 1064.

DOI:10.1109/TMTT.1983.1131661      [本文引用: 1]

STEFANUCCI C , BANI T , MERLI F , et al.

Compact microwave cavity for high performance rubidium frequency standards

[J]. Rev Sci Instrum, 2012, 83 (10): 104706.

DOI:10.1063/1.4759023      [本文引用: 1]

VANIER J , AUDOIN C . The quantum physics of atomic frequency standards[M]. Florida: CRC Press, 1989.

[本文引用: 1]

SIDI A . Practical extrapolation methods: Theory and applications[M]. England: Cambridge university press, 2003.

[本文引用: 1]

BANDI T , AFFOLDERBACH C , STEFANUCCI C , et al.

Compact high-performance continuous-wave double-resonance rubidium standard with 1.4x10-13t-1/2stability

[J]. IEEE T Ultrason Ferr, 2014, 61 (11): 1769- 1778.

DOI:10.1109/TUFFC.2013.005955      [本文引用: 1]

王义遒. 量子频标原理[M]. 北京: 科学出版社, 1986.

[本文引用: 1]

/

〈 〉

网站设计版权所有 © 2017 《波谱学杂志》编辑部
地址：湖北省武汉市武昌区小洪山西30号 中科院精密测量科学与技术创新研究院波谱楼 《波谱学杂志》编辑部
邮编：430071　电话/传真：(086)027－87198791   E-mail: magres@wipm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发