引言
核磁共振(NMR)技术主要包括NMR波谱和磁共振成像(MRI),其作为一种有效的检测手段,在石油探测[1]、食品分析[2, 3]、药品鉴定[4]、医疗诊断[5, 6]等不同领域都具有广泛的应用.NMR波谱是分子中原子核自旋能级的跃迁产生的吸收光谱,是分析物质微观化学结构、构象和弛豫现象的有效手段之一.在弛豫现象发生的过程中,磁化矢量逐渐由非平衡态恢复到外磁场作用下的热平衡状态,同时发生着自旋-晶格弛豫(T1)和自旋-自旋弛豫(T2)[7].T1主要由核自旋和晶格间发生能量交换的方式来决定.液体体系中,在外加磁场作用下的核自旋,其T1往往远大于T2.在实验操作过程中,为保证施加射频脉冲期间,目标原子核自旋状态不受T2弛豫影响,因此,实际施加脉冲的时间应远小于目标原子核自旋的T1时间.基于这一原因,对于某些弛豫时间很短的核自旋体系,NMR技术的应用往往存在着一定的局限性.
长寿命核自旋单重态[8]作为一种特殊的量子态,由于具有自旋对称性,不受偶极-偶极相互作用的影响,因此通常具有较长的弛豫时间[9, 10].一般情况下,分子结构中某一位点核自旋单重态的寿命(Ts)会明显长于其T1.基于这一特性,核自旋单重态能有效解决一些研究对象因常规弛豫时间过短而难以进行NMR观测的问题,因而在磁共振检测领域具有重要的应用价值和广阔的应用前景[8].自被发现以来,国内外许多研究者对于核自旋单重态这一特殊状态及相关应用开展了一系列研究[11],多项研究表明其存在于多种二自旋[12]和多自旋体系[13]的分子中.早期研究[12, 14]显示,分子内含有的核自旋数量越多,核自旋单重态产生的条件就越苛刻,同时实验上制备单重态的难度也更高.而分子结构中孤立耦合体系的单重态制备效率高于非孤立体系[15, 16].目前,1H、13C和15N核是长寿命核自旋单重态研究中最常见的三种研究对象.在合适的物理条件下,通过设计脉冲序列,1H核的核自旋单重态的Ts相比T1,可提高数十倍,达到约10 min [17];15N核的核自旋单重态的Ts能达到25 min以上[14];而13C核的核自旋单重态的Ts能够超过1 h[12].除Ts较长外,核自旋单重态也不受梯度场脉冲的影响[12],因此在混合体系成分分析[18]、分子运动[19]、MRI[20]等领域都具有巨大的应用潜力.但是目前,对于不同分子单重态的制备与研究,仍处于初步的认知阶段.
单重态的制备受到多种因素的影响,包括自旋体系内相关原子的J耦合值、化学位移、制备的脉冲序列等.其中,脉冲序列的影响非常重要.基于不同脉冲的作用原理,在相似自旋体系内实现单重态的制备可以采取不同的脉冲序列组合.SLIC脉冲[9]常用于制备强耦合二自旋体系的单重态,本课题组在以往的研究[21]中利用SLIC脉冲成功制备了二自旋体系的单重态;M2S脉冲可用于制备同核二自旋系统,例如甘氨酸(Gly)中二自旋体系的单重态[9];本文作者所在课题组利用了基于不同原理的优化脉冲序列(OC)[22],在多种自旋体系内成功获得了1H核的单重态;绝热通道自旋顺序转换(APSOC)脉冲[23]可用于制备双自旋强耦合体系和弱耦合体系的单重态,并且制备效率较高,但是该脉冲为双通道实验,实验过程复杂,并且脉冲施加时间长;另外,还有一些脉冲序列可用于二自旋[11]或多自旋[24]的弱耦合体系的单重态制备.但是目前,对于脉冲序列影响单重态制备的规律,及其与其他因素之间的关系尚缺乏明晰统一的认识,而正确认识这些规律和关系,对进一步理解核自旋单重态的内在机理、拓展其应用领域,具有至关重要的意义.
本文以三肽分子AGG(Ala-Gly-Gly)的氘水溶液为研究对象,针对其中一组核自旋体系,首先分别使用SLIC、M2S和OC三种脉冲序列,制备了体系内两个1H核的核自旋单重态;然后测定了其Ts,并比较了三组脉冲制备核自旋单重态的效率;最后,我们进一步探究了脉冲序列影响1H核自旋单重态制备效率的机理.
1 理论部分
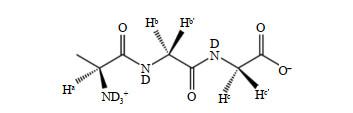
AGG分子中包含Hb、Hb'和Hc、Hc'两组二自旋体系(图 1).经理论计算,这两组自旋体系中的1H核,均可在一定条件下成功制备核自旋单重态.本文以Hc、Hc'二自旋体系为研究对象,分别将SLIC、M2S和OC三种脉冲序列用于制备核自旋单重态,并通过实验验证了其可行性.
图1
1.1 制备选定体系核自旋单重态的三组脉冲序列
图 2所示是制备AGG分子中选定二自旋体系的核自旋单重态的三种脉冲序列.
图2
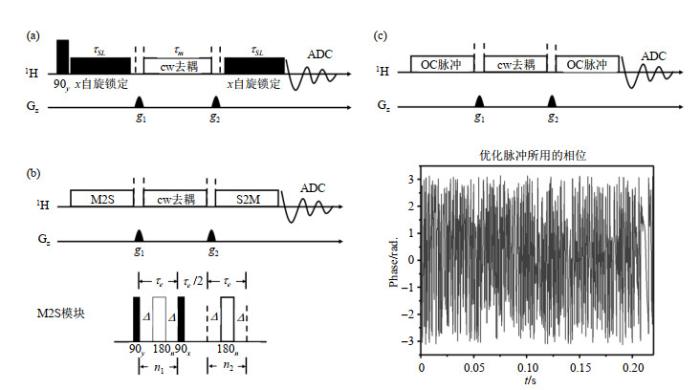
图2
针对AGG中的二自旋Hc、Hc'制备单重态的(a) SLIC脉冲序列[9];(b) M2S脉冲序列[9];(c) OC脉冲序列[22],优化脉冲的相位也绘制在脉冲序列方案下方
Fig.2
Pulse sequences of (a) SLIC[9], (b) M2S[9], and (c) OC pulse sequence[22] used for preparing nuclear singlet states in two spin systems of selected Hc, Hc' in AGG. The phase of optimal control pulse sequence is also plotted below the pulse sequence scheme
SLIC脉冲常用于制备强耦合二自旋体系的单重态,完整的脉冲施加过程图 2(a)所示:先在y方向上施加一个90°的硬脉冲;然后在x方向上施加时间为
M2S技术可用于研究同核二自旋系统和近等效异核系统,这种技术基于缓慢切换自旋锁定激发场来实现横向磁化强度和单重态之间互相高效地转化.M2S序列能够将磁化强度转化为单重态,而S2M序列则能够将单重态转化为可观测的横向磁化强度.基于M2S技术的脉冲序列的完整施加过程如图 2(b)所示:先施加一组M2S组合脉冲,然后施加梯度场
这里
这里幺正变换
这里∈为幅度改变的大小,
根据以上三种脉冲的形式可知:M2S主要包含多个延时与180°硬脉冲组成的片段,这些片段的个数以及每个片段内的延时需要进行优化;SLIC脉冲主要包含一个低功率的自旋锁定脉冲,其锁定的时间决定了脉冲的转化效率;而OC脉冲并没有固定的形式,其单个脉冲单元的幅度和相位都是可变的.
1.2 使用三组脉冲序列制备核自旋单重态效率的理论模拟
在分别施加三种核自旋单重态制备脉冲之前,当待测样品置于磁场中时,AGG分子中选定的二自旋体系Hc、Hc'处于热平衡状态:
理论上转变为的目标态为:
在实际SLIC脉冲的作用下,经过一系列演化后,体系的状态最终变为:
在用MATLAB进行理论模拟时,我们先将SLIC脉冲用MATLAB软件构造出来,以刘维尔方程的形式逐渐施加到热平衡态
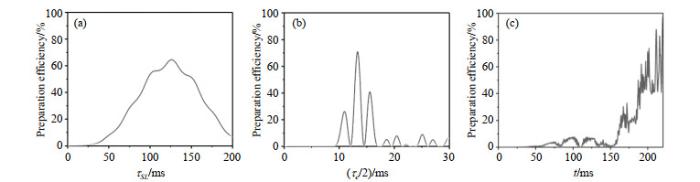
模拟计算结果如图 3(a)所示,当SLIC脉冲中自旋锁定部分的时间
图3
图3
MATLAB理论模拟得到的(a)使用SLIC序列制备核自旋单重态的理论效率与τSL的关系;(b)使用M2S序列制备核自旋单重态的理论效率与τe/2的关系;(c)使用优化序列制备核自旋单重态的理论效率与脉冲时间t的关系
Fig.3
(a) The relationship between the theoretical singlet preparation efficiency and τSL simulated by MATLAB using SLIC pulse sequence; (b) The relationship between the theoretical singlet preparation efficiency and τe/2 simulated by MATLAB using M2S pulse sequence; (c)The relationship between the theoretical singlet preparation efficiency and pulse time t simulated by MATLAB using the optimal control pulse sequence
在实际M2S脉冲的作用下,AGG分子中的二自旋体系经过相应演化后,体系的最终状态变为:
同样用MATLAB软件进行理论模拟,不断改变M2S脉冲中M2S模块部分的时间
模拟计算结果如图 3(b)所示,当M2S脉冲中M2S模块部分的时间
在实际OC脉冲的作用下,经过类似的演化后,最终体系的状态变为:
我们利用MATLAB计算了一次施加各个OC脉冲单元后核自旋的状态演化图,获得了OC脉冲理论制备效率随脉冲单元变化的趋势.不断改变OC脉冲时间t(0~220 ms),获得终态算符
模拟计算结果如图 3(c)所示,当OC脉冲时间t为220 ms时,单重态的理论转化效率达到最大,为97.12%.
理论模拟计算结果不仅证明使用上述三种脉冲序列都能够实现AGG分子中二自旋体系Hc、Hc'的单重态制备,还有利于初步确定实验的相关参数;同时,通过理论模拟计算得到,对于同一目标体系内的1H核,由于不同脉冲序列作用机制的差异,引起体系中用于描述系统总能量的哈密顿量的演化过程不同,最终他们制备核自旋单重态的理论效率也会有所差异.另外,此处理论模拟的转化效率暂未考虑弛豫因素的影响以及单重态向单量子态转化引起的效率变化.本文中使用的三种脉冲序列的总时间均较长,在整个脉冲施加过程中,如果考虑到自旋弛豫的影响,实验制备效率与理论制备效率相比会有所降低;而单重态向单量子态转化后,理论制备效率的最高点也有可能会发生改变.
2 实验部分
2.1 仪器与试剂
仪器:AVANCE III 500型NMR波谱仪(Bruker)、Norell 5 mm高通量NMR样品管.
试剂:AGG三肽分子购于杰贝欧生物试剂有限公司,纯度为98%;D2O(CIL)购于青岛腾龙微波科技有限公司,纯度为99.9%.
配制浓度为4 mg/mL的AGG氘水溶液.
2.2 NMR实验
NMR实验均在Bruker AVANCE Ⅲ 500型NMR波谱仪上完成.
在测试温度为25 ℃时,用常规单脉冲序列得到AGG溶液的1H NMR谱图.并用反转恢复法测定AGG中Hc、Hc'的T1.
测试温度为25 ℃时,分别采用图 2所示的三种脉冲序列对AGG中的Hc、Hc'体系进行核自旋单重态的制备和观测.
在所有实验中,90°脉冲宽度设置为10 μs,循环等待时间(D1)为5 s,去耦功率等其他相关实验参数通过理论计算初步确定,并在实际实验操作中进行优化调整.
3 结果与讨论
3.1 使用三种脉冲制备二自旋体系Hc、Hc'的核自旋单重态的效率
针对AGG分子中的二自旋体系Hc、Hc',我们使用SLIC、M2S和OC脉冲这三组基于不同原理的单重态制备脉冲序列,都成功实现了对该体系1H核的单重态制备.另外,从1.2节理论计算不同脉冲序列制备核自旋单重态的效率可以看出,三组脉冲中施加脉冲的时间对单重态的制备效率影响较大.我们在随后的实验中,通过改变三组脉冲中的脉冲施加时间,进一步对制备效率进行了检测.
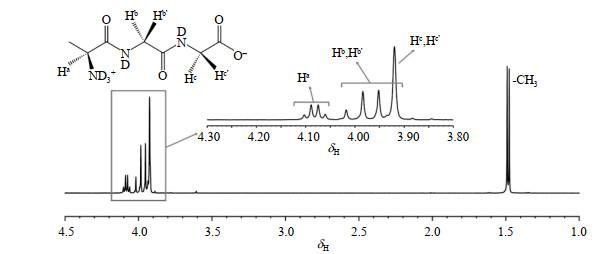
图 4为AGG氘水溶液使用常规单脉冲序列测得的1H NMR谱图,累加次数为1.我们对其谱峰进行了归属,因Hc、Hc'出峰位置相近,在1H NMR谱图中只显示为一个单峰,化学位移为δH 3.92.两个氢核属于强耦合体系,它们之间的化学位移差值及准确的J耦合值无法在谱图上进行直接读取,通过计算可获得两质子间的化学位移差值为5.6 Hz,J耦合为18.24 Hz.
图4
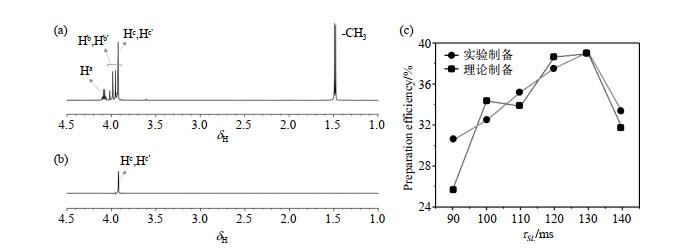
将射频中心O1定于Hc、Hc'的共振频率,约1 962 Hz处,施加SLIC脉冲序列,对Hc、Hc'自旋体系进行单重态制备并检测,实验结果如图 5(b)所示.在SLIC脉冲序列中梯度场脉冲的影响下,其他的非单重态信号被散相,基本消失,而Hc、Hc'的单重态不受外加梯度场的影响,得以保留.在本文中,我们定义单重态制备脉冲获得的Hc、Hc'信号的积分强度与1H NMR谱图中Hc、Hc'信号的积分强度的比值为单重态的制备效率.核自旋单重态的实验制备效率和理论制备效率与SLIC脉冲序列自旋锁定部分的时间
图5
图5
(a) AGG氘水溶液的1H NMR谱图;(b)用SLIC序列制备的AGG分子中Hc、Hc'单重态的NMR谱图;(c)使用SLIC脉冲得到AGG分子中Hc、Hc'单重态的实验制备效率(

Fig.5
(a) 1H NMR spectrum of AGG in deuterium water; (b) The NMR spectrum of nuclear spin singlet state of Hc, Hc' in AGG using SLIC pulse sequence; (c) The relationships of theoretical (

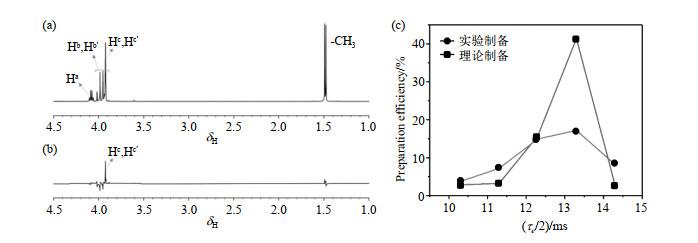
与SLIC方法类似,将射频中心O1定于约1 962 Hz处,施加M2S脉冲序列,得到的二自旋体系Hc、Hc'单重态的NMR谱图如图 6(b)所示.在M2S脉冲序列中梯度场脉冲的影响下,同样只有Hc、Hc'的单重态信号得以保留.核自旋单重态的实验制备效率和理论制备效率与M2S脉冲序列M2S模块部分的时间
图6
图6
(a) AGG氘水溶液的1H NMR谱图;(b)用M2S序列制备的AGG分子中Hc、Hc'单重态的NMR谱图;(c)使用M2S脉冲得到AGG分子中Hc、Hc'单重态的实验制备效率(

Fig.6
(a) 1H NMR spectrum of AGG in deuterium water; (b) The NMR spectrum of nuclear spin singlet state of Hc, Hc' in AGG using M2S pulse sequence; (c) The relationships of theoretical (

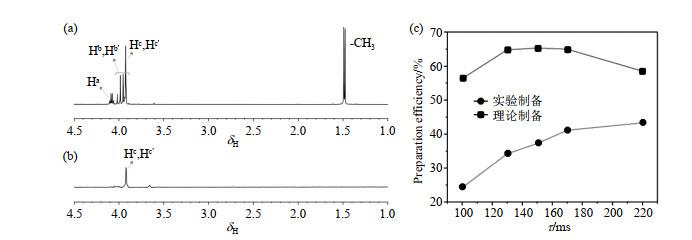
最后,我们对自旋体系Hc、Hc'施加OC脉冲,得到的二自旋体系Hc、Hc'单重态的NMR谱图如图 7(b)所示.在OC脉冲的作用下,与前两组实验结果类似,谱图中包含Hc、Hc'的单重态信号.核自旋单重态的实验制备效率和理论制备效率与所使用的不同OC脉冲的时间τ(取值为100、130、150、170和220 ms)的关系如图 7(c)所示:考虑弛豫作用后,最高理论制备效率对应的τ在170 ms附近;随着τ的增加,实验制备效率也逐渐增加,在我们设置的OC脉冲时间范围内,最高实验制备效率(约为43.3%)对应的τ为220 ms.我们认为这与OC脉冲的功率设置的准确性有一定的关系.另外,OC脉冲虽然在理论上能够实现状态的最大转化,但因为序列中的脉冲片段较多,实验上实现时会因为单个小脉冲的不准确而累计产生较大的误差,可能导致τ不同时,理论制备效率与实际制备效率偏差较大.
图7
图7
(a) AGG氘水溶液的1H NMR谱图;(b)用OC脉冲序列制备的AGG分子中Hc、Hc'单重态的NMR谱图;(c)使用OC脉冲得到AGG分子中Hc、Hc'单重态的实验制备效率(

Fig.7
(a) 1H NMR spectrum of AGG aqueous solution; (b) The NMR spectrum of nuclear spin singlet state of Hc, Hc' in AGG using OC pulse sequence; (c) The relationships of theoretical (

上述实验除考虑了单重态转化为单量子态后会引起最终检测时的效率变化外,由于AGG分子的T1较短,约为866 ms,而实验所用的三种脉冲序列的总时间(包括单重态的制备和观测)分别为:SLIC脉冲约262 ms,M2S脉冲452 ms,OC脉冲约440 ms.与分子本身的T1相比,脉冲时间较长,脉冲施加期间自旋弛豫不可忽略.在考虑弛豫的影响后,脉冲序列的理论制备效率会进一步下降.例如:考虑弛豫因素后,SLIC、M2S和OC脉冲的信号强度分别衰减为expSLIC(-262/866)≈0.739、expM2S(-452/866)≈0.594和expOC(-440/866)≈0.602.经折算后,在我们设定的时间范围内获得三种脉冲的最高理论制备效率分别约为38.9%、40.8%和65.3%.而且这三种脉冲的理论效率是通过对各自的脉冲时间进行优化后得到的,如果改变施加脉冲的时间,则其理论效率会发生变化,如图 5(c)、6(c)和7(c)中的方块折线.值得注意的是,图 7(c)中的折线展示的是不同的OC脉冲(时间不同,形状也不同)所制备的单重态的效率;而图 3(c)的曲线展示的是选定某一个OC脉冲后(此处为220 ms对应的OC脉冲形状),单重态的算符随脉冲的形状(即时间)的变化.因此图 7(c)中的方块折线不能直接从图 3(c)中截取.
3.2 二自旋体系Hc、Hc'的T1及三种脉冲作用下核自旋单重态的Ts
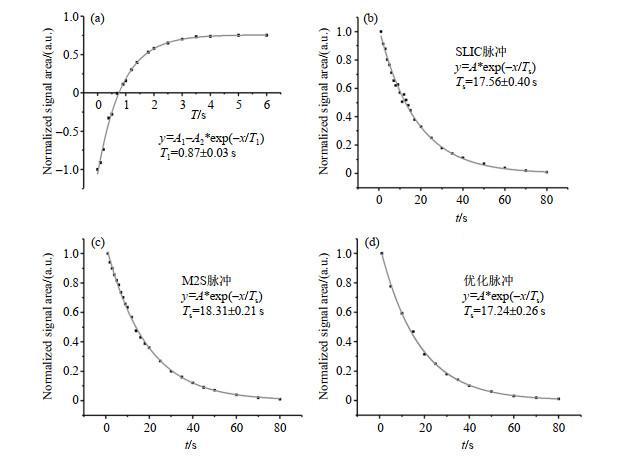
通过改变90°脉冲和180°脉冲之间的时间间隔T,我们利用反转恢复法测定了AGG分子中选定二自旋体系Hc、Hc'的T1.图 8(a)所示为Hc、Hc'的T1衰减曲线,通过反转恢复法测得的不同演化时间T(范围为0~6 s)时,对Hc、Hc'的积分面积进行归一化处理,实线为用公式y=A1-A2*exp(-x/T1)拟合得到的曲线,拟合得到目标自旋体系Hc、Hc'的T1为(0.87±0.03)s.
图8
图8
(a) AGG分子Hc、Hc'自旋体系的T1衰减曲线,T1=0.87±0.03 s;(b)利用SLIC脉冲获得的AGG分子Hc、Hc'单重态的Ts衰减曲线,Ts=17.56±0.40 s;(c)利用M2S脉冲获得的的AGG分子Hc、Hc'单重态的Ts衰减曲线,Ts=18.31±0.21 s;(d)利用OC脉冲获得的AGG分子Hc、Hc'单重态的Ts衰减曲线,Ts=17.24±0.26 s
Fig.8
(a) The T1 decay curve of Hc, Hc' in AGG, T1=0.87±0.03 s; (b) The Ts decay curve of Hc、Hc' singlet state in AGG using SLIC pulse sequence, Ts=17.56±0.40 s; (c) The Ts decay curve of Hc、Hc' singlet state in AGG using M2S pulse sequence, Ts=18.31±0.21 s; (d) The Ts decay curve of Hc, Hc' singlet state in AGG using OC pulse, Ts=17.24±0.26 s
核自旋单重态的一项重要特征为其Ts较长,而且通常长于T1.不断改变三种单重态制备序列中cw去耦脉冲时间t(范围均为1~80 s),可以采集到一系列核自旋单重态的NMR谱图,对二自旋体系Hc、Hc'的相应信号进行积分并进行归一化处理,最终可以得到使用每种脉冲序列制备得到的核自旋单重态的Ts.SLIC序列中自旋锁定部分的时间为131 ms,功率为49.5 dB;cw去耦脉冲的功率为35 dB.M2S序列中M2S模块部分的时间
利用SLIC脉冲序列制备的Hc、Hc'核自旋单重态的Ts衰减曲线如图 8(b)所示.黑点为改变SLIC脉冲序列中的cw去耦时间t时,自旋体系Hc、Hc'对应的归一化积分面积,实线为使用公式y=A*exp(-x/Ts)拟合得到的曲线,拟合得到利用SLIC脉冲序列制备的核自旋单重态Hc、Hc'的Ts为(17.56±0.40)s,是T1的20.28倍.同样,利用M2S脉冲序列制备的Hc、Hc'核自旋单重态的Ts衰减曲线如图 8(c)所示,拟合得到Ts为(18.31±0.21)s,是T1的21.14倍.利用OC脉冲序列制备的Hc、Hc'核自旋单重态的Ts衰减曲线如图 8(d)所示,拟合得到Ts为(17.24±0.26)s,是T1的19.91倍.
由以上实验结果可知,我们通过三种不同方法获得的二自旋体系Hc、Hc'的单重态的Ts均明显长于其T1,且差异不大,这与单重态弛豫的基本原理一致.单重态的弛豫过程是分子的内禀属性,与分子自身的性质和所处的化学环境有关,对于AGG分子的目标自旋体系Hc、Hc'来说,理论上转变为的目标态均为
3.3 讨论
上述一系列实验结果证明,使用3种脉冲序列都可以成功实现对同一自旋体系核自旋单重态的有效制备;而且最终获得的单重态的Ts几乎没有差别,且均明显大于其T1.采用SLIC、M2S和OC脉冲获得的单重态的Ts分别为17.56 s、18.31 s和17.24 s,分别为其T1的20.28、21.14和19.91倍,符合单重态的基本弛豫规律.使用3种脉冲序列获得的单重态的Ts存在微小差异,可能与实验过程引起的误差有关.
但是,采用不同脉冲序列获得单重态的制备效率出现比较明显的差异.在我们使用的3种脉冲序列中,通过OC脉冲获得AGG分子中Hc、Hc'单重态的实验制备效率最高,能够达到43.3%;其次为SLIC脉冲,约为39.5%,而M2S脉冲实验制备效率最低,仅为17.2%.
除考虑了单重态转化为单量子态后会引起最终检测时的效率变化外,由于AGG分子的T1较短,与分子本身的弛豫时间相比,实验所用的三种脉冲序列的脉冲时间相对较长,因而脉冲施加期间自旋的弛豫因素不可忽略.如果考虑脉冲期间弛豫的影响,脉冲序列的理论制备效率还会有所下降.SLIC、M2S和OC脉冲观测信号强度衰减分别为0.739、0.594和0.602,最终计算获得的SLIC、M2S和OC脉冲最高理论制备效率分别约为38.9%、40.8%和65.3%.另外,原子核自旋单重态的J耦合值是单重态制备中所必需的重要参数,该值的测量精确度会明显影响单重态制备的效率.在我们的实际研究体系中,AGG分子内二自旋体系Hc、Hc'是一组强耦合体系,而强耦合体系由于存在roof效应,会导致体系内相关原子核自旋J耦合值的准确测量比较困难.此外在实验操作中,90°硬脉冲的功率是否完全准确,射频中心是否精准,梯度场能否把非单重态信号完全散相,制备过程中可能还存在一些双量子信号等,以上这些因素的综合影响下,导致了实验制备效率与理论制备效率的差异.
此外,引起不同脉冲制备单重态效率差异的来源除了三组脉冲序列对体系哈密顿量的演化不同外,还与脉冲的复杂度有关.OC脉冲因为脉冲的可变量比传统脉冲多,理论上能够实现状态的最大转移,但因为脉冲片段较多,实验中会因为单个小脉冲的不准确而累计产生较大的误差;SLIC脉冲具有强选择性,脉冲本身覆盖的范围较小,实现起来更加简单并且高效;而M2S脉冲覆盖范围较宽,其中的90°和180°脉冲的不准确或者当中的延时有误差时会引起效率显著下降.
4 结论
本文以AGG分子中一组二自旋体系的1H核为研究对象,利用三种脉冲序列均成功制备了该自旋体系的单重态;并通过实验测定比较了采用不同脉冲序列所获得单重态的制备效率和Ts.在脉冲序列的模拟计算中,由于自旋体系中的哈密顿量的演化在不同脉冲序列的作用下会出现差异,会导致不同脉冲序列理论计算的单重态制备效率不同.而在实际实验操作中,同一方法获得的单重态制备效率一般会低于相应的理论计算值,这一差异取决于实验过程中相关参数测定、仪器精度、弛豫影响、后期实验数据处理等多种因素.我们的实验结果还证明,采用不同单重态制备脉冲序列获得的同一体系内原子核自旋单重态的Ts基本一致,且明显长于T1,而不同脉冲制备的AGG分子的单重态制备效率相对差异较大.这一系列结果有助于我们更好地了解自旋体系的相关弛豫机制;在核自旋单重态的开发利用中,正确认识单重态制备脉冲序列这一影响因素,对于核自旋单重态在磁共振领域的实际应用具有积极重要的参考意义.
参考文献
Selective preservation and origin of petroleum-forming aquatic kerogen
[J].DOI:10.1038/305498a0 [本文引用: 1]
31P NMR spectroscopy in food analysis
[J].DOI:10.1016/j.pnmrs.2008.09.002 [本文引用: 1]
High-resolution pure shift NMR spectroscopy offers better metabolite discrimination in food quality analysis
[J].DOI:10.1016/j.foodres.2019.108574 [本文引用: 1]
Quantification of drugs encapsulated in liposomes by 1H NMR
[J].DOI:10.1016/j.colsurfb.2019.03.039 [本文引用: 1]
Imaging brain microstructure with diffusion MRI: practicality and applications
[J].DOI:10.1002/nbm.3841 [本文引用: 1]
3-T high-b-value diffusion-weighted MR imaging of hyperacute ischemic stroke in the vertebrobasilar territory
[J].DOI:10.1016/j.neurad.2011.09.005 [本文引用: 1]
Temperature dependence of spin-spin and spin-lattice relaxation times of paramagnetic nitrogen defects in diamond
[J].DOI:10.1063/1.477511 [本文引用: 1]
Beyond the T1 Limit: singlet nuclear spin states in low magnetic fields
[J].
Preparation of nuclear spin singlet states using spin-lock induced crossing
[J].
Long-lived nuclear spin states far from magnetic equivalence
[J].DOI:10.1039/C4CP05704J [本文引用: 1]
Long-lived nuclear spin states in high-field solution NMR
[J].DOI:10.1021/ja0490931 [本文引用: 2]
A nuclear singlet lifetime of more than one hour in room-temperature solution
[J].DOI:10.1002/ange.201411978 [本文引用: 4]
Long-lived nuclear spin states in the solution NMR of four-spin systems
[J].DOI:10.1016/j.jmr.2006.06.034 [本文引用: 1]
The Long-lived nuclear singlet state of 15N-Nitrous oxide in solution
[J].DOI:10.1021/ja803601d [本文引用: 2]
J-Stabilization of singlet states in the solution NMR of multiple-spin systems
[J].DOI:10.1016/j.jmr.2007.03.019 [本文引用: 1]
Determination of molecular torsion angles using nuclear singlet relaxation
[J].DOI:10.1021/ja1012917 [本文引用: 1]
Real-space imaging of macroscopic diffusion and slow flow by singlet tagging MRI
[J].DOI:10.1016/j.jmr.2015.01.016 [本文引用: 1]
Relaxation editing using long-lived states and coherences for analysis of mixtures
[J].DOI:10.1021/acs.analchem.6b00050 [本文引用: 1]
Slow diffusion by singlet state NMR spectroscopy
[J].DOI:10.1021/ja052897b [本文引用: 1]
Recycling and imaging of nuclear singlet hyperpolarization
[J].DOI:10.1021/ja312333v [本文引用: 1]
Preparation of singlet states and analysis of influencing factors on their transfer efficiency and lifetime
[J].
核自旋单重态的制备及其转化效率和寿命的影响因素分析
[J].
Preparation of long-lived states in a multi-spin system by using an optimal control method
[J].DOI:10.1002/cphc.202000038 [本文引用: 5]
Robust conversion of singlet spin order in coupled spin-1/2 pairs by adiabatically ramped RF-fields
[J].DOI:10.1016/j.jmr.2016.10.003 [本文引用: 1]
Long-lived states in multiple-spin systems
[J].DOI:10.1002/cphc.200900335 [本文引用: 1]
Optimal control in NMR spectroscopy: Numerical implementation in SIMPSON
[J].DOI:10.1016/j.jmr.2008.11.020 [本文引用: 1]