引言
锥形束计算机断层扫描(Cone Beam Computed Tomography,CBCT)即锥形束CT,因具有扫描时间短、辐射剂量小、设备轻便等优点而被广泛应用于口腔诊断领域.通过对CBCT所得二维图像进行重建,实现牙齿及牙槽骨等骨性结构的三维显示,这将大大减少医生的诊断难度,同时为治疗方案的确定和虚拟手术的实现提供便利.但由于CBCT具有辐射性,磁共振成像(Magnetic Resonance Imaging,MRI)逐渐成为了更安全的口腔检测成像手段.因为成像原理的不同,牙齿及牙槽骨在CBCT图像中为高密度影像,而在MRI中为低密度影像,且由于MRI主要适用于软组织成像,骨性组织分辨率较差,因此虽能基本完整地展现牙齿与牙槽骨的形态与结构,但依然存在相邻牙齿间黏连、牙根处拓扑结构改变、牙齿与牙槽骨皮质连接处等复杂结构无法清晰分辨的问题.利用MRI检测下颌骨病,并将牙齿从图像分割出来后,可以对牙槽骨和下颌骨病变作出更准确地诊断.
把牙齿和牙槽骨分别从二维图像中分割出来,是实现骨性结构三维重建的基本前提;并且分割的精确度将直接影响重建的效果.因此,如何实现二维图像中牙齿及牙槽骨的精确分割就成为一个关键问题.水平集方法由Osher和Sethian[1]在1988年提出,因其在描述复杂拓扑结构上的独特优势,水平集方法近年来被广泛应用于图像识别、检测等领域.国内外研究人员对于改进水平集算法有过许多研究.Gao等[2]首次将基于边界、基于区域及基于先验形状约束能量项加入到水平集中,提出了一种混合的水平集模型.Zhang等[3]基于反应扩散正则化提出了一种新的水平集演化方法,佐以两步裂项法,可大大降低计算的复杂性.由于单一的能量模型很难准确分割目标,Wang等[4]提出了一种由多尺度局部似然图像拟合(Local Likelihood Image Fitting,LLIF)能量项、自适应先验形状约束能量项和反应扩散(Reaction Diffusion,RD)正则化能量项组成的混合水平集模型,能够有效提高分割精度.
Li等[5]于2010年提出一种避免初始化水平集函数的距离正则化水平集演化(Distance Regularized Level Set Evolution,DRLSE)模型,其通过加入距离正则项(Distance Regularized Term)使零水平集函数在向目标物体边缘移动的过程中,保持了其符号距离特性.但通过观察其距离正则项所对应的势阱函数,发现该势阱函数在水平集函数梯度
1 水平集模型
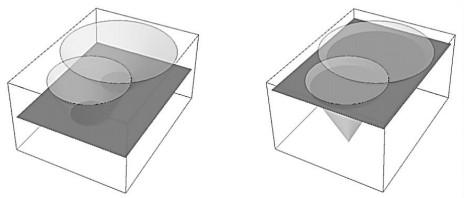
水平集方法能够简明地表示复杂拓扑结构的基础思想在于其将n维曲面的演化问题转化为n+1维空间中隐式方程解集合,即水平集的演化.因此二维曲线运动将转化为三维曲面运动,即该曲线每一个时刻的变化均可利用三维曲面的零水平面来表达.图 1为水平集方法示意图.
图1
但利用水平集进行曲线演化的缺点是要进行周期性初始化,为避免复杂的初始化过程,Li等[5]提出了归一化符号距离函数.通过在能量泛函中构造势阱函数决定的正则项来保证每一次演化后符号距离函数的值满足一定条件,从而避免了对水平集函数即该符号距离函数的重新初始化.水平集函数定义为:
其中,d为正常数,Ω表示初始轮廓区域.初始轮廓内部设定为负值,初始轮廓外部设定为正值.为驱动该水平集函数表示的曲线向着感兴趣区域的边界移动,定义水平集能量泛函
(2) 式第一项中,
其中P(·)为势阱函数,
(2) 式第二项中,
其中
边缘指示函数g用(6)式表示,其中
(2) 式第三项中,
其中g为边缘指示函数,
(2) 式中,
2 基于混合水平集模型的牙齿牙槽骨分割算法
2.1 DRLSE势阱函数
正则项的作用不仅是平滑水平集函数,更重要的一点是令至少在零水平集附近区域内满足
Li等[5]在DRLSE模型中采用了一种双势阱函数来保持水平集函数的符号距离特性即
其中,s表示水平集梯度
2.2 改进的双势阱函数
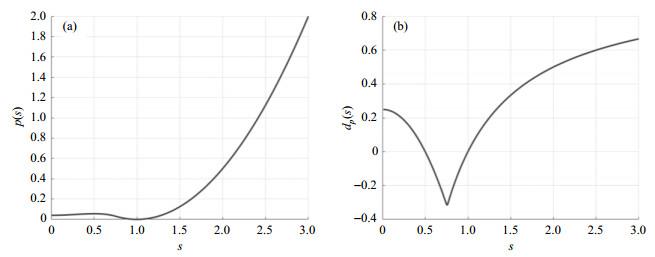
针对Li提出的双势阱的不足,孙超等[9]提出了V势阱函数,该函数统一了演化速度的数学表达形式,在避免零势阱修正的同时,降低了零势阱附近的演化速度.本文在双势阱的基础上提出了一种新的势阱函数—单勾势阱函数.势阱函数
如图 2(a)所示,本文的势阱函数同属于双势阱函数,由零势阱和壹势阱构成.扩散速率函数为水平集梯度
图2
图2
单勾势阱函数图.(a)势阱函数;(b)扩散速率函数
Fig.2
Diagram of single hook well function. (a) Potential well function; (b) Diffusion rate function
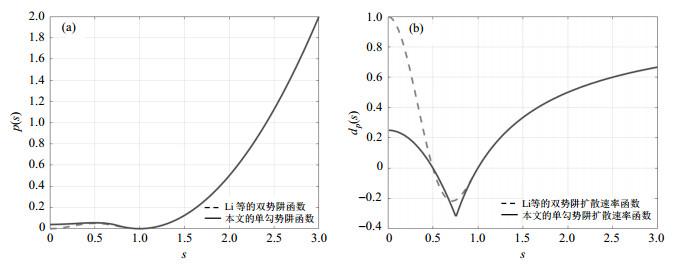
与Li等提出的DRLSE模型中的双势阱函数相比,本文提出的单勾势阱函数有如下优势:(1)扩散速率函数在
图3
图3
单勾势阱函数与Li等提出的双势阱函数对比图.(a)势阱函数对比;(b)扩散速率函数对比
Fig.3
Comparison of single hook well function and double well function proposed by Li et al. (a) Comparison of potential well function; (b) Comparison of diffusion rate function
在以往的水平集模型中,为了抑制由噪声引起的非均匀性,常常使用大尺度高斯滤波对图像进行预处理[10].而图像中的纹理变化常常是非均匀性的,恒定方差的高斯滤波不能平滑图像区域的非均匀性.若方差较大,对应的高斯滤波器模板尺度也较大,图像边缘损失较多,容易导致目标区域出现过分割;反之,若方差较小,高斯滤波器模板尺度较小,图像非均匀性程度过大,容易导致目标区域出现欠分割[10].另外,DRLSE模型是基于边缘的分割方法,此类方法的主要缺点有:(1)初始轮廓会影响分割的精确度;(2)对图像噪声很敏感;(3)在弱边缘情况下演化结果不好[11].而边缘指示函数g依赖光滑图像的梯度,所以在分割含噪图像时,演化曲线受噪声干扰容易陷入虚假边缘[12].因此,当目标之间的距离很近时,此时若使用大高斯核滤波,会使边界处的灰度值被其邻域的加权灰度值取代,而其邻域中像素多为目标像素,故原先低灰度边界灰度上升,到一定程度后,边界消失,目标边界可能相互连接,导致分割失败[13].
为了得到较好的分割效果,将序贯滤波应用于本文的水平集模型,利用小方差高斯滤波的优势,对图像进行多次小方差滤波的叠加,平滑过程可抽象为:
其中,
(14) 式表明,两次高斯函数方差
为避免水平集迭代次数过多导致目标区域过度平滑失去边缘特征而出现曲线侵入,文献[10]提出用区域置信度作为判定的标准之一,根据不同等效方差的高斯函数分割结果的区域置信度决定序贯滤波次数,其区域置信度Pr定义为:
其中,
在以往的研究中,对于同一患者的不同牙齿多采用相同尺寸的牙盒作为初始轮廓,这样虽然在选取时较为方便,但却是以增加水平集迭代次数、增加数据提取时间作为代价的.本文将针对不同牙齿的特点,设置不同尺寸、不同迭代次数,以提高分割效率.为了进一步利用相邻序列图片中同一结构的相似性,本文将先验信息[14]加入对下层图像的分割中,以当前层对单一牙齿的分割结果作为下层图像中同一牙齿的初始轮廓,以求在相对少的迭代次数下得到准确的结果.考虑到牙齿的部分图像会出现当前层轮廓小于下层轮廓的现象,故在定义下层初始轮廓时先对当前层最终轮廓做形态学膨胀处理,以避免出现曲线侵入而使得结果不准确.
2.3 基于阈值法和孔洞填充的牙槽骨分割
图4
2.4 牙齿牙槽骨分割算法步骤
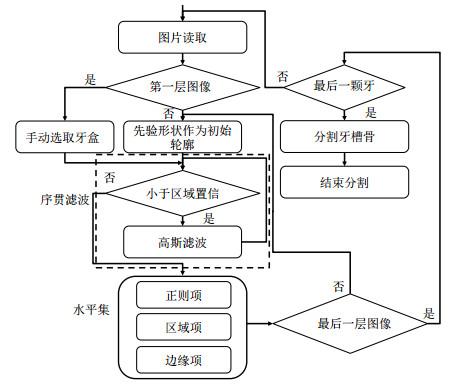
牙齿牙槽骨分割算法步骤如图 5所示,具体步骤如下:
图5
图5
本文提出的牙齿牙槽骨图像分割算法的流程图
Fig.5
Algorithm flow chart for segmentation of tooth and alveolar bone proposed in this research
Step1. 参数初始化:设定步长、正则项系数
Step2. 读取DICOM图像,对其进行灰度均一化处理和对比度增强
Step3. 牙齿分割
a. 水平集初始化,对第一层图像手动取框作为初始水平集曲线
b. 在区域置信度内进行小尺度高斯滤波,并计算图像梯度,生成边缘停止函数
c. 计算单勾势阱函数演化速度
d. 计算水平集能量项最小化迭代公式,使其驱使轮廓线停止在牙齿边缘处得到分割结果
e. 读取下一层图像,对上一层的分割结果小尺度膨胀后作为下一层的初始水平集曲线
f. 重复步骤b~e,直到分割完全部图层,完成此颗牙齿的序列分割
g. 重复步骤a~f,进行下一颗牙齿的分割,直到完成所有牙齿的序列分割
Step4. 牙槽骨分割
a. 通过阈值法对牙槽骨进行分割,并对孔洞进行填充
b. 读取下一层图像
c. 重复步骤a~c,直到分割完全部图层,完成牙槽骨分割
3 实验结果
本文实验数据为10组CBCT口腔图像以及3组口腔磁共振图像,采集于上海市第九人民医院,其中CBCT扫描电压为90 kV,曝光时间为10.8 s,获得数据矩阵大小为595×595×358,像素分辨率为0.25×0.25×0.25 mm3;MRI扫描序列为T1W_TSE,TR为507 ms,层厚为4 mm,图片尺寸为336×336.图像的数据类型为16位无符号整型,保存的格式为DICOM文件.
本文的实验环境为:CPU处理器为Inter(R) Core(TM) i5 CPU(2.30GHz),内存8.0GB,MATLAB R2016b软件下编写程序完成实验,实验参数为
3.1 牙齿分割效果
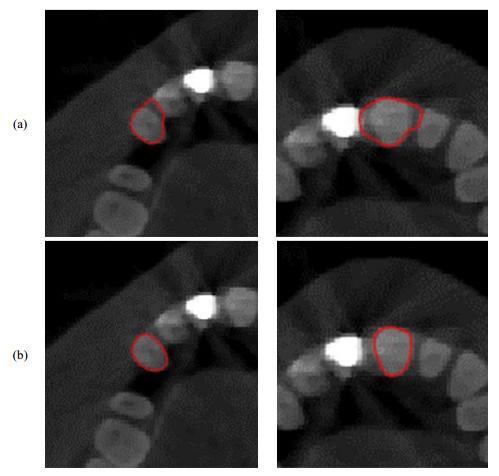
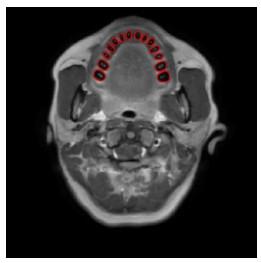
将16位数据转换为8位的灰度图像,手动画取合适大小的相同初始框,并选择相同的实验参数后,分别采用DRLSE模型和本文提出的水平集模型对CBCT图像及磁共振图像中的牙齿进行分割.图 6为CBCT图像分割结果,可以发现Li等的方法可能会把相邻牙齿的轮廓错分为目标牙齿的轮廓,导致欠分割.而本文提出的算法模型在相邻牙齿相互粘连、牙齿和牙槽骨灰度值相近的情况下,能够驱使水平集函数表示的曲线到达目标牙齿的边界处,而不会停留在相邻牙齿和牙槽骨的分界处.由此可见,本文的算法对牙齿有精确的分割能力,可以很好地改善DRLSE模型的欠分割的情况.图 7为文本算法运用于磁共振图像的实验结果,亦可准确有效地分割出磁共振图像中的单颗牙齿.
图6
图6
基于CBCT图像的(a) DRLSE模型牙齿分割结果和(b)本文模型牙齿分割结果
Fig.6
Tooth segmentation with (a) DRLSE model, and (b) the proposed model in this research based on CBCT images
图7
图7
基于磁共振图像的本文模型牙齿分割结果
Fig.7
Tooth segmentation with the proposed model in this research based on magnetic resonance image
本文从分割的精确性及运算时间两个角度来评价算法的优劣.采用积重叠误差(Volumetric Overlap Error,VOE)[17]来进行基于区域的精确性描述,VOE定义如下:
其中A为算法自动分割的结果,B为手动勾画结果并作为标准.通过计算水平集分割算法和手动分割结果的交集和并集的体积比得到的就是两者的真实重叠度,VOE越小,说明分割的结果与标准的重叠度越高,即分割结果越准确.基于CBCT图像,本文算法与DRLSE分割结果的定量比较如表 1所示,可见本文算法在分割精确度上相比DRLSE有明显的提升,算法效率上也有一些提高,但由于序贯滤波增加了算法的时间,因此该优势并不明显.
表1 基于CBCT图像,本文算法与DRLSE模型进行牙齿分割结果的定量比较
Table 1
| 组别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 平均值 | 标准差 | |
| 本文算法 | VOE/% | 8.84 | 8.36 | 9.42 | 8.41 | 8.77 | 8.01 | 6.13 | 10.32 | 9.57 | 8.23 | 8.61 | 1.06 |
| 运算时间/s | 15.32 | 15.04 | 14.33 | 14.34 | 15.30 | 14.68 | 15.92 | 14.88 | 14.23 | 14.28 | 14.83 | 0.54 | |
| DRLSE | VOE/% | 16.02 | 16.88 | 18.32 | 15.60 | 9.66 | 15.50 | 8.73 | 18.23 | 16.53 | 13.77 | 14.92 | 3.13 |
| 运算时间/s | 16.65 | 16.23 | 15.99 | 16.77 | 15.34 | 14.67 | 15.66 | 17.33 | 18.19 | 14.83 | 16.16 | 1.05 |
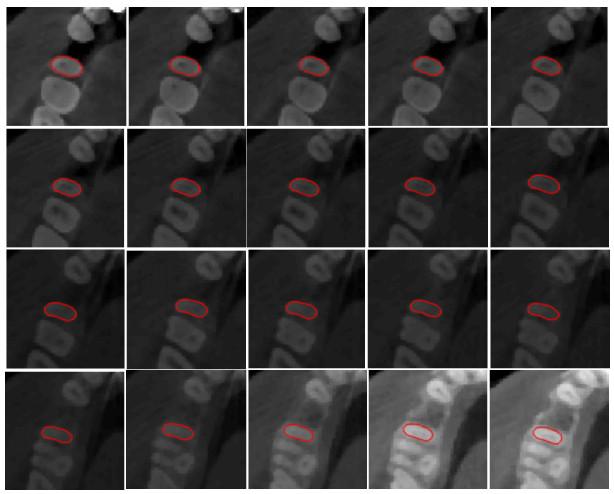
利用本文提出的水平集算法对同一样本中同一颗牙齿的CBCT多层序列图像进行分割,结果如图 8所示.对第一层图像进行手动画框后,即可通过本文的水平集算法对目标牙齿进行准确的分割,将此层分割结果曲线进行小尺度膨胀后作为下一层的水平集初始轮廓,即可无中断地进行序列图像的牙齿分割,避免了重复初始化.实验结果表明,利用本文的方法能过对CBCT序列图像完成准确的牙齿分割,基本不会出现欠分割或是过分割的情况.
图8
3.2 牙槽骨分割效果
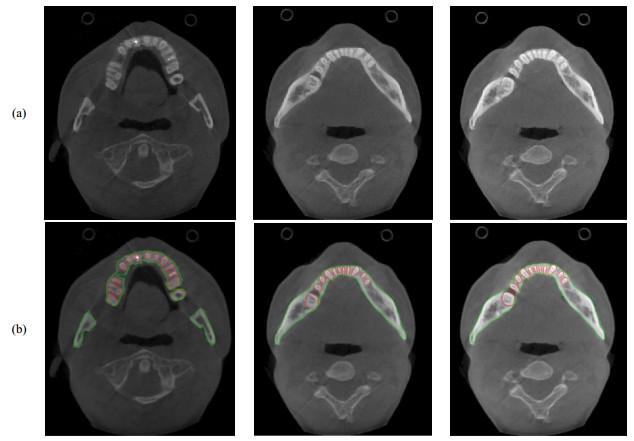
图9
图9
(a) CBCT原图;(b)使用本文算法的牙槽骨分割结果
Fig.9
(a) Original CBCT image; (b) Segmentation results of alveolar bone using the algorithm proposed in this research
图10
4 结论
本文针对CBCT及磁共振图像中牙齿的特点,对以往水平集模型中不适合应用于此类图像的部分做出了改进,并将其应用在牙齿CBCT及磁共振图像分割中,得到了更为准确的分割结果.其中创新的单钩势阱函数克服了现有势阱函数使用限制多、弱边缘难以检测等缺点;将序贯滤波与水平集模型结合改善了原有水平集模型中单次使用大尺度高斯核而使图像信息丢失的情况;根据断层序列图像特点,将当前层分割结果作为下层图像初始框,实现先验信息的充分利用.
无
参考文献
Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations
[J].DOI:10.1016/0021-9991(88)90002-2 [本文引用: 1]
Individual tooth segmentation from CT images using level set method with shape and intensity prior
[J].
Active contours driven by local image fitting energy
[J].DOI:10.1016/j.patcog.2009.10.010 [本文引用: 1]
Accurate tooth segmentation with improved hybrid active contour model
[J].DOI:10.1088/1361-6560/aaf441 [本文引用: 1]
Distance regularized level set evolution and its application to image segmentation
[J].DOI:10.1109/TIP.2010.2069690 [本文引用: 4]
Development of teeth segmentation from computed tomography images using level set method
[J].DOI:10.3969/j.issn.1001-3695.2016.03.042 [本文引用: 1]
基于水平集的牙齿CT图像分割技术
[J].DOI:10.3969/j.issn.1001-3695.2016.03.042 [本文引用: 1]
Individual tooth segmentation from CT images using level set method with shape and intensity prior
[J].DOI:10.1016/j.patcog.2010.01.010 [本文引用: 1]
Ultrasound image segmentation of thyroid gland based on bilateral filters-distance regularized level
[J].
基于双边滤波-距离正则化水平集演化算法的甲状腺超声图像分割
[J].
Distance regularised level set method using v-potential well function
[J].DOI:10.3969/j.issn.1000-386x.2013.04.078 [本文引用: 1]
采用V势阱函数的距离归一化水平集算法
[J].DOI:10.3969/j.issn.1000-386x.2013.04.078 [本文引用: 1]
The level set image segmentation on sequential filtering
[J].
基于序贯滤波的水平集图像分割
[J].
Image segmentation by level set evolution with region consistency constraint
[J].DOI:10.1007/s11766-017-3534-0 [本文引用: 1]
An improved method for image segmentation based on DRLSE level set
[J].
基于改进DRLSE水平集模型的图像分割
[J].
Active contour model based on adaptive sign function
[J].
基于自适应符号函数的主动轮廓模型
[J].
Using prior shapes in geometric active contours in a variational framework
[J].DOI:10.1023/A:1020878408985 [本文引用: 1]
A survey ofthresholding techniques
[J].DOI:10.1016/0734-189X(88)90022-9 [本文引用: 1]
Fast and robust segmentation of individual tooth crown from cone beam computed tomography images
[J].
Comparison and evaluation of methods for liver segmentation from CT datasets
[J].DOI:10.1109/TMI.2009.2013851 [本文引用: 1]